環氧瀝青鋪裝對鋼橋面板受力影響試驗研究

王石磊，齊法琳，柯在田，高 巖

(中國鐵道科學研究院集團有限公司基礎設施檢測研究所，北京 100081)

正交異性鋼橋面板(以下簡稱“鋼橋面板”)具有自重輕、整體剛度大、施工速度快的特點，是大跨度橋梁最常使用的橋面形式[1]。為確保車輛行駛的舒適性和減少車行荷載對鋼橋面的沖擊，通常在鋼橋面板上設置鋪裝層，我國鋼橋面板常用鋪裝形式有改性瀝青SMA、澆注式瀝青混凝土和環氧瀝青混凝土三種方案[2]。隨著鋼橋面板的廣泛使用和服役時間的逐漸增加，該類結構產生了不同程度的疲勞裂紋[3]。研究表明改進鋪裝層結構或確保鋪裝的完整性，可以減小鋼橋面板關鍵部位的受力，進而延緩鋼橋面板疲勞敏感部位的使用壽命[4?7]。

國內某懸索橋鋼箱梁竣工時橋面鋪裝采用改性瀝青SMA 方案，通車運行數年后原有鋪裝頻繁出現推移、車轍、開裂的現象，鋼橋面板U 肋與面板連接部位、U 肋與橫隔板連接部位、U 肋嵌補段出現了大量的疲勞裂紋，管養部門針對鋼橋面板疲勞開裂開展了專項的維修加固處理，同時將原鋪裝更換為強度高、耐腐蝕性及疲勞性能好的環氧瀝青混凝土鋪裝[8]。為考察環氧鋪裝對鋼橋面板關鍵部位受力改善效果及穩定性能，筆者開展了長達6 年的實橋試驗研究，以期為同類工程應用及鋼橋面板病害處治提供參考和借鑒。

1 背景橋梁概況

1.1 鋼橋面板結構簡介

本文背景橋梁為懸索橋，加勁主梁采用扁平閉合流線型鋼箱梁，橋面寬度為35.6 m，按雙向六車道設計，吊索縱向間距12 m，橋面系采用鋼橋面板結構，橋面板厚12 mm，閉口U 肋規格為320 mm×260 mm ×8 mm，橫向間距620 mm。橫隔板板厚8 mm，縱橋向間距4 m。鋼橋面板細部構造如圖1 所示。

1.2 鋼橋面板病害

背景橋梁鋼橋面板主要存在以下4 種類型病害，分布示意如圖2 所示。

1) 部位1：U 肋與面板連接焊縫位置處裂紋，裂紋豎向貫穿面板；

2) 部位2：U 肋與橫隔板連接部位弧形切口處裂紋，裂紋沿橫隔板母材斜向發展；

3) 部位3：U 肋與橫隔板連接豎向焊縫下端部裂紋，裂紋沿橫隔板母材斜向發展；

4) 部位4：U 肋嵌補段現場焊縫位置處裂紋。

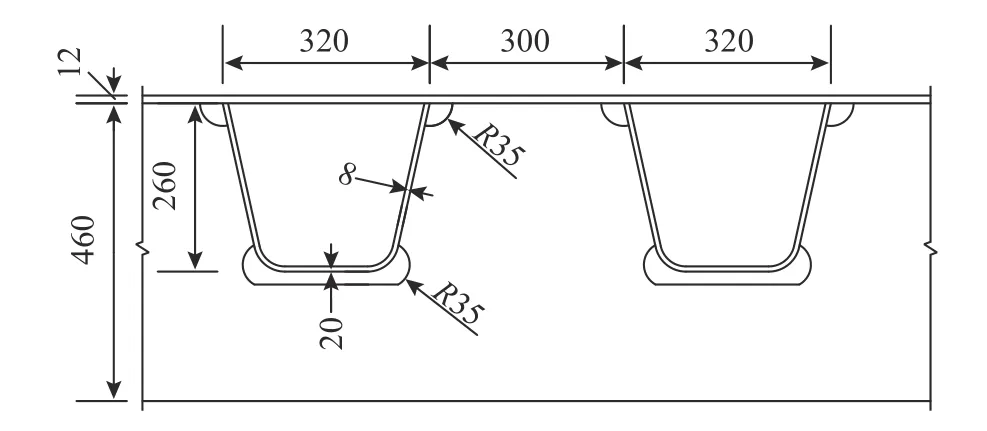
圖1 鋼橋面板細部構造 /mm Fig.1 Configuration of steel orthotropic deck

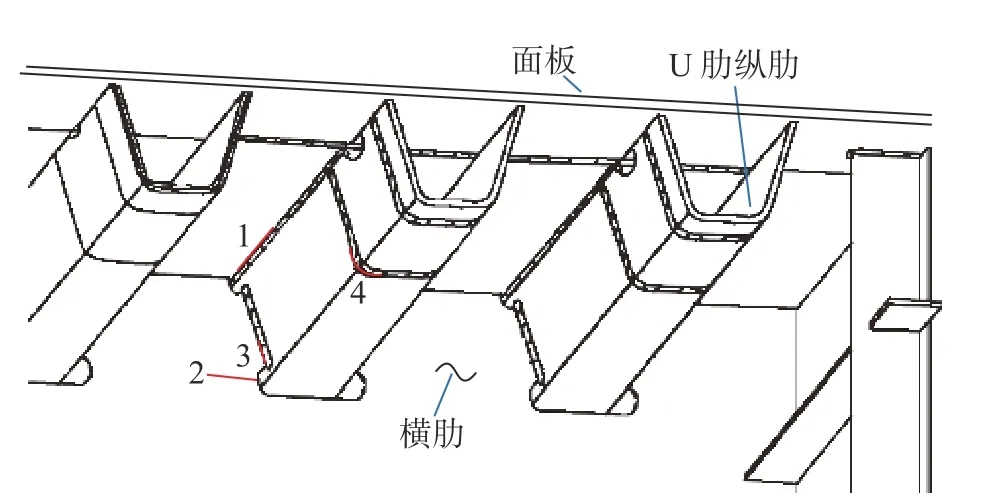
圖2 背景橋梁鋼橋面板病害分布Fig.2 Fatigue crack layout of orthotropic steel deck

1.3 環氧瀝青混凝土鋪裝

鋪裝設計厚度70 mm，結構組成為：35 mm環氧瀝青混凝土(EA10)+粘結層+35 mm 環氧瀝青混凝土(EA10)+防水粘結層，結構如圖3 所示。

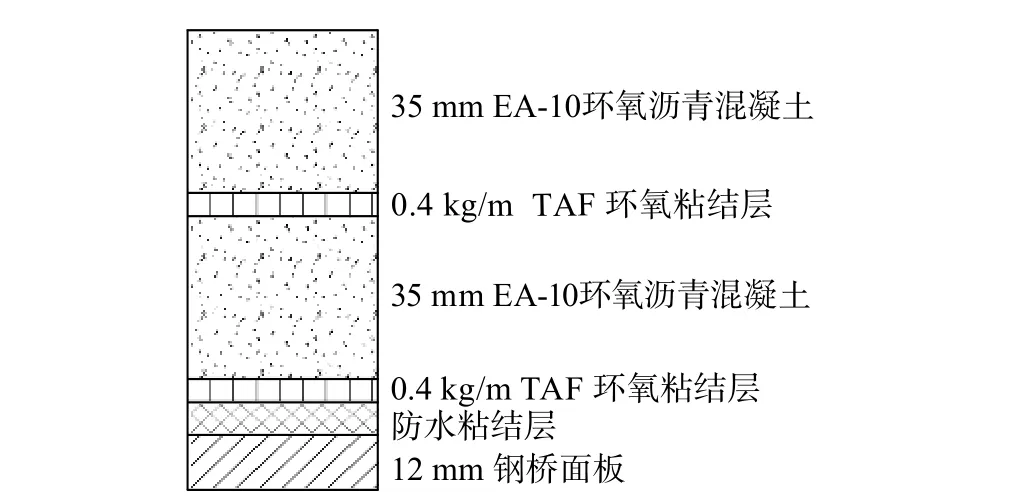
圖3 環氧瀝青混凝土鋪裝方案Fig.3 Structure of epoxy asphalt concrete pavement

2 試驗方案

為分析環氧瀝青混凝土鋪裝對鋼橋面板局部應力和變形的改善效果，在不同鋪裝狀態(原鋪裝、鋪裝鏟除后、新鋪裝)及不同環境(低溫、高溫)下開展現場試驗，并基于新鋪裝的材料特征建立了有限元仿真計算模型，對比實測與理論計算結果，研究測試部位受力特點和規律。

2.1 有限元仿真模型

有限元模型忽略第一體系的影響，模型橫橋向寬6200 mm，包含10 道U 肋，為橫向測試區域的5 倍，縱橋向長16000 mm，覆蓋4 道橫肋間距，為縱向測試區域8 倍，測試區域、模型計算區域、半幅鋼箱梁斷面布置如圖4 所示。采用ABAQUS建立鋼橋面板計算模型，單元采用C3D8R 型8 節點縮減積分實體單元，對試驗重點關注部位進行了單元細分，網格尺寸按應變計敏感柵長進行控制，部位1 單元尺寸約為2 mm，部位2 單元、3 單元尺寸約為3 mm，部位4 單元尺寸約為5 mm。模型邊界條件按四邊簡支考慮，約束橋面板及橫肋四周對應節點的x、y、z方向位移。橋面鋪裝與鋼板間采用界面耦合進行約束，不考慮材料非線性及界面滑移的影響。有限元模型如圖5 所示。環氧瀝青混凝土彈性模量與溫度相關，結合背景橋梁當地平均溫度，確定鋪裝層的彈性模量為3000 MPa，泊松比為0.25[9?10]；鋼材彈性模量為210 GPa，泊松比為0.3。

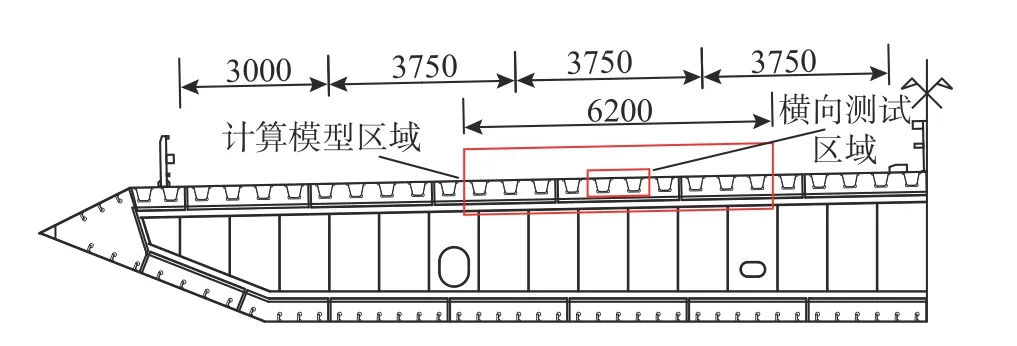
圖4 測試及計算區域橫橋向布置 /mm Fig.4 Transverse layout of test and calculation area

圖5 有限元模型Fig.5 Finite element model

2.2 測點布置

背景橋梁鋼橋面板4 種類型病害空間分布零散，測試區域選擇前進行了現場調查，保證測試區域前后2 道橫肋及橫向6 道U 肋(1 個車道)范圍內均未出現疲勞裂紋，以避免病害影響測試結果、有利于實測與有限元計算結果比較。

試驗選擇縱肋與面板連接部位、縱肋與橫隔板連接部位進行局部應力測試，縱向設置了A-A、B-B、C-C 三道測試斷面。A-A 測試斷面兼做鋼橋面板變形測試斷面。測點布局如圖6 所示。

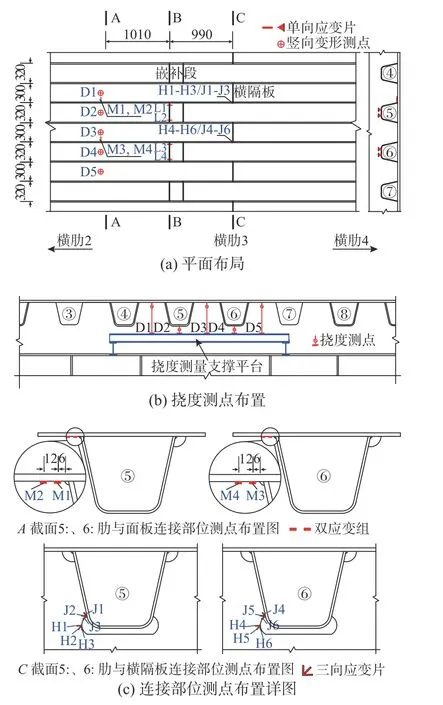
圖6 試驗測點布局 /mm Fig.6 Distribution of testing points

鋼結構應力選用中航電測電阻應變計測量，其中U 肋嵌補段縱向應力選用敏感柵長5 mm 的BE120-5AA 型單向應變計，橫隔板處局部應力選用45°夾角敏感柵長3 mm 的BE120-3CA 型三向應變計，U 肋與面板連接部位局部應力參考熱點應力法[11]選用敏感柵長2 mm 的BE120-2GD 型雙組應變計。每次試驗前均對各應變計防護及絕緣狀況進行檢查，確保測試結果的可靠，圖6 中所示測點為經驗證和分析在6 年周期內均穩定的測點，其他過程中受到破壞或絕緣狀況不佳的測點未含在本文之列。鋼橋面板變形采用千分表測量。部分測點安裝狀況如圖7 所示。

2.3 試驗加載

圖7 測點現狀安裝狀況Fig.7 Installation condition of measuring points

試驗加載采用雙軸貨車，加載重量充分考慮超載車輛的影響，前軸重為90 kN，后軸重320 kN(加載輪)。加載車軸距及車輪觸地面積布局如圖8(a)所示，基于影響面的思路進行計算和加載，橫橋向設置37 條加載線，如圖8(b)之T1～T37，縱橋向設置15 個加載輪位，如圖8(c)之L1～L15，受試驗時間限制，結合加載位置與測試部位的關系，選取典型計算工況進行實橋加載?，F場試驗組織狀況如圖9 所示。

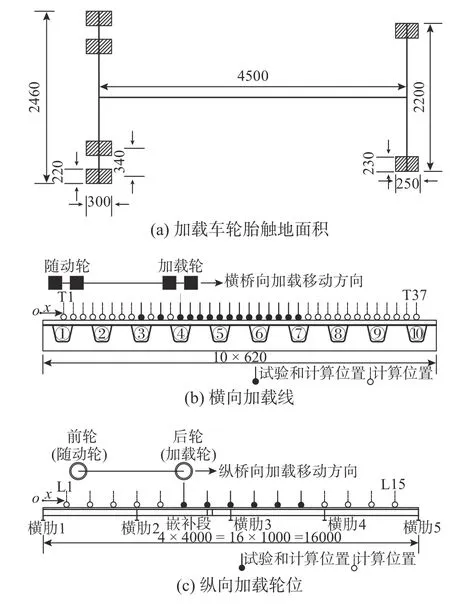
圖8 試驗加載控制 /mm Fig.8 Loading procedures

圖9 現場試驗照片Fig.9 Field test photos

2.4 試驗工況

實橋試驗共計進行了7 次，時間跨度為6 年。試驗工況安排見表1。

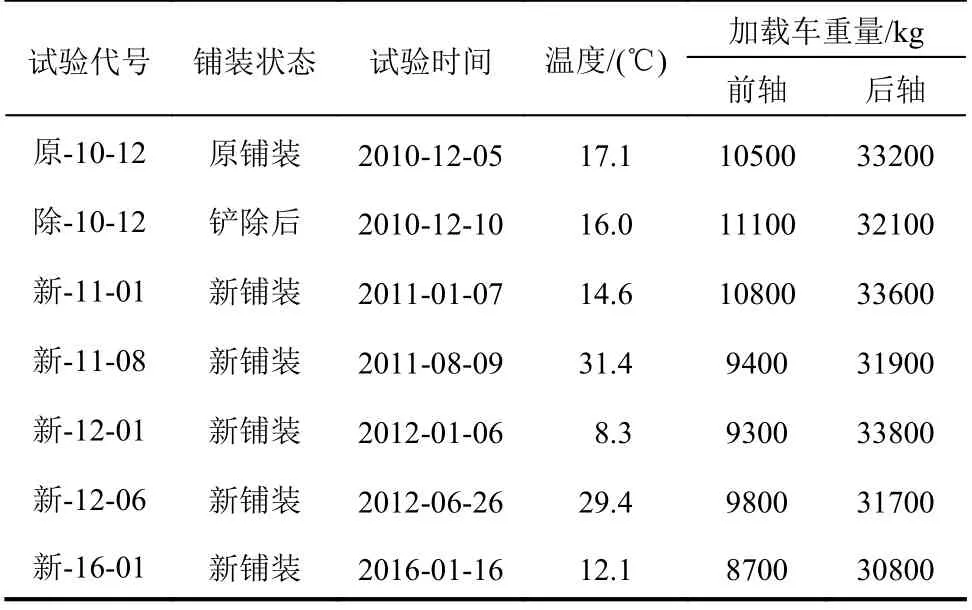
表1 試驗工況安排Table 1 Arrangement of field test

為減少環境對試驗結果的影響，試驗均在凌晨0:00～3:00 時間段及交通封閉條件下開展。歷次試驗確保測點位置、加載車輛及點位的統一。試驗數據按實際車輛后軸重與計算軸重320 kN 的比值進行線性換算后再進行對比分析。

3 試驗分析

3.1 U 肋與面板連接部位受力分析

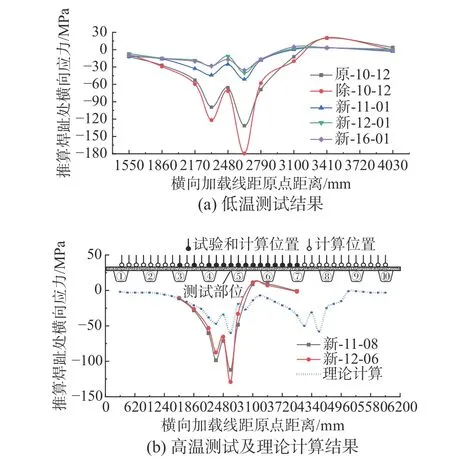
圖10 M1、M2 測點推算焊趾處應力結果Fig.10 Calculated stress of weld toe by M1&M2

U 肋與面板連接部位(部位1)典型測點應力與橫向加載線的關系如圖10 所示，試驗加載輪位作用下應力實測與理論計算變化規律一致，試驗荷載控制輪中心位于測試部位正上方時應力達到峰值，測試部位受加載線橫向位置影響較大，橫向影響區域約為2 道U 肋中心距(640 mm)，由于控制輪雙胎影響，同一橫向影響區內，應力存在雙峰的現象，因考慮了左、右側輪同時加載，未試驗加載的計算輪位與試驗輪位作用下的應力變化規律存在重演現象。相對于無鋪裝狀態，鋪裝對測試部位應力均存在改善，新鋪裝狀態下測試部位受力與溫度有強關聯性。

3.2 U 肋與橫隔板連接處受力分析

對平面應力狀態下的45°應變花測點，按照式(1)算出最大主應力、剪應力[12]。

式中：E為鋼材彈性模量；σ1為主拉應力；σ2為主壓應力；τmax為剪應力；μ為鋼材泊松比；ε0、ε45、ε90為三向應變測試結果。

橫隔板弧形切口處(部位2)及橫隔板與U 肋連接豎向焊縫下端(部位3)典型測點主拉應力與橫向加載線關系如圖11 所示。當荷載沿測試橫肋橫橋向移動時，計算及實測結果均表明當試驗荷載控制輪中心作用于測試部位正上方時該部位主拉應力較小，遠離該部位一個縱肋間距后主拉應力達到峰值，主拉應力實測與理論計算變化規律相近，計算主拉應力橫向影響范圍為2 道U 肋間距(1240 mm)，存在不同的是理論計算的主拉應力橫向梯度更大，即主拉應力實測橫向影響范圍大于理論計算結果，實際結構受力更為不利，因單元網格尺寸已按照應變計敏感柵長進行精細化設置，網格劃分影響可以忽略，實測與理論計算的偏差體現了鋼橋面板連接部位局部受力行為的復雜性和仿真計算的有限性。

部位2 及部位3 典型測點主拉應力與縱向加載輪位關系如圖12 所示。當荷載沿縱橋向移動時，計算及實測結果均表明當試驗荷載控制輪中心作用于測試部位對應橫肋時主拉應力達到峰值，說明測試部位以承受橫隔板面內受力為主，主拉應力實測與理論計算變化規律一致，計算測試部位主拉應力縱向影響范圍為2 道橫肋間距(8000 mm)。

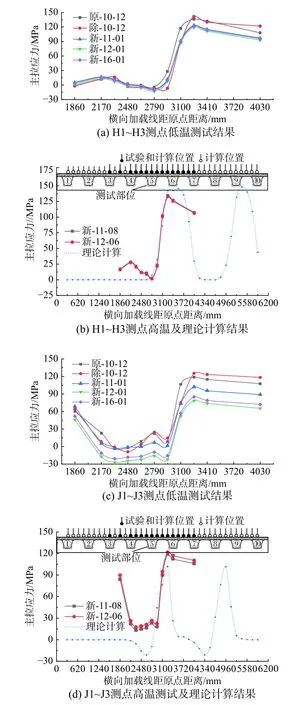
圖11 典型測點主拉應力與橫向加載位置關系Fig.11 Principal tensile stress with transverse loading line

相對無鋪裝狀態，鋪裝對測試部位應力均存在一定改善，新鋪裝狀態下，測試部位受力與高低溫環境有弱關聯性。

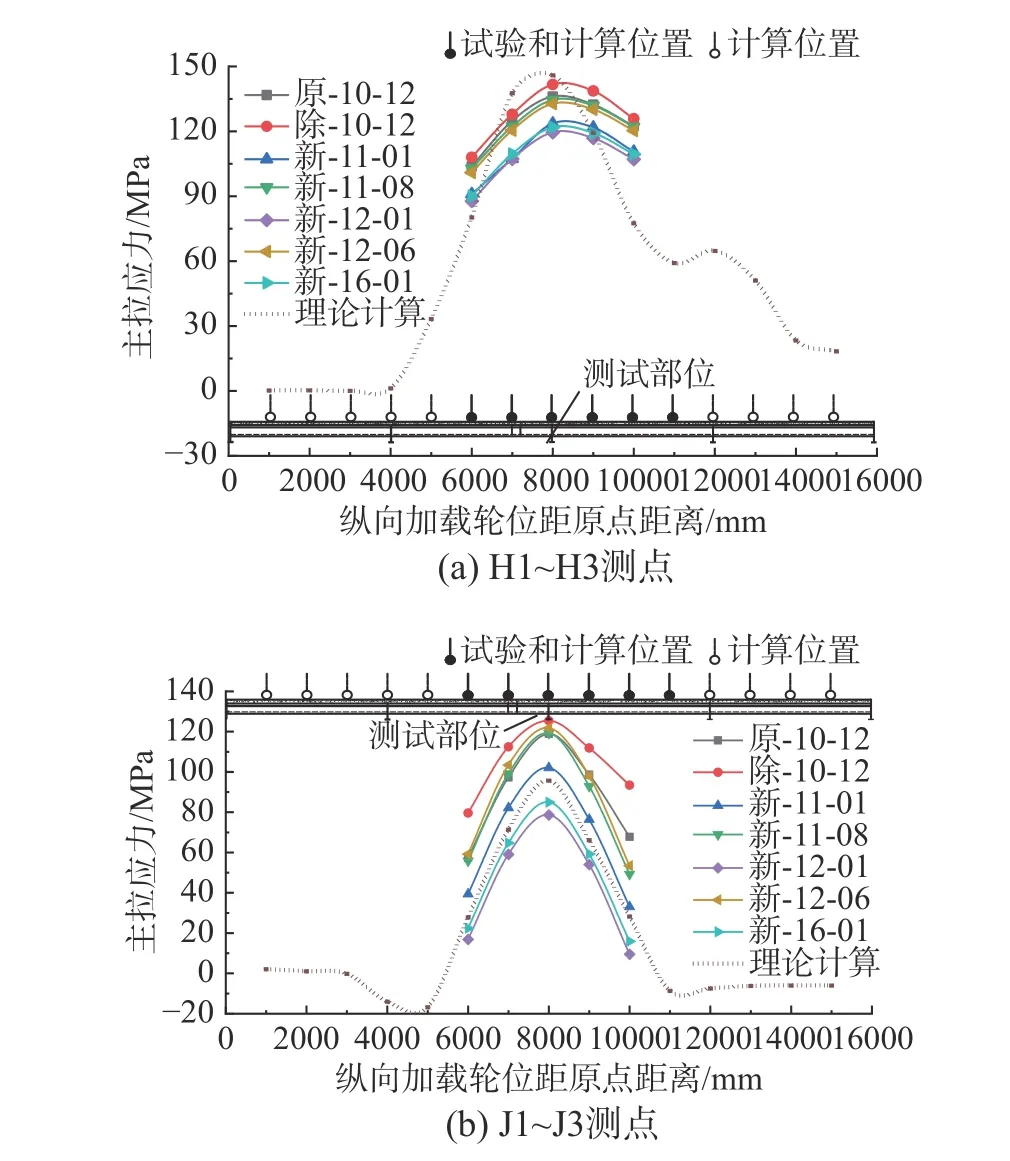
圖12 典型測點主拉應力與縱向加載輪位關系Fig.12 Principal tensile stress with longitudinal loading wheel position

3.3 U 肋嵌補段受力分析

U 肋嵌補段(部位4)典型測點應力與橫向加載線的關系如圖13 所示。試驗加載輪位作用下測試部位應力實測與理論計算變化規律一致，應力橫向影響區域約為4 道U 肋間距(2480 mm)。當試驗荷載控制輪中心位于測點所處的縱肋頂部時受力最為不利，因考慮了左、右側輪同時加載，未試驗加載的計算輪位與試驗輪位作用下的應力變化規律存在重演現象，因應力橫向影響區域大于車寬，左、右輪作用存在疊合區間。相對無鋪裝狀態，鋪裝對測試部位應力均存在改善，新鋪裝狀態下，測試部位受力與高低溫環境有強關聯性。

3.4 鋼橋面板變形分析

鋼橋面板典型測點(D3)撓度與橫向加載線的關系如圖14 所示。試驗加載輪位作用下測試部位應力實測與理論計算變化規律一致，撓度橫向影響區域約為4 道U 肋間距(2480 mm)。當控制輪中心位于面板測點臨近U 肋腹板頂部時面板變形達到峰值，受加載輪雙胎凈距的影響，當控制輪中心位于面板測點頂部時面板變形有所回落。因考慮了左、右側輪同時加載，未試驗加載的計算輪位與試驗輪位作用下的變形變化規律存在重演現象，因變形橫向影響區域大于車寬，左、右輪作用存在疊合區間。結果表明相對無鋪裝狀態，鋪裝對測試部位變形均存在一定改善，面板變形與高低溫環境有強關聯性。

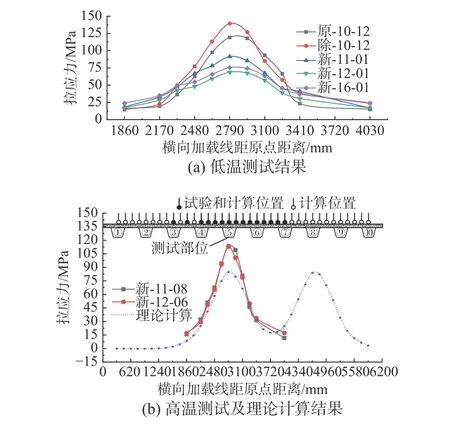
圖13 L1、L2 測點平均應力測試結果Fig.13 Average stresses of L1 and L2

圖14 典型測點撓度測試結果Fig.14 Measured deflection at typical measuring points

3.5 結果對比分析

對比實測與理論計算結果可知，最不利試驗荷載作用下理論計算結果與新鋪裝完成時(新-11-01)實測結果相近，具體分布見表2。

不同測試部位歷次試驗不利值見表3，相對無鋪裝狀態不同試驗條件下鋼橋面板受力及變形改善效果見表4。

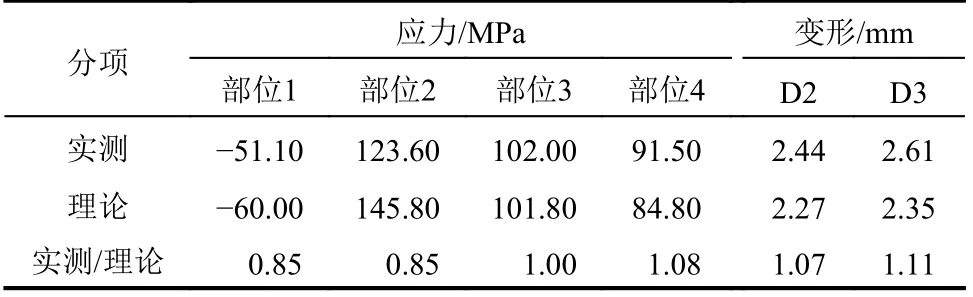
表2 實測與理論計算結果對比Table 2 Measured and theoretical calculation results

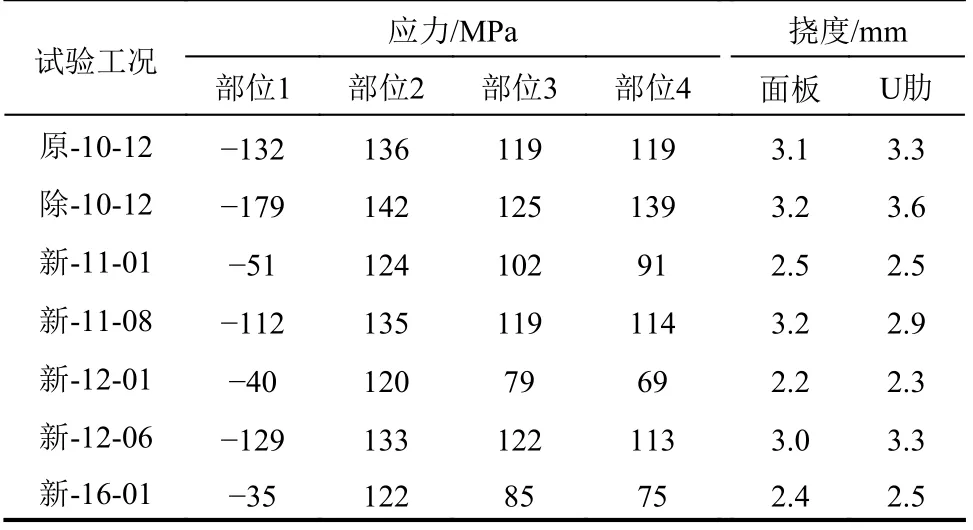
表3 不同測試部位歷次試驗不利值統計Table 3 Statistics of critical measurements of corresponding regions

表4 應力及變形改善效果Table 4 Stress and deflection improvement effects

1) 從應力值看，鋼橋面板4 個疲勞敏感區域在試驗荷載作用下承受較大的應力，原鋪裝狀態下測試部位應力絕對值為119 MPa～136 MPa，鋪裝鏟除后為125 MPa～179 MPa，新鋪裝高溫環境下為113 MPa～133 MPa。

2) 從新鋪裝改善效果看，在低溫環境下，鋪裝運營6 年后，疲勞敏感部位1～4 應力改善效果分別為80%、14%、32%、46%，面板變形改善27%，U 肋變形改善31%，新鋪裝改善效果優于相近環境下原有鋪裝的改善效果。

3) 4 個疲勞敏感部位實測應力隨環境溫度的變化關系如圖15 所示，各部位應力與環境溫度存在線性關聯，隨溫度變化的速率k值差異較大(k1=?4.00，k2=0.64，k3=1.89，k4=1.91)。疲勞敏感部位應力與溫度線性關聯的特點與文獻[13?14]基于鋼橋面板的監測結果所揭露的現象一致。

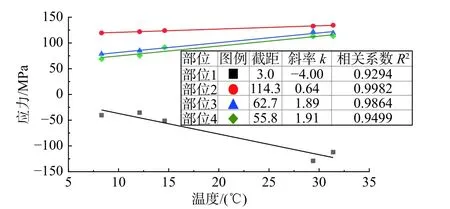
圖15 疲勞敏感部位實測應力與溫度關系Fig.15 Stress of sensitive regions of fatigue crack with temperature

4 考慮溫度的疲勞壽命改善效果分析

4.1 橋梁整體溫度環境

為考察背景橋梁所處自然溫度環境，從當地氣象部門獲取了一整年365 d 的實測結果作為分析樣本，數據來源于橋址附近3 km 氣象部門布設的觀測站記錄。一年期整點溫度時程如圖16 所示。

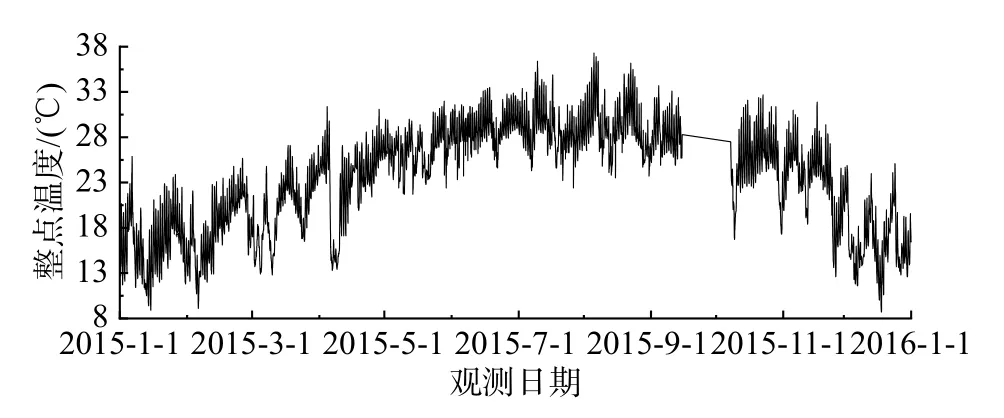
圖16 一年整點溫度記錄Fig.16 Hourly temperature record of one whole year

由4 個疲勞敏感部位實測應力與溫度存在線性關聯，為修正溫度對應力的影響，特將歷次測試結果修正至年均溫度。為獲取某時間區段內平均溫度，采用復化梯形求積公式(2)[15]求得溫度沿時程的積分。

式中：Tn為積分值；n為積分點數目，可按逐月或逐年取值；hk為積分步長，取為1h；f(xk)為k時刻溫度值；f(xk+1)為k+1 時刻溫度值，平均溫度為Tn除以n。按照本方法求得年均溫度為23.7 ℃。

4.2 疲勞壽命改善效果分析方法

國內外規范中橋梁鋼結構抗疲勞設計均是著眼于細節構造，對易發生疲勞破壞的細節構造進行分類疲勞評定，不同細節構造類別對應不同的Δσ-N曲線[16]。Δσ-N曲線方程式一般在雙對標坐標中表示，如下式：

式中：N為對應Δσ 作用下的疲勞循環次數，即疲勞壽命；Δσ/MPa 為外加應力幅；A為曲線的截距；m為曲線斜率，日本規范中取值為3，中國及歐洲規范分段考慮，分別為3 和5，如圖17 所示[1]；C為循環次數的統計偏差。

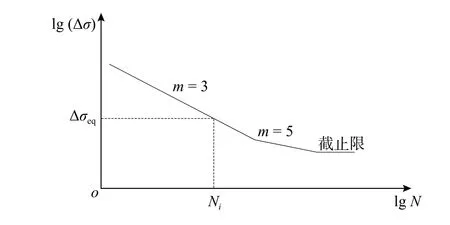
圖17 細節構造Δσ-N 曲線特點Fig.17 Typical Δσ-N curve for a fatigue vulnerable location

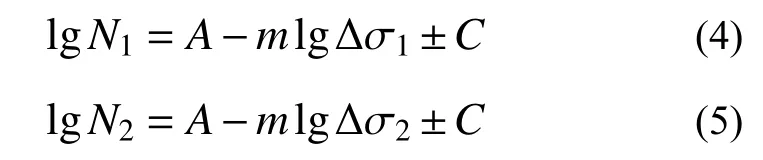
式(4)和式(5)分別為某評定部位在應力幅Δσ1及應力幅Δσ2作用下其疲勞壽命N1及N2的求解公式，將式(4)減去式(5)可得：

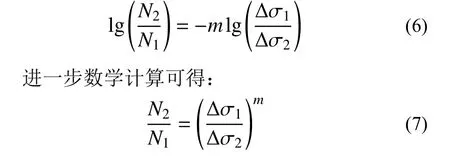
由式(7)可推算兩種不同應力幅狀態下的壽命比值，由此可見兩種不同應力幅狀態下的疲勞壽命相對改善效果主要由所采納的Δσ-N曲線斜率m及對應的應力幅值有關，與具體構造細節的Δσ-N曲線方程已無直接聯系。

由于正交異性鋼橋面板的疲勞敏感部位應力梯度較大，名義應力取值位置不同會導致疲勞評估結果即可能出現較大差異，部分學者結合足尺模型試驗提出了熱點應力法、切口應力法、結構應力法用于提高鋼橋面板疲勞性能評估的準確性[17?21]，雖然存在諸如之上的不同應力計算方法，但最終疲勞壽命評估時仍回歸至線性累積損傷模型之上，且在高應力水平所采納的Δσ-N曲線斜率m大多仍取值3，本文以兩種鋪裝狀態下的應力實測結果基于式(7)對疲勞改善效果進行分析，式(7)中狀態1 表示原鋪裝狀態，狀態2 表示新鋪裝狀態。當結構處于線彈性狀態、同一考察部位不同測試狀態下應力縱橫向影響范圍及規律保持一致時，可以認為在荷載特征保持不變時應力峰值之比(σ1/σ2)與應力幅之比(Δσ1/Δσ2)一致，即可以將考察部位的實測應力峰值帶入式(7)進行疲勞壽命相對改善效果評估。

4.3 疲勞壽命相對改善效果

基于圖15 中各部位實測應力與溫度的關系，按年均溫度對實測應力進行修正，代入式(7)計算鋪裝更換前后4 個疲勞敏感部位壽命相對改善效果，結果見表5。相對原鋪裝狀態，新鋪裝對部位1 疲勞壽命改善較大，約提高了2.95 倍，對部位4 疲勞壽命改善次之，約提高1.64 倍，對于部位2、3 疲勞壽命改善效果不明顯。

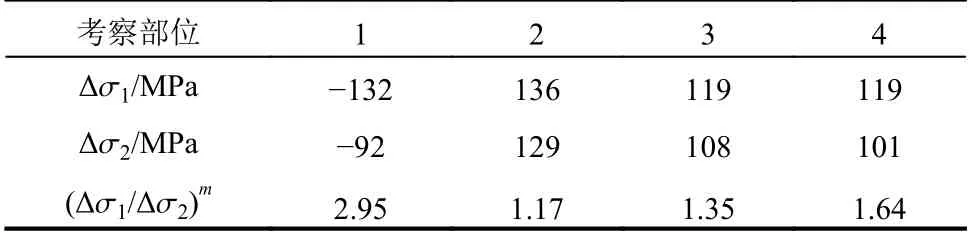
表5 新鋪裝對疲勞敏感部位壽命相對改善效果Table 5 Relative fatigue life improvement of sensitive regions with new pavement

需要說明的是本文背景橋梁歷次實橋試驗均于測試當日夜間0:00～3:00 區間開展，此時間段內環境溫度較為穩定，且環境溫度與鋪裝溫度相對一致，而橋面鋪裝在運營使用過程中其溫度與自然環境溫度變化存在一定的滯后性和非線性，尤其在夏季鋪裝長期處于高溫工作狀態，其溫度要明顯高于環境溫度，相應改善效果較表5 中的理論推算值偏低。

5 結論

為考察環氧瀝青混凝土鋪裝對正交異性鋼橋面板受力影響，對某懸索橋鋼箱梁建立了有限元模型，開展了長達6 年的現場試驗，試驗涵蓋原鋪裝、鋪裝鏟除、新鋪裝三種狀態，測試了疲勞敏感部位受力及構件變形規律，開展了考慮溫度影響的疲勞壽命改善效果分析研究，結果表明：

(1) 背景橋梁鋼橋面板4 個疲勞敏感部位受力規律及隨溫度變化的趨勢6 年來未發生明顯改變，說明環氧瀝青混凝土鋪裝與鋼橋面板間組合受力處于穩定狀態。

(2) 在低溫環境下，鋪裝運營6 年后，疲勞敏感部位1～4 應力改善效果分別為80%、14%、32%、46%，面板變形改善27%，U 肋變形改善31%。

(3) 4 個疲勞敏感部位實測應力與溫度存在線性關聯，應力隨溫度變化的速率k值差異較大(k1=?4.00，k2=0.64，k3=1.89，k4=1.91)。

(4) 部位1、4 應力及鋼橋面板變形影響范圍及變化規律的實測與理論計算結果吻合較好，部位2、3 應力實測與理論計算存在輕微偏差，僅通過有限元計算開展疲勞分析存在局限性。

(5) 將實測應力統一至年均溫度后，相對于原鋪裝，新鋪裝對部位1 疲勞壽命改善較大，約提高了2.95 倍，對部位4 疲勞壽命改善次之，約提高1.64 倍，對于部位2、3 疲勞壽命改善效果不明顯，高溫環境下部位2、3 開裂可能性仍較大。