基于SPEI的甘肅省干旱特征分析

王阿靜，王 偉

(1.永壽縣水利管理站, 陜西 永壽 713400;2.武功縣自來水公司，陜西 武功 712200)

干旱是一種頻繁發生的自然現象，會對區域社會經濟、生態環境、和人類生活造成極大的威脅[1-2]。隨著全球氣候變化加劇，導致部分地區干旱事件發生頻率呈增加趨勢[3-4]。因此需要對干旱的發生及變化特征進行深入研究。

由于對干旱研究的特點各異，干旱的分類也不盡相同，美國氣象學會在總結各種分類的基礎上將干旱分為4類：氣象干旱、農業干旱、水文干旱和社會經濟干旱[5]。氣象干旱是引起其他干旱的前提，其他干旱都是氣象干旱的影響結果，因此，準確監測氣象干旱對于旱災的預防、緩解等有重要意義。干旱指標是研究干旱的有力工具，其中，標準化降水指數(SPI)和帕爾默干旱指數(PDSI)是使用廣泛的干旱指數。但是，SPI指數只考慮降水量的影響，忽略下墊面、作物及其他相關因素的影響，只能大致反映干旱發生趨勢，不能準確反映某時段干旱發生程度[5]，PDSI指數對于不同區域、不同時間尺度的干旱監測對比性較差。Vicente-Settano[6]提出的標準化散發指數(SPEI)，其算法與SPI類似，而變量為降水(P)與潛在蒸散發(PET)的差值D，D表征某區域特定時間尺度下水量盈余或缺乏程度。SPEI指數基于水量平衡原理，同時又可表征不同時間尺度的干旱特征，自提出后便得到了廣泛應用。

以往關于對干旱事件的研究側重對單變量干旱特征的研究，然而，單變量干旱特征很難表征干旱事件變化規律。因此，完整地描述干旱事件對多個干旱特征變量進行聯合，研究多變量干旱特征的發生規律。本文首先根據甘肅省25個氣象站點的月降水、溫度數據計算得到了1982年—2015年的月SPEI指數序列值，然后利用游程理論進行干旱識別，利用Copula函數構建干旱歷時、烈度的聯合分布，計算其聯合概率分布狀況及重現期，為甘肅省干旱預警提供科學依據。

1 數據與方法

1.1 數據來源

利用1982年—2015年間甘肅省地面氣象觀測站的月降水、平均溫度數據，數據來源于中國氣象數據網(http://data.cma.cn/)。選擇研究區域內25個氣象站點(見圖1)。將干旱劃分為輕、中、重旱3個程度。

圖1 甘肅省25個氣象站分布

1.2 研究方法

1.2.1 標準化降水蒸散指數(SPEI)[7]

(1) 本文采用Thornthwaite公式計算潛在蒸散量：

(1)

式中：K為修正系數；T為月平均氣溫；I為年總加熱指數；m是由I決定的系數。

(2) 逐月計算降水與潛在蒸散的差值：

Di=Pi-PETi

(2)

式中：Pi為月降水量；PETi為月潛在蒸散量。

(3)采用三參數的Log-logistic分布對Di進行擬合，得出累積概率函數：

(3)

(4)

式中：α為尺度參數;β為形狀參數;γ為Origin參數;f(x) 為概率密度函數;F(x) 為概率分布函數。

(4)利用正態逆變換求出SPEI：

(5)

(6)

式中：P≤0.5 時，P=F(x)；當P>0.5 時，P=1-F(x)；C0=2.515517，C1=0.802853，C2=0.010328，d1=1.432788，d2=0.189269，d3=0.001308[7]。

對甘肅省25個氣象站的氣象數據進行處理，得到1982年—2015年的SPEI，利用1個月時間尺度的SPEI分析甘肅省干旱時空變化規律，并進行登記劃分(表1)。

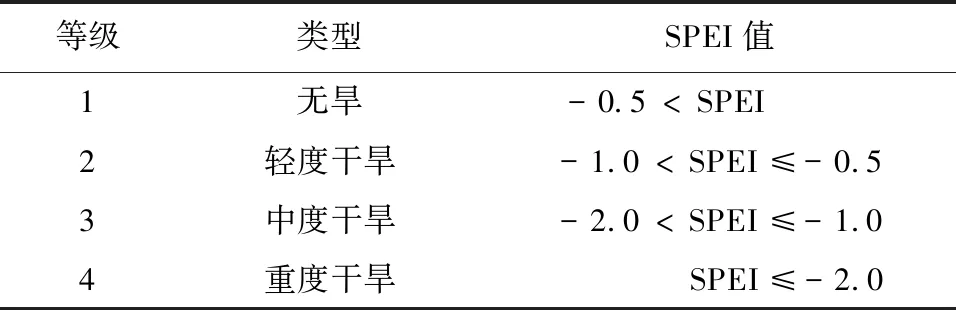
表1 標準化降水蒸散指數干旱等級劃分

1.2.2 干旱識別

以游程理論為工具，從計算的SPEI 序列中識別出干旱歷時和烈度2個特征變量。干旱歷時表示一次干旱事件從發生到結束所持續的時間，干旱烈度為在該次干旱事件過程中SPEI累計值的絕對值之和，設定3個截斷水平X0、X1和X2，干旱事件的識別過程為[1]：

(1)當SPEI 值小于X1時，則初步判定此月發生干旱。

(2) 對于干旱歷時為1個月的干旱事件，當其SPEI值大于X2，則認為此月沒有發生干旱，將其剔除。

(3)當相鄰2次干旱過程的時間間隔僅為1個月，且該月內的SPEI值小于X0，則將這2次相鄰干旱過程合并為1次干旱事件，干旱歷時為兩次干旱歷時之和加1，干旱烈度為2次干旱事件的烈度之和，否則為2次獨立的干旱過程。計算過程取X0=0，X2=-0.5，X1=-0.3。

1.2.3 邊緣分布

干旱歷時、烈度的邊緣分布函數分別表示為FD(d)和FS(s)，干旱烈度的邊緣分布類型選為伽馬分布，干旱歷時的邊緣分布函數選為威爾布分布。

1.2.4 聯合分布函數

Copula基于變量間的相關性對變量特征進行聯合。干旱歷時、烈度聯合分布函數為：

F(d,s)=P(D≤d,S≤s)=C(FD(d),FS(s))

(7)

本文選擇常用的Frank-Copula作為聯接函數。

1.2.5 重現期計算

干旱歷時和干旱烈度的單變量聯合重現期為：

(8)

(9)

式中:T(d)和T(s)分別表示干旱歷時、烈度的重現期；N為干旱系列長度，34 a；n為干旱事件次數，表示干旱事件發生的總次數。

兩變量的聯合重現期為：

(10)

2 結果與分析

2.1 干旱事件特征分析

根據游程理論提取出1982年—2015年間各個氣象站點發生干旱事件的干旱歷時、干旱烈度，統計出干旱事件的發生頻次以及干旱等級，1982年—2015年間甘肅省出現的最低干旱事件頻次為130次，最高150次，甘肅北部是主要的旱災頻發區，南部地區干旱發生頻率相對較小(見圖2)。而重旱發生頻率較高的站主要集中在甘肅東部，最高為7次。

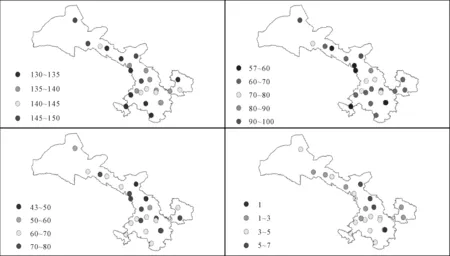
圖2 1982年—2015年間甘肅省不同等級干旱發生頻次空間分布

2.2 基于Copula的干旱事件聯合分布

2.2.1 單變量線型擬合

對于干旱歷時，通常會選用威爾布分布，對于干旱烈度，通常會選用伽馬分布，本文以馬鬃山站和酒泉站為例，分別對干旱歷時、干旱烈度的擬合分布函數進行分析。結果表明，干旱烈度的擬合效果更好，理論分布與經驗分布的匹配程度更佳，這主要是因為干旱歷時重復點較多，導致其分布稀疏，使得理論配線效果不佳，但是仍能通過KS檢驗。因此，對干旱歷時采用威爾布分布，對干旱烈度采用伽馬分布進行配線(見圖3、圖4)。

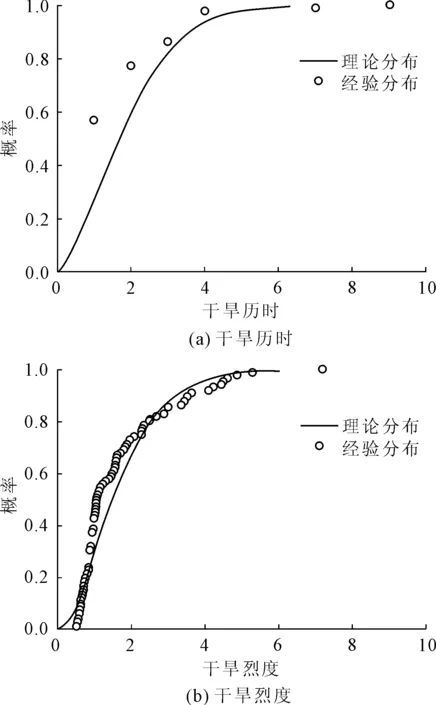
圖3 馬鬃山站干旱歷時、干旱烈度經驗分布與理論分布

圖4 酒泉站干旱歷時、干旱烈度經驗分布與理論分布

2.2.2 干旱歷時和干旱烈度的聯合概率分布

分別利用威布爾分布和伽馬分布干旱歷時、烈度配線，利用Frank Copula函數進行聯合，如圖5、圖6所示，隨著干旱歷時、干旱烈度概率值的不斷增大，累計概率的值也不斷增大。表明隨著干旱歷時，干旱烈度的增大，其聯合事件的發生概率也隨之增大，馬鬃山站與酒泉站干旱事件以干旱歷時與干旱烈度同步的情況最多，長歷時伴隨著高烈度干旱情況。除此，也有短歷時高烈度干旱事件發生，此類干旱事件的干旱烈度比較大，短時期內發生了嚴重的水資源短缺狀況。

圖5 馬鬃山站干旱歷時、烈度聯合概率等值線圖

圖6 酒泉站干旱歷史、烈度聯合概率等值線圖

2.2.3 干旱歷時和干旱烈度的聯合重現期

以馬鬃山和酒泉兩個站點為例，單變量干旱事件(歷時、烈度)的重現期隨歷時增長、歷時增大呈增大趨勢(見圖7)，馬鬃山站干旱歷時為6個月時，干旱歷時重現期超過80 a，酒泉站干旱歷時為6個月時，干旱重現期僅為40 a。通過聯合概率計算，得到了兩站的干旱歷時與干旱烈度的聯合重現期(見圖8)，當干旱歷時、烈度達最大時，馬鬃山站干旱聯合重現期為5 a，酒泉站的聯合重現期為4.5 a(見圖9)。

馬鬃山和酒泉站所在區域的聯合重現期隨歷時和烈度的增加都呈增加趨勢，酒泉站趨勢變化更加顯著，對不同干旱事件的重現期進行正確估計，可以為農業氣象干旱預防治提供更加科學的指導[1]。

3 結 論

利用甘肅省25個氣象站的月降水溫度數據計算出了月SPEI系列數據，基于游程理論識別甘肅省在1982年—2015 年間的干旱事件的歷時和烈度，利用Copula函數將干旱歷時與烈度進行聯合，分析聯合累計概率和聯合重現期，主要結論如下：

圖7 馬鬃山站、酒泉站干旱歷時及干旱烈度重現期

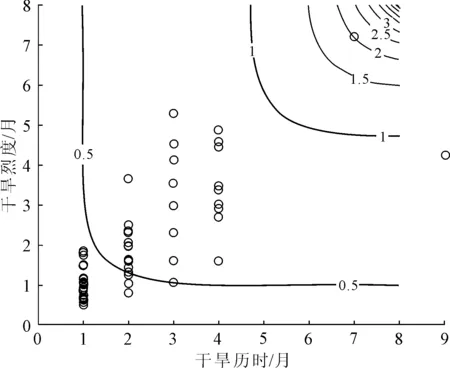
圖8 馬鬃山站干旱歷時、烈度聯合重現期

(1) 甘肅省出現最低干旱發生頻次為130次，最高為150次，甘肅北部是主要的干旱災害頻發區，南部地區干旱發生頻率相對較小。

(2) 采用Frank-copula函數對干旱兩變量進行擬合，建立聯合分布函數分析干旱特征變量的聯合累計概率及聯合重現期。

圖9 酒泉站干旱歷時、烈度聯合重現期

(3) 隨著干旱歷時、烈度的不斷增加，二者的聯合累計概率和聯合重現期也呈增加趨勢。