基于小波理論的電力系統故障診斷研究
鄭秋元,符 云,陳大華,胡加旺
(1.海南電網有限責任公司,海南 海口 570203) (2.海南電網有限責任公司輸變電檢修分公司,海南 儋州 571700)
電力系統在國民經濟發展中起到了至關重要的作用,電力系統故障診斷技術的研究對快速恢復電力系統功能、減少經濟損失意義重大。伴隨著電力系統規模的不斷擴大,各種大容量的發電機組和超高壓輸電系統相繼投入使用,這使得電力系統變得越來越復雜[1]。受到自然環境、電力系統元件制造質量等因素的影響,電力系統中各個組成部件發生故障的概率大幅度增加。電力系統故障的出現對整個電力系統安全運行以及電力系統設備都會產生不利的影響,其中電力系統短路故障的危害尤其巨大[2]。短路故障使得電流超過額定電流許多倍,極易導致電氣設備發生故障。對電力系統故障進行診斷是為了快速找出故障所在,從而避免重大電力系統安全事故的發生。傳統的電力系統故障診斷方法是基于傅里葉分析的,結構相對比較簡單,性能也相對比較穩定、可靠。電力系統故障通常會使得采集到的信號中含有短時突變成分,而這些短時突變成分正是實施故障診斷的關鍵。由于傅里葉分析無法實現對信號的時頻局部化分析,因此不適合用于分析電力系統故障中的突變信號。而小波分析方法具有良好的時頻局部化能力,對包含短時突變成分信號的分析效果顯著,這使得其在電力系統故障診斷中得到廣泛應用[3]。基于此,本文采用小波理論對電力系統故障診斷進行研究。
1 理論基礎
1.1 小波變換
小波變換具有良好的時頻局部化能力,是進行信號時頻分析和處理的理想工具[4]。設函數f(t)為平方可積函數,函數f(t)的連續小波變換定義為:
(1)
式中:Wf(a,b)為函數f(t)的小波變換;函數ψ(·)為母小波;a為尺度參數;b為平移參數;t為時間。

(2)
式中:j為層數;k為水平數;a0為尺度參數;b0為平移參數。
1.2 信號奇異性
信號的奇異性常常采用Lipschitz指數來度量。對平方可積函數f(t),如果?K>0和m=[α](表示不超過α的最大整數)次多項式pb(t)使得對?t∈R滿足[5]式(3),那么稱函數f(t)在點b處有Lipschitz指數α。
|f(t)-pb(t)|≤K|t-b|α
(3)
式中:K為階數。
如果?K>0使得對?b∈[m,n]均有式(3)成立且K和b無關,那么稱函數f(t)在區間[m,n]上有一致Lipschitz指數α,其中m和n分別為區間的下限和上限。Lipschitz指數α反映了函數在該點奇異值的大小,指數α越大說明函數f(t)在該點的光滑性越好,指數α越小說明函數f(t)在該點的奇異性越大。
2 電力系統故障診斷算法
2.1 低頻和高頻系數
小波分析方法具有良好的時頻局部化能力,對信號進行小波變換的過程就是將信號分解為低頻系數和高頻系數的過程,對原始信號進行小波變換就能完成數據降維和特征提取。小波分解是通過不同尺度小波基與實測信號進行內積運算的過程,常用的小波分解算法是Mallat算法。實測電力系統故障信號通過Mallat分解得到尺度系數和小波系數,其中尺度系數產生的信號為實測電力系統故障信號的低頻部分,小波系數產生的信號為實測電力系統故障信號的高頻部分[6]。
2.2 信號奇異性檢測
選擇適當的小波基對實測電力系統故障信號進行小波分解得到故障信號的高頻部分,通過對高頻部分的分析就可以檢測信號的奇異點,獲得電力系統發生故障的時刻,但是卻無法確定電力系統發生故障的位置。為了找出電力系統故障點的位置,需要采用模極大值算法對電力系統每一個采樣點進行進一步的檢測。當電力系統發生故障時,如果故障暫態信號是奇異的,可以通過信號中的奇異點來診斷電力系統發生故障的時刻[7]。由于信號的奇異點為小波變換的模極大值點,但是模極大值點未必是信號的奇異點,因此采用小波方法對電力系統進行故障診斷時常常采取設置門限值的方式。如果模極大值大于門限值,那么認為在該位置、該時刻發生故障;如果模極大值小于門限值,那么認為在該位置、該時刻未發生故障[8]。采用小波理論對電力系統突變信號奇異點的位置檢測算法流程如下:
1)對電力系統突變信號采用Mallat算法進行小波分解,分解得到最高層低頻系數和高頻系數,并計算小波變換系數的最大值Wmax;
2)對閾值Wflat和時間長度Tflat進行設置;
3)結合時間長度Tfiat篩選小波變換系數模極大值,確定篩選閾值T1=aWmax和T2=bWmax,如果同時滿足
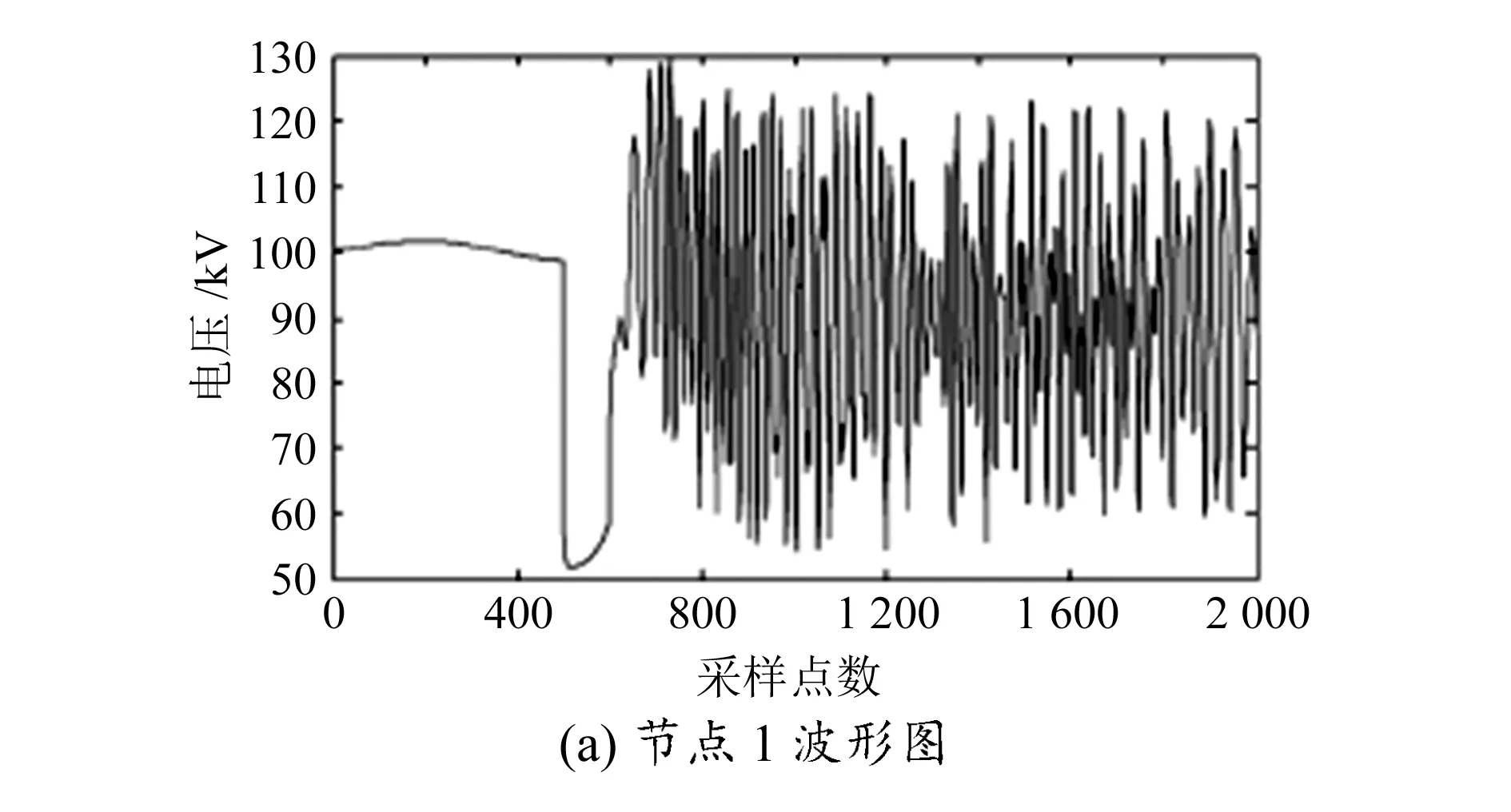
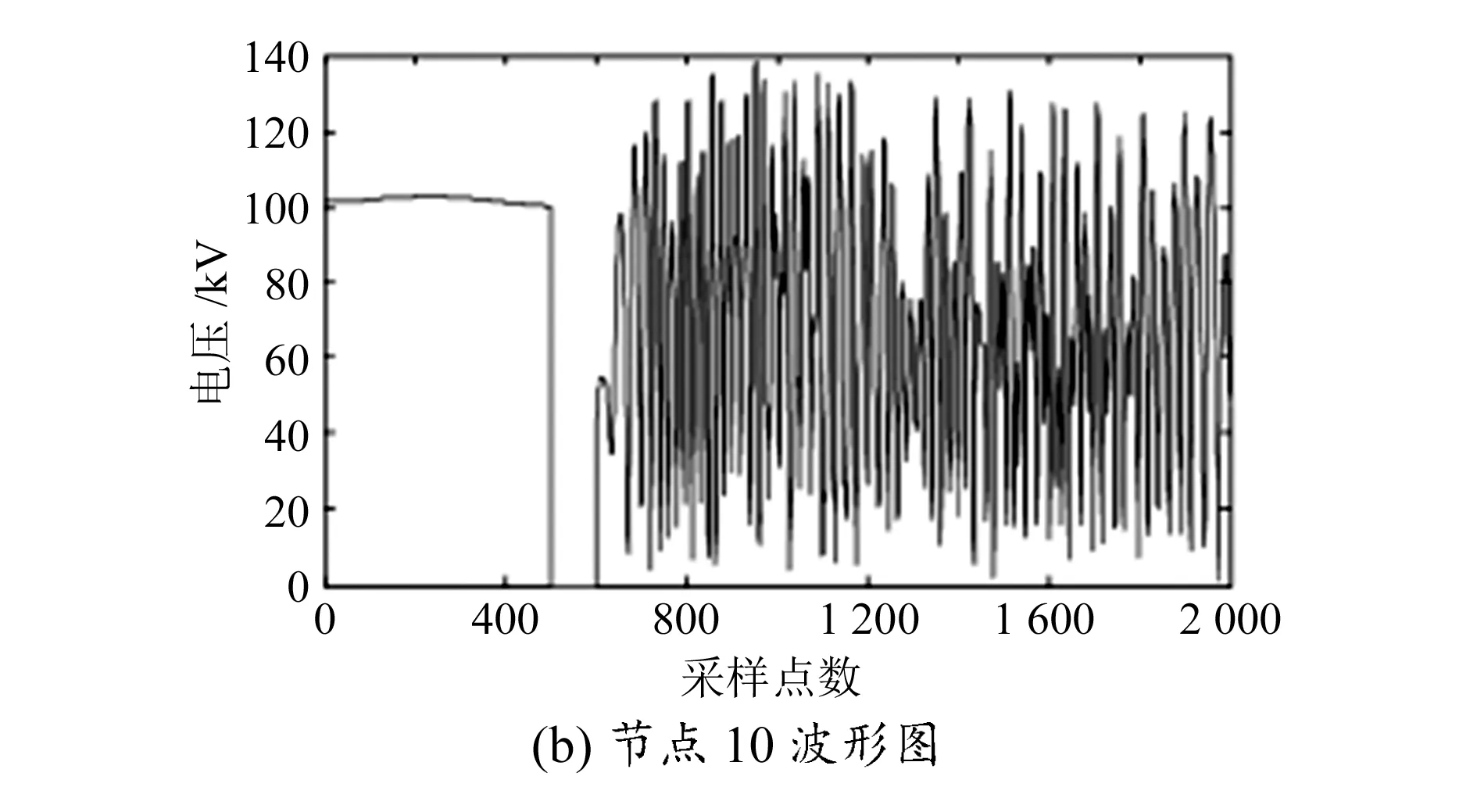
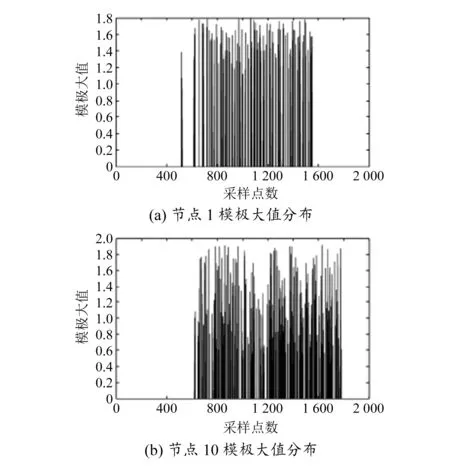
T1 (4) Wf(i+1)-Wf(i)>Wfiat (5) 那么保留模極大值,否則不保留模極大值。 4)觀察保留下來的模極大值的分布,從而實現對電力系統故障時刻和故障位置的診斷。 圖1為基于小波理論的電力系統故障診斷流程圖。 圖1 電力系統故障診斷流程 本文分析的數據來源于IEEE39節點系統,數據的采樣間隔為10 ms,采集數據的時長為20 s。IEEE39節點系統在5 s時、節點10處發生接地短路,在6 s時故障切除。選擇首段節點(節點1)和故障節點(節點10)的數據,繪制電力系統在典型節點的波形,如圖2所示。 圖2 電力系統在典型節點波形圖 對節點1波形和節點10波形進行小波分解,小波基選擇db3,分解層次為6層。提取節點1和節點10在第6層的低頻小波系數來對實測電力系統故障信號進行逼近可以起到對原始信號降噪的效果。分別提取節點1和節點10在第6層的高頻小波系數,得到的波形圖如圖3所示。 圖3 電力系統在典型節點的細節波形圖 由圖3可見,對電力系統故障信號進行小波分解得到的高頻系數可以很好地反映細節波形,能清楚地觀察到原始信號的不連續點。基于傅里葉變換的頻域分析方法不具有時間分辨率,因此在電力系統故障診斷方面顯得無能為力。借助于小波分析對原始信號進行小波分解,提取高頻系數可以更為精準地檢測到原始信號的突變時刻。從小波細節波形圖可知,在第500個數據處出現了奇異點,因此可以做出電力系統在5 s時出現故障的判斷。 在判斷出電力系統發生故障的時刻后,還要對電力系統出現故障的位置進行判斷:對原始電力系統故障信號進行小波分解并提取低頻小波系數,同時通過設置的閾值來對模極大值點進行保留或刪除處理,并將保留的模極大值繪制成圖,最后通過觀察模極大值的分布實現對電力系統故障的定位。本文選擇小波系數閾值Wfiat=0.02Wmax,時間長度Tfiat=T+L/2.5,其中T為Wmax出現的時刻,L為設置的時間長度。篩選模極大值,確定閾值T1=aWmax和T2=bWmax,其中參數a=0.19,b=0.68。滿足式(6)和式(7)的模極大值保留,不滿足的刪除。 0.19Wmax (6) |W(i+1)-W(i)|>Wflat (7) 由于已經確定該電力系統在5 s時刻發生了故障,因此只需要關注在5 s前后模極大值是否存在即可。對節點1和節點10的模極大值進行篩選,保留的模極大值分布如圖4所示。 圖4 電力系統典型節點模極大值分布圖 由于電力系統在5 s時發生了故障,因此在進行電力系統故障定位時僅僅是觀察5 s前后的模極大值分布情況。如果在某個節點前后均保留了模極大值,那么該節點不是故障節點;如果在某個節點前后均沒有保留模極大值,那么該節點為故障節點。通過圖4可知,節點1前面保留了模極大值,而節點10前后均沒有保留模極大值,故節點10為電力系統的故障節點。 本文對小波理論在電力系統故障診斷中的應用進行了研究,提出了基于小波高頻系數和模極大值奇異性檢測相結合的故障時刻診斷和故障定位的方法,并通過實例證明了本文所提方法的有效性。本文的研究對電力系統故障診斷具有一定的參考價值。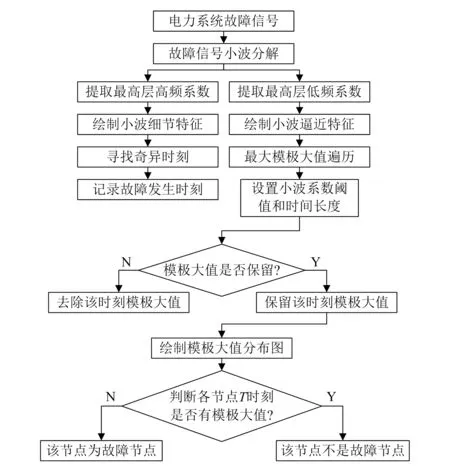
3 實例分析
3.1 數據來源
3.2 故障診斷

4 結束語

