風電傳動系統軸承多目標優化設計

袁海良，邱 俊，王 智，王德倫

(大連理工大學機械工程學院, 遼寧 大連 116024)

作為風力發電機組的核心部件，主軸傳動系統軸承的性能直接影響軸系的安全性、穩定性。設計軸承的過程中，評價指標不同會導致軸承結構參數的差異。目前，軸承結構設計的效率低、周期長，如何改進軸承的設計方法成為提高軸承結構設計效率的關鍵。

近年來國內外學者對軸承的優化設計均做了相關的研究。文獻[1]通過ISIGHT與MATLAB軟件的聯合運用完成雙列圓錐滾子軸承(DTRB)的優化設計；文獻[2]將改進的自適應遺傳算法應用于圓錐滾子軸承的優化設計；文獻[3]基于遺傳算法進行了雙列圓錐滾子軸承的優化設計；文獻[4]綜合研究了雙列圓錐滾子軸承的受力及潤滑狀況；文獻[5]在實驗數據和理論模型的基礎上，將有限元法與多響應面優化相結合，尋找到雙列圓錐滾子軸承的最佳運行工況；文獻[6]基于FEM(finite element method)與RSM(response surface methodology)對圓柱滾子軸承(CRB)進行優化設計；文獻[7]借助MATLAB的fmincon命令完成圓柱滾子軸承的優化設計；文獻[8]運用遺傳算法完成了圓柱滾子軸承的優化設計；文獻[9]運用人工蜂群算法完成了圓柱滾子軸承的多目標優化設計。當前的研究方法多數只考慮單目標優化，且未綜合考慮軸系中的全部軸承。為此，本文以某型號雙饋式風電機組的軸系為例，在綜合考慮全部軸承的基礎上，建立其優化的數學模型，借助MATLAB實現軸承的結構參數優化設計。

1 結構式與力學模型

風機主軸系有各種不同的結構[10]，如圖1所示為雙饋式機型中典型的軸系結構，雙列圓錐滾子軸承與圓柱滾子軸承構成載荷支點，支撐轉軸從而構成軸系，轉軸的法蘭與風機輪轂連接，載荷由輪轂傳遞至軸系。

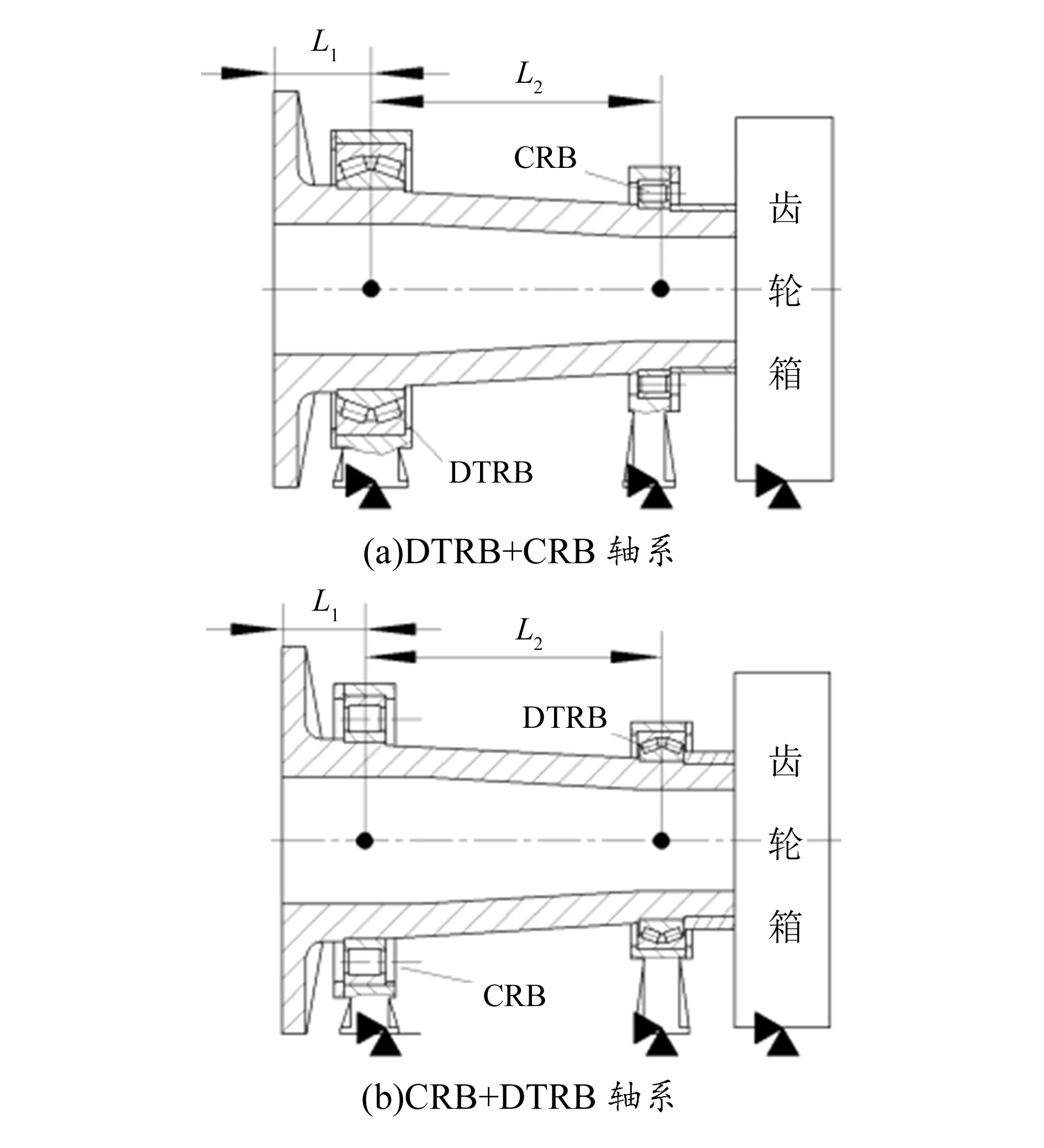
圖1 典型軸系結構示意圖

主軸與齒輪箱之間通常采用柔性連接，抽象簡化出的軸系力學模型如圖2所示，圖中O點為法蘭載荷作用點，其坐標系參考GL規范[11]要求，O1和O2為軸承載荷點，L1和L2為各載荷點之間的距離；Mxm,Mym,Mzm,Fxm,Fym,Fzm為外載荷，Fx1,Fy1,Fz1為O1支點的載荷，Fx2,Fy2,Fz2為O2支點的載荷。

圖2 軸系力學模型圖

將空間力系轉化為Oxy與Oxz平面力系，以O點為坐標原點，得到平面內O1和O2點的載荷。

在Oxy平面內FOxy為：

(1)

在Oxz平面內FOxz為：

(2)

由此得到O1點與O2點軸承的徑向力為：

(3)

式中：FO1與FO2分別為O1,O2點的載荷。

對于軸向力，當O1支點為DTRB時，Fx1=Fxm,Fx2=0；當O1支點為CRB時，Fx1=0,Fx2=Fxm。根據以上力學分析，得到軸承承受的載荷FB為：

(4)

式中：Ftd,Ftr分別為DTRB的軸向力與徑向力；Fcd,Fcr分別為CRB的軸向力與徑向力；A為2×2階矩陣，當A為單位對角矩陣時，表示O1支點為DTRB，當A為單位反對角矩陣時，表示O1支點為CRB。

2 優化模型

軸承的體積、壽命均為評價軸承設計結果的指標，體積反映了生產軸承所消耗材料的量，壽命反映了軸承運行時間的長短。

在軸承中，套圈與滾子存在配合關系，因此其尺寸參數之間相互制約。將尺寸變量分為自變量與相關變量，套圈內外徑、厚度等參數在設計時可以在一定的范圍內變動，則這些尺寸參數為自變量；滾子直徑、長度等參數可以根據套圈等的尺寸得到，則這些尺寸參數為相關變量。

優化模型需要確定5個方面的問題：目標函數、約束函數、優化變量、優化算法以及結束準則。

建立目標函數與約束函數時，為了避免軸承相同參數表達的冗余，以下角標i表示軸承類型，i=c,t，其中c表示CRB，t表示DTRB。

2.1 目標函數

目標函數是優化模型中的核心內容，需要清晰而又準確地建立。考慮到DTRB結構的對稱性，以單列軸承為基礎進行分析，圖3所示為軸承結構示意圖。

圖3 軸承結構示意圖

1)軸承體積。

軸承的體積越小，生產時消耗的材料越少，因此可以選擇軸承體積作為優化目標。對于體積函數，尺寸變量在定義域內的迭代變化必然引起函數值的改變，函數值的減小意味著軸承體積減小。

軸承體積VA為CRB與 DTRB體積的代數和：

VA=Vio+Vii+ViR

(5)

式中：Vio為外套圈體積；Vii為內套圈體積；ViR為滾子體積。

2)軸承壽命。

在軸承設計中，壽命是評判軸承的重要標準，壽命值越大，則軸承可運轉時間越長，因此可以選擇軸承壽命作為優化目標。軸承壽命與其結構尺寸之間的關系為非線性關系，尺寸變量在定義域內的迭代變化必然引起函數值的改變，函數值的增大意味著軸承壽命延長。

根據ISO281標準[12]，軸承修正壽命Lim表示為：

(6)

式中：Ci為基本額定動載荷；Pi為當量動載荷；αi1為可靠度壽命修正系數；αiISO為壽命修正系數。

由于CRB、DTRB的結構與承受載荷的差異，一般情況下兩個軸承的壽命并不能保證相同，因此軸承壽命LA以其中最小者為準：

LA=min(Lcm,Ltm)

(7)

2.2 約束函數

軸承的結構尺寸必須保證軸承工作時運轉順暢，各部分之間不存在干涉，同時為了確保工作時機組的安全性，軸承需要滿足相應的性能要求。

考慮軸系的裝配關系，O2處軸承內徑必須小于O1處軸承內徑：

Ψcdc+Ψtdt≤0

(8)

式中：Ψc,Ψt為控制O1,O2處軸承內徑關系的系數，且[Ψc,Ψt]=A[1,-ξ]T，ξ∈(0,1)。

對于風電機組的CRB，內圈厚度Cc與外圈厚度Bc一般相同：

Cc-Bc=0

(9)

對于風電機組的DTRB，根據滾子與套圈的配合關系，可以得到：

(Bt-a0-a1)cosα+(Ct-C2-C3)cos(α-2φ)=0

(10)

式中各參數的含義如圖3所示。

軸承結構既要保證滾子不碰撞，又要避免滾子分布過于稀疏，因此根據滾子分布的幾何關系可得：

(11)

式中：Zi為滾子個數；Diwe為滾子直徑；Dipw為滾子節圓直徑；kmin,kmax分別為滾子分布系數的最小值和最大值。

為了保證滾子外形的協調，滾子直徑與滾子和軸承滾道的有效接觸長度之間需要滿足：

Ψmin≤Diwe/Liwe≤Ψmax

(12)

式中：Ψmin,Ψmax為比例系數的最小值和最大值；Liwe為滾子接觸長度。

根據赫茲接觸理論，軸承滾子的接觸應力σi可表示為[13-15]：

(13)

式中：Qimax為軸承的最大接觸載荷；E1,E2分別為滾子和套圈的彈性模量；ν1,ν2分別為滾子和套圈的泊松比；Ri1,Ri2分別為滾子和滾道的半徑。

為了避免滾子與滾道之間接觸應力過大而損壞軸承，需要保證接觸應力小于等于其許用值：

σi-[σi]≤0

(14)

式中：[σi]為接觸應力許用值。

根據德國勞埃德船級社風力發電機組認證規范(GL認證)，風機軸承設計壽命至少20 a[12]，因此設計軸承時必須將其壽命作為約束條件。當選擇壽命為優化目標時，表示在滿足許用要求的條件下，壽命最長。

[LA]-LA≤0

(15)

式中：[LA]為壽命許用值。

2.3 設計變量

設計變量是求解優化模型過程中需要優化的參數。由于結構尺寸變量中的自變量能夠引起相關變量的改變，因此將自變量選定為設計變量。

對于CRB，內徑(dc)、外徑(Dc)、內套圈寬度(Tci)、外套圈寬度(Tco)及滾子個數(Zc)能夠確定CRB的其他尺寸變量，因此將這些參數作為自變量。

對于DTRB，內徑(dt)、外徑(Dt)、單列內套圈寬度(Bt)、單列外套圈寬度(Ct)、接觸角(α)、錐角(φ)及滾子個數(Zt)能夠確定DTRB的其他尺寸變量，因此將這些參數作為自變量。

綜上，設計變量X為：

X=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12]=[dc,Dc,Tci,Tco,Zc,dt,Dt,Bt,Ct,α,φ,Zt]

(16)

對于工程類問題，設計過程中需要考慮尺寸參數的范圍。DTRB的接觸角一般為25°左右，因此其定義域為α∈[20°,30°]；取DTRB錐角的定義域為φ∈[1°,4°]；其他變量均為結構尺寸參數，取值范圍均為大于0，計算時可依據外載荷預估給定。

2.4 算法與初始值

優化算法選擇的依據是優化數學模型的類型。本文首先采用目標達到法將多目標優化問題轉換為單目標優化問題，然后采用單目標優化方法進行求解。多目標優化問題轉換后的數學模型為：

(17)

顯然優化數學模型為非線性約束優化問題，序列二次規劃法(SQP)是求解此類問題的有效方法，因此本文選擇此方法。

一般情況下，目標函數具有多個局部最優解，當初始值位于最優解附近時，迭代就能夠收斂。但是在計算時很難直接將初始點設置于最優解附近，因此本文中依據變量的范圍隨機生成初始值。

2.5 結束條件

算法需要滿足設定的結束條件才可以停止迭代。選取以下條件，當迭代滿足任一條件時，算法迭代即停止。

條件1：相鄰冪次兩個變量迭代結果之間的距離滿足允許精度，即

‖Xk+1-Xk‖≤ε1

(18)

式中：Xk+1與Xk為相鄰冪次兩個變量迭代值；ε1為允許精度。

條件2：函數在迭代點處的方向導數滿足允許精度，即

(19)

3 算例分析

已知某型號主軸軸承的設計參數，見表1，要求根據表中的參數設計出軸承結構。

表1 軸承設計參數

依據定義域設置變量的范圍，見表2。

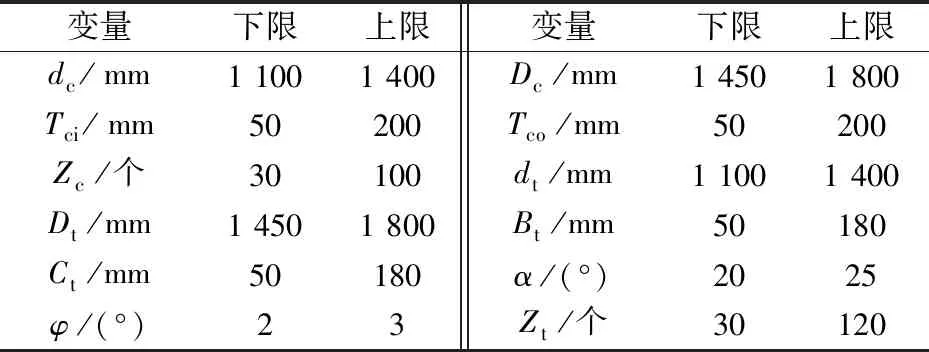
表2 變量范圍

一般情況下，優化目標不同則優化結果不同，分別對單目標與多目標進行優化。借助于MATLAB進行求解，操作流程如圖4所示。

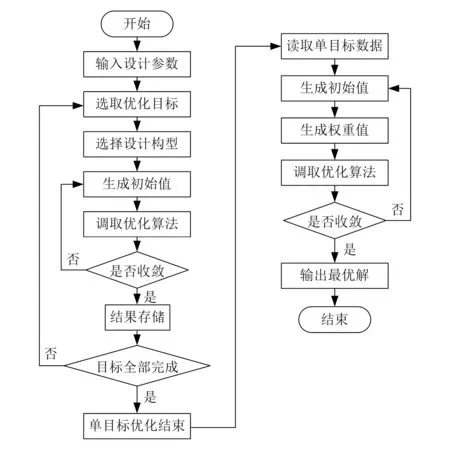
圖4 操作流程圖

對兩種結構軸系的軸承進行單目標優化，優化目標分別為體積和壽命，迭代計算結果見表3。由表中的數據可知，CRB+DTRB軸系結構優于DTRB+CRB軸系結構。

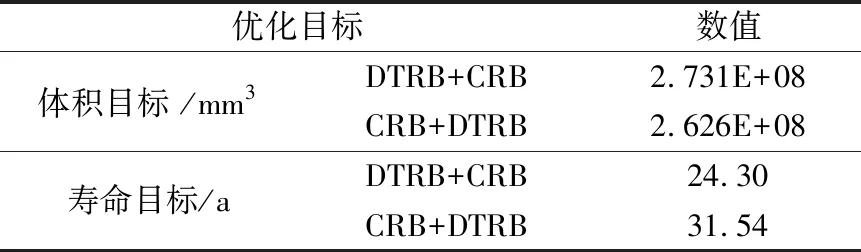
表3 不同結構軸系優化結果

一般在進行多目標優化時，各個目標之間會相互制約，一個目標的最優是以犧牲其他目標為前提，因此多目標優化不可能使所有的目標都得到最優值。以DTRB+CRB軸系結構為例，分別進行單目標優化與多目標優化，優化結果見表4。

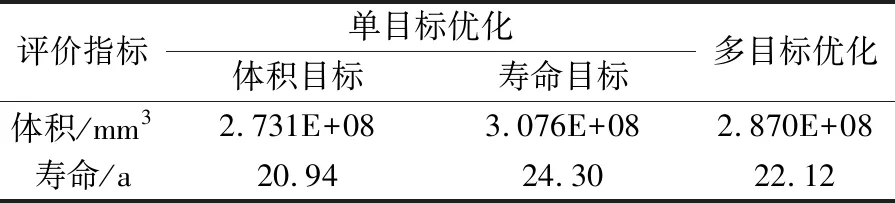
表4 單目標與多目標評價指標結果

由表4可知，多目標優化的結果均介于單目標優化的結果之間，表明多目標優化在迭代計算過程中能夠均衡各個目標。

以DTRB+CRB軸系結構為例，分別對DTRB與CRB進行單獨優化計算，結果見表5。

表5 單獨優化評價指標結果

對比軸系單獨優化與綜合優化結果發現，壽命結果相近，且均能夠滿足許用要求；綜合優化的體積值優于單獨優化的值，表明綜合優化時算法能夠同時迭代優化變量而得到更優的結果。

為驗證使用本文方法得到的軸承的合理性，選取以體積為單目標的DTRB+CRB軸系結構的優化結果，借助RomaxDesigner進行校核驗算，分別得到極限與疲勞載荷作用下的滾子與滾道的接觸應力，如圖5～8所示，圖中數據顯示設計結果滿足要求。

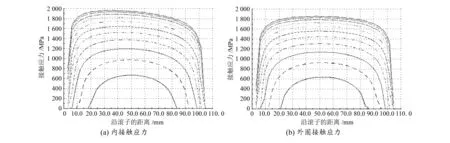
圖5 DTRB極限載荷接觸應力

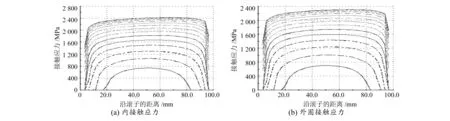
圖6 CRB極限載荷接觸應力

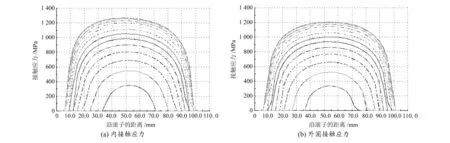
圖7 DTRB疲勞載荷接觸應力

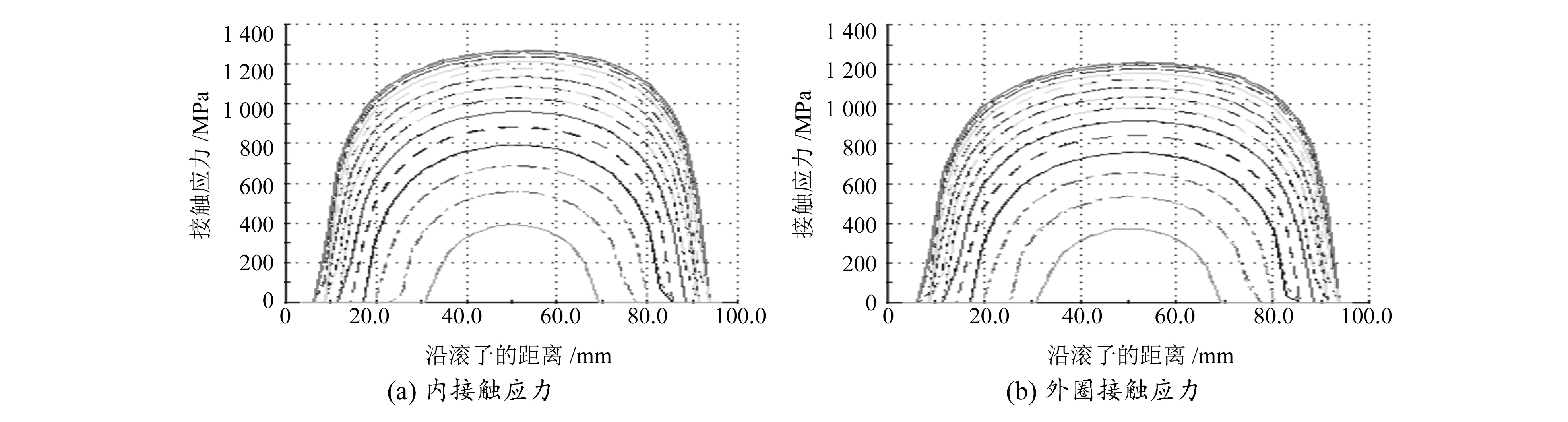
圖8 CRB疲勞載荷接觸應力

4 結論

本文建立了某典型風機主軸系結構的力學模型與優化數學模型，在單目標優化模型的基礎上，耦合出多目標優化模型。以某型號風電機組為例進行優化計算，通過對結果的分析與驗算得到如下結論：

1) 軸系設計時，結構的選擇需要考慮側重于何種優化設計目標，本文以不同優化目標進行優化得到的最優軸系結構均為CRB+DTRB。

2)與單目標優化相比，多目標優化不能保證所有優化目標都能夠達到最優值，但是能夠權衡考慮各個優化目標。

3)相比于對DTRB與CRB單獨優化，對DTRB與CRB進行整體優化能夠綜合考慮兩個軸承而使得結果更均衡、優化目標更優。

4)運用RomaxDesigner對所設計的軸承進行驗證，結果表明軸承設計結果是合理的。