2020年高考全國Ⅰ卷不等式選講試題分析及備考建議

廣東省深圳中學(518001) 周峻民

1 試題呈現

題目(2020年高考全國Ⅰ卷文理第23 題) 已知函數f(x)=|3x+1|-2|x-1|.

(1)畫出y=f(x)的圖像；

(2)求不等式f(x)＞f(x+1)的解集.

該題以分段一次函數的作圖與解不等式為載體,體現數形結合、分類討論、轉化與化歸等數學思想方法,滲透直觀想象、邏輯推理、數學運算等核心素養的考查.

2 試題解答與點評

2.1 試題第(1)問：畫出函數y=f(x)圖像

解由題意知,函數f(x)=函數y=f(x)圖像如圖所示：

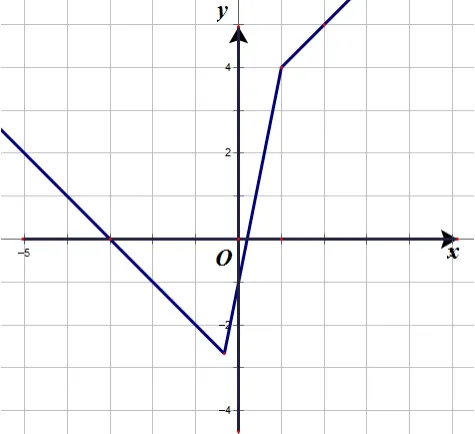
點評本小題設問指向明確,解法單一,通過零點分段法,將含絕對值函數轉化為分段一次函數,再根據各段一次函數的圖像,畫出y=f(x)的圖像.

2.2 試題第(2)問：求不等式f(x)＞f(x+1)的解集

解法1(函數圖像法)將函數y=f(x)的圖像向左平移一個單位長度后得到y=f(x+1)的圖像：

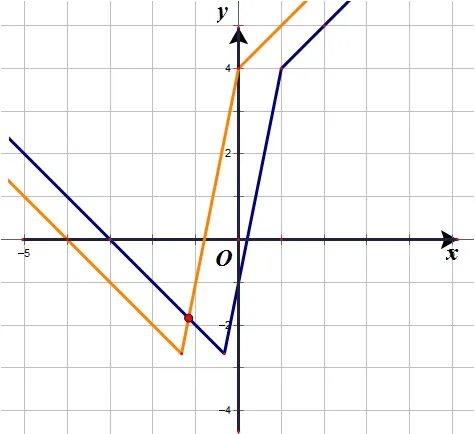
解法2(零點分段法)由題意知f(x+1)=|3x+4|-2|x|,故不等式f(x)＞f(x+1)即為|3x+1|-2|x-1|＞|3x+4|-2|x|.

①當x≤時,-(3x+1)+2(x-1)＞-(3x+4)+2x,即-3＞-4,恒成立,故x≤時原不等式成立；

④當0＜x≤1 時,(3x+1)+2(x-1)＞(3x+4)-2x,即故此時不等式無解；

⑤當x＞1 時,(3x+1)-2(x-1)＞(3x+4)-2x,即3＞4,不成立,故此時不等式無解.

綜上所述,不等式f(x)＞f(x+1) 的解集為

解法3(函數單調性法)由第(1)問y=f(x)的圖像可知,y=f(x)在上單調遞減,在上單調遞增.

①當x＜x+1 ≤即時,y=f(x) 在上單調遞減,從而f(x)＞f(x+1)恒成立,故

綜上所述,f(x)＞f(x+1)的解集為

點評解法1 將不等式問題轉化為函數圖像的交點問題,體現數形結合思想、直觀想象核心素養；解法2 則采用零點分段法去絕對值,直接解不等式,體現了分類討論思想、數學運算核心素養；解法3 則是利用函數單調性這一函數工具處理不等式問題,體現了轉化與化歸思想、邏輯推理核心素養.

3 備考建議

3.1 研究高考,把握方向

下面表1、表2分別是近五年全國卷“不等式選講”的考……