固體炸藥爆轟與惰性介質相互作用的一種擴散界面模型*

于 明

（1. 北京大學應用物理與技術中心，北京 100871；2. 北京應用物理與計算數學研究所計算物理重點實驗室，北京 100083）

爆轟是復雜的流體力學與劇烈的化學動力學耦合的一種物理現象。固體炸藥的爆轟能夠提供強大的能量來驅動和壓縮材料，在國防科技和國民經濟中獲得廣泛應用，因此，固體炸藥爆轟與惰性介質相互作用問題是工程應用中十分重要的問題。固體炸藥爆轟與惰性介質相互作用問題本質上是一種可壓縮多物質流動問題，除了可壓縮單物質流動中出現的激波、稀疏波、接觸間斷外，一種新的間斷，即物質界面出現了，它隔開熱力學性質或狀態方程不一樣的兩種物質，這種物質界面實質上也是一種接觸間斷，它滿足物質界面壓力相等與速度相等的條件。對可壓縮多物質流動，傳統的數值模擬方法多是拉格朗日方法[1-3]，它不能有效地處理物質大變形運動，為了較好地處理物質大變形運動，歐拉方法成為一個很好的選擇[3-4]。根據對處理物質界面的不同方式，歐拉方法大致可以分為4 類：陣面追蹤（front tracking）法[5-6]、流體體積（volume of fluid）法[7-8]、水平集合（level set）法[9-10]以及擴散界面（diffuse interface）法[11-17]等，其中，擴散界面法由于具有邏輯結構簡單、物理量守恒性良好、對界面形狀沒有幾何拓撲限制、對多物理問題適應性較強的特點，近年來獲得了越來越多的關注。

擴散界面法將離散網格視為包含有多種組分物質的混合網格，物質界面被認為是具有一定厚度的虛擬混合區，即把無厚度的物質界面當作有一定厚度的擴散界面，擴散界面內部采用“虛擬狀態方程”或混合規則來描述。根據對多物質混合狀態的不同處理方式，擴散界面模型可以分為兩種[18]：基于單物質流動歐拉方程組的擴展歐拉模型（augmented Euler model）以及基于多相流動Baer-Nunziato 方程組的多相流模型（multiphase flow model）。

在擴展歐拉模型中，混合規則通常采用基于力學平衡和熱學平衡的假設。事實上，熱學平衡僅適用于均勻混合狀況，而包含有物質界面的混合網格內各組分物質通常不是均勻混合的，由此將熱學平衡的假設用于計算包含界面接觸間斷的混合物質的熱力學性質時，往往使得物質界面附近的壓力和速度等物理量出現非物理振蕩現象[19]。為了消除物質界面附近的非物理振蕩現象，不得不采取另外的技術方案進行修正處理，如附加狀態方程參數演化方程[20]、總能量調整[21]、守恒與原始變量轉換[22]等。

不同于擴展歐拉模型，多相流模型[23]中的混合物質被認為由處于熱學、力學、化學非平衡的多種組分物質組成，每種組分物質具有各自的物理狀態并按照各自的動力學規律分別進行演化，演化方程含有用于表達由組分物質非平衡引起的質量、動量和能量相互轉化的各種源項，同時采用組分物質體積分數方程來描述物質界面的運動過程。由于考慮了每種組分物質各自的變化規律，能夠保證混合物質的熱力學性質自動滿足一致性，從物理建模上消除了物質界面附近的非物理振蕩，對諸如爆轟這種帶有化學非平衡的可壓縮流動，消除物質界面附近的非物理壓力振蕩非常重要，因為爆轟化學反應的激發與壓力等量密切相關，如果壓力出現非物理振蕩會激發虛假的化學反應，進一步會引起錯誤的爆轟特性。針對具體物理過程，熱學、力學、化學非平衡這些狀態可以全部滿足也可以部分滿足，在全部滿足非平衡條件下即為著名的Baer-Nunziato 模型，在部分滿足非平衡條件下形成各種簡化多相流模型，如在力學平衡、熱學非平衡條件下有Kapila 模型[24]、Allaire 模型[25]、Massoni 模型[26]、Murrone 模型[27]、Grove 模型[28]等多種典型模型，這些不同模型的差異主要在于以不同方式處理組分物質混合狀態，使得組分物質體積分數方程有不同的表達形式。多相流模型由于考慮了更精確的物理機制，更加符合物理意義，近年來在可壓縮多物質流動數值模擬領域獲得了極大的重視，本文的工作正是基于多相流模型。

在固體炸藥爆轟與惰性介質的相互作用過程中，爆轟化學反應過程通常簡化為固相反應物轉化成氣相生成物，這樣組分混合物質通常包括固相反應物、氣相生成物、惰性介質這3 種成分，由于這3 種組分物質的材料物態性質和熱力學性質差異極大，因此它們之間的相互作用過程被認為滿足力學平衡和熱學非平衡狀態[13,24,29]，即在流場控制體中每種組分物質擁有相同的壓力和速度、以及不同的溫度和內能。基于多相流思想，固體炸藥爆轟與惰性介質相互作用過程首先由各種組分物質的質量守恒方程、混合物質的動量與總能量守恒方程描述，組分物質的質量守恒方程還需考慮由化學反應引起的質量轉化的影響，然后需要補充每種組分物質的體積分數的控制方程。由混合物質能量守恒方程可以分解獲得每種組分物質的內能變化方程，再利用每種組分物質壓力相等的條件并結合組分物質的質量守恒方程，可以推導出每種組分物質的體積分數控制方程。由于涉及到熱學非平衡狀態，組分物質之間存在熱量交換，分解獲得的組分物質內能變化方程還需考慮熱量交換的影響。這樣，推導出的組分物質體積分數控制方程同時包含了化學反應和熱學非平衡的影響。并且，混合物質的壓力演化方程也被納入到模型方程組中，這樣壓力通過直接離散求解演化方程獲得而不是由流動守恒變量計算獲得，這種方案可以增強消除物質界面非物理振蕩的效果，也可以避免由狀態方程非線性形式引起的壓力迭代求解[28]或者由組分體積方程非守恒型引起的壓力松弛求解[13]，還可以避免計算壓力對守恒變量的導數而簡化高階精度格式的運算過程。最終，獲得的擴散界面模型方程組包括組分物質的質量守恒方程、混合物質的動量及總能量守恒方程、組分物質的體積分數演化方程以及混合物質的壓力演化方程。獲得的擴散界面模型的最主要特點是考慮了化學反應以及熱學非平衡的影響，因此具有良好的熱力學一致性，同時，該擴散界面模型能夠適用于任意表達形式的狀態方程以及任意數目的多種惰性介質。

對所獲得的擴散界面模型方程組采用一個具有波傳播性質的時空二階精度的有限體積法進行數值求解，典型算例結果顯示，數值模擬圖像與物理規律符合，物質界面附近不會出現物理量的非物理振蕩現象。

1 擴散界面模型的推導

首先給出物理量的定義。考慮一個控制體包含有炸藥固相反應物、炸藥氣相生成物以及惰性物質，固相反應物的物理量用下標s 表示、氣相生成物的物理量用下標g 表示，惰性物質設有K種物質，每種物質的物理量用下標k表示；其中 ρ 表示密度，e表示內能，p表示壓力，u表示速度矢量， α 表示體積分數，v表示比容，Q表示單位質量的固體炸藥由固相反應物轉化為氣相生成物時所釋放的熱量。在力學平衡條件下，混合物質物理量與組分物質物理量的關系式為：

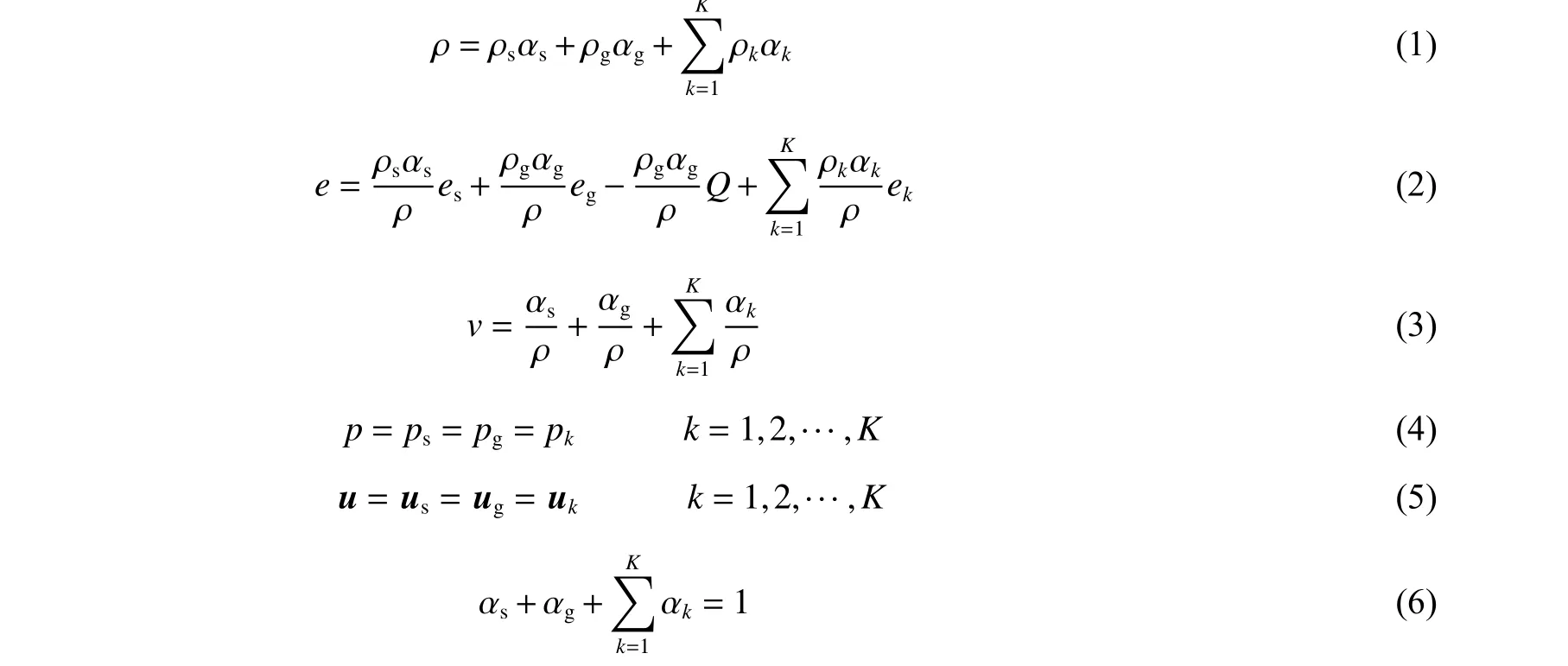
不考慮各種耗散因素及外力做功情況，則在力學平衡狀態條件下固體炸藥爆轟與惰性介質的可壓縮流動方程組可以表達為：

式(7)為固體炸藥固相反應物的質量守恒方程，式(8)為固體炸藥氣相生成物的質量守恒方程，式(9)為惰性介質的質量守恒方程，式(10)為混合物質的動量守恒方程，式(11)為混合物質的總能量守恒方程。

在給定每種組分物質的狀態方程條件下，并確定了每種組分物質的體積分數的控制方程之后，上述流動方程組成為封閉系統進而可以獲得定解。組分物質體積分數的控制方程可由混合物質的能量守恒方程并結合混合網格內每種組分物質壓力相等的條件導出，混合物質的能量守恒方程可以分解為每種組分物質的內能變化方程。

上述流動方程組式(7)～(11)可以經過變換得到混合物質的內能守恒方程：

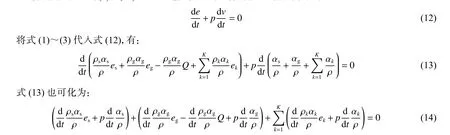
式(14)中3 個括號中分別表示炸藥固相反應物、炸藥氣相生成物、惰性介質的內能變化，再考慮到這多種物質由于處于熱學非平衡狀態而存在溫度差異，物質之間會產生熱量交換，則可以將式(14)分裂為各種組分物質的內能變化方程：

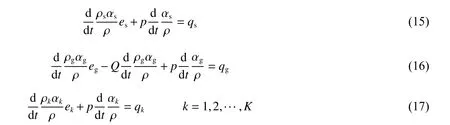
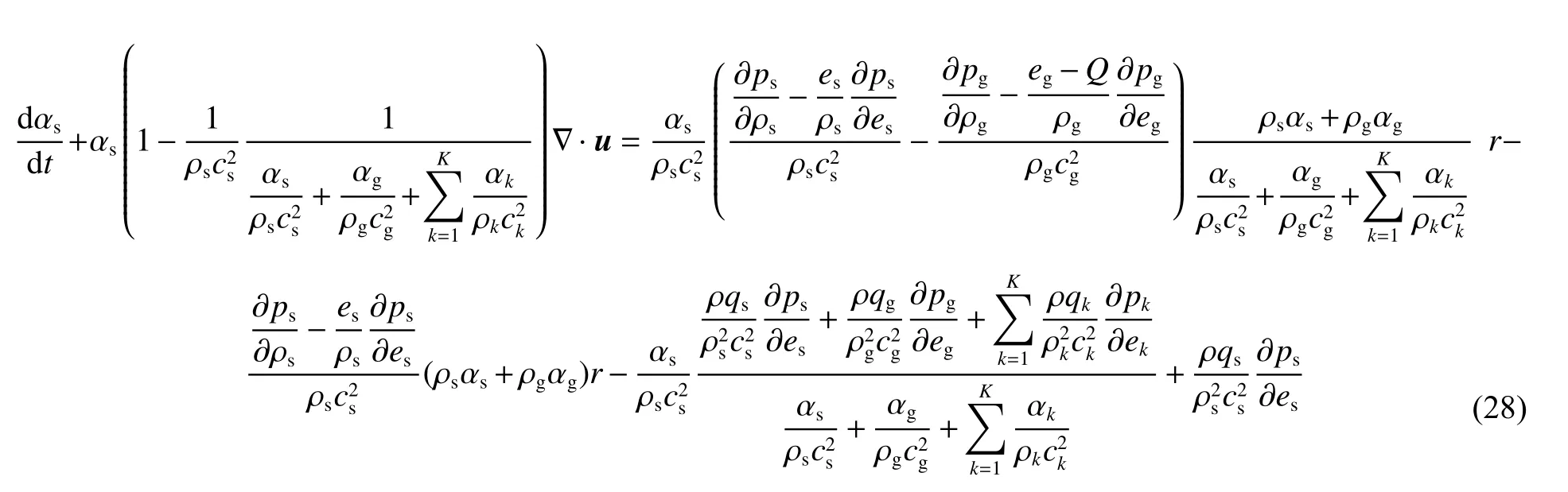
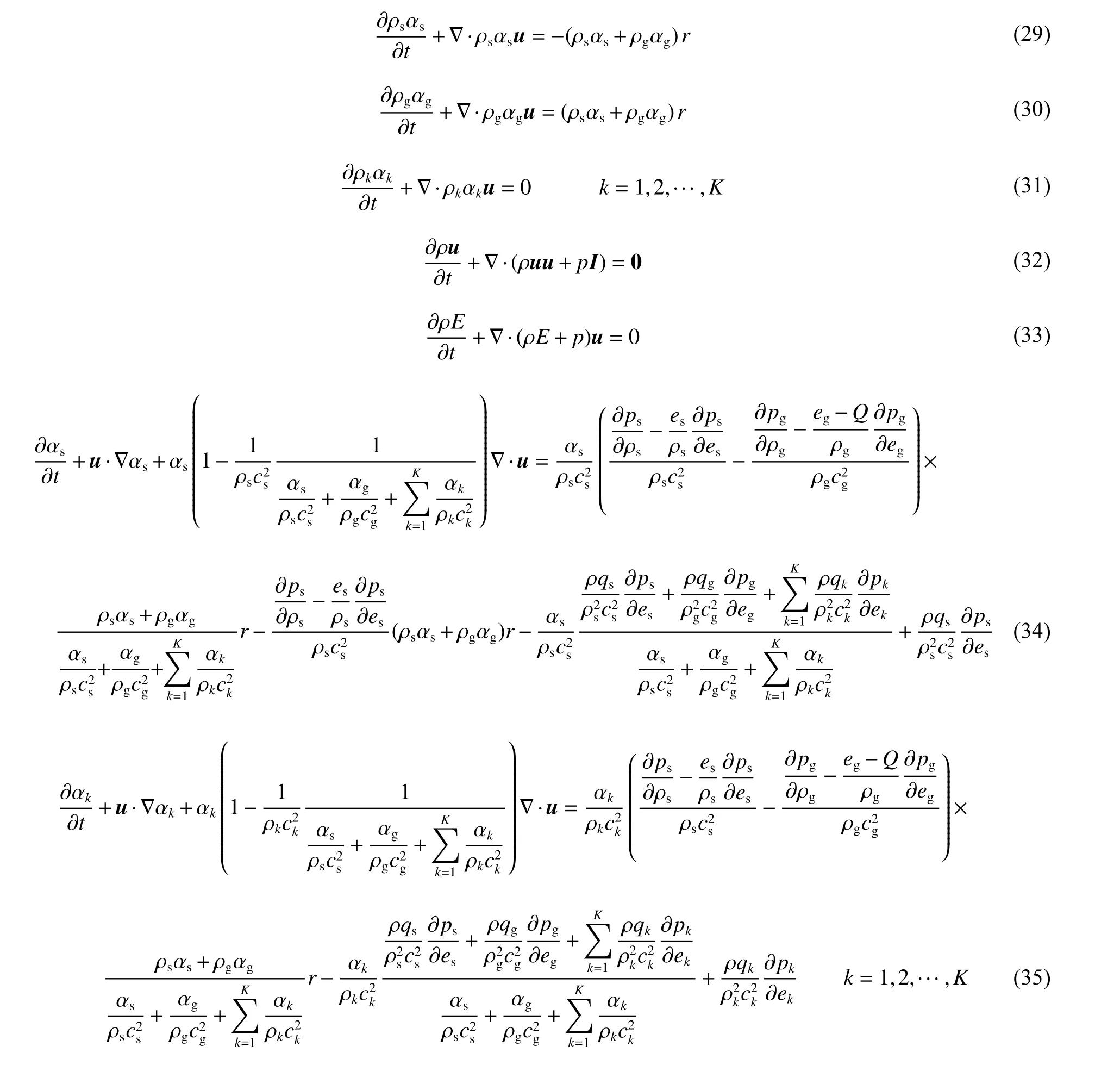
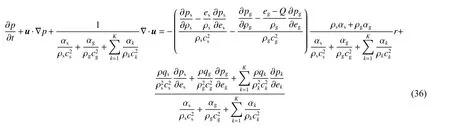
同理可以得到氣相生成物與惰性介質的體積分數控制方程，這樣各組分物質的體積分數控制方程均可獲得，同時，混合物質的壓力演化方程也成為一個流動控制方程，這樣固體炸藥爆轟與惰性介質相互作用的擴散界面模型被推導出：

2 數值方法

為了便于數值求解，獲得的界面擴散模型方程組(29)～(36)在二維直角坐標系下可以寫成如下矢量-矩陣形式的偏微分方程組：

這里狀態變量q=[ρsαs, ρgαg, ρkαk, ρu, ρv, ρE, αs, αk,p]T（不失一般性，惰性介質只寫一種物質），矩陣A(q) 與矩陣B(q) 是具有類似表達形式的Jacobi 矩陣，其中

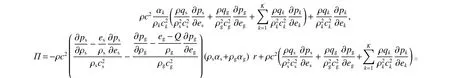
非齊次非守恒型雙曲律方程組(30)可用Strang 分裂方法[30]來求解，求解過程依次為雙曲律方程組求解步與常微分方程組求解步。在雙曲律方程組求解步中，一個具有波傳播特征的二階精度Godunov型格式[31]被采用，該格式能夠很好地處理雙曲律方程組中的非守恒型對流項。在常微分方程組求解步中，首先根據固體炸藥爆轟通常具有快反應過程和慢反應過程的特點[29]，將爆轟化學反應率分解成快反應率和慢反應率兩部分，然后一個具有顯-隱離散特性的二階精度Runge-Kutta 格式[32]被采用，顯式離散用于處理慢反應率源項、隱式離散用于處理快反應率源項。

3 典型算例

3.1 一維爆轟增長問題

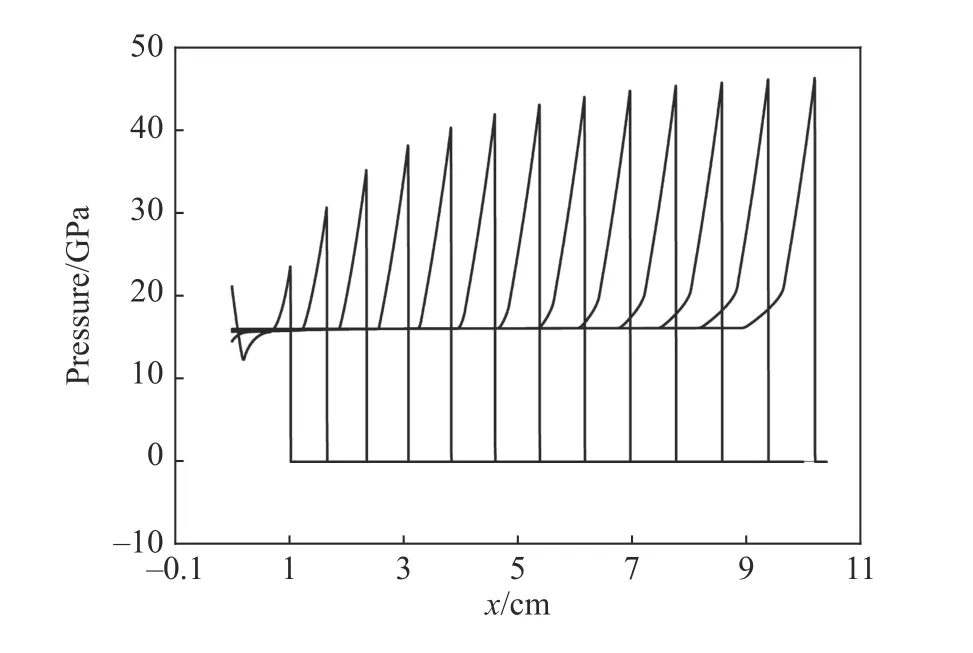
圖1 一維爆轟的壓力增長過程Fig. 1 Growth of pressure in one-dimensional detonation

3.2 滑移爆轟約束效應問題

考察一平面爆轟在金屬銅的約束下向前傳播情況，計算域如圖2 所示，固體炸藥固相反應物和氣相生成物均采用Jones-Wilkins-Lee 形式狀態方程[34]；爆轟化學反應率采用Ignition-Growth 模型[34]；銅采用Mie-Grüneisen 形式狀態方程[18]。起爆區域設置有壓力為36.5 GPa 的高壓靜止氣相生成物，其余區域均設置為標準狀態；計算域入口設置為定值，其余邊界設置為無反射邊界條件。

圖2 滑移爆轟約束構型圖Fig. 2 Configuration of confinement effect

計算獲得爆轟波達到定常狀態時的密度及壓力的分布，如圖3 所示，可以看出，炸藥與銅界面附近的爆轟波陣面呈彎曲狀態，爆轟波向銅介質折射一激波。數值計算獲得定常爆轟狀態下炸藥與銅界面附近的爆轟波陣面的形態，如圖4 所示，爆轟定常傳播速度計算值為7 670 m/s（理論值為7 655 m/s）；爆轟波陣面邊緣角 α 的計算值為81.3°（理論值為78.8°），偏轉角 θ 的計算值為4.86°（理論值為4.75°），計算結果與理論結果吻合較好。同時也可以看出，爆轟波向金屬進行的折射為正規折射，界面處沒有出現反射波。

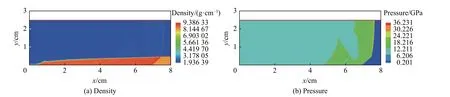
圖3 銅約束爆轟波傳播的密度及壓力分布Fig. 3 Distribution of density and pressure in detonation flowfield under copper confinement

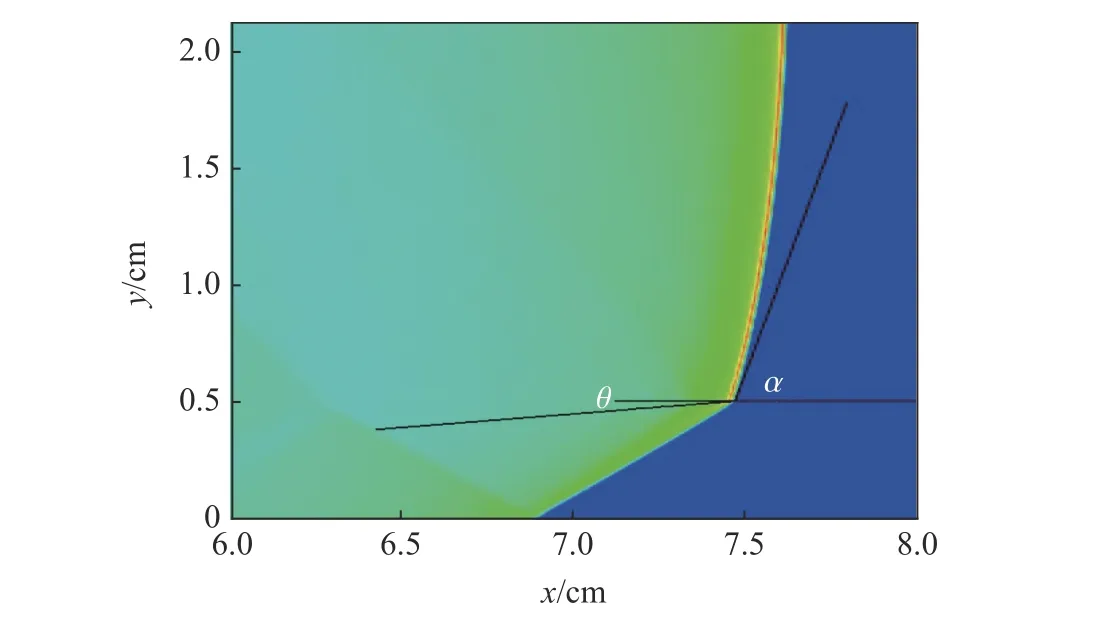
圖4 銅約束下爆轟波陣面形態Fig. 4 Detonation flowfield nearby explosives under copper confinement

3.3 平面爆轟波繞射問題

定常的平面爆轟波繞一個由金屬銅構成的90°擴張通道進行傳播，計算域如圖5 所示。固體炸藥固相反應物和氣相生成物均采用Jones-Wilkins-Lee 形式狀態方程[34]；爆轟化學反應率采用Ignition-Growth 模型[34]；銅采用Mie-Grüneisen 形式狀態方程[18]。起爆區域設置有壓力為36.5 GPa 的高壓靜止氣相生成物，其余均為標準狀態；計算域入口設置為定值，上邊界設置為固壁條件，其余邊界設置為無反射邊界條件。

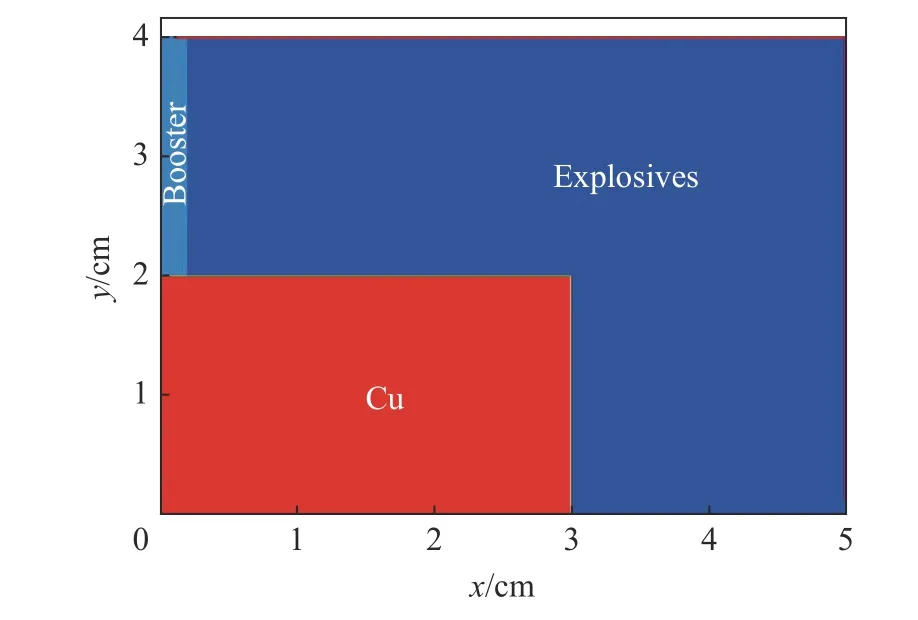
圖5 爆轟波繞射構型圖Fig. 5 The configuration for the diffraction of detonation wave

計算獲得爆轟波在t= 4.25，5.00，5.75，6.50 μs 這4 個時刻的密度和壓力分布，如圖6 所示。

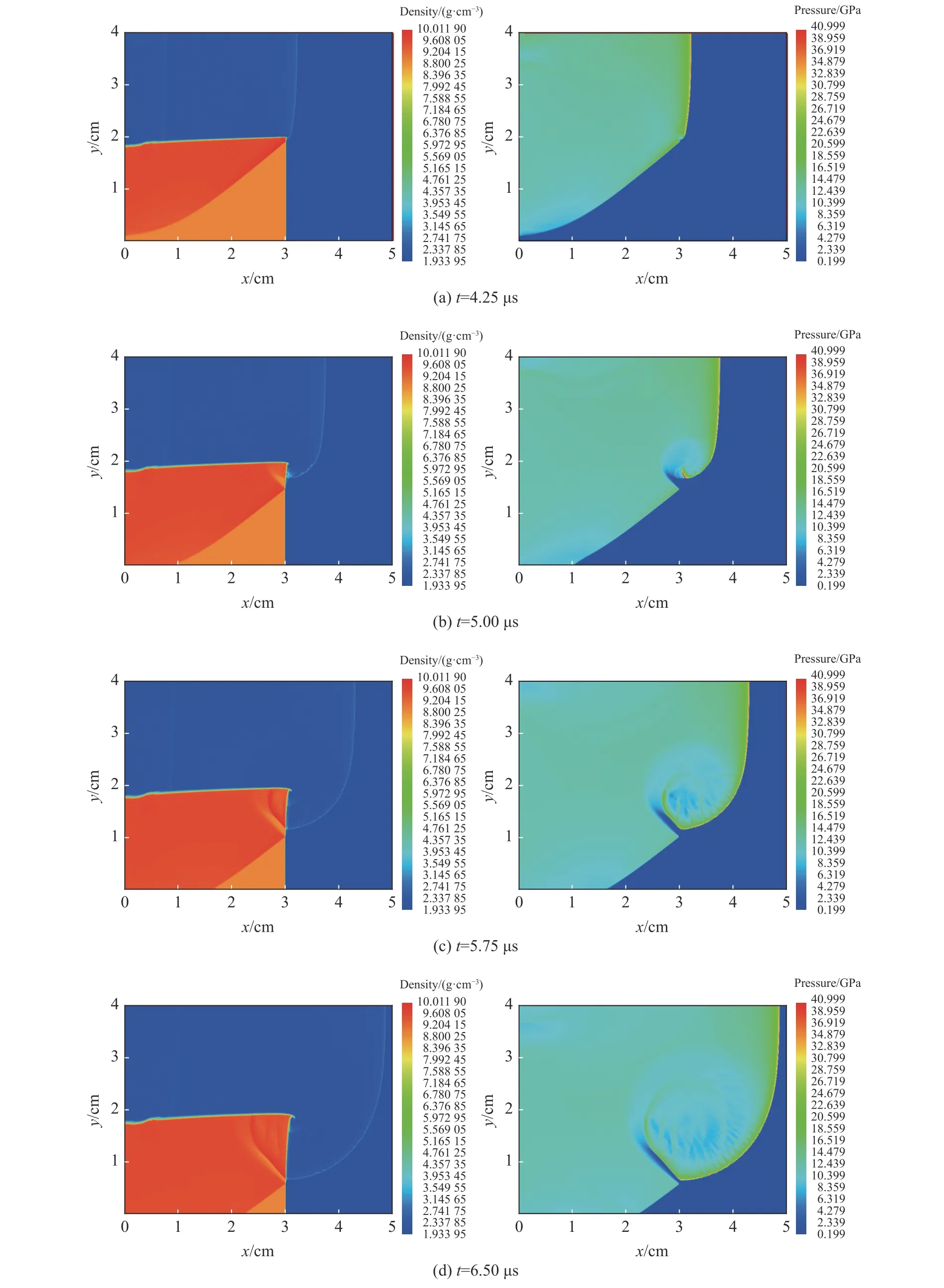
圖6 爆轟波繞射流場圖Fig. 6 The flowfield for the diffraction of detonation wave at various simulation times

從密度圖看，爆轟波在銅介質中產生正規折射激波，該折射激波跨過臺階時會預壓炸藥；從壓力圖看，銅介質中折射激波在向炸藥折射過程中產生稀疏波引起銅介質出現一個低壓區。

4 結 論

本文中提出一種具有熱力學一致性的數值模擬固體炸藥爆轟與惰性介質相互作用的擴散界面模型，該模型基于混合網格內各組分物質處于力學平衡與熱學非平衡假設，推導獲得的模型流動控制系統包括組分物質的質量守恒方程、混合物質的動量及總能量守恒方程，以及組分物質的體積分數演化方程和混合物質的壓力演化方程。典型算例表明，數值計算結果與物理規律符合，并且在物質界面附近不會出現物理量的非物理振蕩現象、適用于任意表達形式的物質狀態方程以及任意數目的惰性介質。