地鐵隧道毫秒延時爆破環境振動特性研究*

趙 凱，趙丁鳳，張 東，莊海洋，陳國興

（1. 南京工業大學巖土工程研究所，江蘇 南京 210009；2. 中交上海航道勘察設計研究院有限公司，上海 200120；3. 中設設計集團股份有限公司，江蘇 南京 210014）

隨著城市地鐵的發展，隧道爆破掘進穿越堅硬巖土層的案例屢見不鮮[1-2]，但由于地鐵沿線建筑林立、地下管線密布，隧道施工過程中爆破誘發的環境振動效應成為了該工程領域研究的重點和難點。爆破振動強度過大導致圍巖破壞[3-4]、爆破引起建筑物共振以及高頻爆破振動迫使剛性結構產生局部應力集中[5]，均可能導致爆破影響區內的構筑物產生不同程度的損傷。為減振降害，通過電子雷管或非電雷管精確控制多孔毫秒延時爆破，既能顯著改善巖石破碎效果，又能有效減小爆破振動[6]。不少學者從大量的爆破資料中總結出毫秒延時爆破的工程參數[7-8]，如毫秒延時爆破最佳間隔時間[9]、最優單孔藥量以及爆破順序[10]等。然而，由于實際工程地質條件千差萬別[11]，此類現場爆破試驗往往具有較強的地域性，且現場試驗前單孔藥量及爆破順序等設計參數尚不明確，容易導致相鄰建筑物損傷。因此，合理有效的數值模擬成了較理想的預測爆破效果和確定爆破參數的方法[12]。然而，由于延時爆破中各起爆點的單孔裝藥量不同，爆破荷載不規則，而常規的數值模擬較難反映此類不規則爆破荷載作用下巖土材料的動力響應特征。

針對上述問題，本文中基于南京地鐵隧道毫秒延時爆破環境振動特性現場試驗，首先建立有限元-無限元耦合邊界的地層-爆源體系的三維精細化有限元模型。其中，考慮爆破荷載的不規則特性，采用基于非對稱加卸載準則修正的Davidenkov 本構模型描述場地土體的動力非線性特性；通過改進的Friedlander 方程來模擬內源爆炸在圓柱形炮孔表面產生的瞬態空氣沖擊波。通過與已開展現場爆破試驗的實測數據進行對比，驗證該模型方法的有效性。最后，對齊爆和毫秒延時爆破的峰值振速及頻譜特性進行對比，探討毫秒延時爆破環境振動特性及減振機理。

1 現場爆破試驗回顧

1.1 工程背景

南京地鐵四號線云南路～鼓樓站區間全長約660 m，擬采用礦山法施工，包括區間隧道、風道、鼓樓小里程暗挖段和三聯拱部分。鼓樓站東側為既有地鐵一號線鼓樓站，東側有已通車的鼓樓隧道，西側為鼓樓公園，公園環島中間為文物古建筑。區間隧道距鼓樓城闕僅約1.3 m，豎向距離14.5 m；1#風道距城闕約為19.8 m，豎向距離13.5 m；三聯拱距城闕約為18.1 m，豎向距離11.0 m，暗挖結構與文物鼓樓的相對位置如圖1 所示。

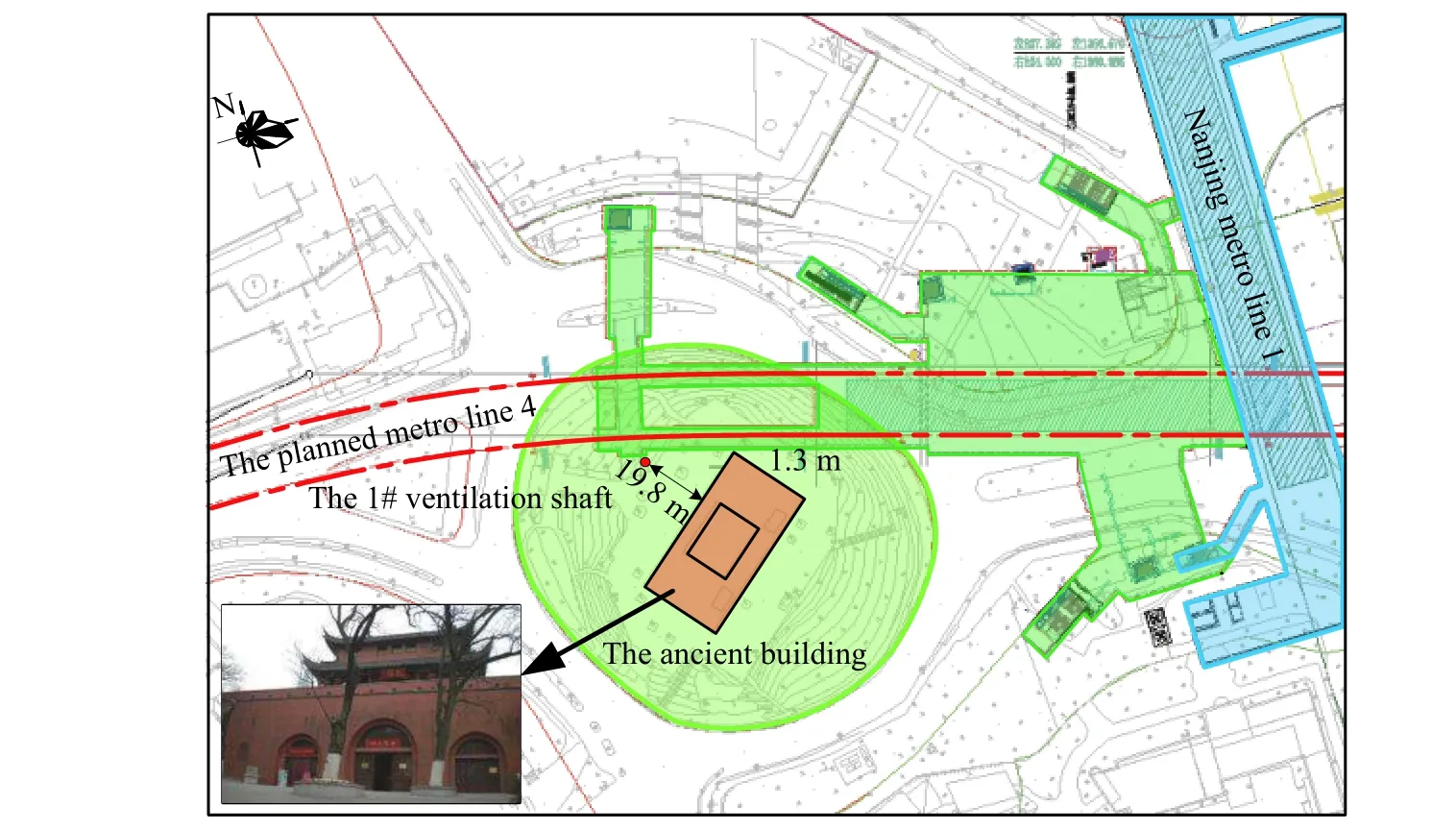
圖1 地鐵隧道與文物鼓樓的相對位置Fig. 1 Relative position between the metro tunnel and the cultural relic drum tower

1.2 現場爆破試驗方案

由調查可知，文物鼓樓的病害較嚴重，且區間隧道距鼓樓城闕水平距離最近僅約1.3 m，為避免直接近區爆破對文物鼓樓的安全性產生影響，在文物鼓樓周邊選取了爆破試驗區域。爆破試驗前，采用環境隨機激振法（也稱脈動法）對鼓樓的固有頻率進行測試，結果列于表1。

結合現場實際情況和勘查資料（見圖2）可知，1#風道位于K-3-2 及K-3-3 中風化砂礫巖層，該區域地質情況與文物鼓樓處較接近，因此將隧道1#風道作為模擬爆破點。此外，區域場地構成上軟下硬軟硬不均的工作面，相對于單純的巖體，巖石-土軟硬交界面的存在將放大爆破引起的地表峰值振速，也將間接影響文物鼓樓的峰值振速。預先在掌子面掏槽，形成臨空面，掘進進尺為0.6 m，鉆孔孔深取0.7 m，炮孔孔徑為42 mm，炮孔距取0.5 m。試爆分為二類，共進行了6 次爆破測試。一類為單孔按順序爆破，相互之間沒有干擾，1～5 號孔單孔藥量依次為100、200、300、400、500 g，共5 種工況；二類為六孔毫秒延時爆破，其中6～10 號孔每孔裝藥200 g，11 號孔裝藥100 g，共1 100 g，各孔間延時50 ms。模擬爆破作業在K-3-2 層的中風化砂礫巖中，圍巖等級為Ⅱ～Ⅳ的堅硬巖石，如圖2 所示。

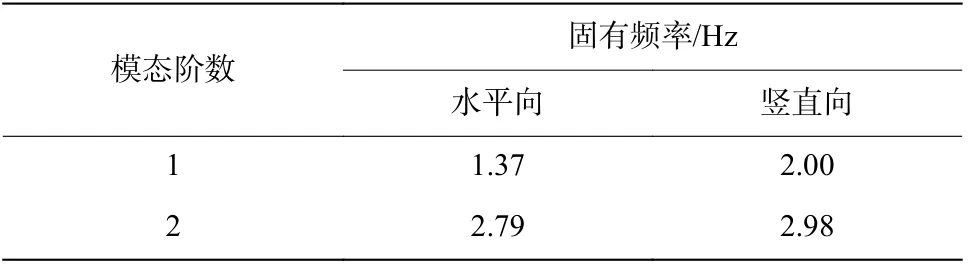
表1 鼓樓固有頻率測試結果Table 1 Test results of natural frequencies of the drum tower

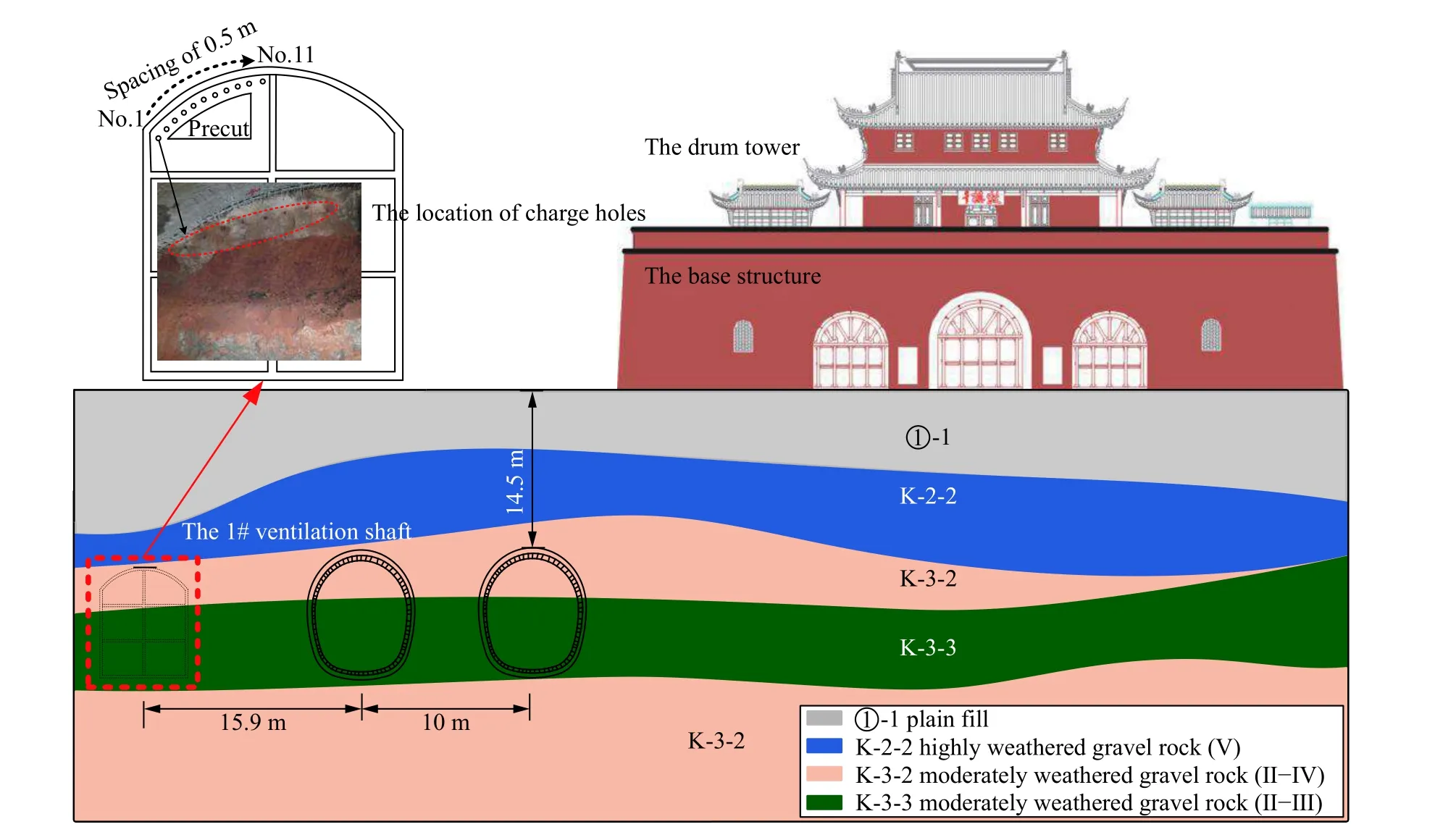
圖2 鼓樓與模擬爆破點的相對位置及地層分布Fig. 2 Relative position between the drum tower and the blasting site as well as stratum distribution

2 土體動力本構模型

采用非線性滯回本構模型描述巖土體對爆破振動波的能量耗散作用[13]。為更好地描述并簡化不規則荷載作用下Davidenkov 模型的剪應力-剪應變關系曲線，趙丁鳳等[14]引入Pyke 的n倍法對加卸載準則進行修正（見圖3），當施加的應力轉向后，后續的剪應力-剪應變曲線沿當前拐點指向歷史上最大（小）點的方向前行，此時循環剪應力 τ -剪應變 γ 關系由以下公式來描述：

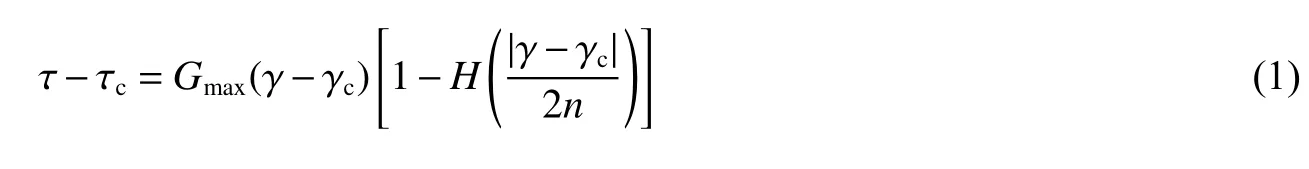
式中：Gmax=ρv2s為最大剪切模量， ρ 為土體密度，vs為土體剪切波速； τc和 γc分別為加卸載轉折點處的剪應力和剪應變。

通過對式（1）中的變量( γ ?γc)求導，得到應力-應變滯回曲線段t時刻的時變切線剪切模量的表達式：

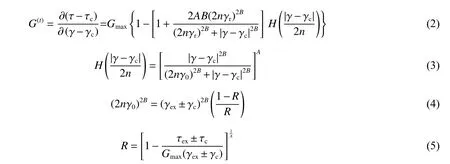
式中：A、B和 γ0為土的試驗參數； τex和 γex分別為歷史上的最大剪應力和剪應變；符號“±”在加載時取“?”，卸載時取“+”。

根據上述修正，除記錄歷史上最值點外，當施加的應力轉向后，只需要記憶當前轉折點處的應力和應變，就可以確定應力-應變曲線的走向，通過這樣的方法可以有效解決轉折點信息記憶量大的問題[14]。此時，不規則加卸載條件下的應力-應變路徑為曲線段 0→1→2→3→4→5→6→7，修正2 倍Masing 法則中的曲線段2→1→3 或曲線段6→5→7，模型參數見表2。

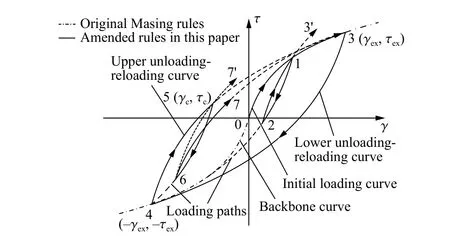
圖3 不規則加卸載準則修正的Davidenkov 模型[14]Fig. 3 The Davidenkov model modified by the irregular loading-unloading rules[14]

表2 土體剖面及Davidenkov 模型參數Table 2 Parameters for the soil profiles and the Davidenkov model

3 三維數值模型的建立

3.1 毫秒延時爆破荷載輸入

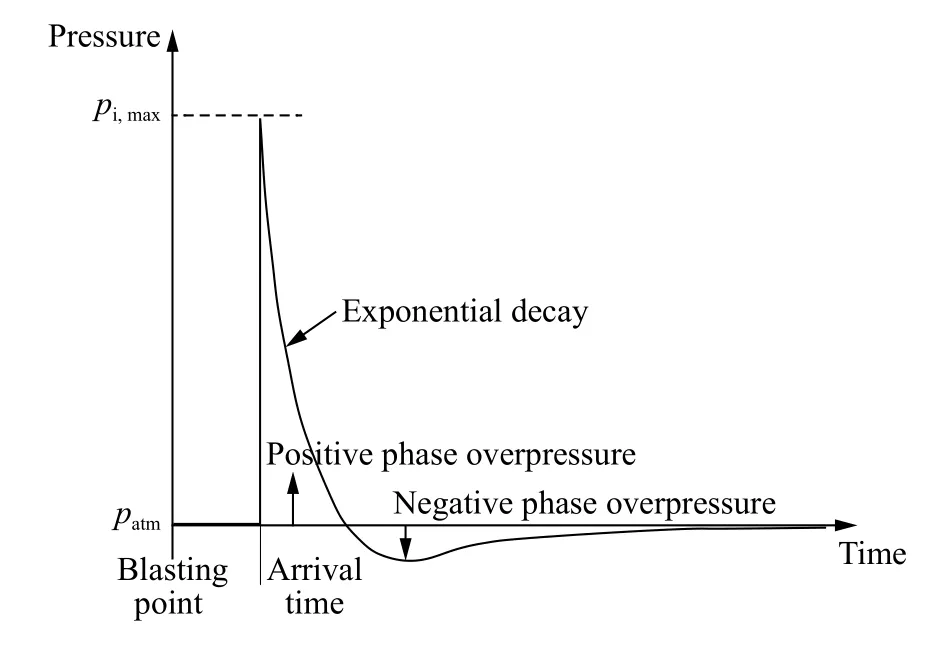
圖4 爆炸引起的超壓時程曲線Fig. 4 Time history of overpressure induced by blasting

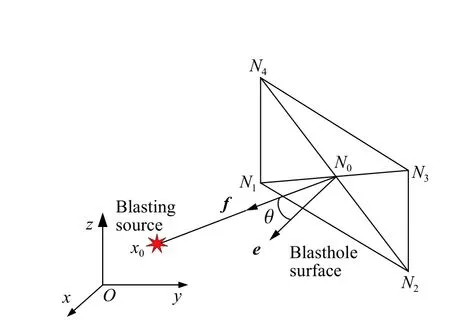
圖5 爆炸沖擊波至炮孔表面的入射角度Fig. 5 Illustration of the incident angle of the blast wave to the surface of the blast hole

ConWep 模型參數涉及爆源至迎爆面的距離、裝藥量和起爆時刻等。相比于直接施加半理論半經驗的爆破荷載壓力時程曲線，ConWep 模型中考慮了爆破沖擊波入射壓強和反射壓強在炮孔表面的空間耦合效應，增加了空間維度。

3.2 地層-爆源體系三維有限元模型

爆破是一個非常復雜的力學過程，現有的有限元、離散元等數值方法難以準確模擬炮孔起爆條件下從炸藥爆轟、巖石破碎到彈性地震波激發這一復雜過程，需尋求一種實用的等效模擬方法。本文中采用等效彈性邊界的概念[16-19]，把炮孔周圍巖體根據其破壞程度劃分為粉碎區、破碎區和彈性振動區，將整個非彈性區(粉碎區和破碎區)等效為爆炸源，由ConWep 模塊激發的爆炸沖擊波直接作用在等效彈性邊界上，產生隨時間和空間變化的壓強。

考慮到圓柱形炮孔能量傳播的三維特性，基于ABAQUS 平行計算平臺，建立了三維有限元精細化模型。炮孔等效彈性邊界按照文獻[16-19]近似取值r=10r0(r0為實際孔徑)。爆源設置在炮孔中心處，由ConWep 模塊施加在炮孔等效彈性邊界上。計算區域為75 m×83 m×20 m。為彌補有限元模型中場地尺寸過大對計算效率的影響，模型邊界采用有限元-無限元耦合的方法來模擬，以考慮爆破地震波在邊界的透射問題。模型除自由表面及炮孔所在面外，均設置為無限單元，炮孔所在面約束法向位移。計算采用單元總數8 009 728 個，具體三維有限元模型如圖6 所示。

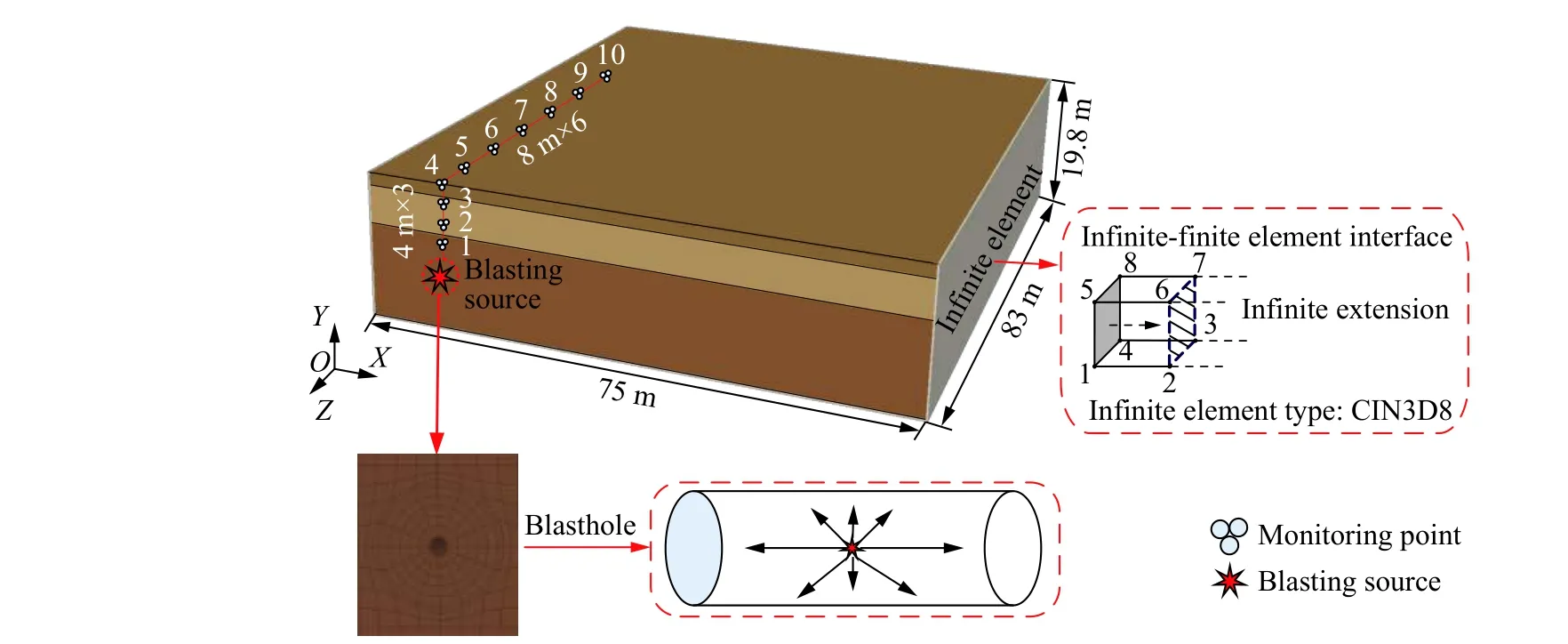
圖6 地層-爆源體系三維有限元模型Fig. 6 A three-dimensional finite element model of the ground-blasting-source system

4 數值模擬與實測結果的對比

為初步驗證此次建立的模型對大型場地爆破地震波傳播規律的預測能力，現對比現場爆破試驗與數值模擬得到的地表振動響應。圖7 對比了地表試驗測點（橫坐標）與數值模擬（縱坐標）所得的豎直向/水平向峰值振動速度。由圖7 可知，無論是豎直向峰值振動速度，還是水平向峰值振動速度，兩者的實測值與模擬值較均勻地分布在45°線附近。這表明，基于修正的Davidenkov 本構模型以及改進的Friedlander 方程的三維精細化有限元模型能較真實地反映爆破試驗場地的地表振動特性。

圖8 對比了測點5 (距爆源水平距離8 m 處) 和測點9 (距爆源水平距離40 m 處) 地表水平振動速度時程和傅里葉譜的模擬與實測結果。整體而言，模擬與實測的振動速度衰減規律較一致，遠處測點的實測速度時程稍有滯后，這是由于實際場地中土的阻尼特性更顯著。此外，對比這兩個測點速度響應的傅里葉譜可知，模擬與實測速度響應的頻譜成分、譜形及譜值基本相同。綜上可知，本文模型方法能較理想地模擬爆破荷載作用下場地的環境振動特性，反映爆破地震波在場地傳播過程中的耗能特性。

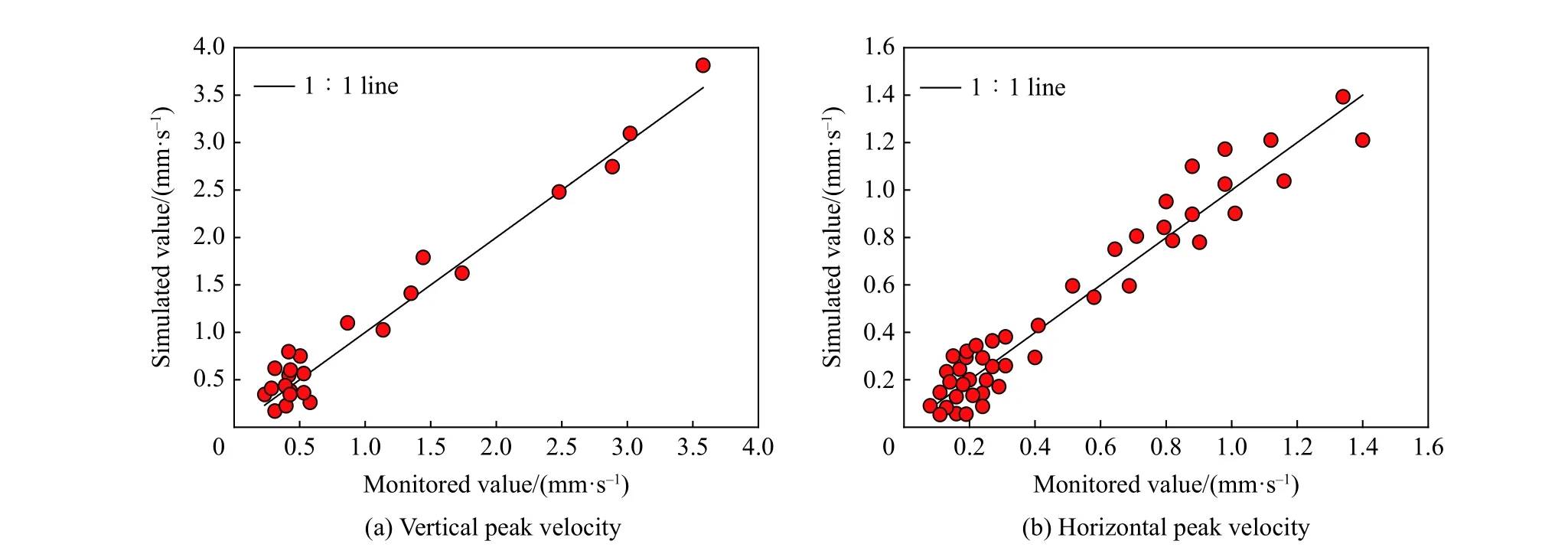
圖7 實測地表測點峰值振速與模擬結果的對比Fig. 7 Comparison of peak vibration velocities between monitoredand simulated surface measurement points

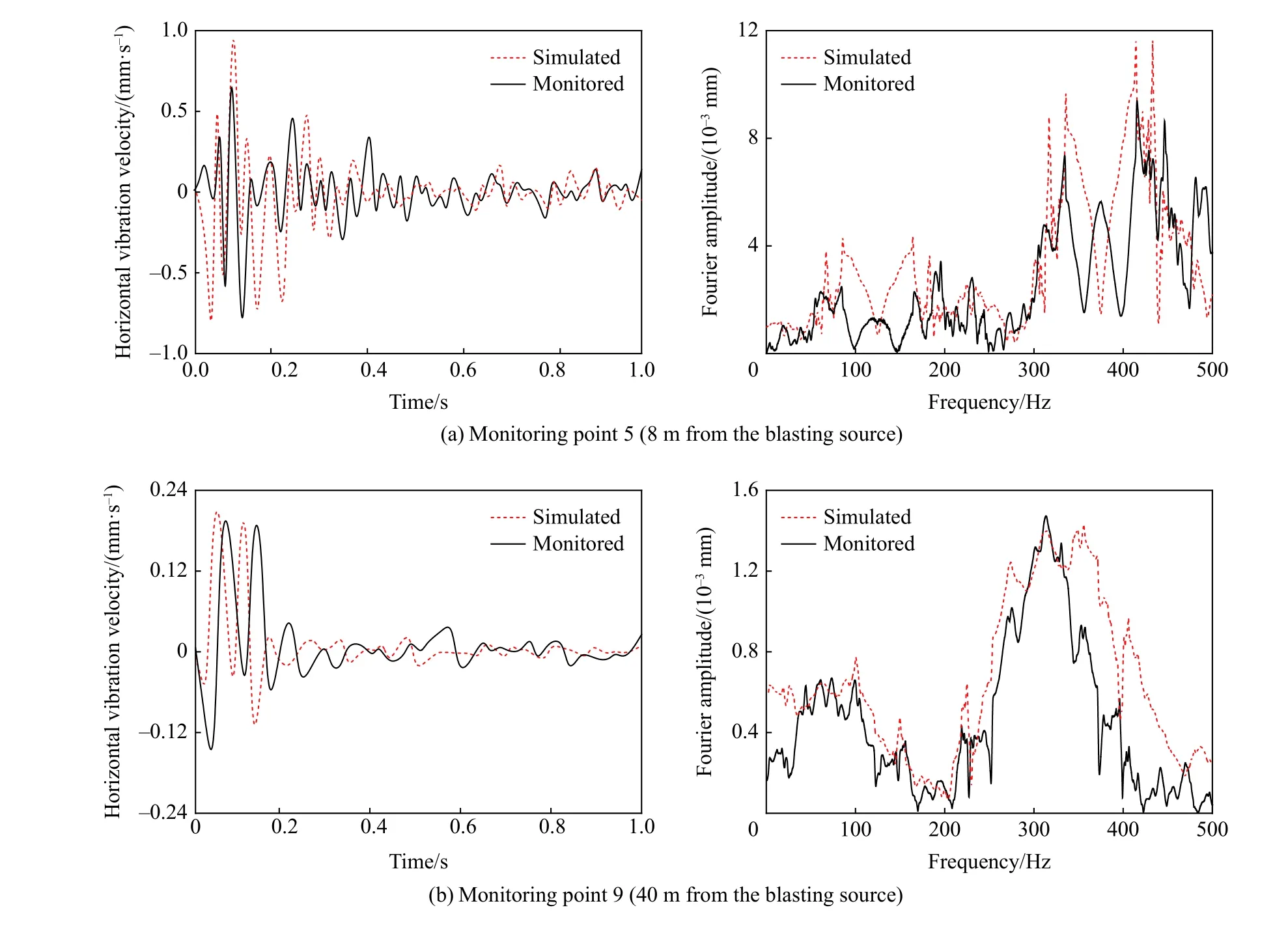
圖8 地表振動速度時程和傅里葉譜對比Fig. 8 Comparison of vibration waveforms and Fourier spectra bewteen different monitoring points

5 爆破模式對地表速度響應的影響

由于巖土體的阻尼特性，隨著傳播距離的增大，爆破地震動的能量在巖土介質不斷耗散。此外，場地反應也與爆破地震動的特性密切相關。因此，了解不同爆破模式對場地地表響應的影響機理，有利于爆破方案的合理設計。對此，開展了兩種爆破方案的數值計算：(1)六孔齊爆，單孔裝藥量為500 g；(2) 六孔毫秒延時爆破，單孔裝藥量為500 g，延時間隔為5 ms。值得一提的是，本文數值模擬為精確多孔齊爆，而目前瞬發工業雷管或同段毫秒雷管難以實現精確的多孔齊爆，即使精度較高的數碼電子雷管也存在±1 ms 的誤差。

地表峰值振速通常隨爆心距呈指數衰減：

式中：v為爆破振動質點最大速度（cm/s)；Q為炸藥量（kg)，齊爆時取總藥量，延時起爆時取單段最大藥量；R為爆源距(m)；d為比例距離；K和 α 分別為爆破點至測點間地形、地質條件的相關系數和衰減指數。

圖9 中給出了兩種爆破模式下地表峰值振速隨比例距離的變化趨勢。由圖9 可知，在總藥量相同的情況下，在相同測點處，延時爆破引起的地表峰值振動速度較齊爆更低，表明延時爆破的降振效果明顯。此外，對比圖9(a)和圖9(b)可以看出，相較于兩種爆破模式下的豎向地表峰值振動速度衰減曲線，水平向地表峰值振動速度衰減曲線的差異較大。這表明，延時爆破顯著降低了爆破施工引起鄰近建筑物水平向的振動響應。

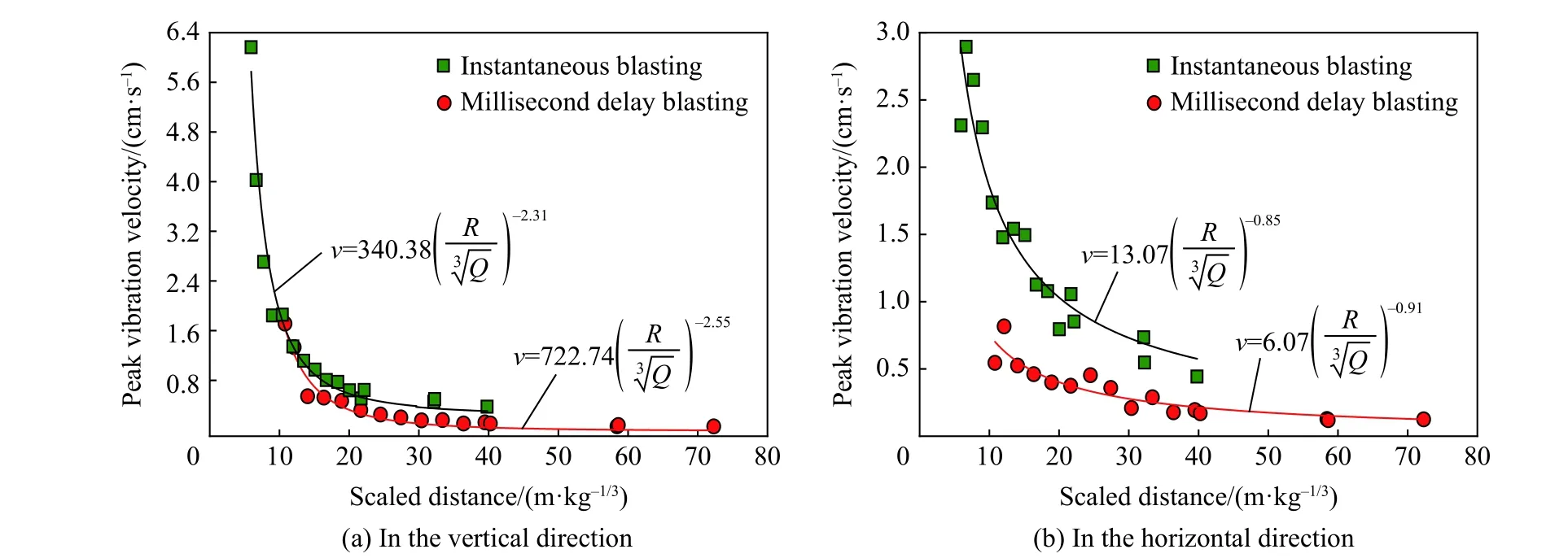
圖9 不同爆破方式下地表振動速度衰減規律對比Fig. 9 Comparison of ground vibration attenuation under different blasting modes

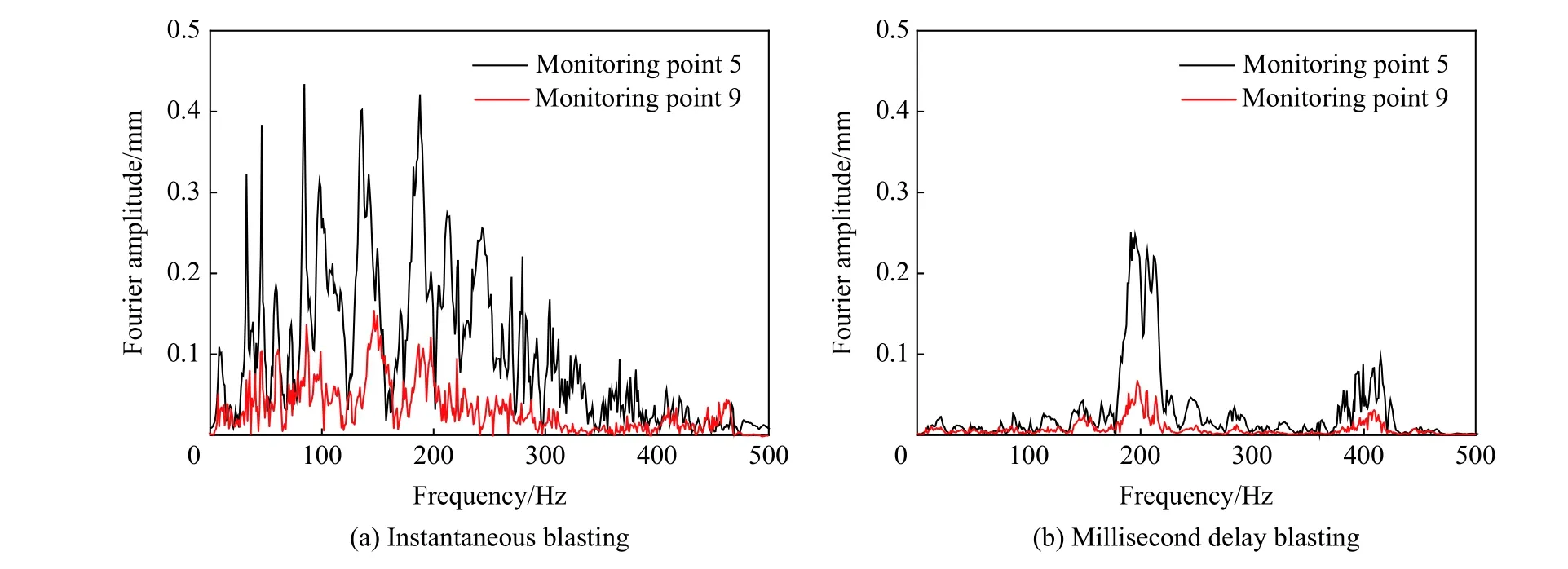
圖10 不同爆破方式下地表測點的頻譜對比Fig. 10 Comparison of frequency spectra at surface monitoring points under different blasting modes

先起爆炮孔的速度波形和后起爆炮孔的波形相互干擾，導致波形峰值相互錯開進而影響頻譜特性[20]。因此，進一步對比兩種工況下地表速度響應(距爆源水平距離8 m)的頻譜特性。圖10 所示：齊爆產生的頻帶分布較廣，并在0～200 Hz 內出現多個峰值；延時爆破產生的頻率成分較單一，主頻也較高，約為200 Hz。從圖10 可以看出，地表土層具有顯著吸收爆破振動中高頻成分的特性，且對總能量有衰減作用。綜上可知，延時爆破對分散爆破振動能量的作用顯著，地表速度響應的主頻較高，更遠離建筑結構自振頻率(見表1)，可顯著降低爆破施工引起的鄰近建筑物的結構振動水平。

6 結 論

依托南京地鐵隧道的爆破振動現場試驗，考慮毫秒延時爆破的不規則荷載作用，采用非線性土體本構模型和改進的Friedlander 方程，建立了地層-爆源體系三維精細化有限元模型，對比分析了50 ms 延時爆破和齊爆引起的環境振動特性，得到的主要結論如下：

（1）采用不規則加卸載準則構造的基于Davidenkov 骨架曲線的應力-應變滯回圈描述場地土動力非線性特性，能夠較好地模擬毫秒延時爆破不規則荷載作用下的土體動力響應。

（2）通過改進的Friedlander 方程來模擬內源爆炸在圓柱形炮孔表面產生的瞬態空氣沖擊波，實現了包含爆破荷載輸入和有限元-無限元耦合邊界的地層-爆破荷載體系的三維精細化有限元模型，與現場實測數據對比驗證了該模型方法的有效性。

（3）兩種爆破方式中，地表峰值振速均隨比例距離的增大而呈指數衰減。50 ms 延時爆破引起的地表振動速度顯著低于齊爆引起的地表振動速度，在地表土層傳播中衰減較快，且地震波主頻集中在高頻段，遠離建筑結構自振頻率，能夠顯著降低鄰近建筑物的結構振動水平。