基于位移影響線的橋梁損傷識別方法

2020-10-21 14:11:37馬浩

大眾科學·中旬 2020年4期

馬浩

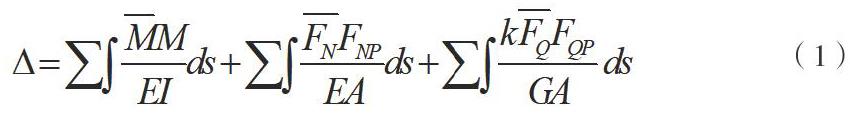
摘要：本文提出了一種基于損傷前后位移影響線差值的包絡線的損傷識別方法。依據荷載作用下結構的位移分析理論，推導了簡支梁損傷前后的位移影響線公式和損傷前后的位移影響線差值公式，結合包絡線的定義，得到了簡支梁橋損傷前后位移影響線差值的包絡線，利用包絡線的一些物理特征對結構進行了損傷識別。為了對該方法進行驗證，以某簡支箱梁橋為研究對象，建立數值分析模型來來進行損傷識別的模擬。結果表明，該方法可以準確的識別出結構損傷位置，對于多處損傷的簡支梁結構也具有良好的識別效果。

關鍵詞：位移影響線差值;包絡線;簡支梁;損傷識別

1引言

結構損傷識別是通過對結構的關鍵性能指標的研究與分析，判斷結構是否存在損傷。現有的損傷檢測技術主要分為動力法和靜力法;基于動力性能指標損傷識別方法由于結構原始數據的獲取受外界環境影響較大，因此得到的結果受到一定限制;而基于靜力性能指標的損傷識別方法能夠得到精度較高的靜力參數，具有良好的識別效果，但每個測點只能代表局部的位移情況，不能反映全橋的位移狀態，如果想獲取全橋的位移狀況則需要多個測點，這在實際工作中是不方便的;利用影響線可以很好的解決這個問題，因此許多學者對影響線理論做了深入的研究。

魏婷婷﹑張延慶等[1]利用位移影響線二階導數對彎橋的損傷進行了識別; 杜永峰.劉云帥[2]利用撓度差值影響線對簡支梁橋進行了損傷位置的判斷，結果表明該方法對單處損傷具有較好的適用性，但對于多處損傷的識別效果不盡人意;張珂苑﹑藺鵬臻[3]通過梁橋的研究，提出了以橋梁損傷前后跨中撓度影響線三次差值為指標的損傷定位方法，結果表明該方法對單處損上和多處損傷的定位具有良好的適用性;吳貴飛﹑張延慶等[4]根據位移影響線理論提出了基于多測點的位移影響線差值曲率的損傷識別方法，結果表明該方法可以識別出簡支梁的損傷位置，但多測點位置的選取對識別的敏感性有影響;陳記豪﹑趙順波[5]提出了利用對稱撓度差值影響線對空心板橋進行損傷識別，結果表明對稱撓度差值影響線的曲率對損傷識別效果較好。

現有的利用位移影響線進行損傷識別研究的方法，都是利用結構上的一個或者幾個測點的位移影響線來判定結構的損傷狀況，這樣識別精度取決于測點位置的選取，尤其是當測點離損傷部位較遠時，識別效果欠佳。為了剔除測點位置選的不同所帶來的影響，本文提出利用位移影響線差值的包絡線對結構進行損傷識別研究。本文將在理論推導的基礎上，以某簡支梁橋為例建立有限元數值模型，通過對數值模型的研究和分析，得到處位移影響線差值包絡線與損傷位置之間的關系，從而為結構的損傷識別提供了新的途徑和方法。

2損傷識別方法的研究

2.1簡支梁位移影響線

撓度影響線的概念是依據內力影響線提出的，即梁上某一點的撓度隨移動荷載位置變化而變化的曲線。由位移互等定理[6]可知，在單位移動荷載下結構跨中位移影響線可以轉化為求解跨中單位力作用下各點的位移。由結構力學可知，結構上任一點在荷載作用下的彈性位移為：

梁結構中，結構的位移主要是由彎矩M引起的變形，而剪力FQ和軸力FN引起的變形影響較小，可忽略不計，因此可得到梁的位移計算公式為：

設有一簡支梁橋（如圖2.1所示），跨長為，截面的抗彎剛度為EI，下面推導跨中D點的撓度影響線。

如圖1所示的結構，在移動荷載P作用下任一截面的彎矩表達式為：

根據變形體的虛功原理知：某一點的豎向線位移，需在該點虛設一單位力P，如圖2所示，在虛擬力P=1的作用下梁上的任一截面的彎矩MP（x）表達式：

當梁發生損傷時其截面的抗彎剛度減小，其余未損傷區域的抗彎剛度不變，假設在損傷區域范圍內梁的抗彎剛度為EI'，其余未損傷梁段的抗彎剛度為EI，利用圖乘法得到簡支梁有損傷時不同區間的撓度影響線為：

將式（3）﹑（4）帶入式（6）～（9）中時，應根據所在的積分區域而選擇相應的和MP（x）表達式。

當結構完好時，梁的抗彎剛度不變，所以只需將式（6）～（9）中的抗彎剛度EI'換成完好時的抗彎剛度EI，即可得到梁在完好時的位移影響線計算公式。

2.2位移影響線差值的包絡線

2.2.1位移影響線差值

由位移影響線計算公式推導可得到損傷前后簡支梁橋D點撓度的差值表達式為：

由以上分析可知，當移動荷載在損傷區域的左側移動時，損傷前后位移影響線的差值與移動荷載的位置呈線性變化，并且是單調遞減的;當移動荷載在損傷區域內移動時，位移影響線的差值與移動荷載的位置呈三次方變化;當移動荷載在損傷區域的右側移動時，移影響線的差值與移動荷載的位置呈線性變化，并且是單調遞增的。

2.2.2位移影響線差值的包絡線

位移影響線差值的包絡線是這樣定義的，給定一個單參數曲線族：

其中為參數，表示一組損傷前后位移影響線的差值，若存在一條曲線，滿足下列條件：

2）對任意的，存在唯一的，使得且與在（x0，y0）有相同的切線。

則稱為曲線族：F（x，y，c）=0的一條包絡線，即曲線為簡支梁損傷前后位移影響線差值的包絡線。這條曲線本身不包含在曲線族中，但過這條曲線上的每一點，在曲線族中都可以找到一條曲線和它在這點相切。

所以，位移影響線差值包絡線的解析式可以表示成：

其中，表示第n點處位移影響線的差值，整個結構總共有n個測點。

將公式（15）和公式（16）中的多個離散點用曲線連接起來就形成了位移影響線差值的包絡線。

3數值算例

3.1模型簡介

計算模型為30m等截面預應力混凝土簡支箱梁橋，其橫斷面為單箱雙室結構，主梁C50混凝土，彈性模量E=3.4×10e4 MPa，泊松比ν=0.2。利用Midas Civil軟件建立簡支梁橋的有限元模型，結構單元劃分密度為1m，全橋總共劃分為30個單元，每個測點布置一個傳感器全橋共31個測點。有限元模型如圖3所示;

3.2數值模擬結果

首先來研究一下結構存在單處損傷時包絡線的變化規律。根據損傷部位和損傷程度的不同，設置損傷工況如表1所示：

利用Midas Civil計算得到簡支梁橋結構發生單一損傷前后撓度差值影響線的包絡線如下圖所示：

觀察圖10可發現：在損傷區段左側，包絡線隨著移動荷載位置的增加而逐漸遞減，并且在損傷區域的一側出現拐點;當移動荷載位于損傷區域內時，包絡線出現新的變化趨勢，并且在損傷區域的另一側，包絡線又出現新的拐點;移動荷載在損傷區域右側時，包絡線呈現線性遞增變化;包絡線的損傷部位在靠近跨中點的一側將會出現極小值點。利用該特點容易判斷出結構的損傷位置。

接下來研究一下結構存在多處損傷時包絡線的變化規律。本階段所建立的損傷工況如表2所示：

通過計算得到簡支梁結構存在多處損傷位置時的包絡線如下圖所示：

由圖11觀察發現：在多損傷工況下，當結構未發生損傷時，包絡線呈現線性變化;在損傷附近，包絡線會出現明顯的拐點，并且在靠近跨中附近的損傷部位處的一側會出現極小值點。說明利用該方法能夠對存在多處損傷部位的結構進行定位識別。

觀察還發現隨著損傷程度的增大，包絡線圍成的面積明顯增大;說明利用位移影響線差值的包絡線也可以對結構的損傷程度進行初步估計。

4結論

本文提出了用位移影響線差值的包絡線方法來識別結構的損傷狀況，利用Midas Civil對一簡支梁橋進行數值模擬，得到如下結論：

1）對于損傷部位靠近端部的情況，利用本文所提到的方法，能夠精確識別出結構發生損傷的位置。

2）對于單位置損傷以及多位置損傷，均能通過位移影響線差值包絡線的斜率變化趨勢，精確定位結構的損傷位置。

3）對于損傷程度的識別，盡管本文所提出的方法可以對結構的損傷程度做出定性判斷，但無法對其進行定量化的估計，所以還需作進一步研究。

參考文獻：

[1]魏婷婷.張延慶.張剛. 彎橋存在損傷時位移影響線的研究[J].科學技術與工程，2014.

[2] 杜永峰.劉云帥.王曉琴.基于撓度差值影響線的簡支梁橋傷識別研究[J]. 甘肅科學學報， 2009.