基于問題鏈的數學微專題設計

【摘?要】在數學微專題中融入問題鏈教學的理念，通過對“認知沖突鏈”“思維導向鏈”“內化提升鏈”“拓展深入鏈”的有序設計，進而推動傳統課堂的轉型，促使學生的學習從“想學”到“學會”“會學”“樂學”的跨越。

【關鍵詞】問題鏈;微專題;兩邊夾

【作者簡介】呂增鋒，中學正高級教師，研究方向為數學教育、微課開發。

【基金項目】浙江省2019年度重點規劃課題“精準·自主·深度：基于‘學歷案的高中數學微專題教學實踐研究”（2019SB051）

數學微專題教學一般運用于高三復習課，雖然與傳統的大專題教學相比，微專題教學具有“因微而準、因微而細、因微而深”的優點，但從本質層面分析，微專題其實就是傳統習題集或復習材料的“濃縮版”或“精華版”。微專題教學還是依賴于“教師講，學生練”的陳舊形式，它無法從根本上促使傳統課堂的轉型與學生學習方式的轉變。

引入“問題鏈”可以有效彌補微專題的不足。一方面，問題鏈為學生提供了數學學習的框架，使學生能夠通過問題鏈獲得較高水平的數學知識;另一方面，問題鏈中問題間的跨度又為學生的高水平思維提供了無限的可能[1]。在數學微專題設計中，如果能夠把問題鏈有機地融入其中，學生就可以通過問題鏈驅動學習的進程，實現數學知識的自主探究與思維的自主建構。下面以“兩邊夾”解題策略微專題為例，淺談基于問題鏈的數學微專題設計。

一、設計“認知沖突鏈”，讓學生想學

數學微專題教學不僅能鞏固和強化學生已有的解題經驗，而且還能讓學生獲得新的解題技巧，優化解題思維。但由于高三學生已經初步具備了一套“行之有效”的解題策略，如何讓已經深受思維定式影響的學生愿意學習并接受新的解題方法是數學微專題設計中首先需要考慮的問題。可以通過制造“認知沖突”來激發學生的學習動機。人都有解決認知沖突的本能，學生一旦發現那些“行之有效”的方法不好用或不能用時，就會促使他們去尋求新的解題方法。

“認知沖突鏈”的設計可以按照“回憶—嘗試—評價—激發”的邏輯主線展開。在學生面對相對陌生的問題時，教師可以先讓學生回憶問題的類別，引導學生從已有的認知結構中尋找解題方法，借助已有的解題經驗去嘗試解題，再對解題過程進行評價，分析原有方法存在的不足，激發學生進一步探索的欲望。

例1?已知函數f（x）=x2-2x-t（t∈R）在區間[0，3]上的最大值為2，則實數t的值為?。

【回憶】教師讓學生思考這道題目屬于哪類問題，以前是否接觸過類似的題目，可以用什么方法來解決。

【嘗試】這是一道求函數最值問題的題目，這個函數是由二次函數外加絕對值構成的，其圖像呈現“W”型，一般可以通過圖像來確定其最值。

學生在解題時需要考慮函數的最大值在什么情況下取得，以及如何確定t的值。

結合圖像，其最大值只有在f（0）=t，f（1）=t+1，f（3）=t-3處取得，然后通過逐一驗證以確定t的值。

①當fmax（x）=f（0）時，即t=±2，

t=2f（1）=3>2，t=-2f（3）=5>2，所以t=±2不符合題意。

②當fmax（x）=f（1）時，即t=1或t=-3，

t=1f（0）=1，f（3）=2，符合題意;t=-3f（0）=3>2，f（3）=6>2不符合題意。

③當fmax（x）=f（3）時，即t=1或t=5，

t=5f（0）=5>2，f（1）=6>2不符合題意。

綜上所述，t=1。

【評價】此題涉及分類討論，解題過程相對煩瑣。解題結束后，教師讓學生思考“能否想到這種解法”“對這種解法有什么看法”。

【激發】教師先肯定學生的解題成果，再針對解題過程存在的弊端，激發學生進一步探究的欲望。

二、設計“思維導向鏈”，讓學生學會

費賴登塔爾認為：“教學過程中所教的東西，要讓學生感覺一切都是當著學生面發生的，而不是以教條形式灌輸的。”波利亞也強調：“要讓學生懂得學習的途徑，學習任何東西的最佳途徑是自己去發現;教師不要立即吐露你的全部秘密，盡量讓學生自己找出來。”因此，數學教學的過程其實就是引導學生自主發現的過程。數學微專題教學不應該只是關注解題技巧、方法的落實，而是應該重在通過設計“思維導向鏈”使學生經歷完整的數學發現的過程，從而實現學生學會學習的目的。

“思維導向鏈”的設計可以按照“提示—回歸—遷移—歸納”的邏輯主線展開。首先，通過提示性的語句打破學生的思維定式，讓學生知道還存在更好的解題方法;然后，讓研究的視角轉向學生熟悉的、相對簡單的題目上，?從而使學生的思維回歸到問題的起點，進而發現新的解題思路;接著，嘗試把解題思路遷移到對復雜問題的解決過程中;最后，經過總結分析，歸納解決問題的核心思想方法。

【提示1】如何把“函數f（x）=x2-2x-t（t∈R）在區間[0，3]上的最大值為2”用不等式表示出來？如何去掉絕對值？

（該問題等價于x2-2x-t≤2。去絕對值一般有兩種方法：一是兩邊平方，但這樣做運算量比較大;二是根據絕對值的定義直接展開，即-2≤x2-2x-t≤2。）

【提示2】能否把參數t表示出來？

（參數分離后，得到x2-2x-2≤t≤x2-2x+2。）

【提示3】不等式x2-2x-2≤t≤x2-2x+2具有什么內在的意義？

（這是一個表示“恒成立”的不等式。）

【回歸】若不等式x2-2x-2≤t在區間[0，3]上恒成立，如何求t的取值范圍？

（問題歸結為求函數g（x）=x2-2x-2在[0，3]上的最大值，利用二次函數的性質，結合圖1，很容易求出gmax（x）=g（3）=1。）

【遷移】如何通過不等式x2-2x-2≤t≤x2-2x+2求t的值？

圖1

（maxx2-2x-2≤t≤minx2-2x+2，借助圖像，如圖1，得到t=1。）

【歸納】解決這個問題的關鍵是什么？需要用到哪些思想方法？

（去絕對值把問題轉換為函數最值問題，通過數形結合思想“夾出”參數的值。）

三、設計“內化提升鏈”，讓學生會學

不經歷深度思考，不經歷“內化”的解題充其量就是低層次的重復訓練，是無法達成“解一題懂一法，會一類通一片”的目標的。內化的過程正是自我反思、自我提高、自我升華的過程。只有經歷這個過程才能真正形成屬于學生自己的數學思想方法體系，才能實現從“學會”到“會學”的跨越。

“內化提升鏈”在微專題中處于核心地位，可以按照“運用—優化—提煉—強化”的邏輯主線展開。首先，讓學生把初步獲得的解題方法大膽地運用到解題中;然后，在實際操作中通過優化解題方法來化解遇到的思維障礙;接著，反思積累解題經驗，使解題方法得到進一步的提煉;最后，在教師的激勵下逐步形成適用性強、靈活多樣的解題策略，強化解題的一般思路。

例2

設a∈R，若x>0時均有[（a-1）x-1]（x2-ax-1）≥0，則實數a的取值為。

【運用】這道題目能否利用上述的解題思路進行解答呢？

圖2

問題等價于[a-（1+1x）][a-（x-1x）]≤0在x>0時恒成立，根據“兩邊夾”思想，實數a的取值“夾在”曲線y=1+1x與y=x-1x之間（如圖2），所以a=32。

例3?已知函數f（x）=2x-ax-b（a，b∈R），對任意的x∈[1，2]，均有f（x）≤m，則實數m的最小值為。

【優化1】此題與例1和例2比較有何不同？

（題目中包含多個參數。）

【優化2】對于包含多個參數的式子如何變形比較合理？

（2x-ax-b≤m-m≤2x-ax-b≤m2x-m≤ax+b≤2x+m①。）

【優化3】如何利用“兩邊夾”思想求①式的m值？

（①式可理解為“兩曲線夾一直線”，如圖3，設M（1，2-m），N（2，1-m），則直線MN的方程為y=-x+3-m，當直線MN與曲線

y=2x+m相切時m的值最小，聯立方程

y=2x+my=-x+3-m

x2+（2m-3）x+2=0，由Δ=0m=3+222。）

圖3

【提煉】經過例3的解答，你有什么收獲？

（不等式變形是解題的關鍵，尤其是對包含多個參數的不等式，雖然其變形有多種形式，但要遵循熟悉以及容易作圖的原則，最后通過圖像“夾”出來。）

【強化】已知f（x）=x2+x-a-3在x∈[-1，1]上的最大值為2，則實數a的值為?。

此題雖然包含了兩個絕對值，但萬變不離其宗，依然可以用“兩邊夾”的思想解決。

四、設計“拓展深入鏈”，讓學生樂學

哲學家卡爾·波普爾認為，愈來愈深化的問題，愈來愈能啟發新問題。通過對微專題中問題鏈的探求，學生學會了一種解題方法，會利用相關的思想方法解決一類數學問題，但這并不是微專題教學的終極目標。隨著問題鏈的不斷拓展和深入，學生在“發現問題—解決問題—再發現問題”的過程中，思維逐漸走向縱深，形成完整的、具有聯系的數學知識體系。

“拓展深入鏈”可以圍繞著“情境拓展”與“方法拓展”兩個層面進行。“情境拓展”旨在通過改變問題的條件、結論與類型，讓學生進一步感受解題方法的普適性;“方法拓展”是對已有的思想方法作適當的改進以適應新的題型，讓學生體會解題方法的靈活性。“拓展深入鏈”能夠為學生帶來成就感，使學生從“會學”走向“樂學”。

例4?已知二次函數滿足f（1）=2，對于x∈R都有-x-1≤f（x）≤2x2+3x+1，求函數f（x）的解析式。

該題看似與前面的含絕對值的最值問題不是同一類題目，但當把x=-1代入不等式-x-1≤f（x）≤2x2+3x+1后，得到0≤f（-1）≤0，這顯然就是“兩邊夾”思想的直接應用。然后利用f（1）=2，f（-1）=0聯立方程即可求出函數f（x）的解析式。

【情境拓展】已知函數f（x）的定義域為R，且對x，y∈R都有f（x+3）≤f（x）+3，f（x+2）≥f（x）+2，若f（1）=2019，則f（2019）=。

兩組不等式f（x+3）≤f（x）+3，f（x+2）≥f（x）+2方向相反，可以利用“兩邊夾”思想建立兩個不等式之間的等量關系。

由f（x+3）≤f（x）+3，f（x+2）≥f（x）+2得，f（x）≥f（x+3）-3f（x+1）≥f（x+4）-3≥f（x+2）-1≥f（x）+1;

f（x）≤f（x+2）-2f（x+1）≤f（x+3）-2≤f（x）+1，所以f（x+1）=f（x）+1，f（2019）=f（2018）+1=f（2017）+2=…=f（1）+2018=4037。

【方法拓展】設函數f（x）=x-ax-b，a，b∈R，若對任意實數a，b，總存在實數x0∈[0，4]使不等式f（x0）≥m成立，求實數m的取值范圍。

該題雖然與前面的例題存在相似之處，但無法直接用前面“兩邊夾”的解題步驟，需要對“兩邊夾”思想進行改進。

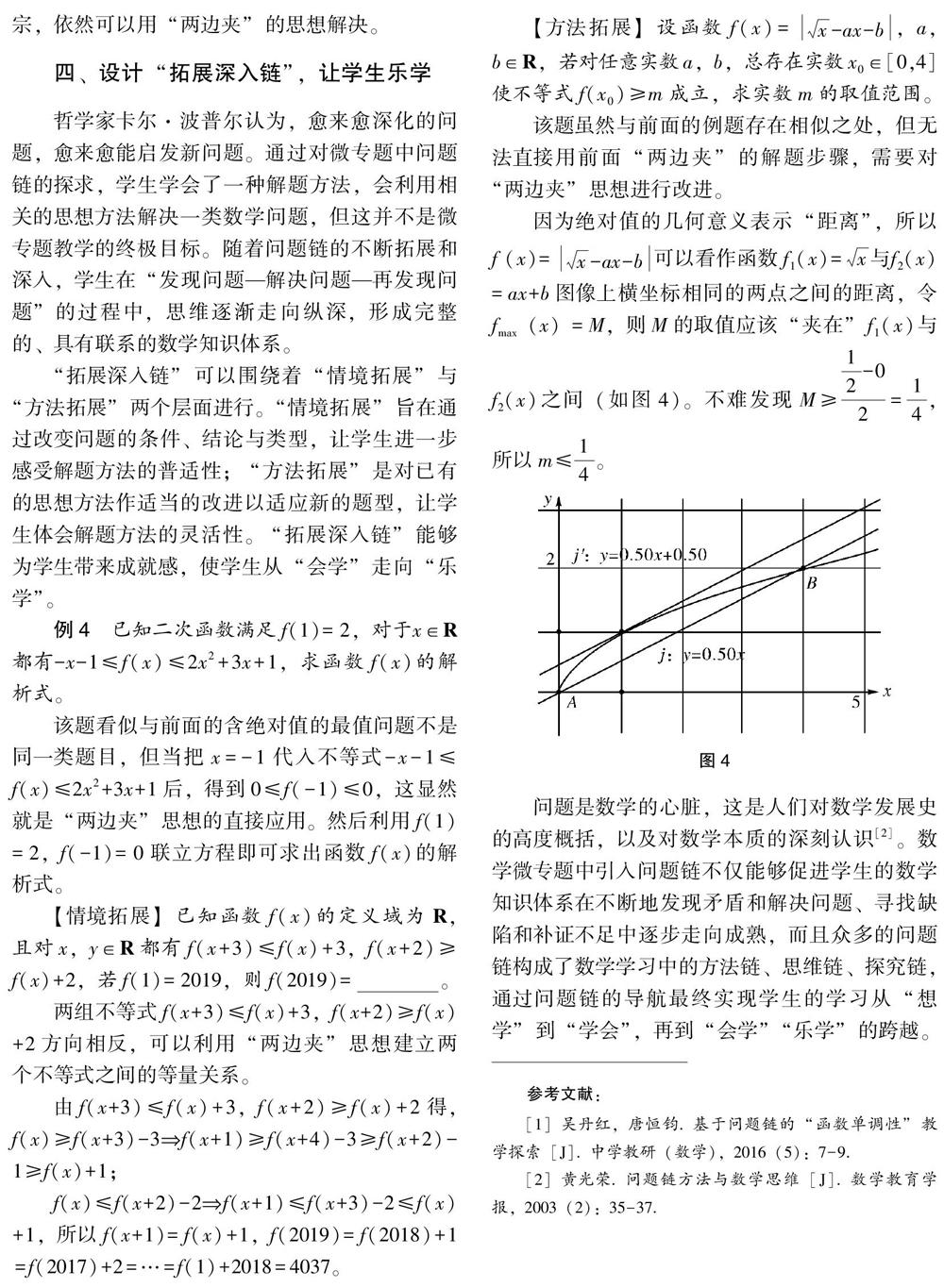
因為絕對值的幾何意義表示“距離”，所以f?（x）=x-ax-b可以看作函數f1（x）=x與f2（x）=ax+b圖像上橫坐標相同的兩點之間的距離，令fmax（x）=M，則M的取值應該“夾在”f1（x）與f2（x）之間（如圖4）。不難發現M≥12-02=14，所以m≤14。

圖4

問題是數學的心臟，這是人們對數學發展史的高度概括，以及對數學本質的深刻認識[2]。數學微專題中引入問題鏈不僅能夠促進學生的數學知識體系在不斷地發現矛盾和解決問題、尋找缺陷和補證不足中逐步走向成熟，而且眾多的問題鏈構成了數學學習中的方法鏈、思維鏈、探究鏈，通過問題鏈的導航最終實現學生的學習從“想學”到“學會”，再到“會學”“樂學”的跨越。

參考文獻：

[1]吳丹紅，唐恒鈞.基于問題鏈的“函數單調性”教學探索[J].中學教研（數學），2016（5）：7-9.

[2]黃光榮.問題鏈方法與數學思維[J].數學教育學報，2003（2）：35-37.