探究“一線三等角”模型解題攻略

曾 靜

【摘要】 利用MM策略數(shù)學(xué)建模思想是重要的教與學(xué)的思想，靈活掌握和應(yīng)用數(shù)學(xué)模型解題是解決綜合題型的重要突破方法。巧用”一線三等角”模型能更好地突破數(shù)學(xué)綜合題，拓寬學(xué)生的解題思路，拓展學(xué)生的解題思維，讓學(xué)生獲取學(xué)習(xí)數(shù)學(xué)的靈性，讓學(xué)習(xí)數(shù)學(xué)變得更有趣。現(xiàn)代數(shù)學(xué)理念認(rèn)為數(shù)學(xué)教學(xué)是數(shù)學(xué)思維過程的教學(xué)。數(shù)學(xué)教學(xué)不僅要使學(xué)生獲得新的知識，而且要提高學(xué)生的思維能力，要培養(yǎng)學(xué)生自覺運用數(shù)學(xué)知識考慮和處理實際問題，從而形成良好的思維品質(zhì)。

【關(guān)鍵詞】 數(shù)學(xué)建模思想 一線三等角模型 數(shù)學(xué)綜合題

【中圖分類號】 G633.6

【文獻(xiàn)標(biāo)識碼】 A

【文章編號】 1992-7711（2020）02-171-020

數(shù)學(xué)課標(biāo)實驗本在前言部分11次提到了數(shù)學(xué)的建模，用模問題，數(shù)學(xué)建模的思想對提高初中生數(shù)學(xué)思維能力有很大的促進(jìn)的作用，它能使學(xué)生真正把數(shù)學(xué)學(xué)會學(xué)活，達(dá)到深化、理解知識、發(fā)展應(yīng)用數(shù)學(xué)的思維能力，促進(jìn)數(shù)學(xué)素質(zhì)的提高。

利用數(shù)學(xué)模型思想，讓教師們在教學(xué)中不是按點教學(xué)，不只為講一個知識點或講一道題，而是按塊教學(xué)，運用綜合知識解決一類有共性的題，歸納出模型。利用數(shù)學(xué)模型思想教學(xué)滲透到平時的實際教學(xué)中，能提高學(xué)生們的數(shù)學(xué)思維能力，讓學(xué)生在面對綜合題時不會束手無措，模型思想的可以給學(xué)生提供更合適的解題思路，減低學(xué)生的思維量，提高解題信心，緩解學(xué)生解題的緊張感。

學(xué)生到了九年級，數(shù)學(xué)知識累積到了一定程度，但很多知識較模糊，尤其是對于解決綜合題更是無從下手，數(shù)學(xué)模型思想的學(xué)習(xí)，模型的應(yīng)用在一定程度上能開拓學(xué)生的解題思路，在獨立解題上能更好地引導(dǎo)自己解題突破，學(xué)生一旦發(fā)現(xiàn)題目有熟悉感，離解題成功也就不遠(yuǎn)了。

在眾多的數(shù)學(xué)幾何模型中，一線三等角模型應(yīng)用頻率很高，在綜合題中起到關(guān)鍵的解題突破的作用。什么是一線三等角模型，它突出的特點就是構(gòu)造兩組角對應(yīng)相等。具體的定義描述是：

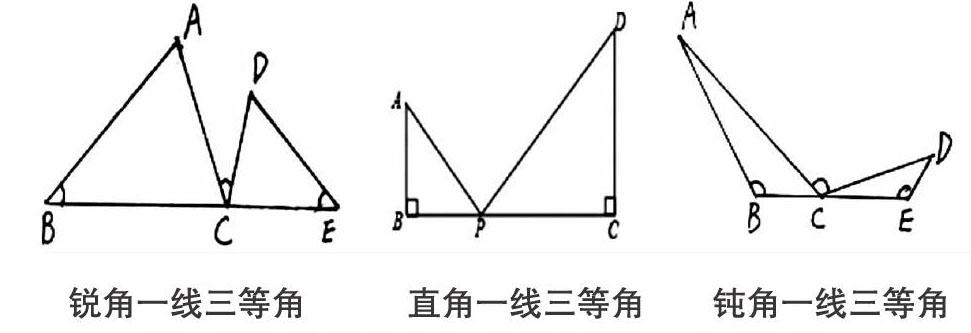
兩個相等的角一邊在同一條直線上，另一邊在該直線的同側(cè)或異側(cè)，第三個與之相等的角的頂點在前一組等角的頂點中所確定的線段上或線段的延長線上，另外兩邊分別位于一直線的同側(cè)或異側(cè)與兩等角兩邊相交，會形成一組相似三角形，習(xí)慣上把該組相似三角形稱為“一線三等角型”相似三角形。（通俗地講，一條直線上有三個相等的角一般都會存在相似三角形。）較常見的“一線三等角型”按角分，分別有“銳角一線三等角”、“直角一線三等角”、“鈍角一線三等角”，三種模型如下圖

銳角一線三等角 直角一線三等角鈍角一線三等角

一線三等角模型適用于三角形全等和三角形相似。

直角一線三等角模型尤為常用，在代數(shù)的函數(shù)和幾何中，都能靈活應(yīng)用，這模型的熟練掌握通常能順利幫助學(xué)生攻破難題，解題得心應(yīng)手。

例1是直角一線三等角模型應(yīng)用于幾何綜合題型。此題在圖1直角一線三等角模型基礎(chǔ)上做小變題，增加一些條件，便可以成為豐富的出題素材。

圖1 圖2 圖3

例1：如圖2，P在線段BC上，BP=CP，∠B=∠APD=∠C=90°，證明：△ABP∽△APD。本題的題干是很好的出題載體，可以產(chǎn)生不少結(jié)論。

常見的結(jié)論有：

上述這六個結(jié)論中，第一個結(jié)論要用二次相似，對于考生來說較難，突破了結(jié)論①，后面的五個結(jié)論都可以由它演變而來。結(jié)論①的思路如下：

由直角三角形一線三等角模型，易證△ABP∽△PCD，可得■=■，由條件PC=BP等量代換，得到■=■，再結(jié)合∠B=∠APD=90°，可證△ABP∽△APD，從而得到結(jié)論①。

勾股定理的證明方法有600余種，其中美國第二十任總統(tǒng)加菲爾德的證法在數(shù)學(xué)史上被傳為佳話，被稱為“總統(tǒng)證法”，圖形的構(gòu)造就是利用了直角一線三等角模型，如圖3.這種勾股定理的證明方法簡單、直觀、簡捷、易懂和明了。

接下來再看看直角一線三等角在函數(shù)題中的出色表現(xiàn)。

例2：如下圖，∠AOB=90°，且OA、OB分別與函數(shù)y=-■（x<0）、y=■（x>0）的圖象交于A、B兩點，則tan∠OBA的值是? ? ? ? .

分析：過點A作AC⊥x軸于點C，過點B作BD⊥x軸于點D構(gòu)造一線三等角模型。得△OBD∽△AOC，■=（■）2，又點A在反比例函數(shù)y=■（x<0）的圖象上，S△AOC=1，S△OBD=■，可得tam∠OBA=■=■.

這道題是函數(shù)綜合題，題面上學(xué)生要利用反比例函數(shù)的圖象性質(zhì)和正切的定義解題，但這樣不能進(jìn)行難點突破。本題需要充分挖掘題干和圖形的隱含條件，利用反比例函數(shù)的幾何意義并結(jié)合一線三等角模型得到三角形相似，應(yīng)用三角形相似的性質(zhì)和正切的定義便能順利解題。本題解題思路的巧妙，一線三等角功不可沒，若能理解和感受到解題的過程，學(xué)生會被這題的魅力折服，讓獨立答題的學(xué)生們享受解答數(shù)學(xué)的成功感，讓學(xué)生明確到數(shù)學(xué)模型的重要性，在以后學(xué)習(xí)數(shù)學(xué)的過程中，會主動嘗試?yán)媚Ｐ退枷肴フ莆諗?shù)學(xué)知識，從而讓學(xué)生的數(shù)學(xué)思維能力得以提高。

一線三等角模型擅長隱藏，它在上題中隱藏在反比例函數(shù)圖象里不易發(fā)覺，有時它也會藏在等腰三角形、等邊三角形甚至是平面直角坐標(biāo)系里。

例3：如圖，在等邊三角形ABC中，點D，E分別在BC，AB上，且∠ADE=60°.求證：△ADC∽△DEB.

分析：挖掘等邊三角形的隱含條件，可得∠ADE=∠B=∠C=60°，由一線三等角模型，易證△ADC∽△DEB.本題把等邊三角形改成等腰三角形，利用等邊對等角，再增加一角相等同樣構(gòu)造一線三等角模型。

一線三等角模型常應(yīng)用在綜合的數(shù)學(xué)題里，它不但便于解決相似問題，而且同樣可以解決全等問題。一線三等角模型能提供三個相等的角，可以提煉出兩組角對應(yīng)相等的條件，若能結(jié)合題意能找到任意一組邊對應(yīng)相等，三角形全等便成立了。總而言之，有邊相等證全等，沒邊相等證相似。

數(shù)學(xué)教學(xué)的根本任務(wù)，在于教會學(xué)生如何學(xué)習(xí)、如何思考問題、如何應(yīng)用知識解決實際問題，數(shù)學(xué)教師應(yīng)該教育自己的學(xué)生學(xué)會把實際問題轉(zhuǎn)化為數(shù)學(xué)問題加以解決，即建立數(shù)學(xué)模型。也許很多教師都會問：“為什么自己的學(xué)生這么笨，分析和解決實際問題的能力這么差”，其實這跟我們平時的教學(xué)有很大的關(guān)系，正因為我們沒有對學(xué)生進(jìn)行建立數(shù)學(xué)模型的系統(tǒng)訓(xùn)練，沒有培養(yǎng)學(xué)生的建模意識。

培養(yǎng)初中生“數(shù)學(xué)建模”的核心素養(yǎng)的研究，旨在從學(xué)生學(xué)習(xí)和發(fā)展的角度出發(fā)，以數(shù)學(xué)建模為突破點，從而提升學(xué)生的數(shù)學(xué)核心素養(yǎng)。數(shù)學(xué)建模既是學(xué)生學(xué)習(xí)的數(shù)學(xué)思想方法，也是學(xué)生學(xué)習(xí)數(shù)學(xué)知識、解決問題的一種能力。學(xué)生親自經(jīng)歷模型建立的“再創(chuàng)造”過程，有助于培養(yǎng)學(xué)生初步學(xué)會運用數(shù)學(xué)的思維方式去觀家和分析現(xiàn)實社會，解答日常生活中的問題，進(jìn)而形成通于探索、勇于創(chuàng)新的科學(xué)精神，靈活地運用代數(shù)方法解決幾何問題是值得研究和探索的。在中考科目中，數(shù)學(xué)最能體現(xiàn)差距，作為數(shù)學(xué)的教育工作者，幫助學(xué)生提高數(shù)學(xué)思維能力是我們的必修課，有利于提高學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣，有利于提高學(xué)生的數(shù)學(xué)成績，同時又可以減輕學(xué)生學(xué)習(xí)的負(fù)擔(dān)，最大限度地開發(fā)學(xué)生的潛能。

掌握正確的技巧和重視方法總結(jié)，往往事半功倍。數(shù)學(xué)看似變化莫測，實則很多題都可以抽象出基本模型。抓住模型，抓住本質(zhì)，方能以不變應(yīng)萬變。當(dāng)然，一切方法都建立在一定的知識基礎(chǔ)上，打好基礎(chǔ)才能更有效地學(xué)習(xí)。

[ 參? 考? 文? 獻(xiàn) ]

[1]裴娣娜.教育研究方法導(dǎo)論.安徽教育出版社（現(xiàn)代教育原理從書）.1995.8.

[2]袁振國.教育研究方法.高等教育出版社（面向21世紀(jì)課程教材）.2000.7（2018.8重印）.

[3]張志存.例談方程思想在解題中是應(yīng)用.中國教育與教學(xué).2006年10月.第4卷第8期.

[4]全國數(shù)學(xué)建模工作委員會編.初中生數(shù)學(xué)建模能力培養(yǎng)教程.濟(jì)南出版社.2014.9.

[5]猿輔導(dǎo)編著.《中考必會幾何模型》.地質(zhì)出版社.2017.12.