不同儲(chǔ)藏條件下筒倉(cāng)中大豆堆高安全域研究

王 穎 程緒鐸 馮家暢 陳 雪

(南京財(cái)經(jīng)大學(xué)食品科學(xué)與工程學(xué)院，江蘇省現(xiàn)代糧食流通與安全協(xié)同創(chuàng)新中心, 南京 210046)

大豆是生物體，儲(chǔ)藏在筒倉(cāng)深處的大豆籽粒受到很大的壓力，當(dāng)壓力超過籽粒承受范圍時(shí)，籽粒會(huì)產(chǎn)生大的塑性變形甚至發(fā)生破裂，大豆含水率越大，結(jié)構(gòu)越松軟，抵抗壓力的能力越小。變形或破裂的大豆更易于微生物的滋生，影響大豆的安全儲(chǔ)藏和食用品質(zhì)。筒倉(cāng)中的大豆籽粒受力隨著深度的增加而增大，底層的大豆籽粒受力最大，筒倉(cāng)中大豆堆高越高，底層大豆籽粒受力越大，受到損傷越大。因此，為了筒倉(cāng)中儲(chǔ)藏的大豆籽粒結(jié)構(gòu)不受大的損傷與破裂，給出堆高安全域具有重要的現(xiàn)實(shí)意義與應(yīng)用價(jià)值。

裴建國(guó)等[1]研究了增加甜菜堆高度對(duì)甜菜保藏的影響，結(jié)果表明外界溫度與甜菜品質(zhì)均是影響堆高的因素。謝奇珍等[2]的研究提出了不同含水率的散裝存放和袋裝存放油菜籽的堆高原則。沈玉君等[3]建立了氧氣一維擴(kuò)散的模型方程，并計(jì)算出堆肥的堆體優(yōu)化高度。

本研究建立筒倉(cāng)中大豆分層壓縮平衡微分方程，實(shí)驗(yàn)測(cè)定微分方程中的參數(shù)，數(shù)值求解壓縮平衡微分方程得到筒倉(cāng)內(nèi)大豆堆應(yīng)力分布值；建立筒倉(cāng)中大豆籽粒堆放模型，求解大豆籽粒堆放模型得出筒倉(cāng)內(nèi)大豆堆應(yīng)力與籽粒壓力的關(guān)系；實(shí)驗(yàn)測(cè)定大豆籽粒壓力與塑性應(yīng)變關(guān)系；設(shè)定大豆籽粒損傷的塑性應(yīng)變?yōu)?.4%，結(jié)合筒倉(cāng)內(nèi)不同深度大豆堆應(yīng)力、籽粒壓力與塑性應(yīng)變，得出不同儲(chǔ)藏條件筒倉(cāng)中大豆的堆高安全域。

1 材料與儀器

1.1 實(shí)驗(yàn)材料

大豆(綏農(nóng)26)，產(chǎn)自黑龍江，原始含水率為13.43%。實(shí)驗(yàn)時(shí)，將大豆含水率調(diào)為8.58%、10.75%、13.43%、 15.01%。

1.2 實(shí)驗(yàn)儀器與設(shè)備

LHT-1型糧食回彈模量測(cè)定儀，Brookfield質(zhì)構(gòu)儀：CT3(50 kg)。

2 實(shí)驗(yàn)與計(jì)算原理

2.1 筒倉(cāng)中大豆堆應(yīng)力分布模型[4]

2.1.1 大豆堆密度與豎直壓應(yīng)力(最大主應(yīng)力)的關(guān)系

筒倉(cāng)中大豆堆密度取決于大豆的應(yīng)力狀態(tài)(最大主應(yīng)力與最小主應(yīng)力)。將大豆放入LHT-1糧食回彈模量?jī)x的裝樣筒中，施加頂部壓力，大豆處于主動(dòng)應(yīng)力狀態(tài)，主動(dòng)力是大豆重力與頂部壓力，被動(dòng)力是圓筒壁的反力。裝樣筒為剛性不銹鋼筒柱，大豆受壓只在豎直方向產(chǎn)生形變，此時(shí)鋼筒柱中大豆的應(yīng)力與應(yīng)變狀態(tài)和筒倉(cāng)中的大豆的應(yīng)力與應(yīng)變狀態(tài)相似，因此，頂部施加不同的壓力可模擬筒倉(cāng)中不同深度大豆的應(yīng)變與應(yīng)力狀態(tài)。

設(shè)回彈模量?jī)x的裝樣筒內(nèi)徑為Rc，裝入大豆的高度為H，使用微元法，選擇距離大豆堆表面深度為y，高度為dy的微元體進(jìn)行受力分析，微元體在豎直方向的受力見圖1。

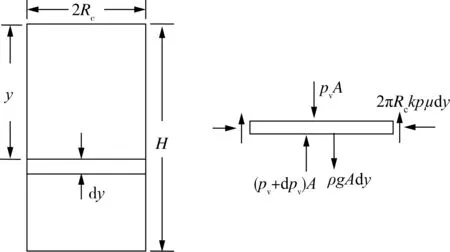
圖1 裝樣筒中大豆微元體的受力圖

根據(jù)Rankine理論[5]，大豆堆側(cè)向壓應(yīng)力與豎直壓應(yīng)力的比為：

(1)

式中：φ為大豆堆內(nèi)摩擦角/°；ph為大豆堆的側(cè)向壓應(yīng)力/kPa；pv為大豆堆的豎直壓應(yīng)力/kPa。

大豆微元體在豎直方向上受力平衡：

(2)

式中：ρ為大豆堆密度/kg/m3；μc為大豆堆與不銹鋼板的摩擦系數(shù)；Ac為裝樣筒的橫截面積/m2。

(3)

(4)

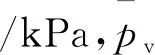
測(cè)得大豆樣品的壓縮體積V，質(zhì)量m，密度ρ=m/V，結(jié)合式(3)、式(4)得到大豆堆壓縮密度與最大主應(yīng)力的關(guān)系方程為：

ρ=F(pv)

(5)

2.1.2 筒倉(cāng)中大豆壓縮與平衡微分方程[6]

假設(shè)筒倉(cāng)的直徑為D，筒高為H，大豆堆內(nèi)摩擦角為φ，倉(cāng)壁與大豆之間的摩擦系數(shù)為μ，假定豎直壓應(yīng)力與水平壓應(yīng)力的大小不隨筒倉(cāng)內(nèi)徑向的大小和方向而變化。選擇距離大豆堆表面深度為y，高度為dy的微元體進(jìn)行受力分析，如圖2所示。

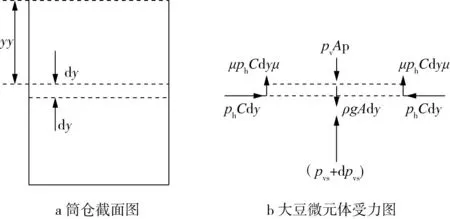
圖2 筒倉(cāng)中微元體受力圖

根據(jù)圖2b可知，微元層在豎直方向上合力為零，則：

(pv+dpv)A+μphCdy-pvA-ρgAdy=0

(6)

式中：A為筒體的橫截面面積/m3；C為筒體的周長(zhǎng)/m。

在Janssen方程中，筒倉(cāng)內(nèi)大豆的最小主應(yīng)力(ph)和最大主應(yīng)力(pv)之比k為：

(7)

結(jié)合式(5)～式(7)得到筒體中大豆分層平衡微分方程組：

(8)

式中：R=D/4，為水力半徑/m。

2.2 筒倉(cāng)深處大豆應(yīng)力與籽粒接觸力的關(guān)系模型[7]

2.2.1 筒倉(cāng)中大豆籽粒的堆放結(jié)構(gòu)

假設(shè)大豆籽粒是等尺寸的小球，在筒倉(cāng)中準(zhǔn)六邊形堆放，如圖3所示，在這種堆放中，水平方向大豆籽粒之間分開一個(gè)小的距離。大豆籽粒分開的距離取決于大豆堆的密度，用結(jié)構(gòu)角θ來表示這個(gè)分開的距離，對(duì)于六邊形堆放(水平方向大豆籽粒之間零距離)，結(jié)構(gòu)角是60°。在筒倉(cāng)深處大豆堆放是準(zhǔn)六邊形堆放，結(jié)構(gòu)角θ取55 °。

筒倉(cāng)中大豆堆由一系列的厚度為ΔH的大豆籽粒層構(gòu)成(見圖4)，大豆層的厚度ΔH為：

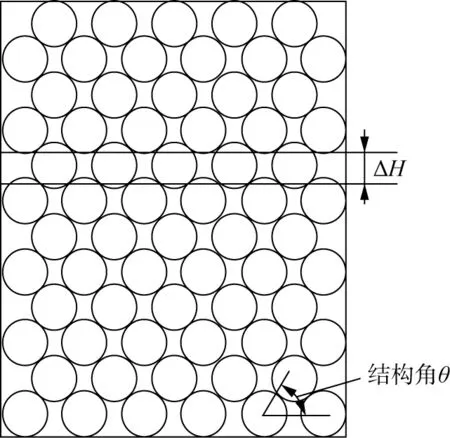
圖3 筒倉(cāng)中大豆籽粒的準(zhǔn)六邊形堆放結(jié)構(gòu)

ΔH=dsinθ

(9)

筒倉(cāng)中大豆的總層數(shù)為：

(10)

式中：H為大豆堆的深度/m。

第i層大豆的深度為：

hi=idsinθ(i=1，2，…，n)

(11)

2.2.2 筒倉(cāng)中大豆籽粒間的接觸力

在中間的第i層大豆籽粒，每個(gè)大豆籽粒與其他4個(gè)大豆籽粒接觸(見圖4a)，此大豆籽粒的力的平衡方程在豎直方向的分量為：

(12)

式中：m為大豆籽粒的質(zhì)量/kg；g為重力加速度/m/s2；F為大豆籽粒間摩擦力/N；N為大豆籽粒間正壓力/N。

圖4 大豆籽粒的力的平衡

筒倉(cāng)是軸對(duì)稱的，若倉(cāng)墻的摩擦不計(jì)，那么2個(gè)摩擦力是相等的，2個(gè)正壓力也是相等的，即：

(13)

將方程(13)代入方程(12)得：

(14)

大豆堆最上層大豆籽粒中，每個(gè)大豆籽粒僅與兩個(gè)大豆籽粒接觸(見圖4b)， 大豆籽粒的力的平衡方程在豎直方向的分量為：

(15)

將方程(13)代入方程(15)得

(16)

2.2.3 筒倉(cāng)深處大豆應(yīng)力與籽粒接觸力的關(guān)系

為了確定大豆平均應(yīng)力與籽粒接觸力的關(guān)系，選取5個(gè)大豆籽粒構(gòu)成的體積元(見圖4a)，該體積元在豎直方向和水平方向的面積分別為：

Sl=2d2sinθ

(17)

Sv=2d2cosθ

(18)

大豆籽粒的平均水平應(yīng)力和豎直應(yīng)力為：

(19)

(20)

式中：phi為第i層平均水平應(yīng)力；pvi為第i層平均豎直應(yīng)力，i= 2，…，n-1。

相鄰層籽粒壓力與摩擦力相差很小，即，Ni-1Ni，F(xiàn)i-1Fi。結(jié)合該條件和方程(7)、(14)、(19)、(20)得到：

(21)

首先求解方程(16)和方程(21)得到N1和F1，接著求解方程(14)和方程(21)得到Ni和Fi(i= 2，…，n-1)，最后求解方程(20)得到平均豎直應(yīng)力與大豆籽粒接觸力的關(guān)系。

2.3 大豆籽粒受損時(shí)塑性應(yīng)變值的確定[8,9]

大豆籽粒受壓時(shí)產(chǎn)生應(yīng)變，壓力較小時(shí)主要產(chǎn)生彈性應(yīng)變，當(dāng)壓力除去后，彈性應(yīng)變消失，籽粒未受到損傷；壓力較大時(shí)產(chǎn)生彈性應(yīng)變和塑性應(yīng)變，當(dāng)壓力除去后，彈性應(yīng)變消失，但塑性應(yīng)變不消失，籽粒受到損傷。本研究使用質(zhì)構(gòu)儀對(duì)90粒大豆籽粒進(jìn)行先加載后卸載，大豆籽粒平均直徑是6.52 mm，加載使大豆變形達(dá)到0.15 mm(總應(yīng)變是0.023)后卸載；卸載后，大豆籽粒塑性變形(殘留變形)量為0.026 mm，塑性應(yīng)變?yōu)?.004，可認(rèn)為大豆籽粒內(nèi)部結(jié)構(gòu)受到了損傷。本研究設(shè)定大豆籽粒受損時(shí)塑性應(yīng)變值為0.4%。

本研究測(cè)定了大豆籽粒的破壞力、破壞應(yīng)變、破壞應(yīng)力，見表1。籽粒破壞時(shí)的應(yīng)變(0.182～0.346)遠(yuǎn)大于籽粒損傷應(yīng)變0.023(塑性應(yīng)變?yōu)?.004)。

表1 不同含水率大豆籽粒破壞力、破壞應(yīng)變、破壞應(yīng)力

3 結(jié)果與分析

3.1 大豆籽粒發(fā)生0.004 塑性應(yīng)變時(shí)的壓力

使用質(zhì)構(gòu)儀測(cè)定不同含水率(8.58%、10.75%、13.43%、15.01% w.b.)大豆籽粒產(chǎn)生塑性應(yīng)變0.004時(shí)受到的壓力，見表2。

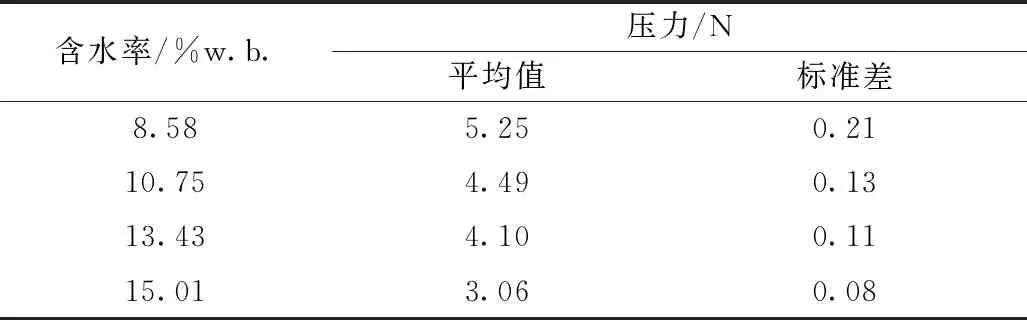
表2 不同含水率大豆籽粒發(fā)生0.004 塑性應(yīng)變時(shí)的壓力

3.2 筒倉(cāng)中大豆籽粒在不同深度受到的壓力

選取筒倉(cāng)的參數(shù)見表3。取θ=55°，φ=30°，求解方程(8)計(jì)算出不同深度大豆堆的豎直壓應(yīng)力，結(jié)合式(14)、式(16)、式(20)、式(21)，可以計(jì)算出筒倉(cāng)內(nèi)不同含水率大豆籽粒在不同深度受到的壓力，見表4～表7。

表3 筒倉(cāng)的參數(shù)

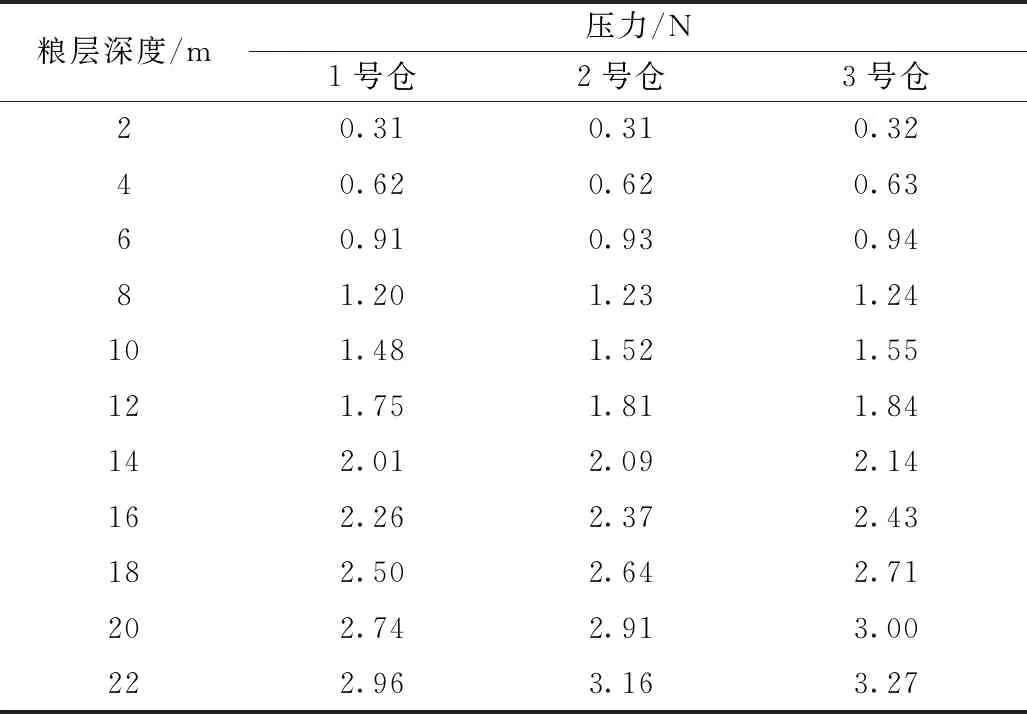
表4 不同糧層深度含水率為8.58% w.b.的大豆籽粒受到的壓力

續(xù)表4

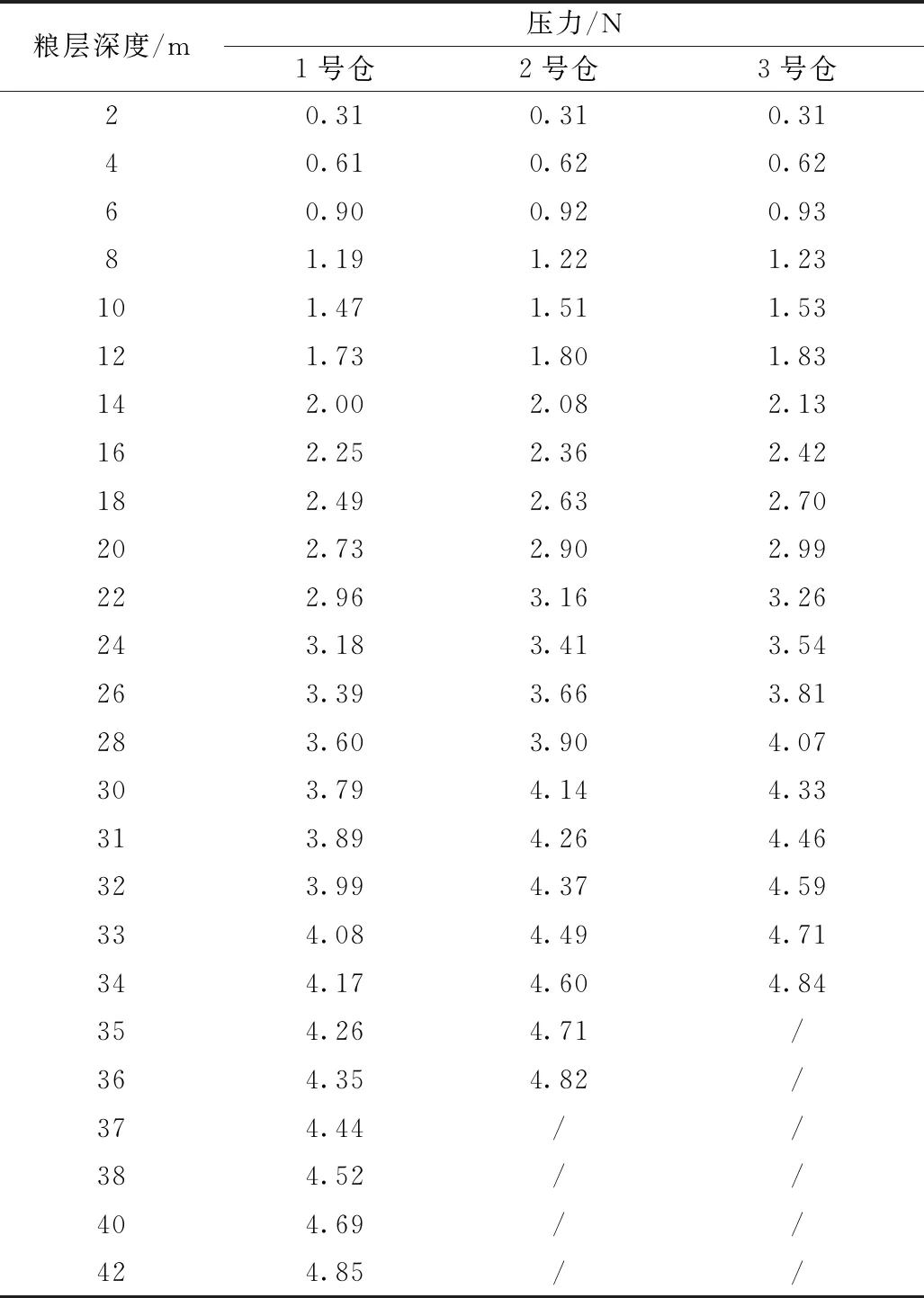
表5 不同糧層深度含水率為10.75% w.b.的大豆籽粒受到的壓力

表6 不同糧層深度含水率為13.43% w.b.的大豆籽粒受到的壓力

3.3 不同含水率大豆的堆高安全域

對(duì)照表2和表4～表7的數(shù)據(jù)，得出不同倉(cāng)型中各含水率大豆堆安全堆高，見表8。筒倉(cāng)內(nèi)大豆堆的安全堆高隨著含水率的增大而減小，隨著筒倉(cāng)直徑的增大而減小。

3.4 不同儲(chǔ)藏期大豆堆堆高的安全域

使用質(zhì)構(gòu)儀測(cè)定不同儲(chǔ)藏期大豆籽粒發(fā)生0.004塑性應(yīng)變時(shí)受到的壓力，結(jié)果見表9。

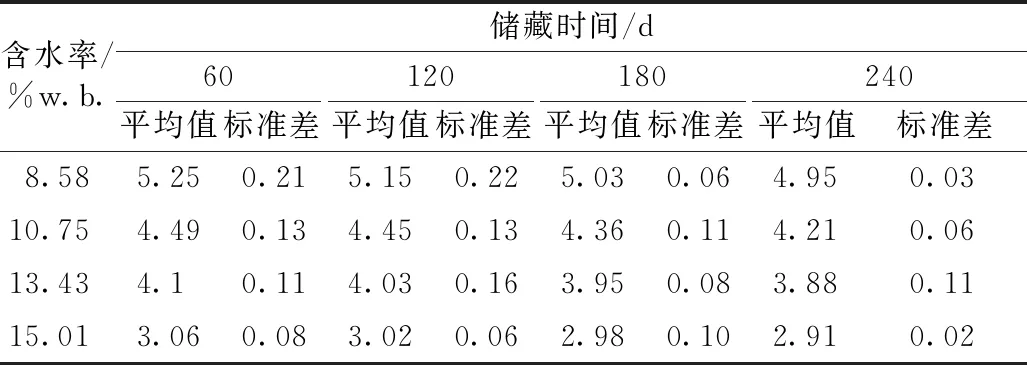
表9 不同儲(chǔ)藏期大豆籽粒產(chǎn)生0.004塑性應(yīng)變時(shí)的壓力

結(jié)合表4～表7的數(shù)據(jù)，由表9可推出不同儲(chǔ)藏期大豆堆高的安全高度，見表10。同一含水率的大豆安全堆高隨著儲(chǔ)藏期的增大而減小，同一儲(chǔ)藏期的大豆安全堆高隨著含水率的增大而減小。含水率為8.58%～15.01% w.b.的大豆在半徑為10 m的筒倉(cāng)內(nèi)儲(chǔ)藏60～240 d，安全堆高的范圍是20.6～47.6 m；在半徑為15 m的筒倉(cāng)內(nèi)儲(chǔ)藏60～240 d，安全堆高的范圍是19.3～40.2 m；在半徑為20 m的筒倉(cāng)內(nèi)儲(chǔ)藏60～240 d，安全堆高的范圍是18.8～37.4 m。

4 結(jié)論

本研究建立筒倉(cāng)中大豆分層壓縮平衡微分方程及大豆籽粒堆放模型，求解微分方程及堆放模型得出筒倉(cāng)內(nèi)大豆堆應(yīng)力與籽粒壓力的分布值，結(jié)合實(shí)驗(yàn)測(cè)定的大豆籽粒壓縮力與塑性應(yīng)變關(guān)系，得出大豆的堆高安全域。結(jié)果表明，含水率為8.58%～15.01% w.b.且儲(chǔ)藏時(shí)間為60～240 d的大豆，在半徑為10 m的筒倉(cāng)內(nèi)安全堆高的范圍是20.6～47.6 m；在半徑為15 m的筒倉(cāng)內(nèi)安全堆高的范圍是19.3～40.2 m；在半徑為20 m的筒倉(cāng)內(nèi)安全堆高的范圍是18.8～37.4 m。筒倉(cāng)內(nèi)大豆堆的安全堆高均隨著含水率、筒倉(cāng)直徑、儲(chǔ)藏期的增大而減小。

表10 不同含水率大豆不同儲(chǔ)藏期堆高安全域/m