基于數學方法論的“深度”解題

劉鵬　盧象鵬　楊光偉

[摘? 要] 思維能力的培養是學生發展數學核心素養的關鍵之一. 數學方法論指導下的“深度”解題為學生開展數學探究活動提供了思路. 以一節不等式證明的解題教學為例討論在實施這種教學時需要關注的問題.

[關鍵詞] 思維能力;“深度”解題;數學方法論

思維能力的培養是學生發展數學核心素養的關鍵之一. 鄭毓信先生曾提到：在教學中不僅要關注學生“即興思維”能力的提高，還應當更加重視如何能夠幫助他們逐步養成“長時間思考”的習慣和能力[1]. 學生數學思考的脈絡化是培養其思維能力的重要途徑，而在數學方法論指導下的解題探究教學則能為有脈絡地探索活動提供一定的借鑒意義.本文將從一個數學解題探究的教學案例出發，探析學生是如何在基于數學方法論的“深度”解題過程中，有脈絡地思考.

數學方法論背景下“深度”解題的內涵與意義

1. 何謂“深度”解題？

“深度”解題教學是解題活動的教學，而解題活動是一種思維活動. 不僅是獲得答案的過程，更是思路探求的過程. 那么，怎樣的解題是有“深度”的？有“深度”的解題過程不應該是對某一種解題技巧的靜態訓練，而應該是蘊含著數學思想方法的動態思考，數學方法論便是溝通二者的橋梁.

2. 如何“深度”解題？

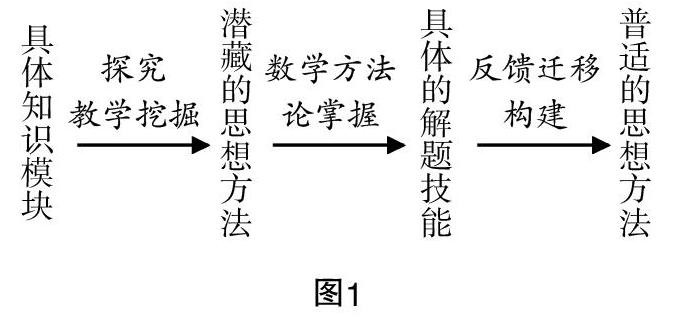
實際課堂教學中，教師往往先教授學生解決問題的技能并讓其反復訓練，學生熟練掌握后再告知方法中所蘊含的深刻數學思想. 從建構主義的觀點出發，這一過程顛倒了學生圖式建構的心理順序，學生在這一過程中并沒有經歷思想方法在認知結構內部的建構過程，它是由教師強加給學生的，因此這種思想方法并沒有轉化為學生的認知圖式.而思想方法作為數學教學的靈魂，數學解題教學也應該在數學方法論的指引下，建立如下“深度”解題教學的一般過程（圖1）：

3. 為何要“深度”解題？

首先，解題教學是訓練學生數學思維，培養問題意識、探究精神的最佳契機. 《普通高中數學課程標準（2017年版）》也指出：數學課程要注重發展學生的數學核心素養，學生學會用數學眼光觀察世界，用數學思維分析世界，用數學語言表達世界[2]. 而解題教學作為數學課程一部分，引導學生進行“深度”探究就顯得尤為必要. 其次，“深度”解題能夠引導學生理解數學，深刻認識數學的本質，總結大量的數學方法，揭示數學發現和創造的規則，從數學的發展方式中把握數學內在的本質和規律.

一個數學解題探究的教學案例

1. 數學方法論搭建解題技能與數學思想的橋梁

宏觀的數學方法論，著眼于數學思想;微觀的數學方法論，立足于具體的解題技能，而這一理論更是搭建解題技能與數學思想的橋梁.基于“深度”解題教學的一般步驟，本案例從學生非常熟悉的一道練習題出發，進行深入探究.請看案例第一部分：

例題：α為銳角，求證：■+■≥25.

師：這是一道平時常見的題目，我們已經做過很多次了.還記得怎么做嗎？

生1：這道題很簡單，在式子的左邊調整系數添上“1”，而cos2α+sin2α=1，展開后得出常數，再求■+■的最小值就可以了.

師：既然可以添上系數“1”，那么添上“2”“3”可以嗎？能不能想辦法添上“k”使它更具有一般性呢？

評析：以學生熟悉的習題為載體，基礎的數學方法為抓手. 面對此題，學生會主動思考“難道還有其他方法嗎？”在教師的引導下，激發學生的學習積極性，活躍課堂氣氛.

生2：聽了生1的方法，思考片刻后，認為可以運用k解決. （學生上臺板書）

板書：■+■=■+■+kcos2α+ksin2α-k=■+kcos2α+■+ksin2α-k≥4■+6■-k.

等號當且僅當■=cos4α，■=sin4α時成立，即■=cos2α，■=sin2α，代入sin2α+cos2α=1，解得k=25，此時10■-k=25，故■+■的最小值為25.

師：大家認同生2的做法嗎？（學生思考后全部同意）實際上，這是待定系數法的運用. 但添加的內容與生1大有不同，配湊上了“k”倍的“1”. 將一個涉及三角函數的不等式問題轉化為以k為變量的函數最值問題，最后只要通過等號成立的條件確定k的取值范圍即可.

評析：多數學生局限于單一的不等式知識模塊，認為這題只有生1的一種解法，而生2卻通過類比數學思想，聯想到待定系數法.這一環節立足于學生的最近發展區，由淺入深，由感性到理性，引導和幫助學生思考問題.數學思想與數學方法之間跨設的橋梁將這一看似平淡的解題課逐步引向了深度.

2. 數學方法論梳理解題過程中的思考脈絡

如何進行有“深度”的解題？學生能夠思考出第二種方法，已是本題教學的突破.然而，探究的腳步卻遠遠沒有停下. 請看案例的第二部分：

師：其實，這一題還可以將均值不等式法和待定系數法兩者結合起來.大家動手試一試！提示：同一個量用兩種方法進行表示，大家看看是哪一個量呢？

3：生2中出現了最值，想到設最值為S，用三角函數cos2α+sin2α=1表示同一個S，再求解不等式. （學生上臺板書）

板書：令S=■+■，得等量S=S·1=S（cos2α+sin2α），于是2S=S+S=■+■+S（cos2α+sin2α）=■+Scos2α+■+Ssin2α≥4■+6■=10■. 由2S≥10■，得S≥25.

師：非常好！（課堂氣氛頓時熱鬧了起來）這里依然體現了數學思想方法中的類比思想，還有化歸思想;也同時結合了均值不等式、待定系數法兩種不同方法. 可見，雖然這是一道簡單的作業例題，通過大家的不斷探究，發現可以用多種方法來解決問題.

評析：不少學生認為，一道數學問題的精妙解法只是“聰明人”一時靈光乍現的想法，可遇而不可求.這樣的認識無疑會打擊學生的探究精神.教師需要借助數學方法論，讓這一看似虛無縹緲的思維過程形成清晰明確的思考脈絡，使學生認識到再精妙的解法也是有路可尋的.

師：大家繼續看這一道題. 求證：■+■≥■. 以上方法都可以嗎？

生4：不等式左邊分母進行換元，之后的做法與前面一題一致.

師：不同的數學問題，不外乎是由條件和結論或所求目標構成. 在不同的條件背后，卻蘊含著相同的數學本質. 而我們所追求的是從熟悉的方法中萌生出更巧妙的方法.

通過引導學生掌握證明例題的兩種方法后，以例題的有效變式作為支撐，繼續深入探究生3的方法. （學生獨立思考）

題目1：已知x，y是正實數，且■+■=1，求證：x+2y≥3+2■.

題目2：已知x，y是正實數，且x+y=2，求證：■+■≥2.

題目3：已知x，y是正實數，且x+2y=3，求證：■+■≥3.

師：首先，很容易發現題目1可以用柯西不等式完成，那么題目2和題目3也可以嗎？其次，如果運用生3的方法，又會有怎樣的發現？接下來大家思考5分鐘，然后小組討論，談談各自的證明思路.

生5：我們小組發現，以上三個題目用生3的方法都可以證明.比如題目1，給我們的條件是■+■=1，和cos2α+sin2α=1有些不同，但是我們類比生3的方法，用待定系數法設出S=x+2y，又將S=S■+■表示，整個式子進行化簡，得到2S=S+S=x+2y+S■+■=x+S■+2y+S■，運用均值不等式可以得到2S≥2■+2■，解得S≥3+2■.

分析：奧蘇泊爾曾指出相比于宏觀上位的認知結構，下位而具體的技能方法更難進行水平遷移. 教師進行解題教學時如果就題論題，學生即便掌握了這一方法也很難做到舉一反三，在面對變式時仍將束手無策. 首先，教師必須以宏觀的數學方法論作為指引，將具體的技能教學上升到宏觀的思想方法教學，以此加強具體方法的可遷移性. 其次，教師要理解教學，對教學規律認識深刻，對教學問題要敏銳，看教學是否能引發學生的思考，鼓勵學生的創造性思維，培養學生良好的學習習慣和方法.

師：首先，對于你們組討論的結果表示肯定. 將不同的數學方法巧妙地結合在了一起.老師補充一點，這里還滲透了等價轉化的數學思想，同一個量用不同方法來表示. 其次，大家也很好地模仿了生3的證明過程，你就會發現其實這一題并不難了. 那么，對于題目2和題目3，你們是怎么想的？（小組討論后，生7和生8兩位學生上臺板書）

師：這兩位同學都完成得非常好！大家把掌聲送給他們！雖然題目2和題目3所給的條件等式不同，所證的不等式次數也不同，證明的方法卻是一樣的. 那么，我們是不是可以猜想它的一般情況呢？接下來讓我們嘗試對該類題型作出歸納.

分析：對母題進行推廣，學生通過對掌握的待定系數法進行遷移使用來重新體會化歸和類比歸納的思想，此時的思想是由學生在解題過程中由內向外生長出來的，因此學生在這個解題過程中經歷了化歸和類比歸納思想的建構過程.使得這一堂解題教學簡約而不失內涵，有序而又靈活.

3. 數學方法論升華解題結果的價值取向

一堂解題教學課中，學生關注的是解題結果的生成. 其實，獲得答案的本質也是發現與發明的過程. 基于數學方法論的引導，學生能夠揭示數學知識本質，并在其探究過程中滲透數學精神的同時，強調育人價值. 請看案例的第三部分：

題目4：（師提出）已知x，y是正實數，且x+λy=n，求■+■的最小值.

師：這一題是將條件和結論一般化.還可以用這一種方法來證明嗎？大家思考5分鐘，小組討論.

課堂上一片寂靜，許多學生對此題沒有思路.

師：大家能做到哪一步？

生9：設■+■=S，然后1=■■+■，x+λy=n，之后就做不下去了.

師：非常好！你做到這一步非常關鍵！接下來的證明由老師完成吧！（師板書）

板書：設■+■=S，■=1，得等量S=S■，于是

（1+n）·S=S+n·S=■+■+n·S■=■+■+■+■≥（n+1）■+（n+1）■=（n+1）（λ+1）■.

由（1+n）·S≥（n+1）（λ+1）■，得S≥（λ+1）■=■，即■+■≥■. 故最小值為■.

師：不難看出，將所論的具體數學問題，放在一般的狀態下進行思考，使得這一種新方法更具有一般性.從一個復雜的數學問題，聯想到與之相近的知識或類似的問題，并發現它們之間的內在聯系. 比如這道證明題，我們也是通過解決幾個具體的題目后才能夠解決.

分析：傳統意義上的解題，把“題”作為考察的對象，把“解”作為研究目的.在很多情況下，對“題”的關心，對“解”的追求，遠遠超過對“解題”本身的注意. 案例的前兩部分只是告訴了我們在精明的數學成果的背后，應用了什么樣的數學方法，得到了什么數學結論. 而案例的第三部分揭示了怎樣應用數學方法，如何發現更一般的數學結論. 達到了“既見樹木又見森林”的目的. 潛移默化地滲透了各種數學思想以及方法.

4. 課堂小結

師：經過這節課探究學習，大家有什么收獲？

生10：以例題證明作為切入點，引導我們通過待定系數法和均值不等式兩種方法的融合以及函數、等價轉化、化歸和類比歸納等數學思想來多角度看一道證明題. 并在此基礎上，引申出了3個題目，最后形成一般化的推廣.

師：這節課大家的思維很活躍，在大家的合作下，一連串的問題都解決了. 本文以一道常規的不等式證明題為例，進行探究，運用從特殊到一般、轉化等一些基本思想方法，反復強調轉化與化歸、類比歸納等數學思想方法的重要性. 題目從易到難，層層遞進. 希望大家在今后的學習中，能夠靈活運用這些數學方法，細細體會其中的數學思想！

基于數學方法論的“深度”解題過程中的兩個注意點

1. 以數學知識體系和蘊含的方法論分析為基石

人的思維依賴于必要的知識和經驗，數學知識正是數學解題思維活動的出發點與憑借. 豐富的知識并加以優化的結構能夠為題意的本質理解與思路的迅速尋找創造成功的條件. 例如，若能熟練掌握待定系數法和均值不等式等基礎知識的體系，深刻理解其數學本質，便能有對如上例題的“再創造”. 此外，數學知識體系的完善還要以其背后所蘊含的方法論作為基礎. 知識體系是靜態的、枯燥的，方法論讓它活了起來、動了起來，由靜態的知識轉化為動態的方法. 具體地說，學生雖然掌握了知識體系，熟悉基本的邏輯規則和常用的解題方法，卻找不到體系與實踐的聯系. 相反，若以方法論為腳手架，卻能夠起到會一題、通一類、達一片的教學效果.

2. 以數學思維作靈魂引領學生探究

數學是鍛煉思維的體操，高質量的數學學習以數學思維作為首要基礎. 通過對解題過程的探究分析形成一般意義的數學思維框架顯得極為重要. 本案例中，學生通過一個簡單的例題和熟悉的證法，發現了新的證法，并解決了一系列由例題引出的變式，加以推廣，足以體現數學思想方法在解題探索中的價值.由此可見，教師要充分發揮學生的主體性，引導學生形成由上述常規數學思維所組成的思維框架. 這將有助于學生舉一反三、觸類旁通，同時也使得學生思維本身不斷向更高層次發展[3].

總之，如何培養學生的思維能力是數學教育界關注的問題. 以數學方法論指引數學解題不是增設一門學習課，而是要求教師在每堂數學課中滲透數學思想方法以幫助學生形成解題的思考脈絡，養成長時間思考的能力和習慣. 這一過程不是一蹴而就的，需要教師時刻關注.

參考文獻：

[1]? 鄭毓信. 數學教育視角下的“核心素養”[J]. 數學教育學報，2016，25（03）.

[2]? 中華人民共和國教育部制定. 普通高中數學課程標準（2017年版）[M]. 北京：人民教育出版社，2018.

[3]? 戴經緯，唐恒鈞. 基于數學方法論的問題鏈——學生有脈絡地探索[J]. 中國數學教育，2018（20）.