農藥霧滴空間運行中的變形特征分析

馬學虎，薛士東，孫桐，奚溪，宋小沫，趙峻逸，蘭忠，郝婷婷

（遼寧省化工資源清潔利用重點實驗室，大連理工大學化學工程研究所，遼寧大連116024）

化學農藥在重大病蟲草害防控、保證國家糧食安全方面發揮著不可替代的作用，合理使用農藥有助于提高農業生產力和保障農作物質量，使用農藥可減少全球高達45%的糧食損失[1]。據國家統計局數據顯示，2014 年中國農藥的使用量為180.69×104t，但是由于噴霧技術和噴霧管理的限制，農藥的利用率僅為20%～30%[2]。

農藥的使用過程一般分為以下幾個步驟[3-4]：①藥液通過噴頭完成霧化過程；②霧滴在空氣中運動擴散，沉積到靶標冠層或飄失到靶標外；③霧滴在冠層表面撞擊、鋪展；④霧滴被冠層表面吸收，傳導到為害部位并發揮藥效。根據ISO 22856 標準所定義，霧滴飄移是指“在施藥過程中，農藥霧滴被氣流攜帶脫離靶標冠層、流失到地面或者懸浮在大氣中的行為”，被認為是導致農藥污染的“罪魁禍首”，對周圍河流中的水生動植物、大氣環境、人類身體健康造成不可扭轉的危害[5-10]。霧滴飄移是諸多因素共同作用的結果，包括藥液的理化性質、霧滴的粒徑及分布、作物結構（排與排的間距、冠層結構、冠層穿透性）、操作條件（噴霧流量、操作壓力、農機行駛速度）、氣候條件（風速、風向、溫度、濕度）等[11-18]。

研究霧滴飄移的手段主要包括風洞試驗、田間試驗、數值模擬等。在風速可調、溫濕度可控的低速風洞中，研究噴頭類型、操作壓力、助劑種類等對霧滴群飄移比例的影響[19-21]。在田間試驗中，通過檢測靶標冠層內示蹤劑的含量來評價霧滴群的飄移沉積比例[22-24]。在數值模擬中，采用歐拉-拉格朗日離散相模型追蹤霧滴群的運動軌跡，從而獲得特定條件下霧滴群的飄移率[25-27]。

以往的數值模擬研究中多將農藥霧滴視為不會發生形變的剛性顆粒，忽略了霧滴的形變過程。在霧滴撞擊靶標和界面蒸發的研究中也多以完美球狀作為霧滴的初始狀態[28-30]。然而大量研究表明，霧滴形狀對霧滴的聚并與破碎、靶標撞擊、所受的曳力大小等都有著重要作用，會直接影響霧滴的飄移損失與界面流失等。QUAN 等[31]利用耦合了移動網格相界面追蹤的三維有限體積交錯網格法模擬了液滴在加速氣流中的運動情況，分析了液滴的形變狀態及附近氣流的速度場變化。結果表明，變形過程中液滴的非穩態曳力總是比同等雷諾數下液滴的穩態曳力大，同時降低表面張力和黏度會增大液滴的形變量，導致曳力增加，而密度比對液滴動力學影響不顯著。QU 等[32]用ANSYS Fluent 軟件對非對稱流中的減速液滴進行模擬，結果表明隨著We 的增大，液滴的形變量及曳力會急劇增大，振蕩周期延長；隨著Oh 的增大，形變量與曳力略有增大而振蕩周期幾乎不變。

目前針對單個農藥霧滴在風場中的運動研究鮮有報道，尤其是對微米或者亞毫米級別農藥霧滴的空間變形特征更是缺乏研究。單霧滴是構成霧滴群的基礎元素，明晰單霧滴的運行飄移規律，對于深入研究整個霧滴群的運動規律具有重要的指導意義。因此本文以農藥噴霧中的單霧滴為研究對象，采用數值模擬的手段研究了霧滴在橫向風場中的空間形變特性，揭示了不同因素作用下單霧滴的形態演化規律，并建立了多因素協同下霧滴形變量與形變周期的預測模型。

1 數值模擬計算模型與方法

1.1 幾何模型

基于COMSOL Multiphysics 5.2建立數值模擬過程，選擇帶相初始化的層流-水平集物理場，對氣液相界面進行追蹤，獲得霧滴的空間形變特性。如圖1 所示，針對直徑為100μm 的霧滴，選取1200μm×300μm二維矩形計算域，霧滴的初始位置坐標為(100μm，1100μm)。計算域的尺寸隨著霧滴的大小進行相應調整，以保證計算域的合理利用并盡可能降低計算成本。

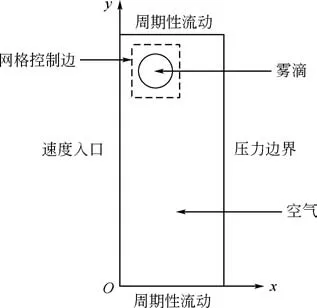
圖1 幾何模型

1.2 控制方程及邊界

對含有分界面的不可壓縮、不混溶的氣液兩相流動系統進行模擬時，關鍵問題在于如何將界面離散化并且準確地追蹤界面的演化過程。Level Set方法通過設置一個距離函數隱式追蹤自由面，并且將界面條件融入控制方程中，可在整個域內用統一的差分格式進行求解。與移動網格方法和相場方法相比，可以避免顯式地追蹤界面，不需要進行復雜的界面重構，可方便地追蹤界面的拓撲結構改變，兩相控制方程組如式(1)、式(2)所示。

連續性方程

Navier-Stokes方程

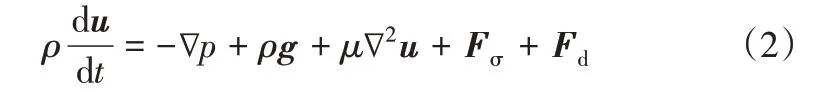
式中，Fσ為單位體積流體所受的表面張力；Fd為單位體積流體所受的曳力。由于氣相密度遠小于液相密度，因此忽略霧滴所受浮力的作用。

霧滴在橫向風場中所受的曳力大小如式(3)所示。

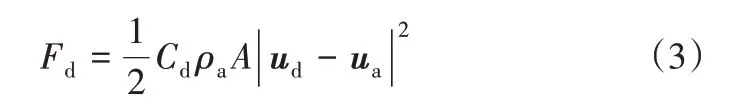
式中，A為霧滴在風向上的投影面積，在二維計算中降維為投影長度；ud為霧滴在空間某一位置處的速度矢量；ua為相應位置處空氣的速度矢量；Cd為曳力系數，計算依據選取文獻[33]中提供的農藥噴灑過程中霧滴雷諾數在0.25＜Re＜104范圍內的經驗公式，如式(4)所示。所受曳力方向與霧滴的相對運動方向相反。

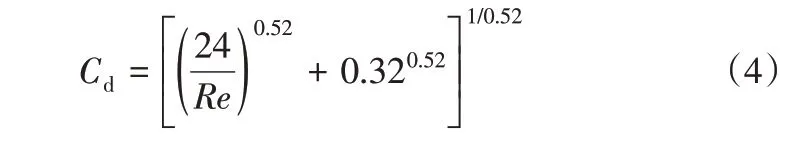
表面張力可以在整個計算域中連續求解，表達為一個光滑函數的形式，見式(5)。

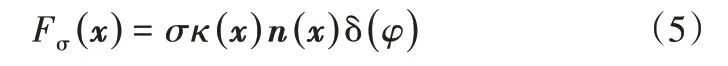
其中，κ為相界面曲率，其值見式(6)。

n為氣液相界面法向向量，其值見式(7)。

φ為經Heaviside函數平滑后的水平集函數，代表網格內空氣相的體積分數，其在界面一側的值恒為1，另一側恒為0，在相界面很小的寬度內由1過渡到0。分別求解各相內的流體物性，在相界面處借助水平集函數對物性參數進行定義，使物性在界面處得以連續。計算過程見式(8)、式(9)。

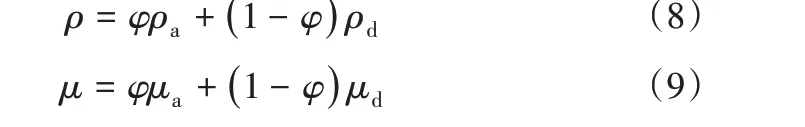
δ表示規整后的delta函數，其值見式(10)。

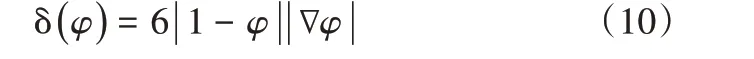
δ為一維Dirac函數，通過δ可將邊界上的積分改寫為體積上的積分。δ只在相界面附近有值，從而使表面張力的作用限定在界面處。

1.3 邊界條件

二維矩形計算域的左側設置為速度入口，如式(11)。

右側邊界為壓力出口，與大氣連通，如式(12)。

上下邊界定義為周期性流動條件，以減小計算域的面積，縮短計算時間，減少占用內存。域內空氣初速度大小等于其入口速度ud,0，霧滴在初始化位置具有豎直向下的初速度，如式(13)。

本文中所有算例霧滴的初速度設定為10m/s[34]。

1.4 網格劃分

為提高網格規整度，防止液滴初始化導致的網格不規則分布，使用網格控制邊對計算域分區，在各子域內劃分網格，如圖1中虛線所示。霧滴初始化位置四周使用自由三角形網格，余下區域應用較規整的四邊形單元map網格，以提高計算精度并減少所需計算資源。本模擬中通過設置網格最大單元尺寸和最小單元尺寸，在COMSOL 中自動進行網格的生成，計算前進行網格無關性檢驗，以優化網格的劃分。

1.5 后處理

通過霧滴在空間運行中的軌跡變化來判斷網格選擇的合理性，需要得到不同時刻霧滴的位置。如圖2所示，將計算得到的體積分數圖像用MATLAB進行編程處理，將圖像轉化為二值圖像，提取相界面的輪廓。通過計算輪廓各點坐標的均值可獲得各個時刻霧滴的質心坐標，從而連成霧滴的運動軌跡。

霧滴在空間運行中會由球狀變成橢球狀，為了描述霧滴在橫向風場中下落時的形態演化規律，定義霧滴的形變比E=b/a，其中a 代表橢圓長軸的長度，b代表橢圓短軸的長度。定義霧滴的形變量為e=1-E，當霧滴呈現球狀時e=0，橢球狀時0＜e＜1。

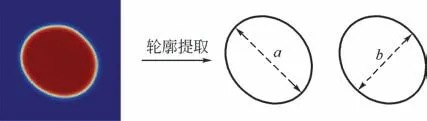
圖2 后處理過程

2 結果與討論

2.1 網格無關性驗證

以直徑為100μm 的霧滴為例，設定最小及最大單元尺寸自動劃分網格。霧滴下落是一個瞬態過程，以霧滴在0.1ms內的運動軌跡及速度變化作為評價指標來驗證網格無關性，結果如圖3所示。

當網格數達到45569時，再提高網格精度對霧滴的軌跡及速度影響不大，可認為該網格精度足夠高，具有較好的計算性價比。此時網格最大單元尺寸為3μm，最小為0.01μm。所有算例的域內最大速度基本一致，對不同尺寸的霧滴選取相同的網格劃分精度，保證了所有霧滴都具有相同的界面厚度。

2.2 霧滴空間形變過程

具有向下初速度的霧滴在左側來流橫向風中運動的形態演化過程，如圖4所示。霧滴在一個振蕩周期Δtd內經歷了“最初的球→橢球→球→橢球→球”的形變過程，橢球長軸方向與豎直方向有一定的夾角。霧滴由起始時刻的球形變為橢球狀再回到球形的這一過程簡稱為“初次變形”，所經歷的時間記為Δt1；繼而再由球形變為橢球到振蕩周期結束這一過程簡稱為“二次變形”，所經歷的時間記為Δt2，Δtd=Δt1+Δt2。霧滴受到左側來流橫向風的作用，同時自身具有向下的初動能，在霧滴下緣產生一個低壓區，從左側來流的橫向風更容易進入霧滴下側，氣流對霧滴產生剪切作用，使霧滴形變為長軸偏向上風向的橢球形。隨著霧滴不斷下降，霧滴的形狀逐漸變為具有較大曲率的橢球形，導致霧滴的表面張力增大，逐漸增大的表面張力與曳力相平衡使得形變程度慢慢減弱，在一段時間后幾乎又恢復到球狀，但由于霧滴的形變仍在繼續，二次形變中霧滴的拉伸與壓縮方向與第一次相反，曳力的阻礙作用導致形變程度相對于第一次發生了衰減。隨著霧滴繼續下落，再一次恢復到近似球狀，至此一個振蕩周期結束。

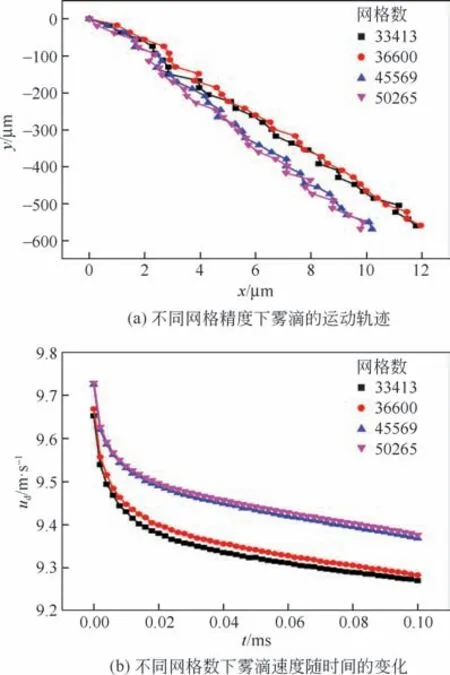
圖3 網格無關性驗證(ua=3m/s;μd=1.0mPa·s;σ=72.7mN/m)

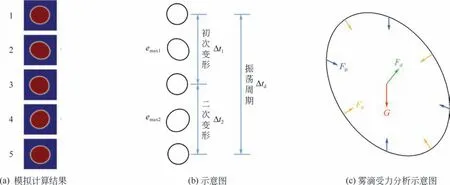
圖4 150μm的霧滴在橫向風中運動的形變過程

霧滴在橫向風場中運動的形變過程是多種因素共同作用下的結果。如圖5所示，為不同條件下霧滴達到最大形變量時的形態特征。下面依次討論霧滴直徑、橫向風速、藥液的理化性質等對霧滴形變特性的影響。

圖5 不同條件下霧滴達到最大形變量的計算結果圖

2.2.1 霧滴直徑對霧滴形變的影響

根據美國農業工程師學會（ASAE）對農藥霧滴尺寸的分類標準，取直徑為100μm、150μm、200μm、250μm、300μm 的細霧滴、中等霧滴、粗霧滴，將它們置于速度為3m/s的橫向風場中，液相黏度為1.0mPa·s，表面張力為72.7mN/m。考察霧滴直徑對空間形變特性的影響，結果如圖6所示。

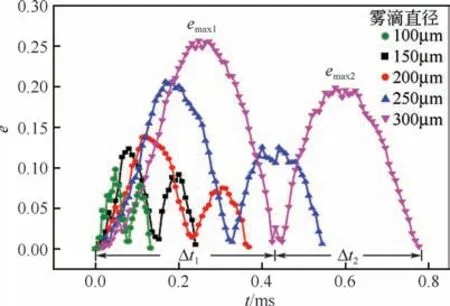
圖6 不同直徑霧滴在橫向風場中形變量e隨時間的變化

結果表明，霧滴的振蕩周期Δtd和形變量e 均隨著直徑的增大而增大。當直徑增大時，霧滴的重力和曳力均會增加，在與黏性力及表面張力的競爭中取得優勢，保持原有運動狀態的趨勢增強，霧滴形變的周期會延長，同時霧滴自身重力的提高會增大形變程度。在一個振蕩周期Δtd內，形變量的第二個峰值小于第一個峰值emax1＞emax2，同時有Δt1＞Δt2，表明振蕩形變發生了衰減。一方面是由于霧滴在下落過程中速度減慢，在一定程度上抑制了形變過程；另一方面是由于氣流方向向右，空氣對霧滴的拖拽作用總是沿著左上右下這一方向，使得霧滴在此方向上被拉長得更多。另外可以發現，霧滴從橢球變為球的時間略短于從球變為橢球的時間，這是因為對于橢球而言，由于它發生了形變，在風的投影方向長度拉長，空氣給予橢球霧滴的曳力要大于球形霧滴，所以在霧滴呈現橢球形時速度衰減更快，形變也就更快。

2.2.2 橫向風速對霧滴形變的影響

取直徑為100μm、液相黏度為1.0mPa·s、表面張力為72.7mN/m 的霧滴，分別將其置于橫向風速為1m/s、3m/s、5m/s、7m/s的穩定氣流場中，考察橫向風速對霧滴形變特性的影響。

如圖7 所示，為霧滴形變量e 隨時間的變化情況。隨著橫向風速的增加，霧滴的形變程度也呈現增大的趨勢。霧滴受到空氣的曳力作用而發生形變，曳力大小與氣液相對速度呈正相關，風速越大意味著空氣拖拽霧滴的能力越強，形變越強烈。尤其當風速達到7m/s 時，形變量有明顯提升，第一次形變幅值emax1達到了風速為5m/s時的1.6倍左右，第二次形變幅值emax2達到了5m/s 時的1.2 倍左右。此外，分析霧滴的振蕩周期可以發現，隨著風速的增大，Δt1、Δt2和Δtd幾乎不發生改變，即4 種情況下霧滴的振蕩周期都為1.32×10-4s，達到第一個形變峰值的時間都在0.048ms左右。結果表明，霧滴的振蕩周期受橫向風速的影響不明顯，振蕩周期為一個本征量，由霧滴自身特性決定。

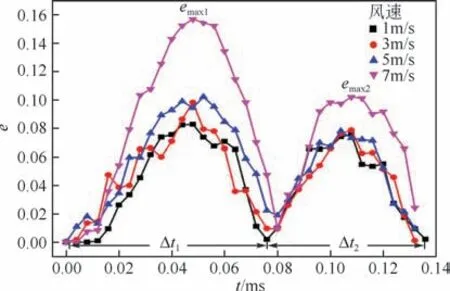
圖7 直徑為100μm的霧滴在不同橫向風場速度下形變量e隨時間的變化

2.2.3 液相黏度對霧滴形變的影響

液體的黏度反映出流體內部的黏性效應，黏度越大的液體表明其內部的凝聚力越大，因此黏度的大小勢必影響著霧滴的形變程度。考察霧滴初始直徑為150μm，橫向風速3m/s，表面張力為72.7mN/m，液相黏度分別為0.3mPa·s、0.5mPa·s、1.0mPa·s、2.0mPa·s時，霧滴的空間形變特性。

如圖8所示，隨著液相黏度增大，霧滴的形變量減小，但振蕩周期Δtd沒有明顯的變化，說明霧滴的振蕩周期與液相黏度幾乎無關。當液相黏度為0.3mPa?s 和0.5mPa?s 時，Δt1與Δt2幾乎相等，各占一個完整周期的一半，同時霧滴的振蕩幅度也沒有衰減，兩次形變量最大值幾近相同。然而當液相黏度為1.0mPa?s 和2.0mPa?s 時，emax1＞emax2，Δt1＞Δt2，形變程度發生了衰減。分析原因認為，當液相黏度較大時，霧滴的形變主要由兩相間的剪切作用決定，故前半周期比后半周期長；而當液相黏度較小時，內部凝聚力小，為影響形變的主導作用，形變的衰減現象不再顯著。此外，黏度較小的霧滴在第一個振蕩周期結束時難以恢復到近球形，黏度越小這一趨勢越明顯，這是由于霧滴自身的黏度較小，內聚力較弱，在運動過程中難以與曳力相抗衡，很難恢復到最初的形狀，只能維持一定的形變量在空氣中繼續運動。

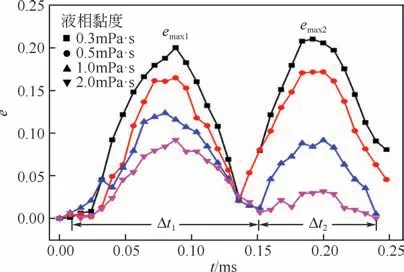
圖8 不同黏度的150μm霧滴在橫向風場中形變量e隨時間的變化

2.2.4 表面張力對霧滴形變的影響

根據文獻[16,35-36]報道，按照一定的配比添加不同種類的助劑可以調控霧滴的表面張力在20～73mN/m 之間，在田間實際操作的范圍內。考察霧滴直徑為150μm，橫向風速為3m/s，液相黏度為1.0mPa·s，表面張力分別為28.5mN/m、37.4mN/m、56.9mN/m、72.7mN/m時空間形變特性。

根據能量最低原理，在氣液相界面處的液相表面分子會自發趨向于液相內部而非表面，這使得表面張力對塑造霧滴形態起著十分關鍵的作用[37]。如圖9所示，不同表面張力下霧滴的形變規律與前述算例相同，形變幅度逐漸衰減（emax1＞emax2），形變時間逐漸縮短（Δt1＞Δt2）。當液相表面張力較小時，在與曳力、重力的競爭中處于弱勢地位，霧滴恢復到表面能較低的球形狀態更加困難，從而延長了霧滴振蕩形變周期，增加了形變幅度。無論是前半個周期結束時還是整個振蕩周期結束時，表面張力越小的霧滴越難以恢復到初始的球形，如表面張力為28.5mN/m的霧滴在0.392ms時完成整個振蕩周期，此時形變量仍有0.111，呈現出長軸與水平方向的橢球狀，這一點與低黏度的影響結果較為相似。

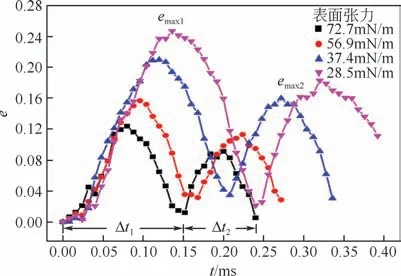
圖9 不同表面張力的150μm霧滴在橫向風場中形變量e隨時間的變化

2.3 霧滴形變預測關聯式

本文中影響霧滴空間變形特征的因素有霧滴直徑、環境風速、霧滴黏度和表面張力，并將霧滴的空間形變歸結于重力、曳力、黏性力和表面張力的共同作用。而Re 表征慣性力與黏性力之比，其中慣性力反映出霧滴速度對空間形變過程的影響，同時霧滴與空氣的相對速度又影響著曳力，因此曳力對形變過程的影響可通過慣性力進行描述；We 表征慣性力與表面張力之比；Oh 表征黏性力與表面張力之比。結合本文中影響霧滴空間形變的物理參數以及上述量綱為1 參數的意義，選擇了韋伯數We、奧內佐格數Oh和雷諾數Re的關聯式對形變量和形變周期作出預測。計算公式分別見式(14)～式(16)。

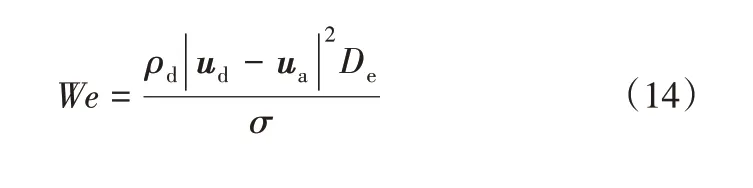
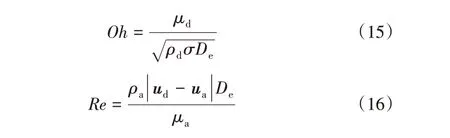
其中，當量直徑De選取為霧滴的初始直徑，ud和ua分別為霧滴的初始速度和橫向空氣速度。經過計算后，擬合所涉及的量綱為1 數范圍依次為：138.874＜We＜573.466， 66.730＜Re＜207.950，2.873×10-3＜Oh＜1.916×10-2。

采用多元非線性回歸方法對計算結果進行擬合，結果如式(17)所示。

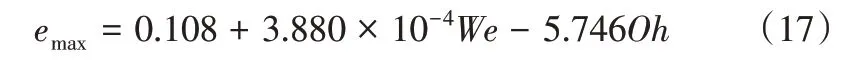
其中確定系數R2= 0.9497，如圖10 所示對比分析了回歸模型的結果與實際模擬的結果，霧滴形變量預測模型的平均相對偏差為8.40%。霧滴的最大形變量與液相黏度和表面張力呈負相關，說明液相黏性力和表面張力能夠阻礙霧滴形變，使其維持原有形態，而最大形變比與相對速度和初始直徑呈正相關，反映出曳力與重力對形變的增強作用。擬合分析結果與上文討論結果基本一致。

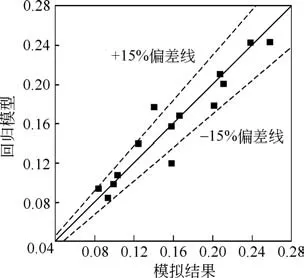
圖10 霧滴形變量模擬結果與回歸模型的偏差比較

同時，對初次形變時間占一次振蕩形變周期的比例（Δt1/Δtd） 進行擬合，得到如下結果，見式(18)。

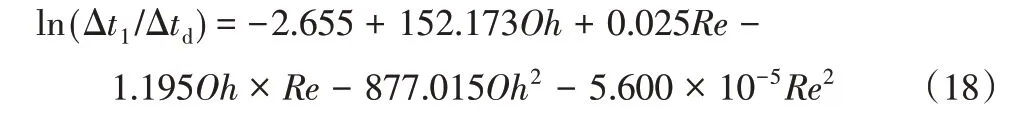
其中確定系數R2=0.9150，如圖11 所示，對比分析了回歸模型的結果與實際模擬的結果，該預測模型的平均相對偏差為5.83%。當霧滴特征參數及環境風速已知時，可以通過式(17)和式(18)分別預測出霧滴的最大形變量和形變周期，以此明晰霧滴的空間形態演化規律，為提出霧滴群的減飄手段奠定理論基礎。

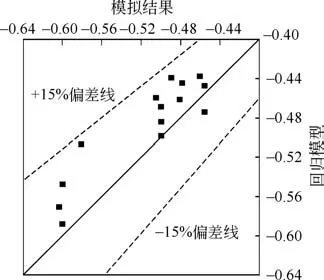
圖11 霧滴初次形變時間占比模擬結果與回歸模型偏差比較

3 結論

通過數值模擬手段對多因素耦合下單霧滴的空間形態演化過程進行研究，結論如下。

（1）霧滴在下落過程中的形變存在振蕩周期，且形變會發生衰減。霧滴的尺寸嚴重影響著振蕩周期和幅度，直徑越大，霧滴的重力和曳力越大，形變周期越長，形變幅度越大；橫向風速幾乎不改變形變周期，但風速增大會加劇霧滴形變程度；霧滴黏度主要影響形變程度，黏度越小，形變程度越大，同時在低黏度下霧滴完成一個形變周期后難以恢復到初始的球形，只能保持橢球狀繼續運動；表面張力值增大導致形變周期縮短，形變程度減弱，當表面張力很小時霧滴也難以恢復球形。

（2）霧滴的形變量受霧滴直徑、橫向風速、藥液黏度、表面張力等因素的共同影響，即形變量是一個由重力、曳力、黏性力及表面張力共同作用的結果；曳力和重力促使霧滴發生形變，而黏性力和表面張力阻礙霧滴發生形變。

（3）通過回歸分析得到的霧滴形變量與形變周期的量綱為1預測模型，可以計算出霧滴的空間形變量及形變周期，可明晰霧滴的空間形態演化規律，為提出農藥的減飄手段奠定理論基礎。

符號說明

A—— 霧滴在風向的投影長度，m

a—— 橢圓長軸，m

b—— 橢圓短軸，m

Cd—— 曳力系數

De—— 霧滴的當量直徑，m

E—— 形變比

e—— 形變量

emax1—— 第一個振蕩周期內，初次變形過程的最大形變量

Emax2—— 第一個振蕩周期內，二次變形過程的最大形變量

Fd—— 單位體積霧滴所受曳力，N/m3

Fσ—— 單位體積流體的表面張力，N/m3

g—— 重力加速度，m/s2

n—— 相界面法向向量

Oh—— 奧內佐格數

p—— 單位體積壓力，N/m3

patm—— 大氣壓，Pa

pout—— 出口壓力，Pa

R2—— 擬合相關系數

Re—— 雷諾數

u—— 流體的速度，m/s

ua—— 空氣的速度，m/s

ua,0—— 空氣的初始速度，m/s

ud—— 霧滴的速度，m/s

ud,0—— 霧滴的初始速度，m/s

uin—— 入口速度，m/s

We—— 韋伯數

x—— 到相界面距離，m

Δt1—— 第一個振蕩周期內，初次變形時間，s

Δt2—— 第一個振蕩周期內，二次變形時間，s

Δtd—— 第一個振蕩周期，s

δ—— Delta函數

κ—— 相界面曲率

μ—— 流體黏度，Pa?s

μa—— 空氣的黏度，Pa?s

μd—— 霧滴的黏度，Pa?s

ρ—— 流體的密度，kg/m3

ρa—— 空氣的密度，kg/m3

ρd—— 霧滴的密度，kg/m3

σ—— 表面張力，N/m

φ—— 水平集函數

下角標

a—— 空氣相

d—— 霧滴相

max—— 最大值