一個R2 上含雙曲函數核的Hilbert 型不等式

有名輝，孫霞

（浙江機電職業技術學院 數學教研室， 浙江 杭州310053）

0 引 言

Ω 為實數集R 中的L可測集,θ(x)是定義在Ω上的非負L可測函數,p＞1,

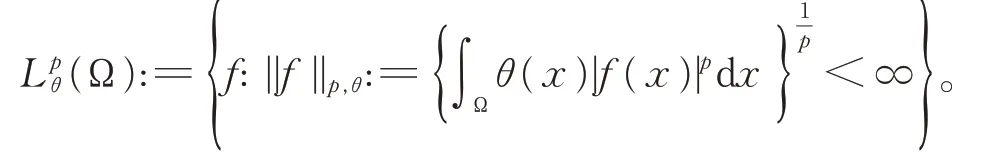
特別地, 當θ(x)=1 時, 上式可簡記為Lpθ(Ω)=Lp(Ω)。

若f,g≥0,f,g∈L2(0,∞), 則 有 以 下 著 名 的Hilbert 不等式[1]:

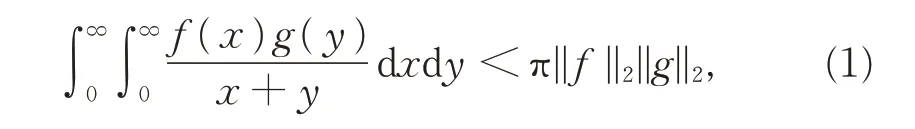
其中π 是滿足式(1)的最佳常數因子。

自提出Hilbert 不等式以來的100 余年中,通過對核函數(x+y)-1的演化、類比和推廣，加上其對應的離散及半離散形式，已建立了大量類似于式(1)的Hilbert 型不等式[2-9]，這些不等式在分析學中已有廣泛的應用[10]。

文獻[11-14]研究了以雙曲函數為核函數的Hilbert 型不等式，其中,文獻[11-12]分別建立了不等式：

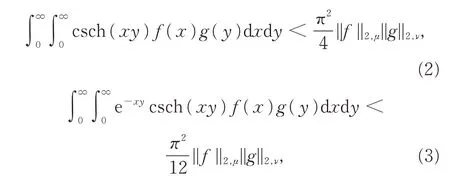
在式(2)和式(3)中, 均有μ(x)=ν(x)=x-3。

顯然，不等式(2)和(3)的積分核函數在R2中不恒為正, 不宜做全平面推廣。考慮到當α,β＞0 時,sinh(αt)與csch(βt)在實數域R/{0}上同號，故筆者探究全平面上核為sinh(αxy)csch(βxy)的二重積分不等式，并借助正切函數的有理分式展開,建立最佳常數因子與正切函數偶數階導數相關聯的Hilbert 型不等式。

1 定義及引理

定義1[15]對u＞0，定義第二型歐拉積分，即Γ函數：

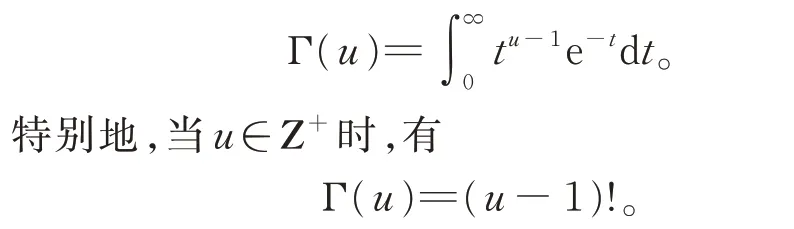
引理1 設|a|＜1，n∈N，φ(t)=tant，則

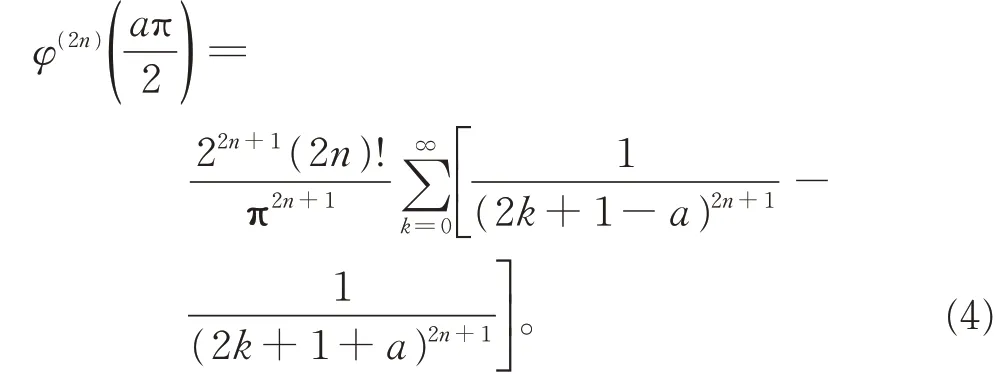
證明φ(t)=tant的有理分式展開如下[15]：

引理2設β＞α＞0,λ≥0,

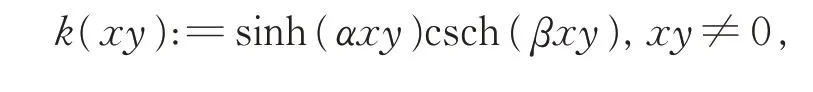
將csch(βt)展開成無窮級數，可得

通過簡單的代換，易得

將式(16)代入式(9)，可得式(7)。

類似地，可得式(8)。

證畢！

引理3,β＞α＞0,λ≥0,k(xy)及C(α,β,λ)由引理2 定義, 函數fε(x)和gε(x)(ε為充分小的正數)定義如下：

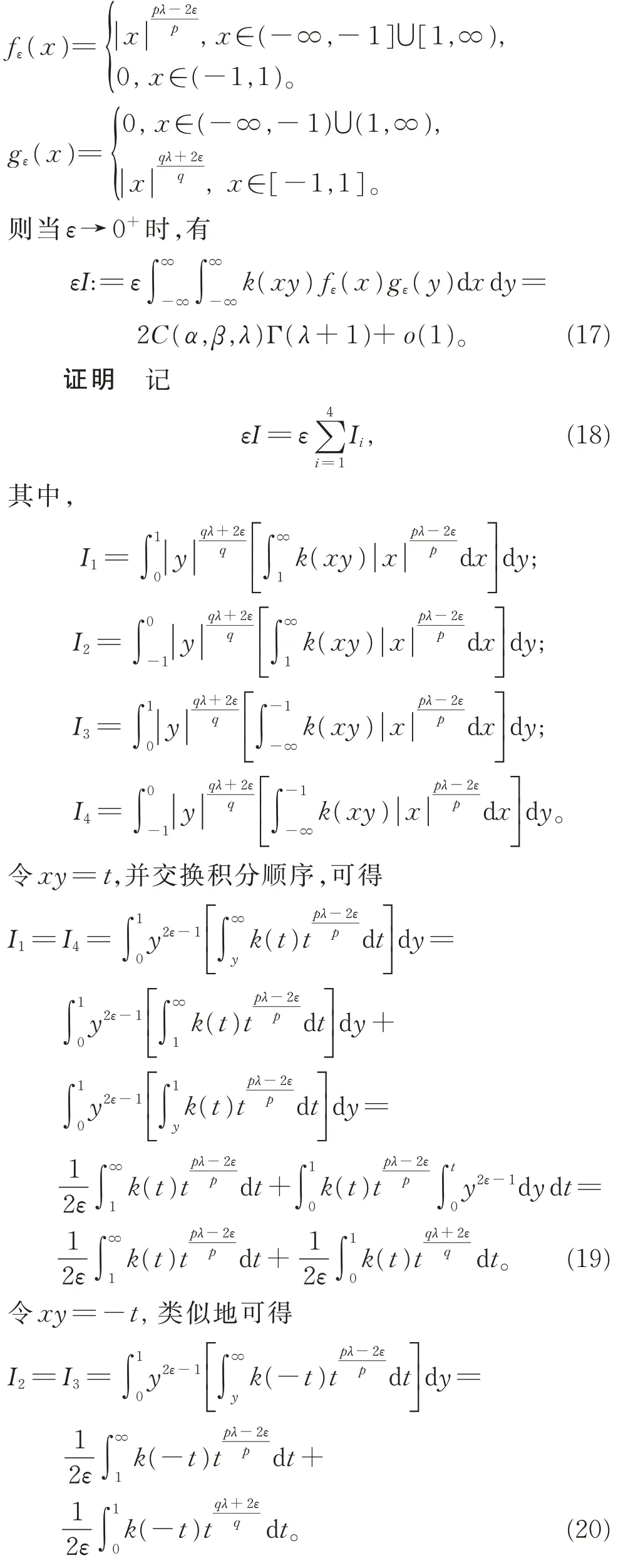
將式（19）和式(20)代入式(18)，可得

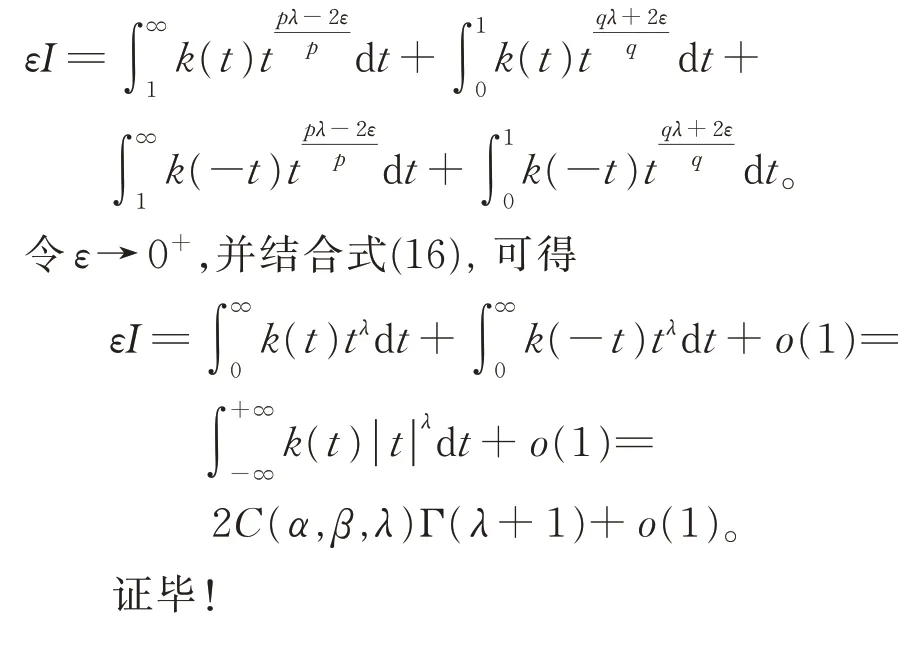
2 主要結果及證明

定理11，β＞α＞0,C(α,β,λ)如引理2 定義,λ≥0,φ(x)=tanx,n∈N,

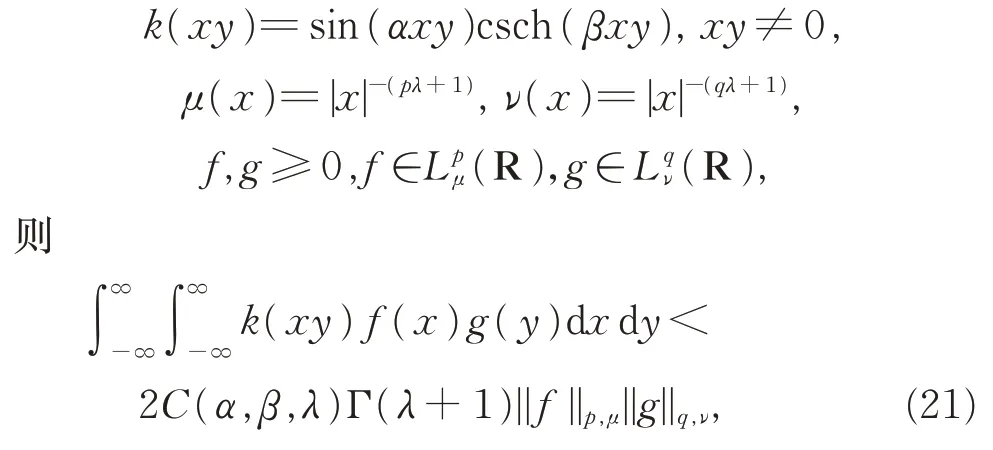
特別地, 當λ=2n時, 式(21)可轉化為

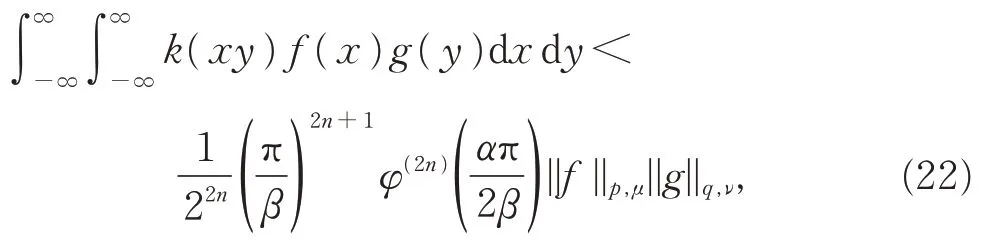
證明由H?lder 不等式，結合引理2，得

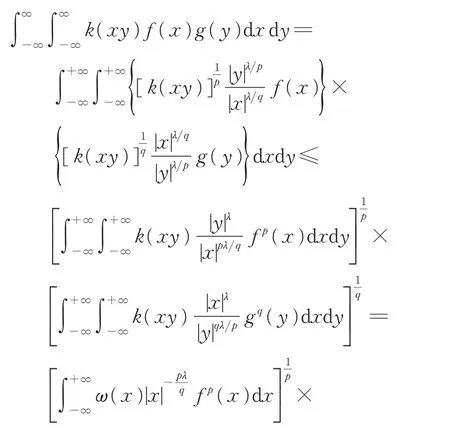
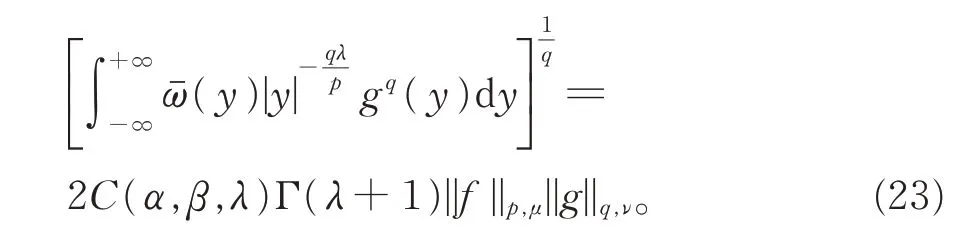
如果式(23)取等號，那么有不全為零的實數A1與A2,滿足

與f∈(R)矛盾。故式(23)取嚴格不等號。

下證式(21)中的常數因子2C(α,β,λ)Γ(λ+1)為最佳值。事實上，若此常數因子不為最佳值，則必存在更優實數k(0 ＜k＜2C(α,β,λ)Γ(λ+1))，使得式(21)中的常數因子替換為k后不等式仍成立。即

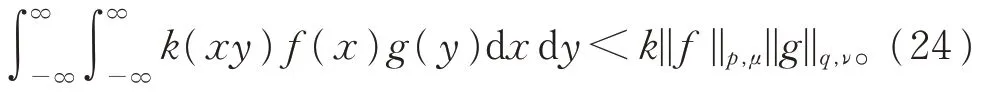
用引理3 中定義的fε和gε分別替代式(24)中的f和g，則有

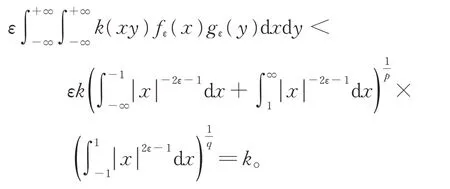
將 引 理3 的 結 果 代 入 上 式,并 令ε→0+，則 有k≥2C(α,β,λ)Γ(λ+1),矛盾。因此式(21)中的常數因子為最佳值。

特別地, 當λ=2n時, 根據引理2 中C(α,β,λ)的定義以及引理1 的結論, 不難得到式(22)。

定理1 證畢。

在定理1 中,令β=2α,λ=1, 并注意到

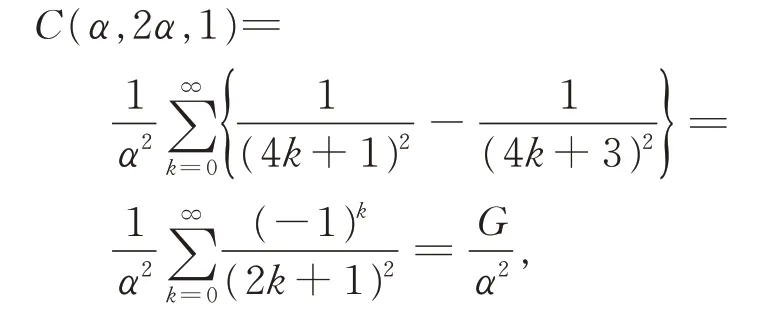
其中G=0.915 965 59…，為Catalan 常數。由此不難得到以下推論。

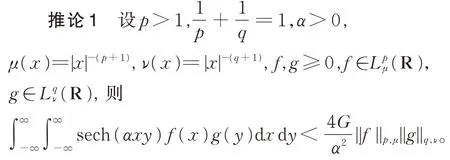
在定理1 中,令β=2α,λ=2n,由式(22)，又可得到另一個核為雙曲正割函數的Hilbert 型不等式。

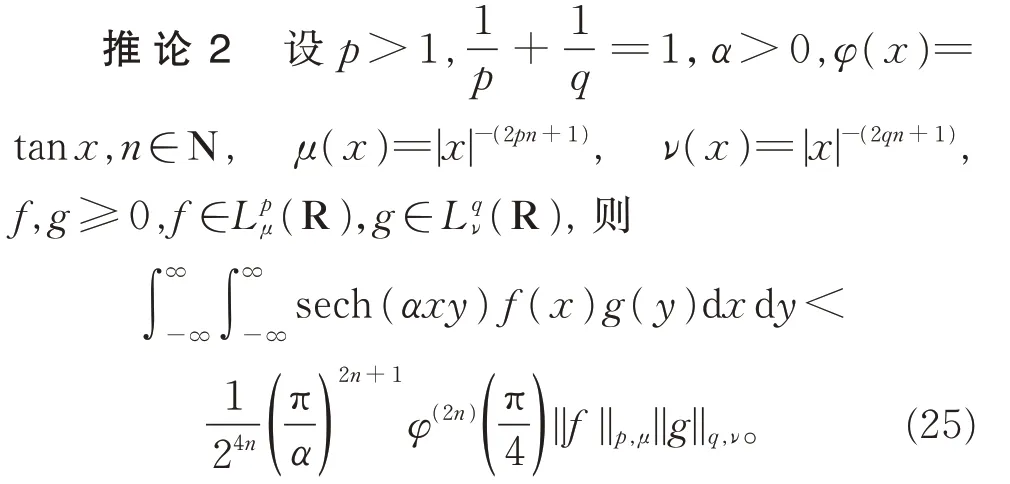
特別地, 若α=1，n=0，則μ(x)=ν(x)=|x|-1, 此時式(25)可化為

特別地, 若α=1，n=0，則μ(x)=ν(x)=|x|-1, 注意到tan=-1，此時式(26)可化為

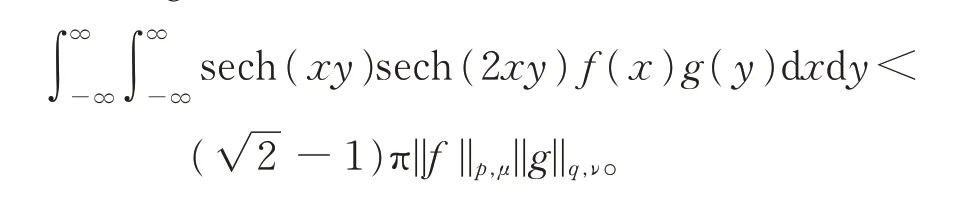
此外, 令β=3α,β=,…,還可得到一些很容易計算常數因子的Hilbert 型不等式，在此不一一贅述。