浙江大學函數論學派1928—1950 年的學術貢獻

薛有才，劉煒，彭佳

（1.浙江科技學院理學院，浙江杭州310023； 2.浙江特殊教育職業學院，浙江杭州310023）

0 引 言

浙江大學數學學派是民國時期形成的以陳建功、蘇步青等為代表的我國著名數學學術團體之一。該團體在函數、微分幾何、代數、數學史等領域做出了巨大貢獻。本文主要以其在傅里葉級數方面的工作來討論浙江大學函數論學派在1928—1950年的貢獻，以使讀者了解他們所做的工作。

傅里葉級數（Fourier series）是一種特殊的三角級數，由法國數學家傅里葉（J.B.J. Fourier）提出并發展為著名的傅里葉級數理論。我國現代數學的先驅陳建功、王福春、周鴻經、盧慶駿、徐瑞云、程民德、項黼宸等為傅里葉級數在我國的傳播與研究做出了巨大貢獻。其中，貢獻最大的是陳建功，他在1928年發表著名論文：On the class of functions with absolutely convergent Fourier series[1]，其中關于三角級數在區間上絕對收斂的充分必要條件被譽為“陳-哈代-李特爾伍德定理”，這是我國現代數學取得的第一個具有世界水平的成果，標志著我國現代數學開始向世界水平沖擊。數學家李仲珩于1947 年在總結我國現代數學發展時指出：“走分析這條路，是陳建功和熊慶來兩位領導起來的。其中成就最大的要算傅里葉級數的研究者，尤以王福春為難能可貴。”[2]

1 傅里葉級數在我國的研究概況

1.1 研究論文

據不完全統計，1928—1950 年，我國學者在國外學術期刊上發表的傅里葉級數相關學術論文共93 篇，在國內學術期刊上發表的相關學術論文有34篇[3-5]。其中，在國外學術期刊上發表論文的作者有10 人，分別為陳建功21 篇，王福春34 篇，程民德15篇，盧慶駿9 篇，周鴻經8 篇，徐瑞云2 篇，項黼宸、馮乃謙、朱良璧、周懷衡各1 篇；在國內學術期刊上發表論文的作者有12 人，分別為陳建功7 篇，程民德6篇，項黼宸5 篇，周鴻經3 篇，王壽仁3 篇，王福春2篇，盧慶駿2 篇，魏德馨2 篇，吳有訓、王季同、曾炯、范會國各1 篇。涉及傅里葉級數研究的作者共16人，國內外發表論文127 篇。其中，屬于浙江大學函數論學派的研究者有10 人，共發表論文109 篇。

此間，我國學者在國外發表數學學術論文共910 篇，參與工作的作者147 人。如此，傅里葉級數研究論文占比為11.41%，學者占比為8.61%；而浙江大學函數論學派在國外發表傅里葉級數相關學術論文共84 篇，占國外傅里葉級數相關論文發文總數的90.32%，占數學學科國外發文總數的9.23%；國內發表傅里葉級數相關論文25 篇，占國內傅里葉級數相關論文發文總數的73.53%。

1.2 研究專著

1929年，陳建功以傅里葉級數系列研究成果成為在日本取得理學博士學位的第一位中國學者。他懷著振興我國現代數學的理想，婉言謝絕導師的留校建議，決定回國。同時他遵循導師另一項建議——寫一部關于三角級數的專著。當時，他對國際上有關三角級數研究概況已爛熟于心，綜合自己的研究成果和當時國際上傅里葉級數的最新研究進展，用日文撰寫了專著《三角級數論》，交由日本著名的巖波書店出版。該書分2編，第1 編為積分概論，主要介紹三角級數的預備知識，包括點集與積分；第2 編為傅里葉級數，共7 章，其中，第1 章介紹一般三角級數理論，其余6 章介紹傅里葉級數理論。該著作的出版時間比J.D.塔·瑪拉因的《傅里葉級數》早3 年，比波蘭著名數學家A.Zygmund 的名著《三角級數》及S.Kaczmarz 和H.Steinhaus 合著的《正交級數論》第1 版早5 年，僅比L.Tonelli 的《三角級數》晚2 年。可以說，陳建功的《三角級數論》是世界上最早的也是最著名的有關傅里葉級數的專著之一，數十年后該書仍被列為日本最重要的基礎數學參考書之一。l984 年出版的《日本數學100 年史》將《三角級數論》作為日本昭和前期實變函數論領域的一項重要成果。

1.3 學術獎勵

1940 年5 月，民國教育部頒布了《著作發明及美術獎勵規則》。獎勵范圍分三類：一是著作類，二是研究發明類，三是藝術類。獎勵時段為在最近三年內完成的成果[6]。獎勵等級設一等獎、二等獎、三等獎[7]。

經民國教育部學術審議委員會評定，從1941—1947 年，民國政府共頒發六屆學術獎勵。數學學科共有14 位（15 人次）獲得15 項獎勵[8]。其中，一等獎4 項，二等獎3 項，三等獎8 項（包括胡世華獲得的哲學類三等獎1 項）。除此之外，機電專家吳大榕、建筑專家柴方蔭和王仁權分別獲得3 項應用數學成果獲；陸德慧因其在珠算方面的研究獲得1 項鼓勵性質的“獎助”。獲獎領域包括傅里葉級數（5 項）、微分幾何（4 項）、代數與數論（4 項）、應用數學（3 項）、概率論與數理統計（2 項）、珠算（1 項，獲獎助）[7]。其中，有關傅里葉級數的獲獎項目包括

第二屆（1942 年度）：周鴻經以《傅氏級數》（論文）獲二等獎。

第三屆（1943 年度）：陳建功以《傅氏級數之蔡查羅絕對可和性論》（論文）獲一等獎，王福春以《傅氏級數之平均收斂》（論文）、盧慶駿以《傅氏級數之求和論》（論文）獲三等獎。

第六屆（1946 年度）：王福春以《三角級數之收斂理論》（論文）獲一等獎。

在18 項數學類學術獎勵中，傅里葉級數領域獲得5 項，占比27.8%。其中，浙江大學函數論學派獲獎4 項，占所有獎項的22.2%；在數學學科的4 項一等獎中，3 項由浙江大學獲得（另一項由蘇步青于1942 年獲得），其中傅里葉級數領域獲得2 項，占比50%。以上數據以及1.1 節中的2 組數據充分說明了浙江大學函數論學派在我國現代數學發展歷程中的帶頭作用。

1.4 傅里葉級數領域獲得的博士學位

博士學位論文是學者學術研究水平的體現。民國時期，開展傅里葉級數相關研究并獲得數學博士學位的學者共有4 位，全部為浙江大學函數論學派成員。

（1）陳建功，1929 年獲日本東北帝國大學博士學位，導師為藤原松三郎，博士論文題目為《三角級數論》，取得系列研究成果。

（2）徐瑞云，1940 年獲德國慕尼黑明興大學博士學位，導師為世界著名數學家C.Carthéodory，博士論文題目為über die Fourievsche entwicklung der singul?ren funktion bei einer Lebesguesehen ehen zerlegung。

（3）盧慶駿，1948 年獲美國芝加哥大學數學研究院博士學位，導師為世界著名三角級數大師A. Zygmund，博士論文題目為Note on the properties of Fourier cefficients。

（4）程民德，1949 年獲美國普林斯頓大學博士學位，導師為世界著名數學家S.Bochner，博士論文題目為On the uniqueness theorem of multiple trigonometrical series。

2 傅里葉級數在我國的教育概況

我國現代數學教育起步較晚，但發展較快。傅里葉級數在我國的教育主要有3 種形式：大學本科教育、研究生教育、研究討論班教育。

2.1 大學本科教育

從傅里葉級數的本科教學中可以看到，20 世紀30 年代，部分大學已開設級數理論課程，其中包含傅里葉級數理論。例如，北京大學數學系在1931—1935 年各年度課程表[9]中，已有奧斯古德(W. Fogg Osgood，1864—1943)開設的函數各論（乙）課程，并明確標注包含勢函數、三角級數、帶球函數、Bessel函數等。該課程將歐美數學家的3 種原著列為參考書，如美國數學家W. E. Byerly（1849—1935)的《傅里葉級數與球諧函數》(Fouries Series and Spherical Harmonics)[10]，這說明三角級數已經成為當時北京大學數學系本科生課程（屬于選修課程）。

在浙江大學1929、1930 兩年度數學系課程表[11]中，已有級數概論、實函數論等課程，其中，實函數論課程曾以英國數學家E. W. Hobson（1856—l933) 的《實變函數論與傅里葉級數論》(The Theory of Function of a Real Variable and the Theory of Fourier Series)等為主要參考書。由此可見，浙江大學的本科教學內容也包含了豐富的傅里葉級數理論。

2.2 研究生教育

我國傅里葉級數的研究生教育主要集中在浙江大學。1940 年2 月，西遷遵義的浙江大學數學系終于在湄潭等地暫時安定下來，有了一個相對穩定的環境。陳建功與蘇步青協商，創辦浙江大學數學研究所，招收數學研究生。從此，浙江大學數學系跨上了新的臺階。

1940—1946 年，浙江大學在函數論方向共培養了3 位碩士，分別是：

程民德，他是陳建功招收的第一名研究生，研究方向為傅里葉分析，1943 年畢業，碩士論文題目為《三角級數之研究》；

魏德馨，1945 年畢業，碩士論文題目為《線性運算與級數求和法》；

項黼宸，1946 年畢業；碩士論文題目為《傅里葉級數(C.-⊥＜a＜⊥)之求和》。

2.3 研究討論班教育

我國大學授課的研究討論班形式始于浙江大學。自1931 年起，在陳建功與蘇步青的領導下，浙江大學數學系開始舉辦數學討論班[12]，“吸收高年級學生和青年助教參加，并將討論班定名為‘數學研究’”[13]。

陳建功、蘇步青創立的討論班研究性教學方法取得了巨大成功。在函數論討論班中，傅里葉分析是主要討論內容之一。陳建功指導當時的四年級在讀本科生葉彥謙就Paley 與Wiener 關于傅里葉變換的文獻在討論班上做報告[14]，之后，又指導他研讀傅里葉級數方面的論文，希望他開展相關研究工作。從現有資料看，王福春、盧慶駿、徐瑞云、程民德、葉彥謙、馮乃謙、朱良璧、項黼宸、魏德馨等都曾是討論班的學員，而且，都取得了較好的科研成果。

3 我國傅里葉級數學者的學術譜系

關于我國傅里葉分析領域學者的師承關系，按照10 年為一代進行學術譜系劃分。

第一代傅里葉分析學者主要是陳建功，他的導師為日本著名數學家藤原松三郎。陳建功培養了我國第二代傅里葉分析專家王福春。

第二代傅里葉分析學者主要有王福春、周鴻經、周懷衡等。王福春曾是陳建功的學生，后來在日本留學，導師也是藤原松三郎；項黼宸、程民德、魏德馨、葉彥謙等也是陳建功的學生。周鴻經畢業于原東南大學，熊慶來、何魯、段子燮、周家樹等曾是他的老師，后在英國倫敦大學留學，導師為L.S.Bosanquet。周懷衡曾在原東南大學、中央大學學習，熊慶來、何魯、段子燮、周家樹等曾是他的老師，后在英國劍橋大學留學，學習數學。

第三代傅里葉分析學者主要有馮乃謙、盧慶駿、徐瑞云、項黼宸、程民德、魏德馨、朱良璧等。這代學者或在本科或在研究生期間均曾受教于陳建功先生，而項黼宸、程民德、魏德馨等曾受教于王福春先生。盧慶駿的博士生導師為世界著名三角級數大師A. Zygmund；徐瑞云的博士生導師為世界著名數學家C.Carthéodory；程民德的博士生導師為世界著名數學家S.Bochner。S·Bochner 是美國科學院院士，曾任美國數學會副主席，其著作《傅里葉積分講義》引入了被廣泛運用的博赫納積分等研究多重傅里葉級數收斂問題及逼近論問題的重要工具。

我國傅里葉分析學者學術譜系如圖1 所示。其中，虛線框內的為浙江大學函數論學派學者的學術譜系。

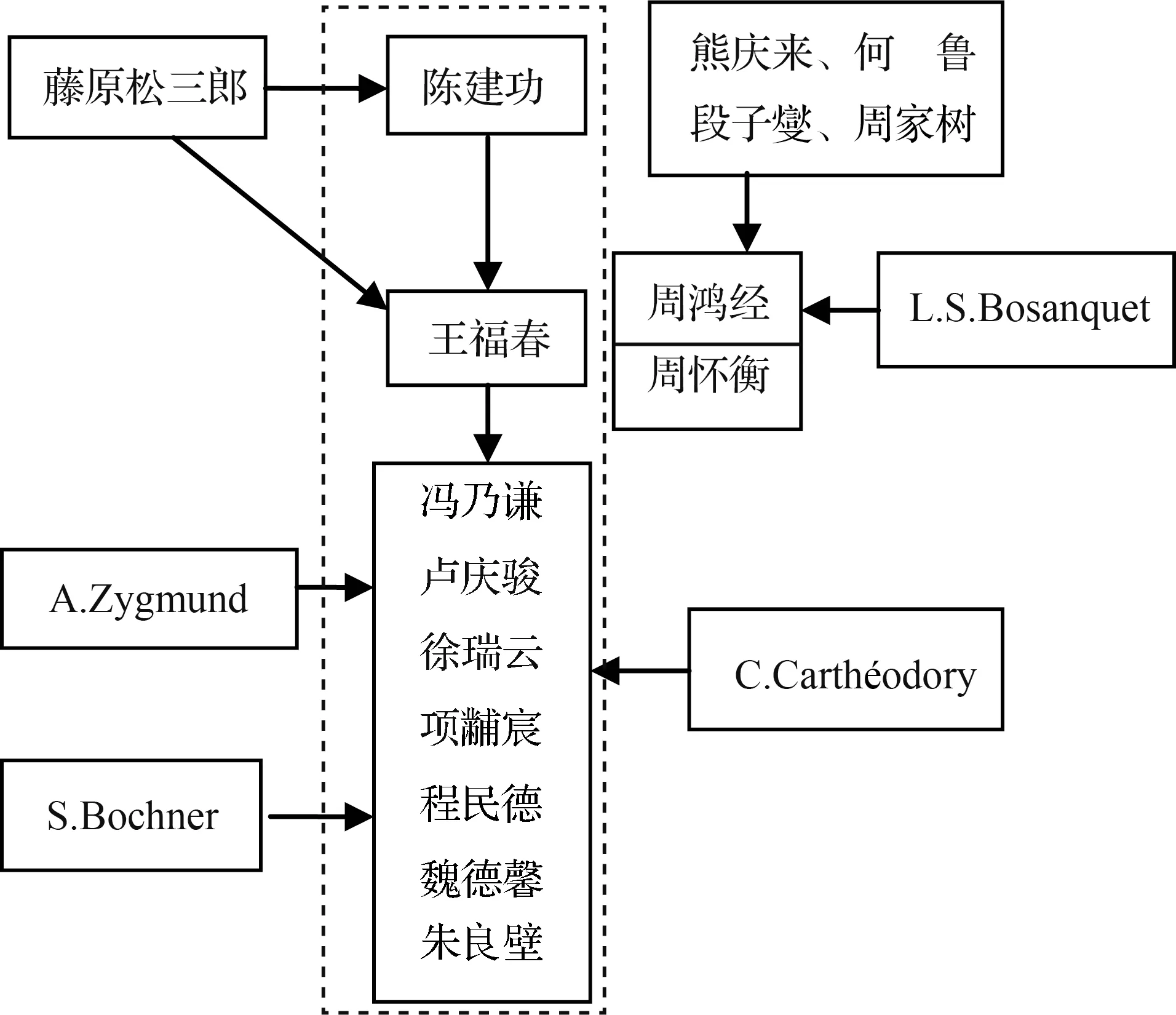
圖1 我國傅里葉級數學者學術譜系Fig.1 The academic pedigree of scholar on Fourier series in China

4 浙江大學函數論學派的主要學術貢獻

4.1 陳建功的主要貢獻［15-16］

陳建功（1893—1971），浙江紹興人。1913 年畢業于浙江兩級師范學堂，同年考取官費留學日本資格，赴日本東京高等工業學校學習染色工藝；1919年回國，受聘于浙江省立甲種工業學校，教授染織工業課程。1920 年，陳建功二次東渡日本，入東北帝國大學數學系學習，次年在日本《東北數學雜志》上發表論文《關于無窮乘積的幾個定理》。據現有資料[3-5]，在此之前，我國學者在國外發表的現代數學論文僅有王季同（1911）、胡明復（1918，博士學位論文）、趙元任（1919，1920）4 篇論文[5]。蘇步青在《陳建功文集》（科學出版社，1981）序言中提到：“（這篇論文）無論是在時間上或是在內容上，都標志了中國現代數學的興起，是具有重要意義的一篇創造性著作。從此以后，特別是從1927 年以后，我國數學家在國內外數學專刊上發表的論文不斷增加。”

1923 年，陳建功畢業，受聘于浙江工業專門學校，教授數學，翌年被聘為國立武昌大學數學系教授。1926 年，他三渡日本，再次進入東北帝國大學數學系攻讀博士學位，師從藤原松三郎，研究三角級數論。這是我國學者系統學習與研究傅里葉級數的始點。

收斂性是傅里葉級數中最為重要的問題。該理論的創始人Fourier 在19 世紀初期就認為，一切周期函數f(x)在滿足一定條件下都是三角級數在點態收斂意義下的和。至1876 年，數學家Du Boise-Reymond 構造了一個周期為2π 的連續函數，在周期區間內除一點外為某三角級數之和，在此例外點上該三角級數不收斂，從而引起了對三角級數收斂性的討論，包括三角級數在一點的收斂性與整體的絕對收斂性，并使得“函數的傅里葉級數是否必收斂于函數本身”成為三角級數研究的中心課題。

關于傅里葉級數整體絕對收斂的判別定理有Bernstain 判 別 法、Zygmund 判 別 法 等。1928 年，陳建功在《日本帝國科學院院刊》第4 卷上發表《論帶有絕對收斂的傅氏級數的函數類》[1]，提出三角級數絕對收斂的刻畫定理：

一個周期為2π 的三角級數絕對收斂的充分必要條件是該三角級數為Young 的連續函數的傅里葉級數。其中，Young 的連續函數是指周期為2π 的函數f(x)，且為2 個平方可積函數的卷積。

同年，英國數學家Hardy 和Littlewood 獲得相同結果，他們的文章發表在《德國數學雜志》第28 卷上。由于《日本帝國科學院院刊》的國際知名度相對較小，因而人們稱這一漂亮結果為“Hardy-Littlewood 定理”，事實上準確的命名應為“Chen-Hardy-Littlewood 定理”。如上所言，這是我國現代數學追趕世界先進水平的第一個標志性成果。

關于傅里葉級數在一點的收斂性的判別方法有多種，如由Dini、Jordan、Dirichlet、Gergen 等數學家建立的方法，但這些判別方法都僅給出了傅里葉級數在一點收斂的充分條件。1930 年，陳建功首先指出傅里葉級數在點x0處收斂的充分必要條件[11]：

對傅里葉級數共軛級數收斂性的判定方法有Misra 判別法。1942 年，陳建功給出了一個新結果[18]，此結果相當于傅里葉級數收斂性的Gergen 判別法，是對Misra 判別法的改進。

1945 年，他進一步討論了傅里葉級數與其共軛級數在點x0處的絕對收斂性：

20 世紀初，自Lebesgue 測度與積分理論問世后，一方面，將Riemann 積分推廣至Lebesgue 積分、Denjoy 積分、Stieltjes 積分，將Cauchy 的連續定義推廣至半連續、平均連續、全連續等；另一方面，Fejer將研究者對傅里葉級數收斂性的討論引導至求和、強性收斂等方面，極大地豐富了傅里葉級數研究的內容和方法。

Cesàro 絕對可和性，即|C,α|可和性，是絕對收斂性的推廣，其中|C,0|可和等價于絕對可收斂。設

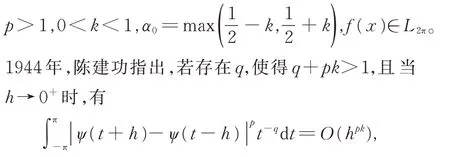
那么，當α＞α0時，f(x)的傅里葉級數在點x0|C,α|可 和；當β＞-k時，f(x) 的 傅 里 葉 級 數 在 點x0|C,β|可和[21]。這一結果推廣了Zygmund 關于傅里葉級數的絕對收斂定理。

1906 年，P. J. L. Fatou（法圖）首先給出了一個傅里葉級數幾乎處處收斂的條件，設

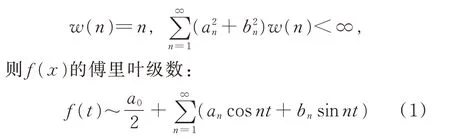
幾乎處處收斂。1909 年，H.Weyl 將條件w(n)=n降為w(n)=；1913 年，E. W. Hobson 又將條件降為w(n)=nε,其中,ε＞0 為 任 意 正 數；同 年M.Plancherel 和G. H. Hard 又分別將條件改進為w(n)=log3n與w(n)=log2n。不久，N. Lsuin 進一步提出猜想（盧津猜想）：w(n)=1，即當式(1)為平方可積函數的傅里葉級數時，其幾乎處處收斂。盧津猜想引起了世界上許多數學家的關注，如A. N.Kolmogoroff 等。圍繞盧津猜想，在長達53 a 的研究中，出現了許多重要成果，如Kolmogoroff 與A.Plessner 進一步將條件w(n)=n降為w(n)=lgn。考慮到傅里葉級數式（1）是由殊特的就范直交函數系{1,sinnx,cosnx},n=1,2,…所組成，人們自然會問，盧津猜想對于一般就范直交函數系{φn(x)}所組成的傅里葉級數是否也成立? H.Rademacher（1922），D. E. Menchoff（1926），S. Bergen 與S.Kaczmarz（1927）分別給出了判別結果，隨后，陳建功于1928 年 指 出，Rademacher,Menchoff，Bergen 與Kaczmant 的判別結果是等價的[22]，為盧津猜想的證明提供了新的思路。1966 年，瑞典數學家L.Carleson 證明了盧津猜想。

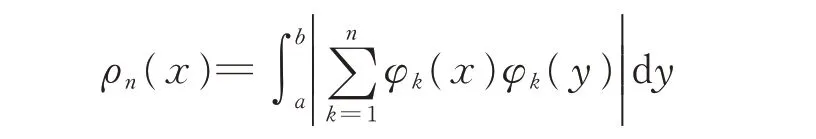
對于區間(a,b) 上的正交函數系{φn(x)}，定義：為 其Lebegue 函 數。1922 年，Rademacher 給 出 了lgn估計：

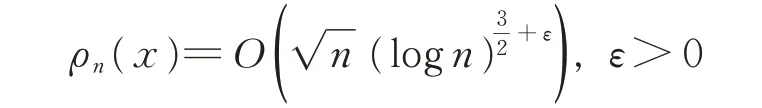
在區間(a,b)幾乎處處成立。

Hilb 認為這一估計是最佳的。1929 年，陳建功對此估計做了改進[23]，得到

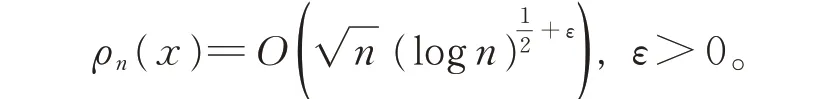
另外，1928—1950 年，陳建功還有6 篇關于單葉函數的論文在國外學術期刊上發表。

4.2 王福春的主要貢獻［24］

王福春（1901—1947），字夢強，江西安福縣人。1922—1927 年在武昌高等師范學校就學，是陳建功先生的學生。1929 年春起，王福春在日本東北帝國大學留學，師從藤原松三郎（亦是陳建功的導師）。研究方向為傅里葉級數與黎曼（Riemann）ζ 函數，研究工作主要集中在傅里葉級數強性求和（strong summability）、絕對求和(absolute summability)、里斯求和(Riesz summability)及求和因子等方面。

王福春的許多工作是基于Hardy 和Littlewood的傅里葉級數研究工作的，并進行了改進與深化。1933 年，王福春在《日本帝國科學院通報》上發表了第1 篇論文[25]，解決了G.H.Hardy 于1931 年提出的2 個問題并推廣了A.Zygmund 用里斯對數平均求傅里葉級數和的定理。

關于傅里葉級數的里斯求和法，王福春討論了(R,ewt,k)的求和法及其在收斂理論上的應用，主要結果如下[26-29]：

（i）若φ(t) 滿 足φ(u)|du=o(t),t→0，則f(x)的傅里葉級數f(t)在t=x處(R,ewt,k)可和；若0 ＜α＜1 對 某 一k＞0 成 立，則f(t)必 在t=x處(R,ewt,h)可和，其中h為任意正數。

（ii）若φ(t)滿足

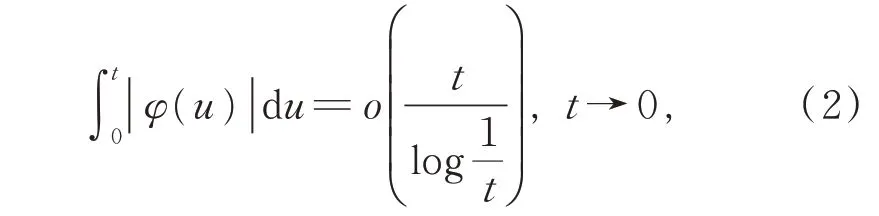
則 對γ＞0，f(x) 的 傅 里 葉 級 數f(t) 在t=x處(R,ewt,γ)可和。

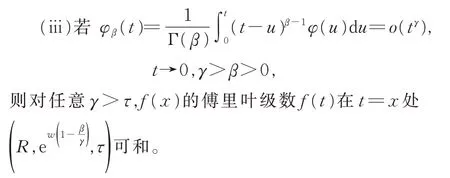
1934 年，Hardy 和Littlewood 在《傅里葉級數收斂的幾個新準則》一書中證明了下述定理[30]：

設f(x)∈L2π是周期為2π 的勒貝格可積函數，若φ(t)滿足式（2），且

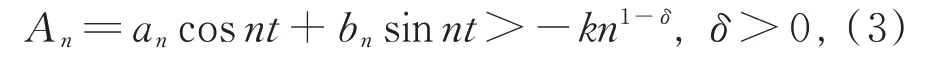
則f(x)的傅里葉級數f(t)在點x處收斂。

進一步，提出問題：定理中式（2）的條件能否減弱為

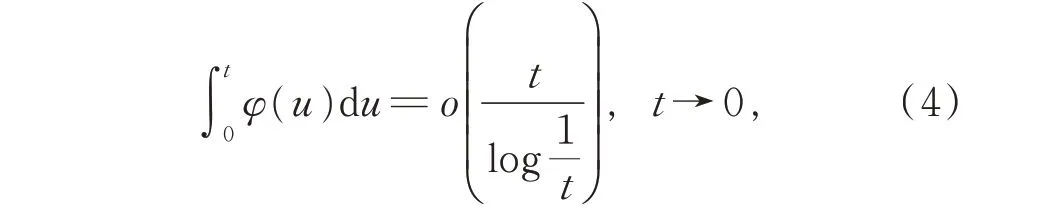
王福春證明了存在連續函數φ(t)，盡管φ(t)滿足式（3）和式（4），但其傅里葉級數在t=0 處是發散的，從而對上述問題做出了否定回答。同時，進一步證明此問題可用(R,e(lgw)2,1+δ)平均法求和，且只需δ＞0。還證明了若將式（2）和式（3）分別改為

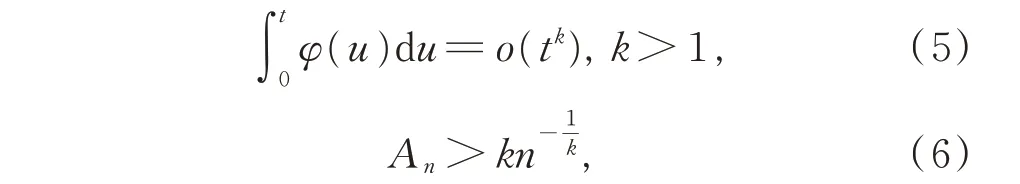
則Hardy-Littlewood 問題成立。同時指出，上述問題還可由下述條件推得：

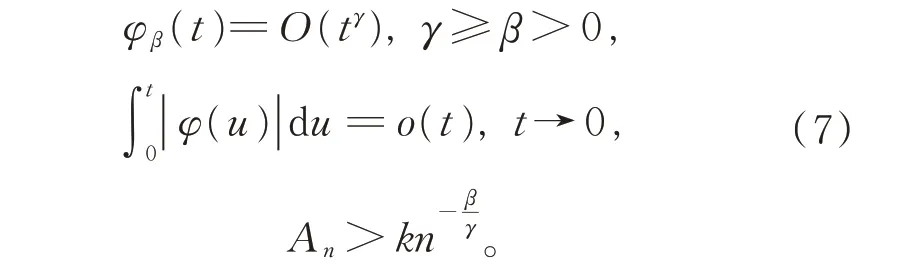
在傅里葉級數強性求和法方面，王福春證明了Hardy 和Littlewood 于1935 年提出 的推測[31]：

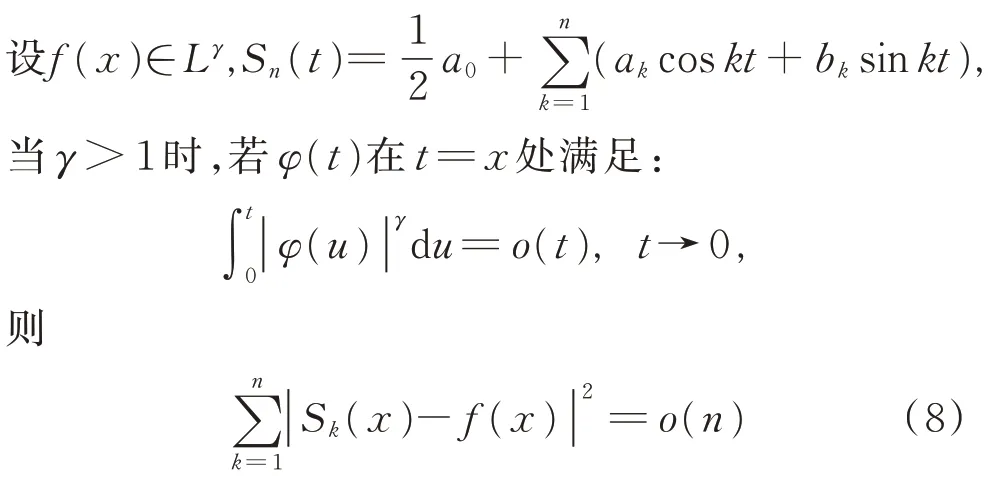
在該點成立。

Hardy 和Littlewood，Carleman 均證明了這一結果，但此結果在γ=1 時不成立。Hardy 和Littlewood 推測：若|f|lg+|f|可積，φ(t)在t=x處滿足

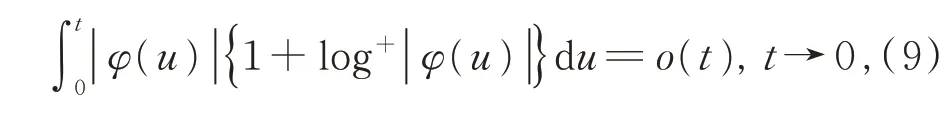
則式（8）成立。

王福春證明了這一推測。進一步，他還證明，若將式（9）改為

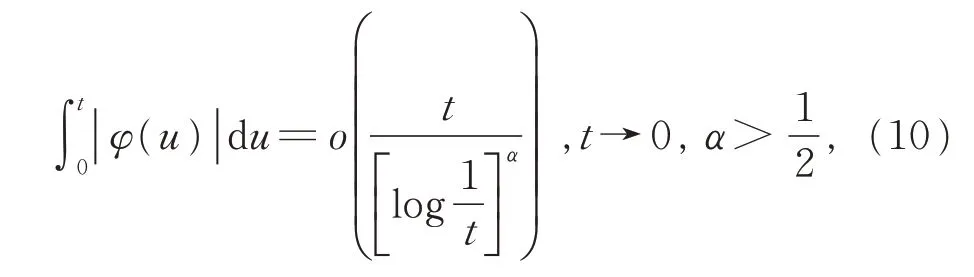
則式（8）也成立[32-34]。

在傅里葉級數絕對求和法方面，王福春得到的主要結果如下[35-36]：

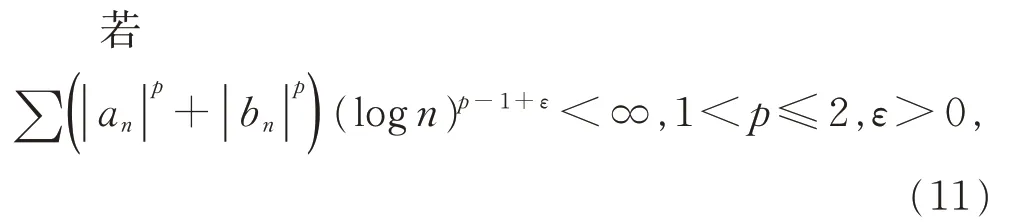
則f(x)的傅里葉級數f(t)幾乎處處|C,α|可和。此時，ε≠0。當ε=0 時，f(t)雖 然 滿 足 式（11），但f(x)的傅里葉級數f(t)在每個t=x處幾乎都不能以|A|平均法求和。

王福春的另一項工作是關于黎曼ζ 函數的研究。民國時期，他在國外學術期刊上發表了6 篇關于黎曼ζ 函數的學術論文。改進了由Littlewood 得到的中值定理，并對黎曼ζ 函數的零點個數進行了估計；改進了由R. Paler 和N. Wiener 得到的中值定理，并獲得一個可比肩普通中值定理的公式。

王福春一直拖病進行黎曼ζ 函數研究，直至去世。

王福春的這些工作得到中外數學界的一致好評。日本巖波書店于1983 年出版的《日本數學100年史》中，介紹了我國留學生陳建功、王福春和蘇步青的工作：“其（王福春）成績使日本治數學者驚異，吾國數學見重于日本，實以陳建功與先生及蘇步青三君為始。”國際著名數學家Hardy 與Littlewood 對王福春亦贊賞有加：“俱于先生之成就，極力贊許”。正因為在傅里葉分析方面的卓越貢獻，王福春2 次獲得民國政府學術獎勵。

由于長期超負荷工作，加之全面抗戰爆發，當時的貴州省湄潭縣物資匱乏，生活困苦、營養缺乏，王福春患上較嚴重的肺病。全面抗戰勝利后，1946 年7 月，浙江大學回遷杭州，王福春因病重只能暫留湄潭，待病情稍有好轉，于1946 年11 月接受中正大學之聘，任新成立的中正大學數學系第一任系主任。在中正大學期間，他一方面主持數學系工作，堅持為學生上課，另一方面仍致力于黎曼ζ 函數研究，終因勞累過度，導致肺病加劇，于1947 年9 月26 日病逝于南昌，享年46 歲。

4.3 盧慶駿的主要貢獻

盧慶駿(1913—1995)，江蘇鎮江人。1936 年8 月畢業于浙江大學數學系，后留校任教。1946 年9 月被選派至美國芝加哥大學數學研究院學習，師從國際著名三角級數大師A.Zygmund，1948 年獲博士學位，1949 年回國并被聘為浙江大學數學系教授，兼任數學系主任。

從1941 年至1950 年，在陳建功先生的指導下，盧慶駿主要從事傅里葉級數分析研究，先后發表11篇有關傅里葉級數的研究論文。其中最有名的工作是與王福春、程民德等一起共同解決了著名數學家G.H.Hardy，J.E.Littewood 和Z.Zalewaser 等提出的一個懸而未決的問題：

設{Sn(k)}為可積函數f(x)的傅里葉級數的部分和數列，{Sn(k(x))}是否幾乎處處可用α＞0 階Cesáro 求和？

王福春解決了k=2 的情形，程民德解決了k=2和3 的情形，盧慶駿利用Van der Corput 關于三角和的絕對值估計結果，完全解決了Z.Zalewaser 問 題[37]。

此后，盧慶駿在缺項傅里葉級數、傅里葉級數強性求和等方面獲得了一系列結果，并在冪級數與傅里葉級數的絕對求和性方面得到了較深入的結果。1943 年，盧慶駿以《傅氏級數之求和論》（論文）獲民國政府學術獎勵三等獎。

4.4 徐瑞云的主要貢獻［38］

徐瑞云（1915—1969），浙江慈溪人，是我國第一位數學女博士。1936 年，她以優異的成績畢業于浙江大學數學系，后留校任教。1937 年10 月，進入德國慕尼黑明興大學，師從著名數學家C.Carathéodory，研究三角級數論。

1940 年，徐瑞云獲得博士學位，學位論文題目為《關于勒貝格分解中奇異函數的傅里葉展開》[39]，該文主要研究有界變差函數傅里葉級數的特征。1941 年，她返回浙江大學，被聘為副教授，繼續研究有界變差函數傅里葉級數的特征，得到以下重要結果[40]：

設f(θ)是區間0 ≤θ≤2π 中的有界變差函數，其 變 差f(2π-0)-f(+0)=πσ( ＞0)，設 其 傅 里葉級數為

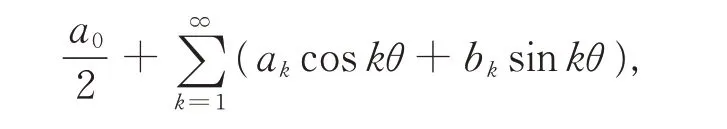
此時有勒貝格分解：

徐瑞云指出，對滿足上述條件的所有函數f(θ)，在2n維空間中的點：

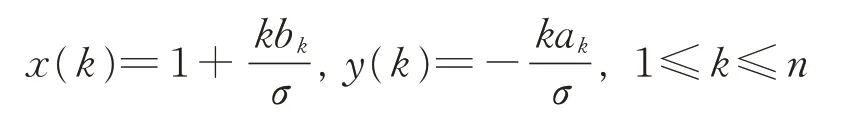
的變化范圍是一個n階Carathéodory 區域；進一步，如果前2n個傅里葉級數的系數ak,bk(1≤k≤n)保持不變，則在由此類函數構成的函數集中，S有正的最小值S*n，且S*n還可用此2n個傅里葉級數的系數表示。

4.5 程民德的主要貢獻［41］

程民德（1917—1998），1935 年考入浙江大學電機系，后轉入數學系學習；1940—1942 年，在浙江大學數學研究所攻讀碩士學位，師從陳建功先生，研究方向為傅里葉分析理論；1943—1945 年，任浙江大學數學系講師；1946—1947 年，任北京大學數學系講師；1947 年，進入美國普林斯頓大學數學系，在著名數學家S.Bochner 教授指導下，進行多元調和分析研究，1949 年獲得博士學位；后在著名數學家E.Artin 與C.Chevalley 指導下做博士后研究，1950 年1月回國。

程民德的早期工作是研究一元傅里葉級數各種求和法以及求和因子等，共發表學術論文21 篇。如前所述，他的第1 篇論文是與王福春、盧慶駿一起解決 了Hardy，Littlewood 和Z.Zalewaser 等 提 出 的 問題[42]。第2 篇論文得到了三角級數在整個區間上收斂的充分必要條件[43]。此后一段時間，他的主要工作集中在傅里葉級數的Cesáro 可求和性、傅里葉級數的可求和性因子、Bochner-Riese 平均的Gibbs 現象等方面。在文獻[44]中，他證明了以下結果：

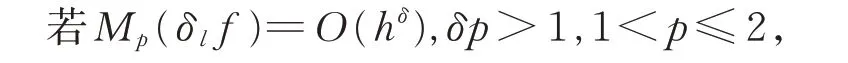
則[φ(t)]1在(0,π)是有界變差的，且[φ(t)]1的傅里葉級數絕對收斂。

在文獻[45]中，他得到了傅里葉級數在點x處的可求和性條件。

程民德的另一主要貢獻是在調和分析方面。調和分析也稱傅里葉分析，來源于傅里葉級數，形成于18 世紀。但由于多種原因，20 世紀40 年代前，多元調和分析一直未能取得實質性突破。程民德在S.Bochner 指導下，將研究方向從一元轉向多元，很快在多重三角級數唯一性上取得了成果[46]。調和函數是滿足拉普拉斯方程Δu=0 的二次連續可微函數，而m重調和函數是滿足方程Δm u=0 的2m次連續可微函數。但當函數u僅有較少的光滑性時，如僅知u有2m-2 次連續可微時，如何刻畫u的m重調和 性？1916 年，W.J.E.Blaschke 解 決 了m=1 的 情形；20 世紀30 年代，D.Nicolesco 對 一般的m做了類似的刻畫。程民德證明了：如果二重（或多重）三角級數的圓形和按|C,1|可求和到零，則其系數皆為零。為證明多重三角級數的唯一性定理，他將研究領域拓展至多重調和級數，并發現D. Nicolesco 對一般的m做的有關函數u的m重調和性，給出的僅為必要而非充分條件。為此，他引進了廣義多重拉普拉斯運算概念（記為?m），并且在函數u是2m-2次連續可微條件下證明了Δm u=0 的充分必要條件是?m u=0。這一結果堪稱經典。

限于篇幅，有關項黼宸、朱良璧、魏德馨等的工作不再贅述。

5 總 結

陳建功是我國傅里葉級數研究的開創者、領導者。浙江大學函數論學派是傅里葉級數在我國的主要研究、教育、傳播、發展基地。陳建功培養了王福春、盧慶駿、徐瑞云、項黼宸、程民德、魏德馨等我國第二代、第三代傅里葉級數學者。王福春、周鴻經等我國第二代傅里葉級數學者，對于推動傅里葉級數在我國的傳播、研究和發展起了積極作用。徐瑞云、程民德等是我國第三代傅里葉級數學者，對于傅里葉級數在我國的進一步發展起了承前啟后的作用。項黼宸、程民德、魏德馨是1949 年前我國培養的傅里葉級數方向的碩士。傅里葉級數研究是我國現代數學研究的先驅與領頭羊，對于推動現代數學在我國的傳播、發展起了帶頭和引領作用。