基于超網絡和投影降維的高維數據流在線分類算法

茹 蓓

(新鄉學院計算機與信息工程學院 河南 新鄉 453003)

0 引 言

近年來出現了許多數據流的實時分類應用，例如：金融市場通過對證券股指、期貨數據進行實時分類和預測，能夠快速察覺市場行情的變化，有助于提高投資收益和降低風險[1]；社交媒體用戶每天需要發布大量的圖像數據流，通過對圖像進行實時分類和預測，能夠快速檢測出非法圖像[2]。對數據流的實時分類和預測存在巨大的應用價值[3]，而圖像、文檔等高維數據是數據流的一個重要組成部分，其高維特性嚴重影響了分類器的計算效率和分類性能，成為實時數據流分類的一個難點[4]。

增量學習思想是當前數據流實時分類的一個重要手段，文獻[5]提出了噪聲消除的增量學習分類器，使用互信息近鄰來檢測噪聲樣本，通過增量學習檢測數據流的類標簽。文獻[6]提出基于樣本不確定性選擇策略的增量數據流分類模型，從相鄰訓練集中按照樣本不確定性值選出“富信息”樣本代表新概念樣本集。增量學習主要通過一些評價指標檢測出某些判別能力強的新到達樣本，然后結合這些樣本對分類器進行更新，此類方法主要以上一個時間窗口的模型為基礎，導致變化劇烈窗口的訓練集存在明顯的偏差，難以實現理想的分類準確率。文獻[7]將回歸系統應用于時變環境，實現了回歸神經網絡，該方法通過回歸模型主動學習神經網絡的模型參數，實現了較為理想的性能，雖然采用了簡單的神經網絡結構，但該模型的回歸模型依然存在訓練時間長的問題。

基于神經網絡的數據流分類器一般通過增量學習機制動態地更新神經網絡的參數，采用多層神經網絡處理高維數據流才能獲得更好的效果，但多層神經網絡的參數量較多，實時學習的難度較大[8]。本文從一個新的角度出發，對高維數據流進行分析和分類處理。采用超網絡建模高維數據流的數據空間，利用基于高斯核的投影技術將高維數據投影到低維空間。利用貝葉斯模型的先驗分布、后驗分布和似然信息擬合數據流的動態特性，設計了貝葉斯模型的實時更新方法，實現了對高維數據流的實時分類處理。

1 高階模型的超網絡

超圖[9]是離散數學中有限集合的子系統結構，超圖的邊為高階邊，稱為超邊，超邊連接兩個以上的頂點。將超圖表示為G=(V,E)，其中V和E分別是頂點集和超邊集。一條超邊是V的一個子集，超邊的權重滿足w(e)≥0。頂點的度和超邊的度d(v)和δ(e)分別定義為：

(1)

δ(e)=|e|

(2)

式中：|e|為邊e的基數，將度等于k的超邊簡稱為k-超邊。超邊的度值越高，則該超邊的模式判別能力越強。如果一個超圖的超邊均為k-超邊，則稱其為k-均勻超圖，所以2-均勻超圖即為傳統意義的圖，3-均勻超圖即為三元組的集合，以此類推。

超網絡[10]是超圖結構的高階表示，超網絡的頂點定義為一個變量及其取值，超邊定義為頂點間的高階連接，超邊的權重表示連接的強度。超網絡是大量超邊的集合，可表征高維數據特征之間的高階關系。

將超網絡定義為一個三元組形式H=(V,E,W)，其中W表示超邊的權重集。超邊是兩個以上頂點的集合，表示為：

ei={vi1,vi2,vi3,…,vi|ei|,yi}

(3)

式中：yi表示第i個超邊ei的類標簽。超邊的權重反映了超邊對于類標簽的判別能力，所以可將超邊考慮為一個弱學習機，學習分類器所需的特征子集。圖1為一個超網絡及超圖結構的示意圖。

(a)超網絡實例

給定一個數據點集x(n)、一個類標簽集Y和一個超網絡H，選擇x(n)超邊加權調和值最大的標簽，將該極大值標簽作為x(n)的類標簽。超網絡模型的分類步驟如下：

步驟1計算超邊集E中所有y∈Y超邊的權重之和：

(4)

式中：w(ei)表示ei的權重。

步驟2選擇總權重最大的標簽作為x(n)的標簽：

(5)

定義兩個指示函數f(x(n),ei)和φ(y(n),yi)，如果ei匹配x(n)，則f(x(n),ei)=1；如果y(n)=yi，則φ(y(n),yi)=1，即：

(6)

(7)

式中：c(x(n),ei)表示匹配的數量；θ為匹配的閾值，用于增強對噪聲數據的魯棒性。

超網絡的模型結構對分類算法的性能具有極大的影響，學習程序的目標是尋找最優的超邊集，即從一個特征集選出特征子集。該問題主要分為3個子問題：(1)選擇構建超邊的變量子集;(2)確定超邊的度;(3)確定模型的超邊數量。子問題(1)和(2)影響分類器的分類性能，子問題(2)和(3)影響模型的計算復雜度。如果特征為二進制值，那么特征集的規模為22|x|，|x|為數據的維度，超網絡模型對于高維數據的計算復雜度較高，因此為超網絡設計一個高效的模型學習方法，即基于貝葉斯模型的超網絡更新機制。

2 基于貝葉斯模型更新超網絡

圖2為超網絡數據流分類算法的結構框圖，使用貝葉斯更新方法學習超網絡的結構，學習的內容包括生成超邊、更新超邊權重和評估超網絡模型。首先，從訓練數據集提取超邊，構建初始化超網絡，將超邊和訓練數據匹配計算超邊的權重。然后，將訓練集分類估算模型的適應度，將低權重超邊替換為新生成的超邊，動態地修改模型。

圖2 超網絡高維分類算法的結構框圖

2.1 貝葉斯模型的學習方法

引入貝葉斯模型學習超網絡，貝葉斯模型假設后驗分布和先驗分布分別為當前種群(當前超網絡)和上一代種群(上一代超網絡)。模型的適應度定義為后驗概率，適應度同時反映了數據的判別能力和模型的復雜度。

(8)

式中:p(Y|X,Ht)和p(Ht|X)分別為似然信息和先驗分布；p(Y|X)是一個正則常量。后驗分布關于似然信息和先驗分布的乘積成正比例關系：

p(Ht|X,Y)∝p(Y|X,Ht)p(Ht|X)

(9)

定義Ht的適應度函數Ft為后驗分布的對數，目標函數變為最大化式(10)：

Ft=logp(Y|X,Ht)+logp(Ht|X)

(10)

即

(11)

2.2 采用貝葉斯模型學習超網絡結構

計算超網絡的適應度需要定義模型的先驗信息和似然信息，將經驗先驗分布p(Ht|X)定義為目標問題的先驗知識。超網絡的先驗信息包括兩點：(1)變量和類標簽之間的相似性矩陣，采用基于投影的相似性矩陣選擇數據，產生初始化超邊；(2)縮小模型的規模，從上一次的后驗分布p(Ht-1|Y,X)計算當前迭代的經驗先驗分布：

p(Ht|X)∝p(Ht-1|Y,X)

(12)

(13)

式中：Et為Ht的超邊集；P(e)表示超邊e的產生概率；PI(xi)表示選擇變量xi的概率；PI(xi)關于xi和類標簽之間的相似性成正比例關系。僅需要對每個新到達時間窗口計算一次PI(xi)，在更新過程中無需改變該概率值。通過上述方法可確定超網絡模型的3個主要參數：超邊包含的變量、超邊的度和超邊數量。

似然定義為從Ht正確分類Y的條件概率，X表示了Ht的判別能力。統計模型對訓練數據正確匹配和錯誤匹配的數量，再計算每個超邊的加權調和值，通過評估超邊的判別能力估算似然信息。如果超邊和一個數據實例的標簽匹配，則認為該超邊正確匹配，否則匹配失敗。總似然計算為各個數據實例似然的乘積：

(14)

將經驗似然定義為：

p(y(n)|x(n),Ht)≡

(15)

式中:w(ei)為第i個超邊的權重；Et為Ht的超邊集合。如果經驗似然小于0，則將其設為一個小的正數來防止出現負似然的情況。可獲得：

(16)

在訓練程序中，如果正確匹配一條超邊，那么fi(n)·φi(n)和fi(n)(1-φi(n))分別等于1和0；如果錯誤匹配，則分別為0和1；如果匹配失敗，則兩個值都為0。

超邊的權重是關于正確匹配情況和錯誤匹配情況的函數：

(17)

式中：α是小于1的常量，用來增加正確預測的概率；β是一個小的正常量。因為度小的超邊匹配率更高，所以如果兩個超邊的度接近，則選擇度小的超邊，β不僅減少了模型的復雜度，而且增加了模型的泛化效果。如果w(e)小于0，則設為0，防止出現負權重。

結合式(13)的經驗先驗和式(16)估算的似然，將超網絡的適應度修改為：

Ft=logp(Y|X,Ht)+logp(Ht|X)≈

(18)

式中:λ和ζ均為正常量，λ負責調節模型的大小，ζ負責調節先驗信息的變量選擇能力。

綜上所述，提高適應度的措施有三點：(1)每次迭代保留權值高的超邊；(2)選擇PI(x)概率大的變量生成超邊；(3)在保持模型判別能力的情況下，盡量減少超邊的數量。超網絡更新的結束條件是在連續幾次迭代后，Ft均不大于Fmax，或者達到最大迭代次數Imax。

2.3 基于高斯核投影的相似性度量

直接度量高維數據的相似性不僅準確率低而且計算復雜度也較高，因此本文采用高斯核的投影技術計算高維數據之間的相似性矩陣。設S(xi,xj)為數據xi和xj間的相似性，其投影矩陣定義為[P]i,j=S(fDR(xi),fDR(xj))，其中：i和j是矩陣的行和列，fDR為投影函數。本文的目標是將高維空間的數據點投影到低維空間，設目標相似性矩陣是一個方陣T，則需要優化以下的目標函數：

(19)

表示矩陣M的l1范數。如果每對數據點超過了目標相似性，此時的目標函數則是最小值。

(20)

設c(x)為低維空間的相似性度量(例如：歐氏距離)，可將目標矩陣T中的元素定義為：

(21)

式中:σc為縮放因子。

采用核方法實現投影處理，設Φ=φ(X)為Hilbert高維空間[12]的數據矩陣，φ(X)為高維空間的投影函數，然后學習從高維空間到低維空間的線性映射。將矩陣W重新定義為：

W=φ(X)TA=ΦTA

(22)

式中:A∈Rn×m為系數矩陣。將投影定義為數據點的線性組合，可獲得以下的投影方法：

YT=WTΦT=ATΦΦT=ATK

(23)

式中:K=ΦΦT∈Rn×n是數據的核矩陣，表示Hilbert空間數據點的內積，即Kij=φ(xi)Tφ(xj)T。

核方法學習系數矩陣A，采用梯度下降法優化目標：

(24)

(25)

2.4 學習超網絡的方法設計

貝葉斯更新模型包括：生成超邊、選擇超邊和更新超邊。生成超邊需要確定兩個屬性：(1)超邊的數據變量；(2)超邊的度。圖3為生成超邊的示意圖。

圖3 生成超邊的示意圖

根據變量之間的投影相似性矩陣選擇相似的變量，相似的變量組成一條超邊。式(13)的PI(xi)計算為：

(26)

式中:I(xi;y)表示變量xi和類y間的相似性(基于投影計算高維數據的相似性);η為一個非負常量，該常量防止相似性過小。將η和式(18)的ζ設為反比例關系。

根據Ht-1超邊度的概率決定Ht超邊的度：

(27)

算法1生成超邊的程序

輸入：數據集S={S1,S2,…,SN}。

輸出：超邊e。

/*初始化程序*/

n←從|D|隨機選擇數據樣本；

d←D[n]；

K←通過式(27)計算邊的度；

For eachkfrom 1 toKdo

idx←式(26)選擇變量;

val←d數據的xidx;

v←(idx,val)；

e←e∪{y(n)};

end for

e←e∪{y(n)}；

w(e)←0；

在迭代過程中刪除低權重的超邊，增加新的超邊，但可能存在相似的冗余超邊，導致計算復雜度升高。因此式(18)的適應度有效維護了超網絡的大小，如果Ft大于Ft-1，則縮小超網絡，否則擴大超網絡。

設Rt和Gt分別表示在第t次迭代刪除的超邊數量和新產生的超邊數量。將Rt定義為一個關于t的函數，Gt定義為一個關于Rt的函數，Rt和Gt分別定義為：

(28)

Gt=γt·Rt

(29)

式中:Rmax和Rmin分別表示Rt值的上界和下界；κ為一個常量，控制Rmax到Rmin的變化速率;γt為泛化模型的比例系數，定義為：

(30)

式中:ΔFt=Ft-Ft-1；τ控制種群縮小的速度，如果τ=0，那么種群規模保持不變。

圖4為基于貝葉斯的超邊更新算法流程圖，根據數據集的先驗知識生成初始化超網絡，將超標權重和特征的判別能力作為貝葉斯的似然信息，將超網絡的復雜度和適應度作為貝葉斯的后驗分布，貝葉斯迭代地學習最優的超網絡結構。基于貝葉斯的超邊更新算法偽代碼如算法2所示。

圖4 基于貝葉斯的超邊更新算法流程示意圖

算法2基于貝葉斯的超邊更新程序

輸入：訓練集D，所有變量的相似性矩陣SM，第t次迭代刪除的超邊數量Rt，第t次迭代新生成的超邊數量Gt，第t次迭代的超邊集Et，第t次迭代的超網絡Ht，最大迭代次數Imax，H0的初始化超邊數量Hinit。

1.E0←NULL,H0←NULL;

//初始化

2.計算SM(D,SM)；

//式(26)

3.for eachifrom 1 toHinitdo

//建立初始化模型

4.ei←生成超邊；

//式(27)

5.wi←評價權重；

//式(17)

6.E0←E0∪ei；

7.end for

8.利用式(18)評估當前模型的適應度；

9.E1←利用式(22)刪除低權重超邊；

10.for eachtfrom 1 toTdo

//超邊迭代更新模塊

11. forifrom 1 toGtdo

12.ei←生成超邊；

//式(27)

13.wi←評價權重；

//式(17)

14.E0←E0∪ei；

15. end for

16. 以式(18)評估當前模型的適應度；

17. if未滿足結束條件then

18.H←H×Ht；

19. eles

20. break;

21. end if

22.Et+1←刪除低權重超邊；

//式(28)

23.數據流分類

3 實 驗

3.1 實驗環境和實驗方法

實驗環境為PC機，處理器為Intel Core i5-4570，內存為16 GB，操作系統為Ubuntu 14.04 LTS，軟件的編譯環境為MATLAB R2017a。

將數據集排列成序列形式，每個到達數據首先用來測試在線分類器的分類性能，再用來更新分類器的模型。每組實驗將每個數據集做10次置亂處理，置亂數據集作為輸入數據，獨立完成10次實驗，統計10次實驗的平均誤差率和標準偏差值。

3.2 實驗數據集

采用10個UCI高維數據集作為實驗的benchmark數據集，表1為benchmark數據集的基本屬性。數據集排列成序列形式來模擬數據流。

表1 10個高維benchmark數據集的基本屬性

3.3 對比實驗方法

選擇4個近期的數據流在線分類器作為對比方法：

(1)基于演化的在線貝葉斯分類器[13]，簡稱為OnlineBayes，該方法與本算法同屬于采用貝葉斯分類器的在線分類方案。

(2)基于元神經元的脈沖神經網絡分類器[14]，簡稱為OnlineSpikingNeural，該方法是基于神經網絡的在線分類器。

(3)基于混合分類回歸樹和模糊自適應諧振網絡的在線分類器[15]，簡稱為FAM-CART，該方法較為新穎，且性能較為突出。

(4)在線的廣義分類器[16]，簡稱為onlineuniversal，該分類器支持多種類型的數據流。

本文算法簡稱為HypernetworksBayes。

3.4 分類器性能實驗結果

1)高維數據流的分類錯誤率。首先評估5個分類器對于10個高維數據流的分類準確率，采用分類誤差率作為度量指標，圖5為總體的統計結果。可以看出，HypernetworksBayes對于Biodeg和Spambase 2個數據集的分類錯誤率高于FAM-CART，HypernetworksBayes對于Ring數據集的分類錯誤率也高于onlineuniversal算法，但結果也較為接近。對于數據流的二分類問題，本文算法與其他優秀的分類器較為接近，但對于其他高維數據的多分類問題，本文算法的優勢則較為明顯。FAM-CART對于10個高維數據流均表現出較低的分類錯誤率，FAM-CART采用分類回歸樹和模糊自適應諧振網絡2項技術，模糊自適應諧振網絡具有較強的自適應和自調節能力，而分類回歸樹對于連續性數據流具有較強的處理能力，因此實現了較好的效果。比較OnlineBayes和HypernetworksBayes可見，HypernetworksBayes的分類錯誤率遠低于OnlineBayes分類器，即本文的超圖理論和基于高斯核投影的降維處理有效地提高了分類器的性能。總體而言，本文算法的分類錯誤率低于其他4種算法。

圖5 5個分類器對高維數據流的分類錯誤率的比較

2)分類器統計檢驗。通過Friedman檢驗[17]測試分類器對于10個數據集分類結果的差異，Friedman檢驗的顯著性設為0.05。Friedman檢驗獲得的排名如圖6所示。本文算法排名第一，且遠高于第二名，再次驗證了HypernetworksBayes分類器的性能優勢。

圖6 分類器的Friedman檢驗結果

Friedman檢驗能夠比較多個分類器之間的性能，而驗后比較檢驗(post-hoc test)能夠詳細比較多個分類器和單一分類器的性能。通過驗后比較檢驗進一步分析分類器的性能，根據文獻[18-19]的討論，Hommel檢驗適合評估數據流的在線分類器的性能，所以采用hommel post-hoc對分類器進行驗后比較檢驗分析，結果如表2所示。觀察表中各個分類器的p-value值，HypernetworksBayes明顯優于其他4個分類器，而對比方案中OnlineSpikingNeural和FAM-CART的性能也較為理想。

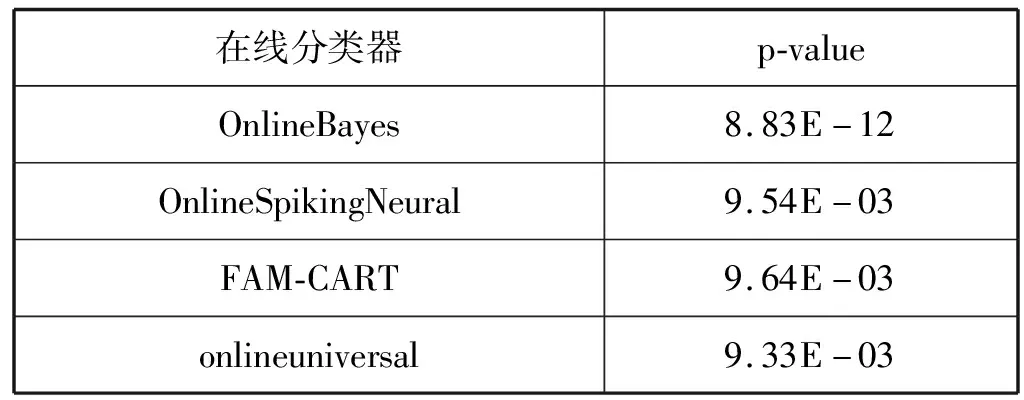
表2 分類器的hommel post-hoc檢驗

3.5 分類器的時間效率

時間效率是數據流在線分類器的一個重要性能指標，直接決定了分類器的應用價值。為了評估在線分類器的時間效率，統計了5個分類器每組實驗分類程序的平均時間，結果如圖7所示。可以看出，OnlineSpikingNeural和FAM-CART的處理時間遠高于其他3個算法，這2個算法均為基于神經網絡的分類器，在訓練神經網絡的過程中難以同時在網絡性能和時間效率兩方面均取得理想的平衡。受益于貝葉斯模型的高計算效率，OnlineBayes的時間效率最高。Onlineuniversal分類器不包含復雜的計算和模型，也實現了極高的時間效率。HypernetworksBayes的時間效率略低于OnlineBayes分類器和Onlineuniversal分類器，但是也足以滿足處理實時數據流的時間需求。

圖7 5個在線分類器的平均處理時間的比較

3.6 噪聲數據流的分類實驗結果

在實際的數據流應用中，數據流均伴隨著不可忽略的噪聲數據，因此測試了在線分類器對于噪聲數據流的性能。隨機選擇一個錯誤類標簽，替換訓練數據集的正確標簽，訓練集的噪聲數據比例分別設為10%、20%和30%。訓練集為噪聲數據集，測試數據集為無噪聲數據集，使用10折交叉驗證完成每組數據集的實驗，計算10次獨立實驗分類錯誤率的平均值。因為Optdigits和Penbased兩個高維數據集的分類錯誤率較低，所以重點測試并統計了噪聲數據對于Optdigits和Penbased兩個高維數據集的影響。

圖8為Optdigits和Penbased兩個高維數據集的實驗結果。可以看出，隨著噪聲比例的增加，本文算法分類錯誤率略有升高，但上升幅度較小。OnlineBayes和onlineuniversal兩個分類器受噪聲的影響較大，幾乎不具備噪聲魯棒性，因此可得結論：本文的改進措施有效地增強了分類器的魯棒性。

(a)Optdigits數據集

4 結 語

本文設計了基于超網絡和投影降維的高維數據流在線分類算法，利用貝葉斯模型的先驗分布、后驗分布和似然信息擬合數據流的動態特性，設計了貝葉斯模型的實時更新方法，實現了對高維數據流的實時分類處理。本文算法利用高斯核將高維空間的數據點投影到低維空間，實現了較高的高維數據流分類準確率，并且對于噪聲也具有較好的魯棒性。

本文模型依然存在一些限制：無法處理不平衡數據流，而不平衡數據流也是實時數據流領域的一個細分領域；僅支持數據維度權重相等的情況。未來將嘗試引入分級的超網絡模型，解決特征維度權重不相等的問題，從而可將本方案運用到推薦系統等多屬性度量的應用中。