PSO-SVR-RSM在加氫反應器氣液分配器結構優(yōu)化中的應用

李立毅，張 瑋，延會波，翟 劍，韓念琛

(太原理工大學化學化工學院，太原 030024)

滴流床反應器被廣泛應用于加氫精制和加氫裂化等處理過程，氣液分配器是滴流床反應器中的重要內構件，其功能是將原料均勻噴灑到催化劑床層表面，從而使催化劑充分發(fā)揮作用，所以氣液分配器直接影響反應器內物流混合分配效果及催化劑利用率[1]。目前，對氣液分配器的研究主要采用計算流體力學(CFD)模擬的方法。王少兵等[2]使用CFD模擬輔助開發(fā)了一種頂部具有旋流葉片結構的泡帽型氣液分配器；王振元[3]利用CFD開發(fā)了一種能夠使氣液分布均勻且具有良好抗塔板傾斜性能的氣液分流式分配器。侯亞飛等[4]利用CFD模擬對BL型分配器進行了結構優(yōu)化。

雖然CFD是一種功能強大的工具，可以對氣液分配器內的流體流動情況和液體分配性能進行準確的模擬研究，但是要以時間成本為代價來滿足要求。在對氣液分配器結構參數進行優(yōu)化時，要進行多次分析，時間成本會不斷增長，因此需要探索一種快速可靠的代理模型來代替CFD模擬，從而降低計算成本。例如機器學習工具，只需要根據給定的設計變量值得到一套基于CFD的解后，就可以訓練機器學習模型來獲得其他設計變量值的解。在這項研究中，由Vapnik等[5]首先引入的支持向量回歸方法(SVR)被實現為機器學習模型，在過去的二十年中，許多研究人員已將這種方法用于各種工程問題的計算[6-8]。

本研究以文獻[9]中的氣液分配器(結構如圖1所示，其中：D為喉管直徑；H為喉管位置高度；L為喉管長度)為研究對象，結合文獻中收集的144組CFD模擬試驗數據，建立一種基于粒子群優(yōu)化算法(PSO)-SVR的滴流床氣液分配器液體分布的快速預測模型，然后以PSO-SVR代理模型為數據源，采用響應面法(RSM)獲得該分布器對應于最小分布不均勻度時的最佳結構，最后通過CFD模擬對該方法進行驗證。

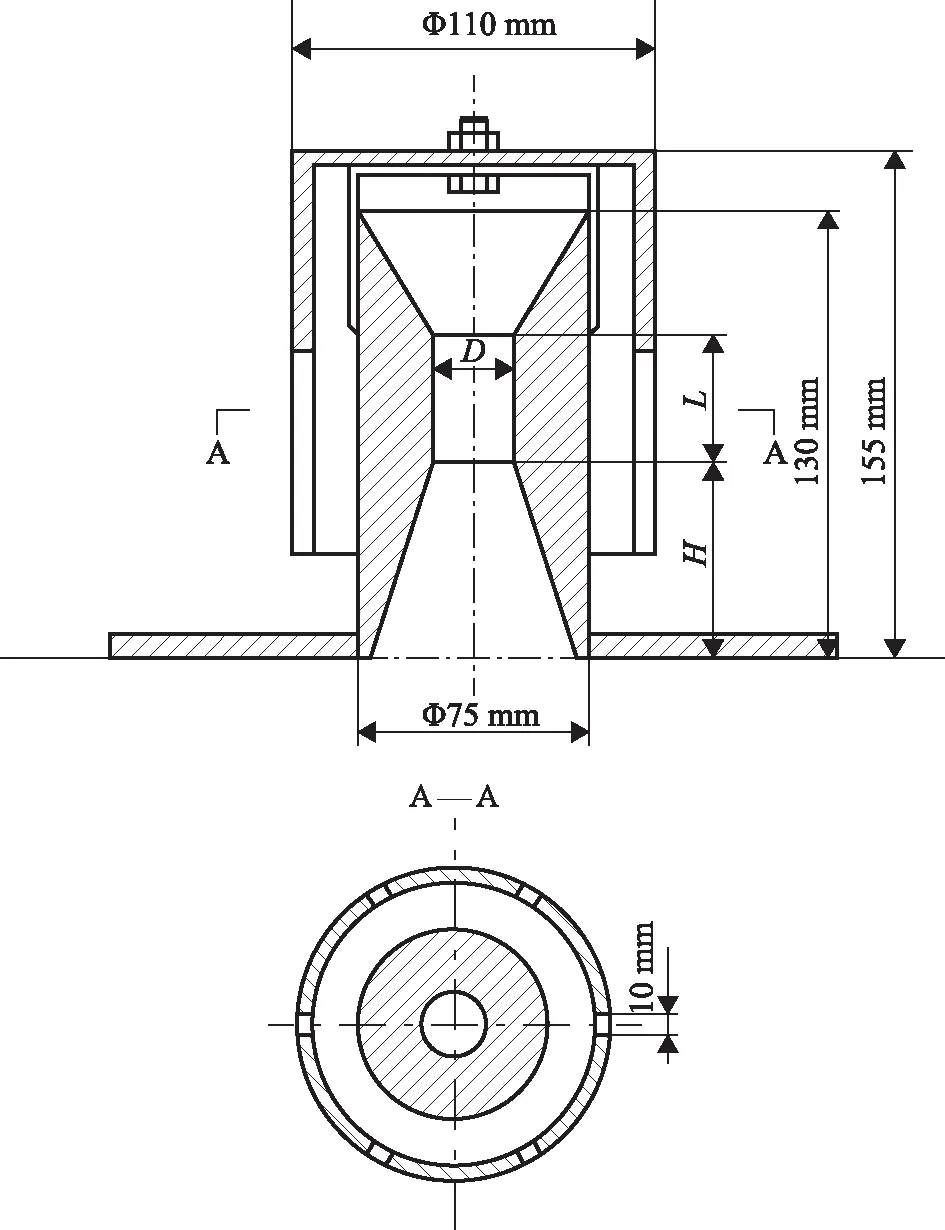
圖1 文丘里抽吸型氣液分配器結構示意

1 方法原理

1.1 SVR原理

SVR是一種基于統(tǒng)計學習理論的機器學習算法，在數據樣本量較少的情況下也能獲得良好的統(tǒng)計規(guī)律[10]。SVR的基本思想是：將線性不可回歸的樣本點經過某種非線性映射φ映射到一種高維的特征空間，使樣本可以回歸到一個最優(yōu)的高維線性平面，通俗地說就是實現線性化和升維。在SVR中，目標函數是凸的，這意味著始終可以達到全局最優(yōu)。用圖2來表示引入核函數的SVR。實際上解決非線性回歸問題便是求解權重ωi和閾值b的過程。

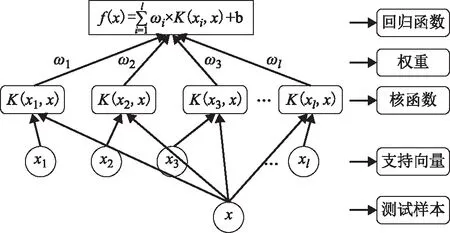
圖2 SVR示意

求解權重ωi和閾值b的過程就是求式(1)和式(2)的二次規(guī)劃問題。

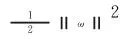
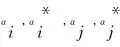
最終得到的逼近函數如式(5)所示。

(5)

樣本的非線性映射受核函數的選取影響，因此選取一個合適的核函數對SVR非常重要。目前，在SVR算法中有不同的核函數可用來選擇，分別是多項式函數、高斯徑向基函數(RBF)、Sigmoid(S形)核函數等[11]。由于RBF核函數形式簡單、支持非線性回歸，而且具備很好的泛化能力，因此本研究SVR模型選用 RBF為核函數，其表達式如下。

(6)

式中，g為核函數參數。通過改變g的值可以直接決定模型的復雜度及性能。

1.2 PSO算法

PSO算法是由Kennedy和Eberhart[12]根據鳥類捕食行為開發(fā)出的一種優(yōu)化算法。在尋優(yōu)過程中，每一個粒子都有各自的速度、位置和由目標函數決定的適應度。在迭代過程中，每個粒子都會按照個體最佳位置(Pbest)和全體最佳位置(Gbest)的最優(yōu)值更新，找到這兩個最優(yōu)值后，按照式(7)和式(8)更新粒子的速度(vid)和位置(xid)。

vid(t+1)=ω×vid(t)+c1×r1×
[Pid-xid(t)]+c2×r2×[Gid-xid(t)]

(7)

xid(t+1)=xid(t)+vid(t+1)

(8)

式中：i表示第i個粒子；d表示維度；t表示迭代次數；c1和c2表示學習因子；r1和r2表示0到1之間的隨機數；ω表示線性遞減的慣性權重；Pid表示第i個粒子在第d維上的個體極值；Gid表示所有粒子到目前為止的全局極值。在經過n次迭代后的全局最優(yōu)位置即算法尋找到的最優(yōu)解。

2 建模與優(yōu)化

2.1 基于PSO的SVR建模

2.1.1 變量選擇本研究主要針對結構參數對滴流床氣液分配器的影響，因此將3個主要結構參數(D，H，L)作為輸入變量(如圖1所示)。為了定量地分析液體速度情況，采集液體速度數據時以分配器所在平面下方 300 mm位置為采樣平面(即催化劑床層)，如圖3所示，在該平面內取一過圓心的直線，以圓心為測量點0 mm位置，沿不同的徑向半徑(R)對應的位置作為其他測量點(取0，±30，±50，±70，±90，±110 mm共11個測量點)，所以徑向半徑R也作為輸入變量。

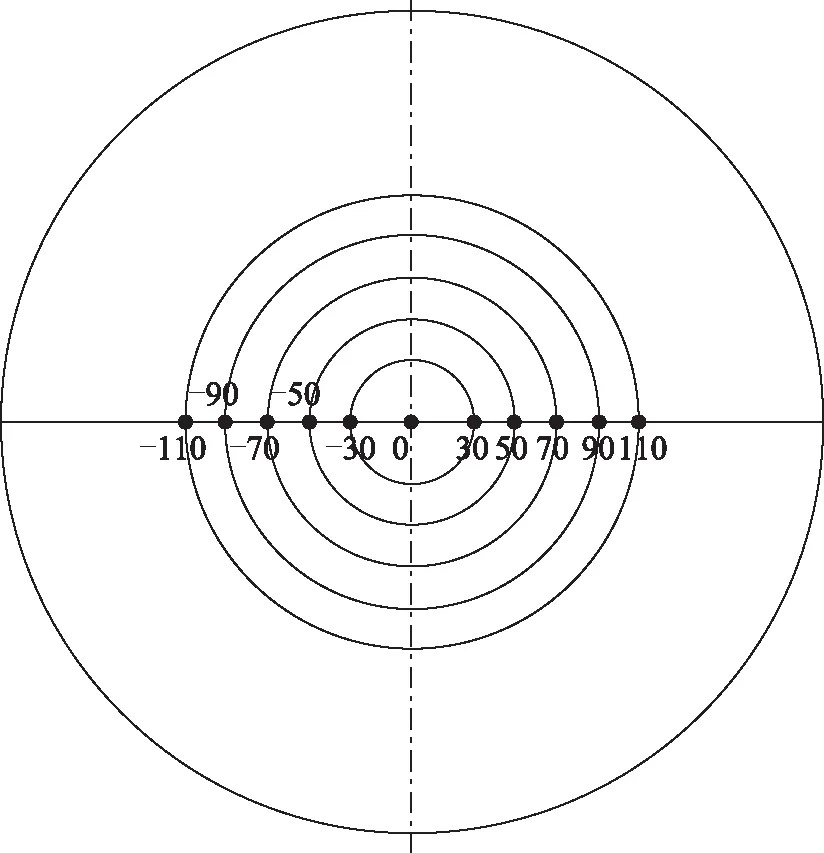
圖3 采樣平面及測量點位置示意

為了精確地定量表示液體分布均勻性，引入液體分布不均勻度的概念，定義式如下[13]。

(9)

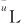
綜上所述，SVR模型的輸入、輸出變量及部分數據如表1所示。確定好輸入和輸出變量后，SVR模型訓練的目的就是找到一個合適的函數，使其滿足式(10)。

uL，i=f(D，H，L，R)

(10)

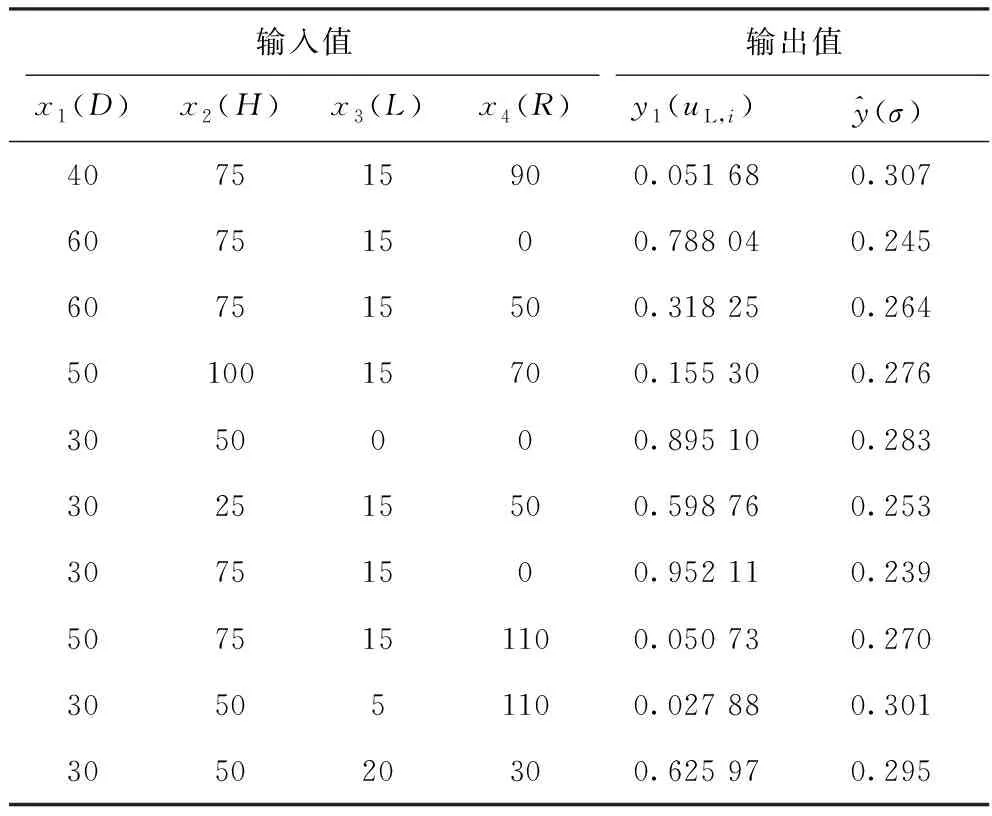
表1 SVR模型的部分樣本數據

2.1.2 基于PSO的SVR參數優(yōu)化在實際運用中，SVR的預測精度主要由懲罰因子C、核函數參數g和不敏感損失函數ε三個超參數決定[14]。僅憑先驗知識很難確定這些參數的適當值，并且手動調整參數的過程很耗時。因此，采取PSO實現參數優(yōu)化。為了提升模型預測性能，本研究中PSO算法通過5-fold交叉驗證來評估每個粒子的適應度。但是為了防止SVR模型出現過擬合的現象，在PSO過程中會給均方根誤差(RMSE)設置一個下限，當均方根誤差小于該下限時尋優(yōu)結束。

(11)

式中：n為樣本個數；yi為真實值；f(xi)為模型預測值。

本研究采用PSO對SVR參數優(yōu)化的流程如圖4所示：①初始化PSO算法的各參數(如表2所示)；②利用訓練集結合5-fold交叉驗證來計算不同參數組合對應的適應度值，作為初始的個體極值，計算全局極值；③按照式(7)和式(8)更新粒子的速度和位置，通過計算粒子的適應度值，更新個體極值和全局極值；④重復步驟③直至滿足終止條件，得到最優(yōu)的參數組合。

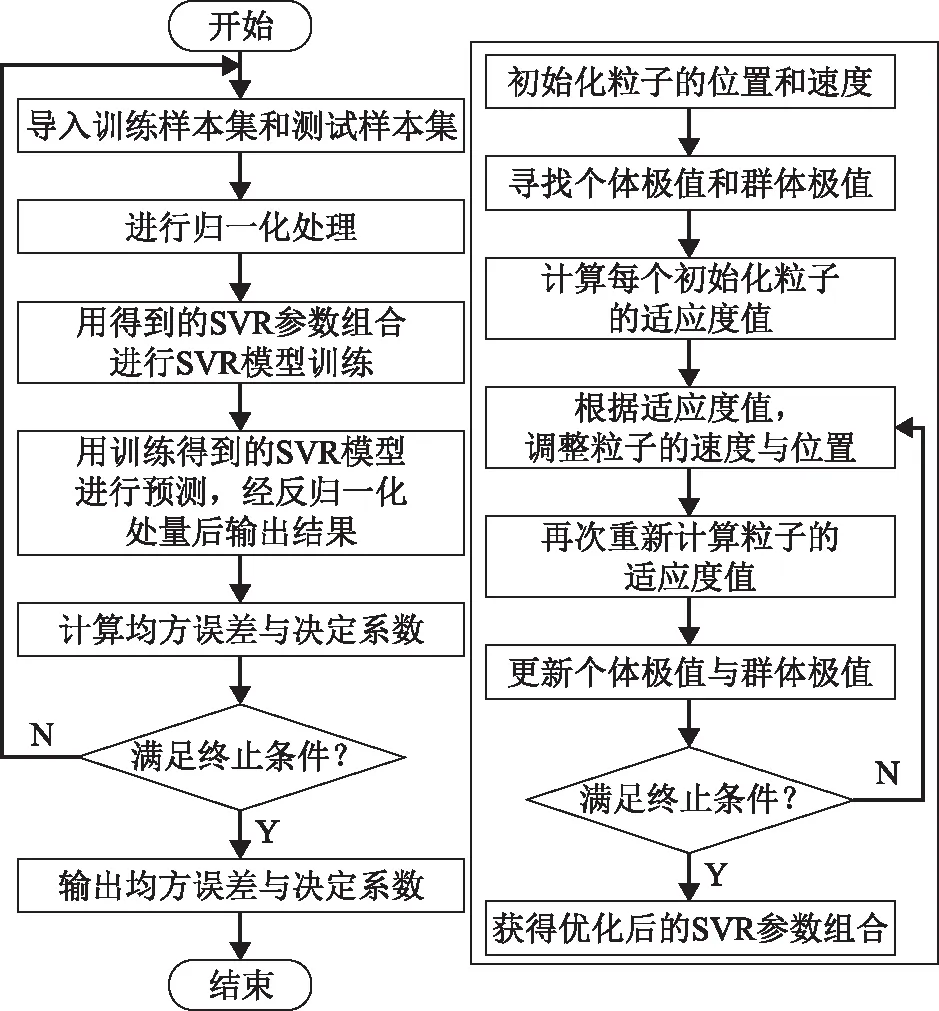
圖4 PSO-SVR流程

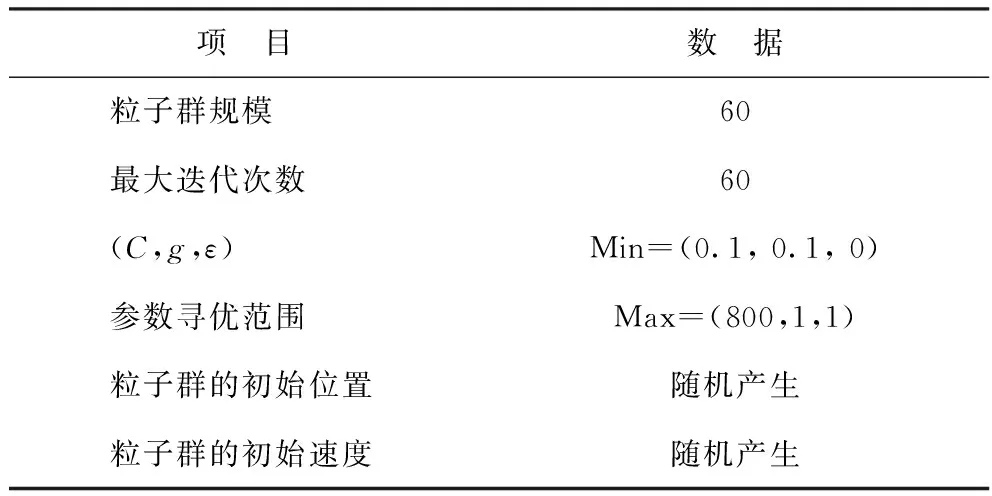
表2 PSO參數設置

利用PSO算法對ε-SVRε模型進行參數尋優(yōu)。尋優(yōu)結果隨迭代次數的改變如圖5所示。經過60次迭代后，訓練集經過5-fold交叉驗證得到的均方根誤差達到1.215×10-3，尋優(yōu)結果中C，g，ε的值分別是163， 0.737， 0.241。

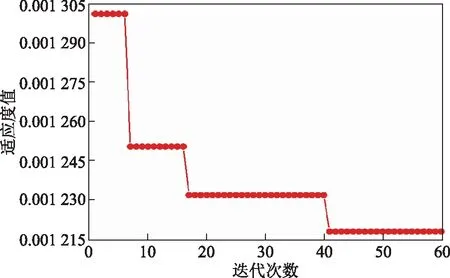
圖5 適應度曲線

2.1.3 評估參數為了評估模型的性能，引入歸一化均方誤差(MSE)和相關系數(R2)。

(12)

(13)

2.2 RSM優(yōu)化設計

RSM分析法，即響應曲面設計方法，最早由 Box 和 Wilson[15]于 1951 年提出，是通過合理的試驗設計得到一定數據，然后將數學方法和統(tǒng)計方法結合進行試驗條件優(yōu)化[16]，通過分析回歸方程來尋求最佳參數，解決多變量問題。本研究選取文丘里氣液分配器中的D，H，L為影響因素，根據文獻調研結果確定各因素的取值范圍，將三種因素的最大值與最小值輸入到 Design-Expert 設計軟件中，通過RSM中的User-Defined得到三因素五水平的53種結構組合。利用建立的PSO-SVR模型作為代理模型得到各種結構組合對應的液體分布不均勻度，結果見表3。將表 3 中的數據利用RSM法進行多元回歸擬合分析優(yōu)化，從而確定一組因素水平使響應變量達到最優(yōu)化，將最優(yōu)結果帶入CFD中進行模擬驗證。

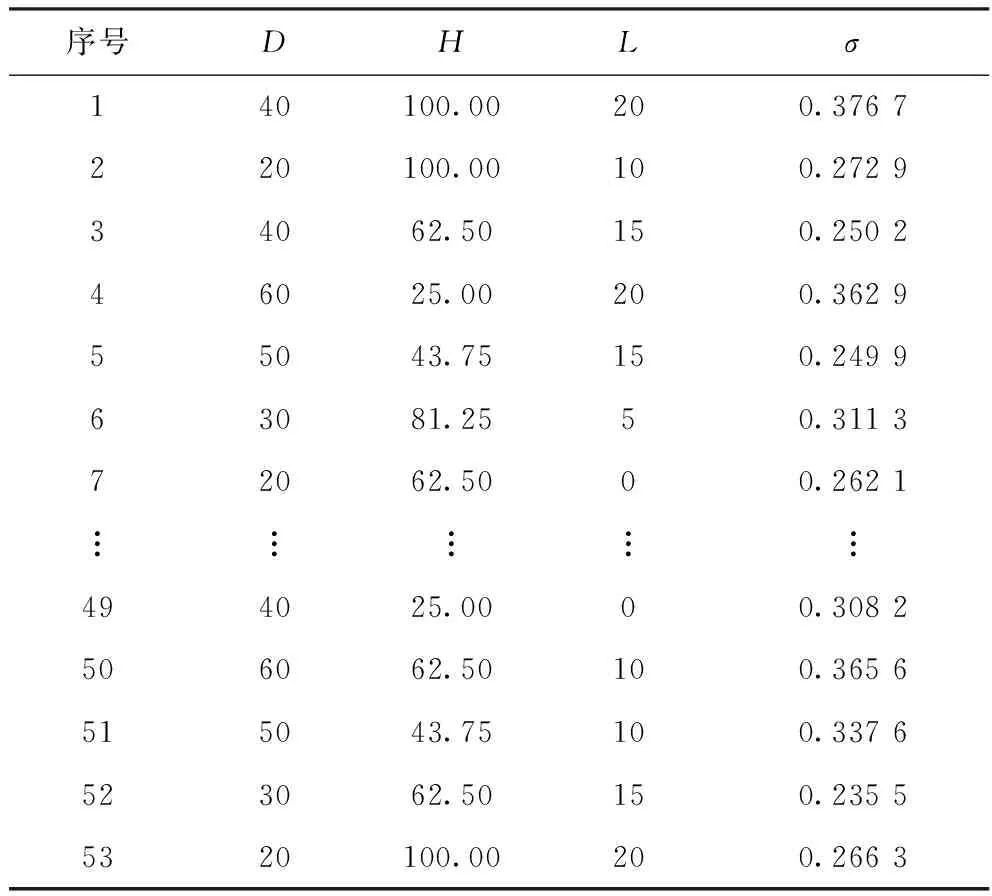
表3 RSM設計方案

3 結果與討論

3.1 PSO-SVR模型模擬結果與試驗數據對比

為了驗證算法的準確性，將PSO-SVR模型模擬結果與文獻[9]中收集的CFD試驗模擬數據進行對比，結果見圖6。由圖6可見：數據點均集中在對角線附近，表明預測結果與試驗數據一致；PSO-SVR模型對訓練集的MSE為2.364×10-4，R2為0.991，能夠達到較高的訓練精度；模型對測試集的MSE為5.391×10-4，R2為0.985，預測結果較好。說明建立的模型并沒有出現過擬合和欠擬合現象，PSO-SVR模型可以作為一種代理模型對氣液分配器的液體分布進行準確預測。

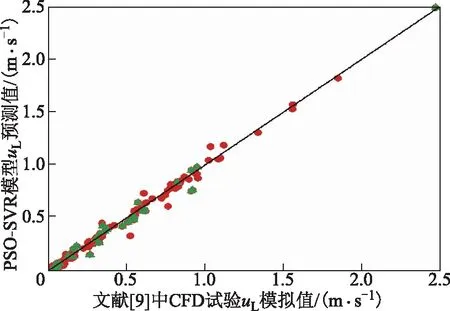
圖6 PSO-SVR模型模擬結果與實驗數據對比●—訓練樣本； ▲—測試樣本

3.2 PSO-SVR模型與SVR模型預測結果對比

利用網格搜索法優(yōu)化的SVR算法進行建模，與PSO-SVR模型進行比較，結果如表4所示。采用PSO對SVR參數尋優(yōu)的結果是{C=163，g=0.737，ε=0.241}，利用網格搜索法尋優(yōu)的結果是{C=5.656 9， g=1.071，ε=0.01}。PSO-SVR模型的MSE為5.391×10-4，R2為0.985，而SVR模型的MSE為1.314×10-3，R2為0.976。此外，利用PSO算法對SVR參數尋優(yōu)所需的時間(t=36.15 s)要比利用標準網格搜索法對SVR參數尋優(yōu)所用的時間(t=1 047 s)少很多。主要是因為在用粒子群尋優(yōu)時，當粒子群規(guī)模為60、迭代次數為60時，尋優(yōu)過程需要進行3 600次5-fold交叉驗證，而利用網格搜索法尋優(yōu)時，為3個尋優(yōu)參數設置50個水平時，整個過程需要進行125 000次5-fold交叉驗證。結果表明，經過PSO算法優(yōu)化的SVR要比網格搜索法優(yōu)化的SVR算法建立的回歸模型更加準確，泛化能力更好，并且尋優(yōu)速度更快。

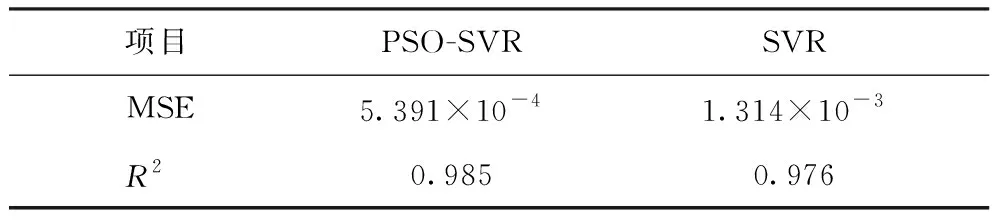
表4 PSO-SVR模型與SVR模型評估參數對比

3.3 基于PSO-SVR模型的RSM最優(yōu)結構

采用RSM法對文丘里型氣液分配器進行響應優(yōu)化，獲得優(yōu)化后的結果，如表5所示。由表5中的最優(yōu)結構參數建模，利用CFD進行模擬驗證，結果見圖7，由圖7數據和式(9)計算得到σ為0.159。將RSM法得出的σ結果以及文獻[9]中提供的最佳結構對應的σ結果與CFD模擬驗證結果進行比較，如表6所示。由表6可見：PSO-SVR結合RSM法優(yōu)化結果與CFD驗證結果的相對誤差為1.85%，說明該方法可以更好地指導氣液分布器的結構優(yōu)化設計；優(yōu)化后的分布器σ比文獻[9]中提出的文丘里型分布器的最優(yōu)結構對應的σ大幅降低。

表5 RSM最優(yōu)結果

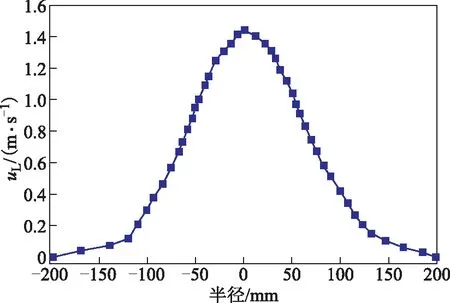
圖7 液體速度徑向分布

表6 優(yōu)化結果與CFD模擬驗證結果對比

4 結 論

(1)通過PSO進行參數優(yōu)化后的SVR模型對測試集進行預測，模型的MSE為5.391×10-4，R2為0.985，說明該模型可以很好地預測氣液分配器的液體分布。

(2)經過PSO優(yōu)化的SVR比網格搜索法優(yōu)化的SVR算法建立的回歸模型更加準確，泛化能力更好，并且尋優(yōu)速度更快。

(3)利用RSM對文丘里型氣液分布器進行響應優(yōu)化，找到了最優(yōu)結構參數組合，通過CFD驗證，進一步確認了PSO-SVR結合RSM建模優(yōu)化的可靠性，并且優(yōu)化后的分布器的σ比文獻[9]中提出最優(yōu)結構對應的σ大幅降低。