基于頻率控制的風電機組雙曲線型塔筒優化分析

文 | 張國偉，李鋼強，趙登利，焦守雷，陳江平，王子月

隨著國內風電裝機容量的增加，風能資源較優、機組安裝條件好的地方越來越少。為了彌補風能資源條件變差帶來的成本增加，風電場需要安裝具有更大風輪直徑、更高塔筒的機組，以提升發電量。另外，風電機組共振表現為葉輪轉動的激勵頻率與塔筒固有頻率交叉或重合。當風輪運行于共振區間時，機組會因發生劇烈抖動而停機，不僅影響發電量，同時也會導致塔筒的破壞、葉片的斷裂。根據機組設計應避免共振的要求，塔筒固有頻率與葉片轉動頻率避振區間至少要超過5%。

影響塔筒固有頻率的關鍵點主要有塔筒材質、結構尺寸、外部形狀等。在塔筒材質、結構尺寸確定的情況下，外部形狀對塔筒的頻率影響較大。如圖1所示，目前，市場中風電塔筒外觀結構形式主要包括全錐型、變錐型、直錐型。這些結構形式無法滿足塔筒直徑較大、塔筒較重機組的避振要求。

為克服現有技術的不足，本文提供了一種基于頻率控制的風電機組雙曲線型塔筒，通過結構優化的設計方法在塔筒底、頂部法蘭直徑及塔筒高度與壁厚的限制條件下，以塔筒強度和頻率為約束條件，采用多目標優化方法，尋求滿足機組避振要求的最優雙曲線形狀。該塔筒形式可解決傳統大直徑鋼塔頻率較高的問題。

塔筒參數化優化

本研究針對某項目的大直徑塔筒結構進行分析。由于進行本項目的塔筒設計時，基礎設計已經完成，在頂部偏航結構無法更改、機組高度為100m的條件下，采用傳統結構頻率受限，因而開展優化設計，尋求滿足要求的結構。采用有限元軟件Design Exploration多目標驅動優化模塊，建立塔筒參數化模型，以塔筒各筒節上下法蘭直徑及頂部筒節高度為參變量，塔筒一階頻率和筒節環焊縫最大應力為輸出變量，尋求滿足頻率及焊縫應力要求的塔筒結構。根據Bladed載荷仿真分析經驗，塔筒輪廓線型結構的變化對載荷影響較小，本文優化分析部分假定載荷不變，最終根據優化結果在Bladed中進行載荷迭代校對。

一、實驗參數化分析

（一）參數化模型建立

筒體的有限元網格劃分采用Solid186單元，旋轉掃掠成整體有限元模型。本計算不考慮基礎影響，底法蘭采用固定邊界約束其6個方向的自由度，無激勵。機艙采用質量點加載，假定壁厚不變。塔筒參數化模型如圖2所示。

塔筒高99400mm，底部直徑6800mm，頂部直徑5070mm，分五節，初設結構采用雙錐型塔筒。本項目所用風電機組的一階頻率設計值滿足0.270～0.279 Hz。塔筒具體參數化數值見表1，塔筒參數變量考慮塔筒制造、運輸要求。

（二）不同參變量下的塔筒固有頻率

設置參變量為D1/D2/D3/L1，輸出值為P10（塔筒的一階頻率），通過控制變量，計算得到25組參數化結構，選取其中滿足要求的5組，見表2。

由表2可知，通過減小塔筒各節直徑，可得到滿足塔筒一階頻率的塔筒結構。

（三）參變量與頻率的變化關系

表1 塔筒參變量

表2 塔筒固有頻率

輸出參變量D1/D2/D3/L1與頻率的關系，如圖3所示。

由圖3可知，隨D1/D2/D3/L1的增大，一階頻率增大。其中，D1/D2/D3與頻率呈近線性關系，L1與頻率呈曲線關系，L1值越大，對頻率的影響越小。

（四）參變量與頻率敏感性的關系

輸出參變量D1/D2/D3/L1與頻率敏感性的關系，如圖4所示。敏感性基于Spearman-Rank進行統計，同時考慮輸入和輸出參數的相關性。

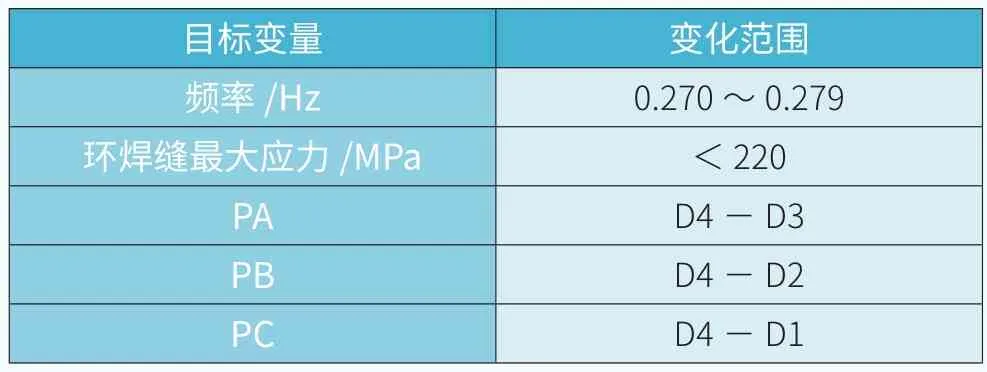
表3 目標變量

由圖4可知，各參變量與頻率的敏感性由高到低的排序為：D2/D3/D1/L1。由此可知，減小塔筒中間段直徑，更易降低塔筒固有頻率。

二、目標參數優化設計

目標參數優化設計的具體方法為先設定輸出結果的變化范圍，再進行大量的參變量分析，計算得到最接近目標結果的參變量。

根據參變量與頻率的敏感性分析結果，設定參變量為塔筒各段上下法蘭直徑，輸出變量為塔筒固有頻率和塔筒環焊縫處最大應力，參數化次數為1000次。具體目標變量見表3。

（一）目標參數結果

輸出1000次優化結果中不同參變量對應的目標參數范圍，不同參變量的頻率值如圖5所示，不同參變量的環焊縫最大應力值如圖6所示。

由圖5可知，1000次參變量優化結果中，僅有一小部分滿足頻率要求，隨著參變量變化，整體頻率分布呈現下降趨勢。由圖6可知，不同參變量下環焊縫的最大應力值范圍為153MPa～221MPa，皆滿足塔筒焊縫極限強度設計要求。

（二）目標參數分析

輸出1000次優化結果中同時滿足頻率要求及環焊縫最大應力要求的目標參數范圍，所有目標參數值如圖7所示。

目標優化算法通過不同參變量插值組合計算，得到所有的目標參數值，并尋求同時滿足目標參數的參變量組合。由圖7可知，頻率越小，對應的環焊縫最大應力越大；頻率越大，對應的環焊縫最大應力越小，滿足頻率要求的參變量對應的環焊縫最大應力較大；PA、PB、PC值越大，塔筒固有頻率越小，滿足頻率要求的參變量中，PB值的變化范圍最小，PA值的變化范圍次之，PC值的變化范圍最大，且滿足頻率要求的參變量PB值對頻率影響明顯。整體對比可知，塔筒中上段法蘭直徑越小，頻率越小。提取對應參變量數據，在滿足頻率設計要求、環焊縫最大應力較小時，參變量塔筒結構外形趨近于雙曲線型。

（三）最終優化結構設計

考慮到優化后塔筒應力較大，需增加壁厚，選用頻率最低的塔筒結構，具體尺寸見表4。

經過壁厚優化的塔筒固有頻率為0.276 Hz，滿足機組頻率的設計要求。

根據優化結果，設計的塔筒結構形式為塔筒的整體外形近雙曲線型，即連接各節塔筒的法蘭直徑符合雙曲線結構要求—以塔筒中心線為y軸，塔筒徑向方向為x軸，各筒節法蘭直徑尺寸滿足雙曲線要求。在滿足強度校核情況下，通過控制雙曲線的焦點和半實軸長可調整塔筒結構的頻率。

根據運輸條件及風電場發電要求，筒節數量不少于三節。一種五節筒節的雙曲線型塔筒結構如圖8所示，其由上下法蘭和圓錐形筒節組成，各圓錐形筒節與各法蘭焊接為圓錐形筒節。筒節一由法蘭一、法蘭二及圓錐型筒節一焊接成圓錐形筒節，法蘭一由風電機組機艙確定，法蘭二的直徑小于法蘭一的直徑；筒節二由法蘭二、法蘭三及圓錐型筒節二焊接成圓錐形筒節，法蘭三的直徑大于法蘭二的直徑；筒節三由法蘭三、法蘭四及圓錐型筒節三焊接成圓錐形筒節，法蘭四的直徑大于法蘭三的直徑；筒節四、筒節五的結構設計方法參考筒節二。連接各筒節的法蘭直徑符合雙曲線結構要求。

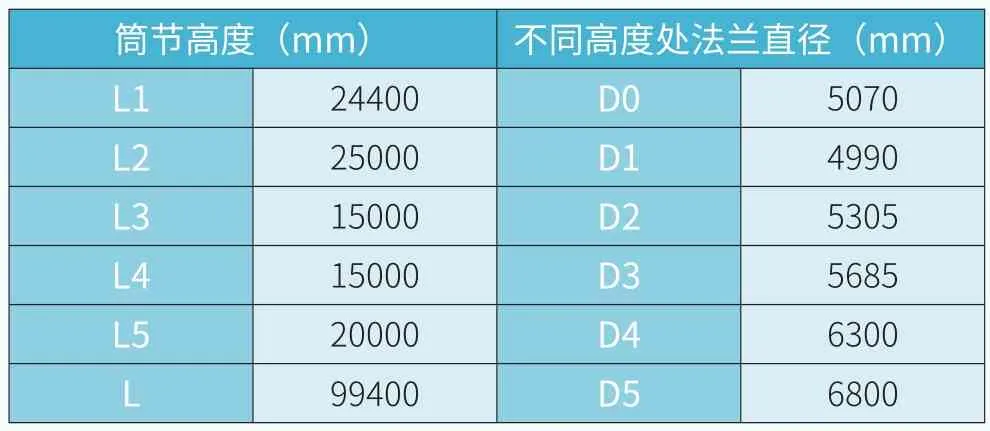
表4 塔筒尺寸

雙曲線塔筒優化算法

通過多目標優化分析結果，得到滿足工程需求的基于頻率控制的塔筒雙曲線結構。這里通過理論分析，得到基于頻率控制的雙曲線塔筒計算方法。

一、塔筒校核公式

根據風電機組設計要求，塔筒校核公式如下：

（1）雙曲線塔筒外形投影的標準表達式為：

（2）頻率要滿足以下兩個原則：

式中，fR為正常運行時的風輪最大轉頻，fR,m為m個葉片的躍遷頻率，f0,n為塔筒的第n個固有頻率。

（3）各焊縫極限強度要滿足以下原則：

式中，SF為材料安全系數，σ為焊縫正應力，τ為焊縫切應力，fyk為材料許用應力。

（4）各焊縫疲勞強度要滿足以下原則：

式中，ni,σ為應力范圍σi所對應的循環次數，Ni,σ為應力范圍σi所允許的循環次數，m為雨流計數后σi的個數。

（5）各筒體的屈曲要滿足以下原則：

式中，σx,Ed為軸向壓應力，σx,Rd為縱向設計屈曲應力，τxθ,Ed為剪切應力，τxθ,Rd為剪切設計屈曲應力，χx和χτ為標準中規定的相應屈曲折減系數。

二、塔筒固有頻率計算

簡化塔筒為懸臂梁，采用二節點梁單元進行有限元離散，設塔筒某一單元長度為l，單元密度為ρe，N為Hermite單元函數矩陣，E為彈性模量，I為截面慣性矩，A為單元截面面積。對任一單元，其質量矩陣me和彈性矩陣ket為：

由公式（7）、（8）可得：

塔筒無阻尼自由振動微分方程為：

其中，自有振動為簡諧振動，令Y(t)＝φsin(ωt＋θ)，φ是與時間無關的n階向量，ω是振動圓頻率，θ是初相位，得特征矩陣方程為：

上式為齊次線性代數方程組，有非零解的條件為系數行列式等于零，即：

通過計算可得系統的特征值矩陣和振型矩陣：

根據公式（9）―（15），可求得塔筒固有頻率f0,n的值：

其中，單元截面積為：

式中，D為單元截面直徑，t為單元截面的筒體壁厚。D值需滿足公式（1），即：

根據運輸及風電場機組要求，最大直徑D值、塔筒總高度L值均為已知。由于筒體壁厚對頻率的影響較小，設各節筒體壁厚t為固定值。確定雙曲線焦點范圍，采用多目標優化算法，滿足公式（2）、（3）、（4）、（5）、（6）的要求，即可獲得最優的雙曲線型塔筒結構。

三、雙曲線型塔筒優化算法

基于粒子群多目標優化方法，雙曲線型塔筒優化流程如圖9所示。粒子群尋優算法流程如圖10所示，其具體包括：

（1）初始化n個焦點F1和半實軸長a的粒子群，位置范圍設定為[c1－c2]和[a1－a2]，速度范圍設定為βm；

（2）判斷焦點F1和半實軸長a粒子解的可行性，根據公式（9）、（10）、（12）、（13），進行塔筒固有頻率和強度參數計算，并判斷計算結果是否滿足預設條件，即是否滿足公式（2）、（3）的頻率要求以及公式（4）、（5）、（6）的強度要求。如果有任一項要求未滿足或固有頻率和強度分析結果超出預設值，則以違反限制條件較小的粒子作為優化解；如果兩個結果均在設計范圍內，則以強度裕量最大的粒子作為優化解；

（3）根據優化解更新粒子的位置和速度。判斷是否達到最大迭代次數，如果為“否”，則跳轉至步驟（2）繼續迭代計算；如果為“是”，選擇滿足塔筒固有頻率和強度分析可行粒子解中強度裕量最大的粒子作為最優解，計算結束。

結論

本文針對某風電場塔筒結構進行分析，通過優化設計得到的雙曲線型塔筒結構，解決了采用傳統塔架結構無法滿足頻率要求的問題，并基于優化算法得到雙曲線型結構的優化方法。具體得到以下結論：

（1）通過有限元軟件進行塔筒實驗參數化分析，得到塔筒中間段直徑更易降低塔筒固有頻率，中間段直徑越小，頻率越低。

（2）通過對塔筒頻率及塔筒環焊縫最大應力計算分析可知，塔筒的頻率越小，對應的塔筒環焊縫最大應力越大；塔筒的頻率越大，對應的塔筒環焊縫最大應力越小。

（3）通過塔筒目標參數優化設計，得到1000次優化中，滿足塔筒頻率設計時，對應塔筒環焊縫最大應力較小的塔筒結構外形趨近于雙曲線型。

（4）基于粒子群多目標優化方法，以頻率和強度要求為約束條件，可得出基于頻率控制的雙曲線型塔筒優化計算方法。