自適應SA-PSO優化的威布爾混合分布參數估計方法及應用

郭 森，王大為，張紹偉，姚永超

(上海機電工程研究所，上海 201109)

0 引言

隨著裝備復雜化程度不斷提升，綜合保障成為影響其作戰使用的重要因素，而通過裝備全壽命周期數據的應用分析挖掘出故障及使用維修規律，確定預防性維修間隔，是提升其綜合保障能力的關鍵環節[1-2]。其中，根據裝備失效維護數據確定其壽命分布是重要途徑。威布爾分布是一種連續型概率分布模型，它能夠描述各種類型機械零部件失效數據的分布規律，在壽命數據分析、可靠評估和預測等方面得到了一定程度的應用[3]。對于復雜裝備而言，失效數據往往不會對各失效模式進行區分，用簡單威布爾分布并不能有效地對設備的壽命進行描述[4]。多重威布爾混合模型具有良好的擬合性能，更適合于復雜裝備失效規律的描述，但也會引入更多的未知參數，增加了模型參數估計算法的復雜度[5]。

常見的威布爾分布參數估計方法包括圖解法[6]、期望極大化(EM)法、極大似然估計(MLE)法[7]和貝葉斯法[8]等。其中：圖解法是粗略的估計，精度較低；EM算法和MLE算法需求解超越方程，在大樣本下估計精度較高，但是求解過程比較復雜，有時不易收斂，且面對截尾小樣本時偏差較大；貝葉斯法可以充分利用專家經驗、設計參數等信息提高參數估計的準確性，并且隨著使用過程中新信息的出現不斷更新結果，是解決小樣本參數估計的有效方法，但對設備先驗信息要求較高。

為了取得更精確的壽命分布模型，并減少對先驗信息的依賴性，許多學者引入了非線性擬合優化方法來對威布爾模型參數進行估計。文獻[9]將兩重二參數威布爾混合分布參數估計轉化為非線性最小二乘優化問題，并采用Quasi-Newton法進行迭代求解，能夠得到更加精確的結果，但理論要求比較高；文獻[10]采用灰色模型與支持向量機相結合的方式，解決了小樣本情況下三參數威布爾分布參數估計精度較低的問題；文獻[11]采用混合粒子群(PSO)算法對模型似然函數進行求解，避免了傳統極大似然估計方法的短板，一定程度上解決了威布爾混合分布模型的參數估計問題；文獻[12]引入模擬退火(SA)算法，直接對威布爾分布模型進行參數估計，取得了較好的結果。

針對威布爾混合分布模型復雜、參數估計難度大的問題，本文提出采用基于自適應改進模擬退火粒子群(SA-PSO)算法加以解決。將威布爾混合分布模型參數估計視為一個非線性優化問題，采用粒子群算法求解，并對粒子速度與位置更新進行自適應改進，在全局最優值的選擇上引入模擬退火機制，進一步改善粒子群算法的全局搜索能力。將改進的算法應用到某型柴油機噴油器的失效數據分析中，利用圖解法對參數初值進行粗估，用于自適應SA-PSO優化算法的種群初始化，對威布爾混合分布進行參數估計，結果表明該算法能夠有效提高參數估計的精度和效率。

1 模擬退火粒子群算法及其改進

1.1 PSO算法基本原理

PSO算法是一種用于非線性函數優化的集群智能優化算法[13]，它在解決大規模非線性問題中具有更高的優化效率和更好的優化結果。該算法將各個備選解稱為“粒子”，全部的粒子集合稱作“種群”。PSO算法首先生成初始種群，即在可行解空間中隨機初始化生成一群粒子，并根據要優化的目標函數確定與之相對應的適應度值。優化過程就是初始種群在可行解空間內部飛行，并尋找最大或最小適應度值的過程，粒子飛行的方向與距離由速度決定。

其數學過程描述如下所述。

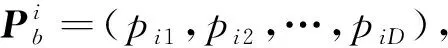
vid(t+1)=vid(t)+c1r1(pid(t)-xid(t))+

c2r2(gd(t)-xid(t))

(1)

xid(t+1)=xid(t)+vid(t+1)

(2)

1≤i≤N,1≤d≤D

c1、c2為正數，稱作加速因子,c1調節粒子飛向自身最好位置方向上的步長，c2調節粒子飛向全局最好位置方向上的步長;r1、r2為[0,1]的隨機數。

通過比較更新前后各粒子的適應度值，對單個粒子最優位置和全局最優位置進行更新，直到滿足迭代終止條件。

1.2 PSO算法的自適應改進

與其他群體智能算法相比，PSO算法概念簡單，易于編程實現求解，但在優化過程中同樣會面臨易于陷入局部極值點、搜索精度不高、收斂速度慢的問題。為此，引入慣性權重因子ω，對粒子飛行速度進行調節，提高PSO算法的收斂速度及全局搜索能力，使其能夠快速得到全局最優結果。慣性權重因子ω對速度的調節原理為

vid(t+1)=ωvid(t)+c1r1(pid(t)-xid(t))+

c2r2(gd(t)-xid(t))

(3)

由式(3)可以看出，引入的ω代表的含義主要是上一代粒子狀態對當前粒子狀態的影響程度，ω取值越大，則上一代粒子狀態對與當前粒子的狀態影響越大；反之，影響則越小。同時，算法的全局搜索能力也會隨著ω的增大而提高。因此，通過控制慣性權重因子ω的大小，可以改進粒子群算法的全局搜索能力，當ω值取為常數1時，式(3)即退化為基本粒子群算法的速度更新公式。

為了進一步提升優化性能，并加快粒子群算法的收斂速度，引入距離控制因子C(t)對慣性權重因子及加速系數進行自適應調整[14]，原理為

(4)

D為各粒子到全局最優值的平均距離；max(D)為至今平均距離的最大值；C(t)為距離控制因子，即各粒子到全局最優點的平均距離與平均距離最大值的比值。

1.3 基于模擬退火的自適應粒子群優化策略

模擬退火的思想來自常用于金屬材料提升性能的熱處理工藝退火，通過模擬高溫下金屬逐漸降溫直至熱平衡的過程，引入概率接收準則，并適當地控制溫度參數的下降，反復迭代尋找能量最小值點，最后得到問題近似的全局最優解[12]。

將模擬退火思想引入PSO算法的優化過程，改善算法在訓練過程精度降低容易發散的問題。在最優粒子的取舍中加入Metropolis準則，在接收更優粒子的同時以一定的概率接收較差粒子，能夠從局部極值中跳出，隨著溫度的降低逐漸收斂到全局最優位置。

基于模擬退火的自適應粒子群優化過程如下：

a.初始化種群中各粒子的位置和速度。

b.計算各粒子的適應度值，將當前各粒子位置和適應度值存儲在各粒子的pi中，將所有Pb中最優個體位置和適應度值存儲在pb中。

c.根據式(5)確定初始溫度t0，即

t0=f(pb)/ln5

(5)

d.根據式(6)確定當前溫度下各pi的適配值，即

(6)

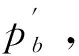
f.計算各粒子新的適應度值，更新各粒子的pi值及群體的pb值。

g.采用衰減系數法進行退溫操作，即

tk+1=λtk

(7)

h.若滿足終止條件搜索停止，輸出結果，否則返回步驟d繼續搜索。

2 威布爾分布及其參數估計方法

2.1 二參數威布爾分布

由于威布爾分布既能描述失效率上升的產品壽命，又能描述失效率下降的產品壽命，因此威布爾分布是可靠性工程中適于描述壽命分布規律的統計模型之一。

若設備壽命t服從二參數威布爾分布，則其累積失效概率密度函數、可靠度和失效率為：

(8)

(9)

(10)

β、θ分別為威布爾模型的形狀參數、尺度參數。

2.2 威布爾混合分布模型

復雜機械系統包含多個零部件，每個零部件的故障可能是在多種失效機理共同作用下發生的，而且在不同的壽命階段，不同的失效機理對系統的失效起主導作用。上述情況下，采集到的可靠性試驗數據在威布爾概率圖(WWP)上表現為曲線，如果用標準的單威布爾分布模型來描述時，會出現較大的誤差，威布爾混合分布提供了更符合實際的壽命數據擬合模型[3]。

如果1個總體由n個子體組成，設各子體的概率密度函數分別為f1(t)，f2(t),…,fn(t)，各子體的混合權重分別為p1(t),p2(t),…,pn(t)，權重之和為1，則總體概率密度函數f(t)為

(11)

若各子體都服從威布爾分布，即

(12)

βi為第i個威布爾分布的形狀參數；θi為第i個威布爾分布的尺度參數；pi為第i個威布爾分布的權重，它表示第i種失效原因或失效模式的失效數據在產品總的失效數據中所占的比例。

2.3 基于自適應SA-PSO算法的參數估計優化

對于單一威布爾分布而言，可以經過簡單的數學變換將樣本數據的非線性關系轉換線性關系，并采取線性回歸方法對數據進行擬合。但威布爾混合分布模型較為復雜，一般的數學變換無法將模型向線性問題進行轉換，因此采用非線性優化方式對其參數估計問題進行求解[15]。針對兩重威布爾混合分布模型，基于誤差平方和最小的思想，建立多參數威布爾混合分布的非線性最小二乘(NLS)優化模型。

將樣本容量為m的失效數據按壽命大小進行順序排列(t1,t2,…,tm)，采用中位秩公式計算累計失效概率的觀測值[3]，如式(13)：

(13)

(14)

根據誤差平方和最小思想構建威布爾混合模型參數非線性最小二乘優化模型，如式(15)：

(15)

采用自適應改進的模擬退火粒子群算法對威布爾混合分布參數優化模型進行求解，流程如圖1所示。在威布爾分布的參數估計方法中，圖解法參數估計值的精度較低，往往不能滿足實際使用需求，但是可以作為其他方法的迭代初值。因此，先對設備失效數據用圖解法進行求解，得到迭代初始值，之后按照基于模擬退火的自適應粒子群優化策略進行迭代優化，直到滿足終止條件。

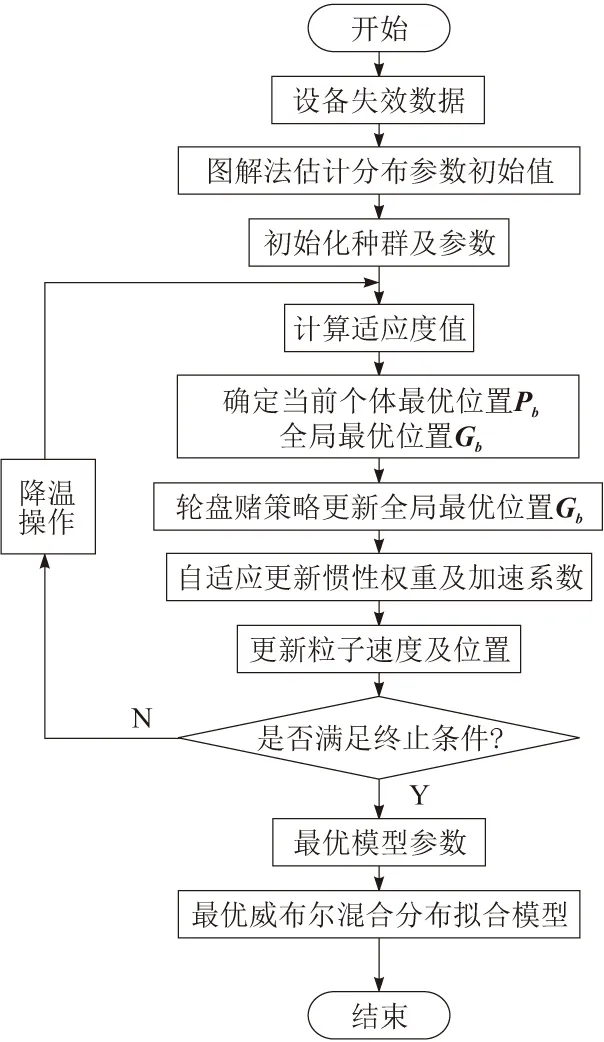
圖1 基于自適應SA-PSO的威布爾混合分布參數估計流程

3 實例分析

為了驗證本文所提方法的準確性，采用文獻[3]中某型柴油機噴油器服從兩重威布爾混合分布的故障里程進行擬合優化，其數據如表1所示。根據式(13)構造樣本集，其可靠度函數為

(16)

不可靠度為

F(t)=1-R(t)

(17)

優化目標函數為

(18)

圖解法粗估值為p=0.620 5，θ1=9 996.6，β1=1.408 5，θ2=2 250.3，β2=11.007 9。在此結果基礎上構造自適應SA-PSO優化算法的初始種群，以優化目標函數式(18)作為適應度函數按圖1所示流程進行優化。同時，為了驗證自適應SA-PSO方法的優勢，將其結果與標準PSO算法、自適應PSO算法結果進行對比。

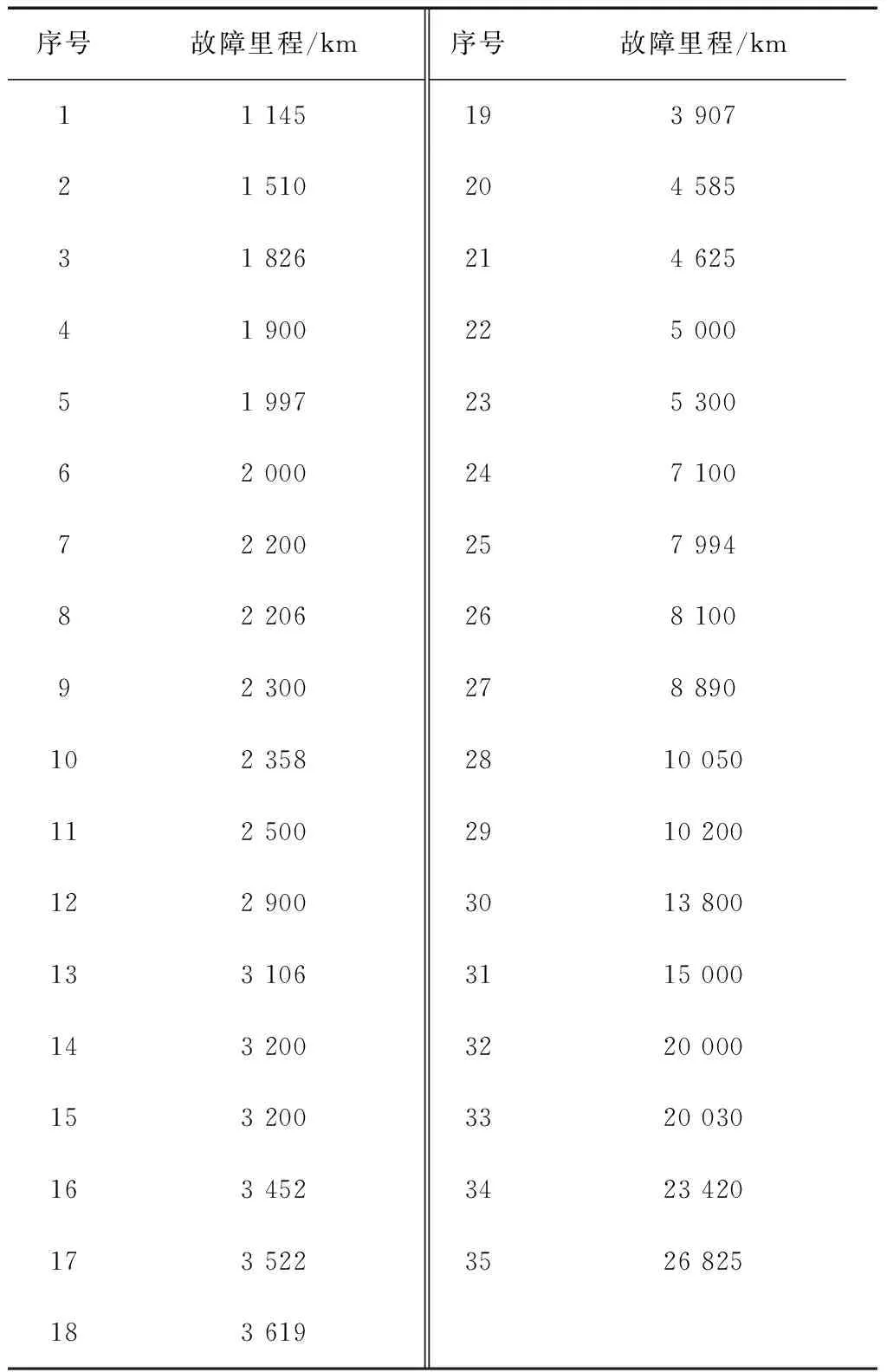
表1 某型柴油機噴油器的故障里程

3.1 自適應SA-PSO參數優化性能分析

不同優化算法對模型解決參數估計問題的優化過程如圖2所示。從圖2可以看出，標準PSO算法在迭代704步之后適應度值收斂至0.031 70，自適應PSO算法在迭代至250步時適應度值收斂至0.030 60，說明二者在收斂精度上相差不大，但后者收斂速度明顯提高；與前2種算法相比，自適應SA-PSO算法在迭代過程中，適應度值于第113步便快速達到局部極值點0.033 25，并隨后在第527步、第780步產生突變，最終收斂到0.021 00，這表明，引入模擬退火機制并經權重自適應更新的粒子群算法能夠有效跳出局部極值點收斂到更低的適應度值，具有更優的全局搜索能力以及更快的收斂速度。綜合分析，3種算法中，自適應SA-PSO算法優化性能最優，自適應PSO算法次之，標準PSO算法由于未經過任何改進，收斂速度較慢且易于陷入局部最優，優化性能最弱。

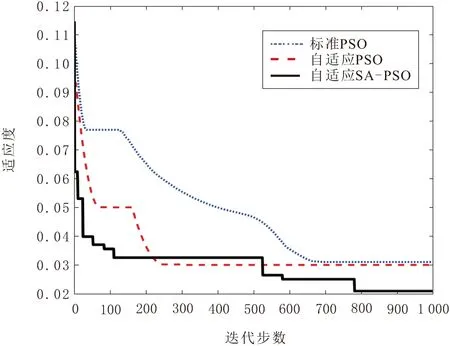
圖2 不同算法參數優化過程

3.2 威布爾分布參數估計結果分析

采用圖解法、基于Levenberg-Marquardt (L-M)的非線性最小二乘法(NLS)、標準PSO算法、自適應PSO算法和自適應SA-PSO算法，得到的模型參數估計結果及相對均方根誤差如表2所示。采用基于L-M的NLS方法得到的模型相對均方根誤差為0.089 1，通過智能優化算法擬合的模型誤差都要更小，而且隨著算法的改進，誤差也變得越來越小，其中經過自適應改進的SA-PSO算法結果最好，擬合模型的相對均方根誤差僅為0.024 8，與優化性能分析結果相符。

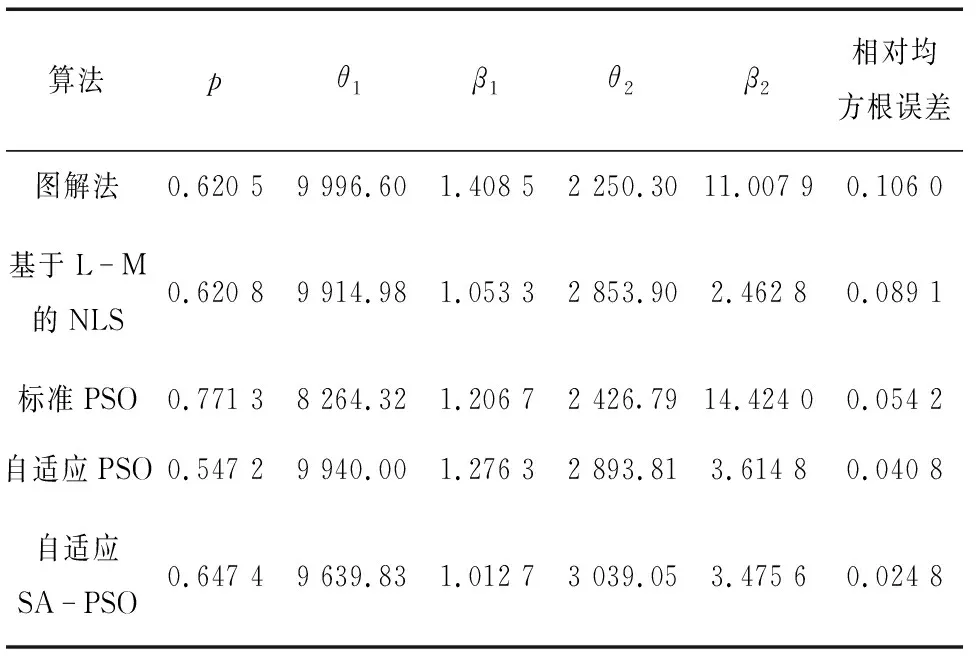
表2 不同方法參數估計結果

根據各方法參數估計結果畫出相應的模型曲線，如圖3所示。圖中能直觀看出噴油器失效數據中位秩點比較均勻的分布于相應擬合曲線兩邊。

結果表明，與傳統方法相比，基于群體智能優化算法擬合的模型具有更好的精度，其中自適應SA-PSO算法擬合精度最好。根據該算法結果得到某型柴油機噴油器的可靠度函數為

(19)

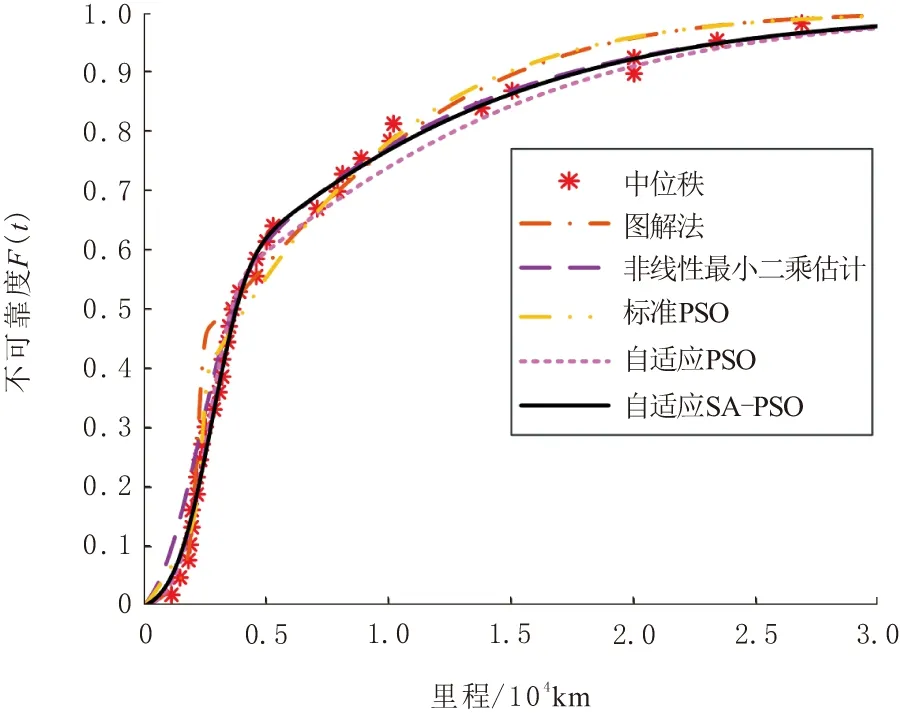
圖3 不同方法擬合曲線結果對比

4 結束語

本文對威布爾混合分布模型傳統參數估計方法進行了分析。針對模型復雜、求解難度較大的問題，在殘差最小化思想基礎上建立了多重兩參數威布爾混合分布的非線性最小二乘優化模型，并提出了一種基于自適應SA-PSO算法加以求解，最后采用某型柴油機噴油器失效數據，對本文所構造的參數估計模型及求解方法進行了驗證，可以得到如下結論：

a.與標準PSO算法及經過自適應改進的PSO算法相比，通過引入模擬退火機制對優化過程全局最優值選取進行控制，可以有效避免陷入局部最優，同時可以提高算法的收斂速度。

b.與傳統用于解決參數估計的圖解法、非線性最小二乘法相比，采用基于自適應SA-PSO算法求解威布爾混合分布模型參數的最小二乘估計值，能夠最大程度上減少先驗信息缺乏的影響，有效簡化了計算的復雜度，并且具有更高的求解精度。