基于GA-MVFOSM法的DSA250型受電弓運動可靠性分析

曹 陽，李永華，吳永鑫

(大連交通大學機車車輛工程學院，遼寧 大連 116028)

0 引言

牽引供電系統作為軌道車輛的重要動力傳輸系統，是保證列車動力來源穩定的關鍵。受電弓作為牽引供電系統的核心部件之一，其工作可靠性會嚴重影響列車運行穩定性和安全性。隨著列車運行速度的提高，受電弓工作條件逐漸惡化，對受電弓工作可靠性提出了更高的要求。因此，分析不確定性因素對受電弓工作可靠性的影響，對提高受電弓工作可靠性有重要意義。

受電弓的可靠性與其工作性能密切相關。受電弓工作性能越好，各桿件的運動軌跡越接近理想軌跡，受電弓的可靠性越高。目前，文獻[1-7]對受電弓工作性能進行了研究，這些研究多以弓網系統的結構參數為屬性建立模型，分析受電弓的工作性能是否滿足實際要求。為探究受電弓的工作性能達到實際要求的程度，有學者對受電弓的工作可靠性進行了研究。張義民等[8]采用隨機攝動法分析了受電弓在最大工作高度時的靜強度可靠性及靈敏度；李永華等[9]采用GO法對受電弓系統進行了RAMS評估，得到了受電弓系統可靠性數據；李興運等[10]和王遠霏等[11]采用系統可靠性分析的方法對受電弓系統進行了研究，得到了受電弓系統可靠性水平。上述研究得到了受電弓系統在實際運行工況下的薄弱環節，得出載荷與材料參數對受電弓靜強度可靠性的影響。除以上因素外，受電弓桿件尺寸的不確定性與運動副磨損會嚴重影響受電弓機構的運動軌跡，降低受電弓工作可靠性，造成弓網故障，威脅列車運行安全。

本文首先構建了DSA250型受電弓的運動學方程；其次根據Archard磨損理論與可靠性理論，考慮運動副磨損與桿件尺寸不確定性，建立了受電弓的磨損可靠性與運動可靠性模型；最后將遺傳算法與一次二階矩法相結合，求解受電弓運動可靠度，并分析了桿件尺寸不確定性與運動副磨損對受電弓工作可靠性的影響，為提高受電弓工作的可靠性提供一定參考。

1 受電弓運動學方程的建立

本文采用的DSA250型受電弓如圖1所示。受電弓工作原理為：升弓氣囊對下臂桿施加升弓力矩，使其繞運動副轉動，同時下臂桿通過鉸鏈的作用，帶動拉桿、連桿和上臂桿繞著相應的運動副抬升一定的角度，帶動弓頭達到規定的工作高度。平衡桿和平衡臂則在列車運行中起到保持弓頭轉角不超過允許值的作用。

圖1 DSA250型受電弓

為了保證受電弓在列車運行中可靠受流，弓頭的運動高度必須高于允許最小運動高度，若低于最小值，會嚴重影響弓網受流質量，進而影響列車正常運行。因此，獲取受電弓弓頭運動高度表達式是受電弓運動可靠性分析的前提。考慮到受電弓工作特點及力學特性，可將其簡化為平面連桿機構，如圖2所示。

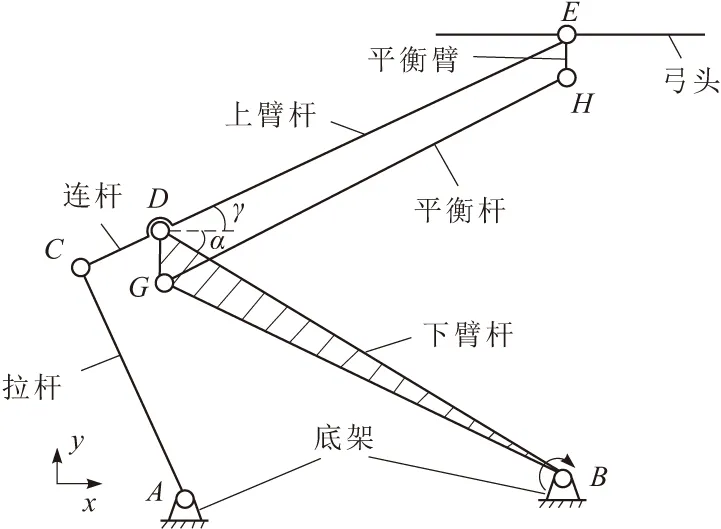
圖2 DSA250受電弓機構簡化圖

由圖2可知，弓頭E點的運動學方程可表示為

yE=lBDsinα+lDEsinγ

(1)

yE為弓頭運動高度；lBD、lDE分別為BD、DE的桿長；α、γ分別為BD、DE桿與水平方向的夾角。

2 可靠性模型的建立

根據受電弓工作要求，弓頭的運動高度需達到規定工作高度，才可以從接觸網獲取電能，使列車有穩定的動力來源。受電弓機構在反復升降弓之后，受到桿件尺寸不確定性及運動副不同程度磨損的影響，弓頭的運動高度會與規定高度有一定偏差，降低弓網受流質量，無法為列車提供穩定的動力，影響列車運行穩定性和安全性。因此,有必要分析磨損與桿件尺寸不確定性對受電弓運動可靠性的影響。

2.1 受電弓運動副磨損可靠性模型

受電弓連桿機構在運動過程中會出現運動副磨損，使運動副半徑變大，降低機構的運動精度。根據Archard磨損理論，推導出運動副半徑磨損量模型為

(2)

Δr為磨損半徑變化量；n為運動周期，本文中表示一次升弓或降弓；k為磨損系數；φ為2個構件相對轉過的角度；F為運動副的接觸力；b為運動副的接觸寬度；H為運動副材料的布氏硬度值。

由式(2)可知，運動副半徑磨損量大小受材料參數k與H影響。在實際生產過程中，受加工工藝水平的限制及人為因素的影響，材料參數具有不確定性，從而使磨損量大小也存在不確定性。根據文獻[12]，當運動副半徑磨損量達到運動副初始半徑r的0.003～0.006倍時，可認為該運動副失效，則運動副磨損可靠性模型為

(3)

μ[r]為半徑最大允許磨損量均值，其取值范圍為0.003r～0.006r；μk與μH分別為k與H的均值；σk與σH分別為k與H的標準差。

在實際運行中，受電弓受各種因素的影響使弓頭脫離接觸網的距離稱為離線距離，當離線距離小于允許值時，才可以保證受電弓正常受流。由于各運動副的磨損，必然會導致弓頭的運動高度有一定下沉。本文假設各運動副半徑的磨損量之和等于弓頭運動高度下沉量，則當下沉量小于允許最大離線距離時，可以保證受電弓正常工作。根據式(1)，弓頭的運動高度與運動副B、D、E有關，則考慮運動副磨損的弓頭運動可靠性模型為

(4)

i=B、D、E；dmax為允許最大離線距離。

2.2 受電弓運動可靠性模型

為進一步探究桿件尺寸不確定性對受電弓弓頭運動可靠性的影響，將弓頭運動高度yE與弓頭因磨損而導致的下沉量作差可得

(5)

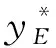
聯立式(2)和式(5)，建立考慮桿件lBD、lDE尺寸不確定性的受電弓弓頭運動可靠性模型為

β3=

(6)

μlBD與μlDE為lBD與lDE桿件的均值；σlBD與σlDE為lBD與lDE桿件的標準差；ymin為受電弓允許最小運動高度。

3 GA-MVFOSM法

受電弓運動可靠性的計算是基于可靠性理論，構建運動可靠性指標，再通過可靠度求解方法獲取運動可靠度。可靠度求解方法主要有一次二階矩法、蒙特卡洛法和高次高階矩法。其中，一次二階矩中心點法(mean value first order and second moment，MVFOSM)是工程上常用的可靠度求解方法，其原理是利用隨機變量的特征值建立結構可靠度求解模型，再通過式(7)求得結構可靠度：

R=Φ(β)

(7)

R為結構的可靠度；Φ(·)為標準正態分布的累積分布函數。

MVFOSM法雖計算簡便，精度較高，但當原功能函數較為復雜時，其計算結果往往與實際情況相差較大，如圖3所示。圖3中，β1為應用MVFOSM法求得的可靠性指標，β2為實際的可靠性指標；而且MVFOSM法展開點不一定位于原失效曲面上，會降低求解的精度。

圖3 傳統MVFOSM法的幾何意義

為提高MVFOSM法的計算精度，本文提出了GA-MVFOSM可靠度求解方法，具體求解步驟如下：

a.建立結構的可靠性模型并確定隨機變量的變化范圍。

b.按照遺傳算法的編碼規則，對隨機變量進行二進制編碼并生成初始種群。

c.以結構的可靠性模型為適應度函數，計算個體適應度。

d.根據遺傳算法的尋優原理，選取適應度高的個體進行遺傳操作。

e.由式(3)～式(7)計算結構可靠度。

綜上所述，基于GA-MVFOSM的受電弓運動可靠性分析流程如圖4所示。

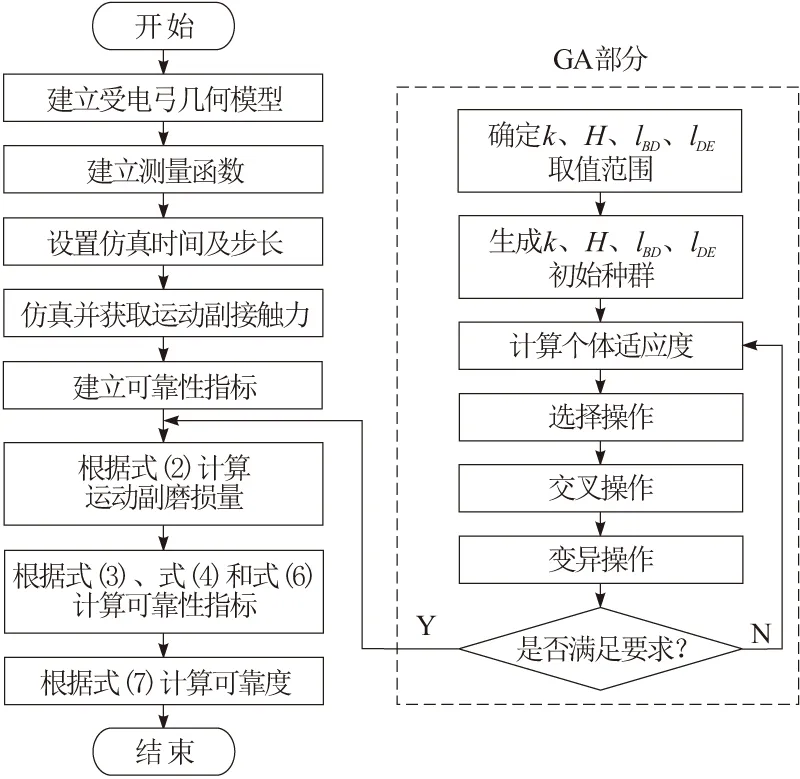
圖4 受電弓運動可靠性計算流程

4 受電弓運動可靠性分析

4.1 僅考慮運動副磨損的受電弓運動可靠性分析

對于在線路上運行的受電弓，最危險的狀態為弓頭處于最大工作高度的狀態。根據DSA250型受電弓技術參數，其最大工作高度為2 850 mm，設允許最大離線距離dmax為10 mm，允許最小運動高度ymin為2 840 mm。運動副B、D、E隨機變量分布類型及參數如表1所示，允許最大磨損量如表2所示。

表1 隨機變量分布類型及參數

表2 允許最大磨損量

為計算各運動副的磨損量，需先建立受電弓幾何模型，仿真獲取各運動副的接觸力。在ADAMS/View中，受電弓各桿件應用連桿模擬，采用長方體與布爾運算的方式建立受電弓底架與弓頭，在相應的運動副處挖孔、建立圓柱體并添加轉動副約束來模擬實際運動副銷軸，最后在運動副B處施加驅動力矩，設置仿真步長和仿真時間，模擬受電弓運動到最大工作高度。受電弓的幾何模型如圖5所示，通過仿真獲取的各運動副接觸力如圖6所示。

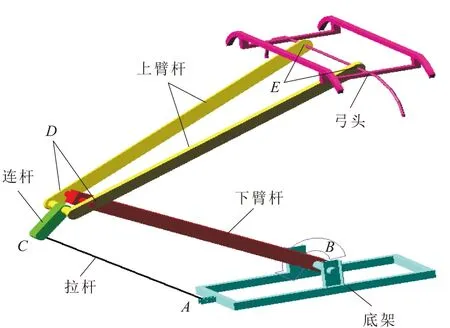
圖5 受電弓幾何模型

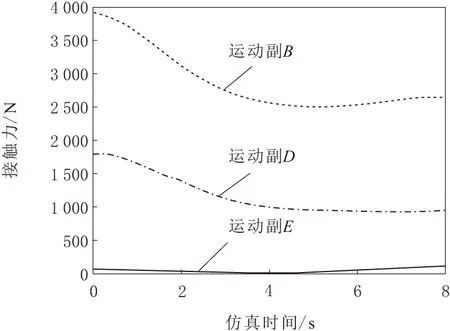
圖6 運動副接觸力

由圖6可知，運動副B與D的接觸力在0～4 s內逐漸減小，在4～8 s內變化比較平穩，而運動副E的接觸力在0～8 s內變化均較小，且運動副B的接觸力始終最大，運動副E最小。原因在于，受電弓開始升弓時需克服桿件自身重力作用，運動副B與D需較大的力來維持升弓狀態，隨著弓頭逐漸達到規定高度，二者x向距離逐漸減小(如圖1所示)，維持受電弓升弓狀態的力逐漸降低并趨于平穩，在受電弓升弓過程中，運動副B承受除底架外所有桿件重量且受有升弓力矩，運動副D承受上臂桿與弓頭的重量，而運動副E自始至終只需維持弓頭處于上升狀態，在升弓過程中，只需承受弓頭的重量，且沒有外力作用，其接觸力最小且變化比較平穩。

將獲取的各運動副接觸力及已知參數代入式(2)，得到各運動副的半徑磨損量如表3所示。由表3可知，各運動副的磨損量在GB/T 21561.1--2018規定的運動周期內，均未超過最大允許磨損量。由于運動副B的受力情況最復雜，其磨損量始終最大；運動副E的受力情況最簡單，其磨損量始終最小；運動副D的受力復雜程度介于二者之間，其磨損量也始終介于二者之間。

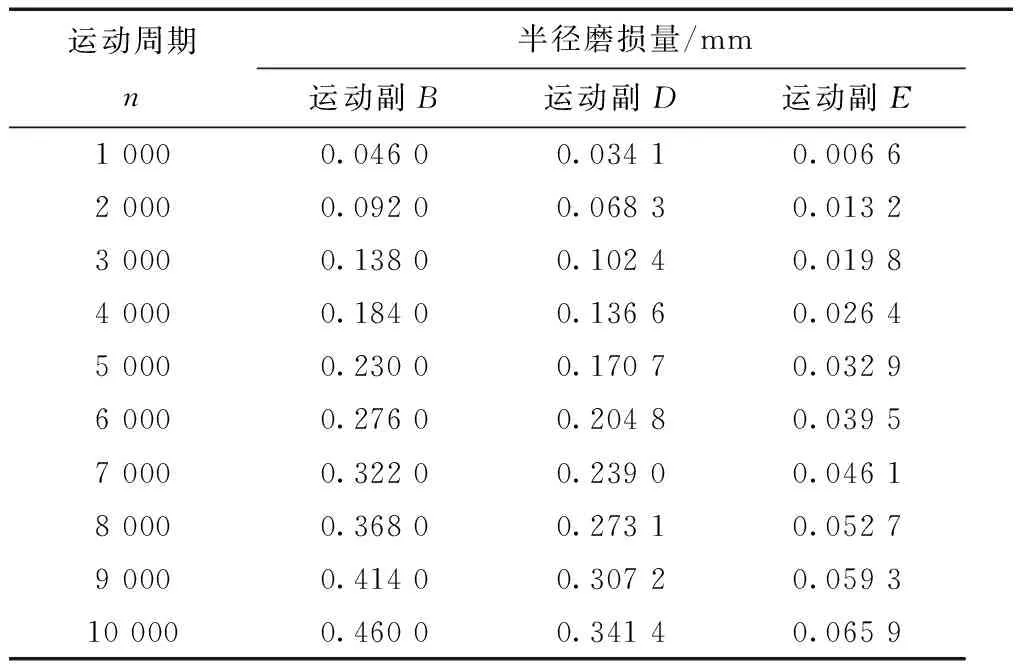
表3 各運動副的半徑磨損量

將表3數據代入式(3)得到各運動副的磨損可靠度，如圖7所示。

由圖7可知，當運動副B、D、E的磨損量分別在0～0.230 0 mm、0～0.136 6 mm、0～0.006 6 mm內時，各運動副的磨損可靠度較高，且下降速度緩慢；當各運動副的磨損量超過0.230 0 mm、0.136 6 mm、0.006 6 mm時，各運動副的磨損可靠度急劇下降。原因是當磨損量超過一定值后，各運動副半徑變大，銷軸之間的距離增加，接觸力增大，使銷軸表面接觸點在局部高壓力作用下產生黏合，在銷軸相對滑動的過程中，由于接觸表面切向力的作用，加劇了銷軸表層材料的磨損，惡化了運動副工作環境，使運動副磨損可靠度急劇下降。與MVFOSM法相比，利用GA-MVFOSM法得到的可靠度結果偏于安全，且更接近受電弓真實的可靠度值。

根據表3提供的各運動副磨損量，計算受電弓運動過程中的總磨損量，并結合式(4)和GA-MVFOSM法得到弓頭的運動可靠度，計算結果如圖8所示。

由圖8可知，隨著運動副總磨損量的增加，弓頭的運動可靠度呈現出近似線性的下降趨勢。原因在于，在受電弓機構的主要使用期間內，各運動副處于穩定磨損階段，此時運動副磨損速率恒定，運動副磨損量呈線性增加的趨勢。弓頭的運動可靠度均在0.99之上，處于較高水平，說明受電弓在1萬次的運動周期中，弓頭達到規定高度的可靠度水平較高。

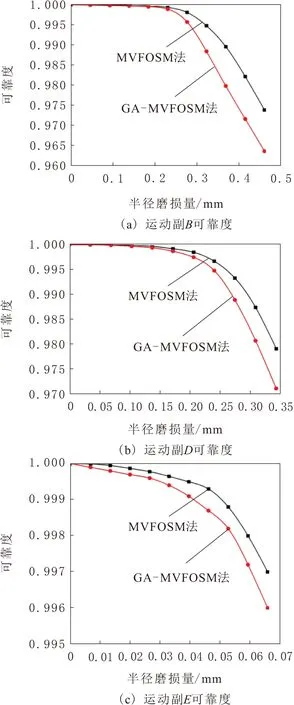
圖7 各運動副磨損可靠度

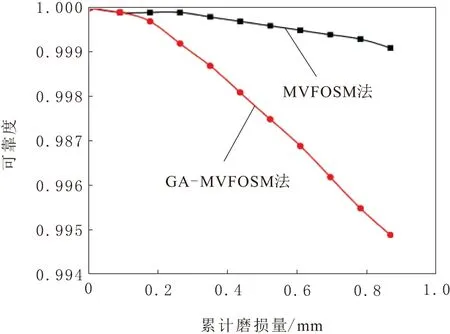
圖8 僅考慮磨損的弓頭運動可靠度對比

4.2 綜合考慮桿件尺寸不確定性及運動副磨損的受電弓運動可靠性分析

為進一步探究桿件尺寸不確定性對弓頭運動可靠性的影響，將4.1節獲得的各運動副接觸力與磨損量代入式(6)，并應用GA-MVFOSM法計算弓頭運動可靠度。其中，各隨機變量分布類型及參數如表4所示，弓頭運動可靠度結果如表5所示。

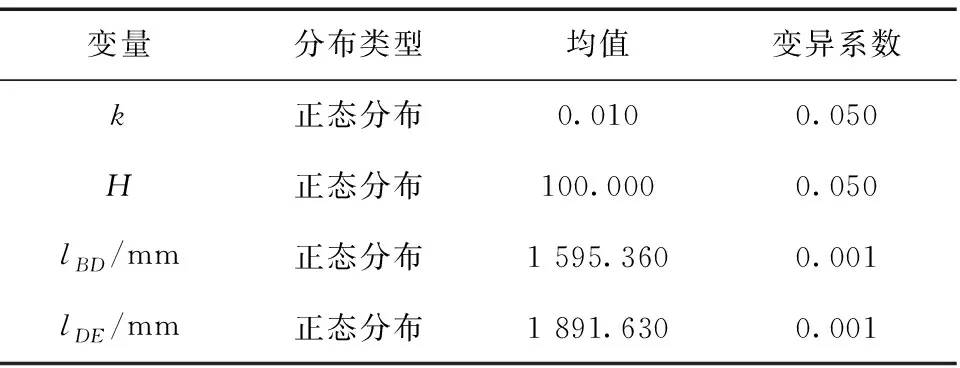
表4 各隨機變量分布類型及參數

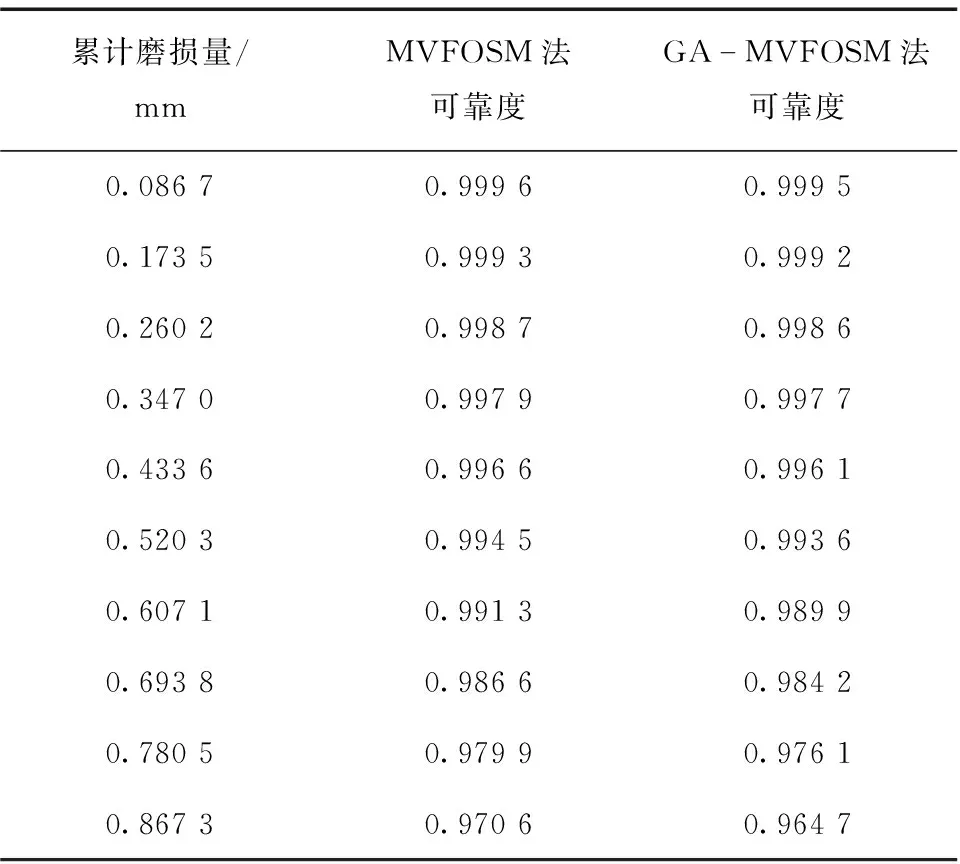
表5 弓頭運動可靠度

由表5可知，隨著運動副累計磨損量的增加，弓頭的運動可靠度逐漸降低，最小值為0.964 7。表明運動副半徑的變化影響了受電弓桿件的實際工作長度，由于這種誤差的累積，使得受電弓弓頭的運動高度逐漸偏離規定高度。弓頭運動可靠度對比如圖9所示。

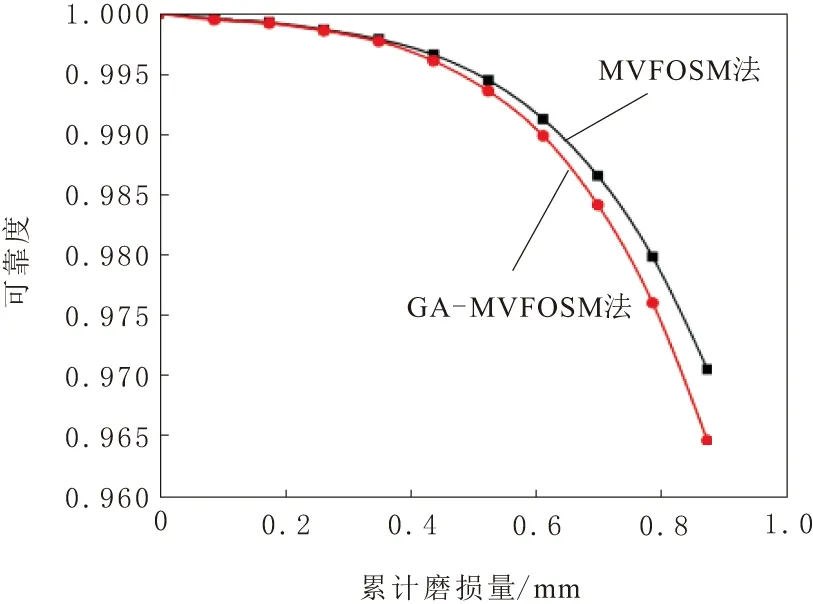
圖9 2種因素綜合的弓頭運動可靠度對比

由圖9可知，當運動副的總磨損量在0～0.433 6 mm內時，弓頭的運動可靠度下降速度較慢；當總磨損量超過0.433 6 mm時，弓頭運動可靠度的下降趨勢明顯加快，說明隨著運動副磨損量的增加，受電弓桿件實際工作長度的不確定性對弓頭運動高度的影響越來越大。為更好地比較考慮桿件尺寸不確定性后弓頭運動可靠度的變化，將通過GA-MVFOSM法獲得的2種情況下的弓頭運動可靠度進行對比，如圖10所示。

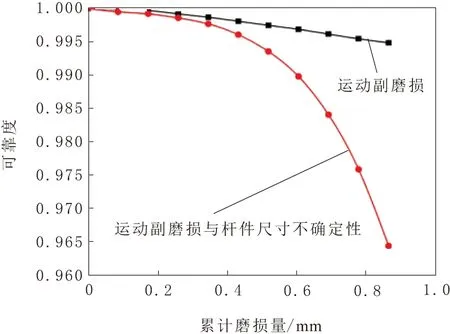
圖10 2種情況下弓頭運動可靠度對比

由圖10可知，當運動副的總磨損量在0～0.347 0 mm內時，2種情況下的弓頭運動可靠度下降速度均較為緩慢；當運動副的磨損量超過0.347 0 mm時，2種因素耦合情況下的弓頭運動可靠度下降速度要高于僅考慮磨損的情況。原因是當磨損量在0.347 0 mm內時，由于桿件尺寸不確定性造成的弓頭運動高度誤差超過允許范圍的概率較小，弓頭的運動可靠度較高；當磨損量超過0.347 0 mm時，受桿件尺寸不確定性的影響，弓頭運動高度誤差超過允許范圍的概率變大，弓頭的運動可靠度逐漸下降。因此，在實際制造與維修中，應該嚴格控制桿件的加工誤差；定期檢查運動副的磨損量是否超限；按照標準檢查弓頭是否能運動到指定高度，確保受電弓工作可靠性。

5 結束語

提出了一種GA-MVFOSM法，有效地解決了傳統一次二階矩法在功能函數復雜時線性化失效曲面與原失效曲面偏離較大的問題。

建立了運動副磨損可靠性模型，對受電弓進行運動可靠性分析。研究結果表明：當各運動副的磨損量分別超過0.230 0 mm、0.136 6 mm、0.006 6 mm時，運動副磨損可靠度下降趨勢逐漸變快；隨著運動副磨損量的增加，弓頭的運動可靠度均在0.99之上，處于較高水平。因此，為保證受電弓工作可靠性，在檢修中應重點檢查運動副磨損量是否超限。

建立了考慮磨損與桿件尺寸不確定性的可靠性模型，探究了2種因素耦合對受電弓運動可靠性的影響。研究結果表明：當總磨損量超過0.347 0 mm時，與考慮磨損相比，2種因素耦合對弓頭運動高度的影響不斷增大，使其運動可靠度不斷下降，最小值為0.964 7。因此，為保證受電弓工作可靠性，在制造中應該嚴格控制受電弓桿件尺寸的不確定性。