一種粗糙神經網絡的Simulink仿真研究

常志玲 趙旭鴿

摘要：本粗糙神經網絡由三層構成，其輸入層由上下兩個經典神經元構成的粗糙神經元組成，并與隱層之間為全連接，隱層與輸出層也為全連接，用離散并約簡后的一對輸入向量的邊界值作為輸入向量。對于這種粗糙神經網絡，利用Simulink工具進行了仿真，并詳細敘述了整個建模過程，用經典實例進行了驗證，實例表明本建模工具能夠快速準確地處理復雜的粗糙神經網絡問題，并且參數設置也比較方便。

關鍵詞：變精度粗糙集;神經網絡;Simulink;分類算法

中圖分類號：TP391 ? ? ? ?文獻標識碼：A

文章編號：1009-3044（2020）17-0007-03

Abstract： A rough neural network is made up of three layers， input layers are made up rough neurons， and each rough neuron is made up of a pair of typical neurons， and each input vector is a pair of boundary values of discrete interval of each condition attribute. The rough neurons of input layers and the typical neurons of hidden layers are linked completely， and the typical neurons of hidden layers and the typical neurons of output layers are linked completely too. The inconsistent decision table is reduced by the reduction algorithm based on variable precision rough set， and the input vectors of neural network is reduced on a large scale. It is simulinked by matlab/simulink. The experimental results show that the Simulink tool can deal with the complex rough neural network problem quickly and accurately， and the parameter setting is convenient.

Key words： variable precision rough; neural network; simulink; classification algorithm

在處理現實中的不完整性和不確定性信息方面，最有效的工具就是粗糙集理論[1]和神經網絡[2]。粗糙集理論在處理不確定性數值方面具有強大分析能力，神經網絡在處理問題方面具有高速尋找優化解的能力。但是當問題比較復雜，神經網絡輸入數據的維數就會很高，結構就比較復雜，而粗糙集理論能很好地約簡掉輸入數據的冗余，能夠把復雜問題簡單化。另外粗糙集理論的泛化性能和容錯性比較弱，但是神經網絡的泛化能力、自組織能力和抗干擾能力強，所以二者結合具有很好的互補性。因此很多人把二者結合起來進行研究，用于改善神經網絡的拓撲結構[3，4]，并取得了很好的性能。可是這些成果幾乎都把神經網絡的輸入向量問題考慮在外，實際上神經網絡的預測性能直接受輸入向量的影響。

目前，主要有兩類粗糙集理論和神經網絡的結合：一類結合由粗糙集理論先對數據約簡，去掉冗余信息，然后再構造神經網絡進行訓練[5];另一類結合通過構造粗神經元[6]，增加系統的泛化能力和容錯性能。但是兩種網絡結構都沒有考慮輸入向量的選擇問題，因此有時輸入向量的選擇不合理也會造成訓練結果的不理想。文獻[7]考慮了神經網絡的輸入向量的選擇，構造出一種新的粗糙神經網絡拓撲結構，由粗糙神經元和經典神經元混合組成，不但考慮了神經網絡的拓撲結構，而且對輸入向量做了詳細研究，能夠克服現有方法的缺點。本文在此基礎上使用Matlab中的Simulink實現了建模，并敘述了詳細的過程。

1 粗糙神經網絡

粗糙神經網絡（Rough Neural Network， RNN）[8]由粗糙神經元和經典神經元彼此互相連接而成。一個粗糙神經元[r]在神經網絡中由一對神經元組成，其中一個神經元[r]稱為上邊界，另一個神經元[r]稱為下邊界。兩個粗糙神經元之間有2個連接或4個連接，因此共有3種可能的連接，如圖1所示。上下邊界神經元之間的連線表示這兩個神經元信息的交換，其中（a）圖有4條連線，表示粗糙神經元[r]和粗糙神經元[s]之間為全連接，（b）圖和（c）圖都只有2條連線，表示有兩種連接，其中（b）圖表示粗糙神經元[r]激勵粗糙神經元[s]，（c）圖表示粗糙神經元[r]抑制粗糙神經元[s]。

粗糙神經網絡的拓撲結構和經典神經網絡的拓撲結構一樣由輸入層、隱層和輸出層組成，只是其神經元除了經典神經元還有粗糙神經元，外界的信息通過輸入層輸入，經過網絡訓練后由輸出層輸出到外界環境。

2粗糙神經網絡構造描述

為了簡化神經網絡的復雜性，首先把輸入的屬性集合進行約簡，采用的算法是基于變精度粗糙集上下分布約簡[9]，設約簡后有[m]個屬性，則輸入層L1構造[m]個粗糙神經元，由于本粗糙神經網絡對輸入向量是有選擇性的，由每個條件屬性值經離散后其區間的形成的一對邊界值作為輸入向量，如對象[i]在屬性[j]上經離散后形成的區間為[[xij，xij]]，其中[xij≤xij]，那么在第[j]個粗糙神經元輸入的數值為[xij=（xij，xij）]; 隱層L2由經典神經元構成;L1和L2之間為全連接;輸出層L3也有經典神經元構成，表示決策屬性值經訓練后的輸出，L2和L3也為全連接。所構造的粗糙神經網絡的拓撲結構如圖2，粗糙神經網絡由三層構成。具體算法的描述見文獻[7]。

3 粗糙神經網絡Simulink仿真模型的建立

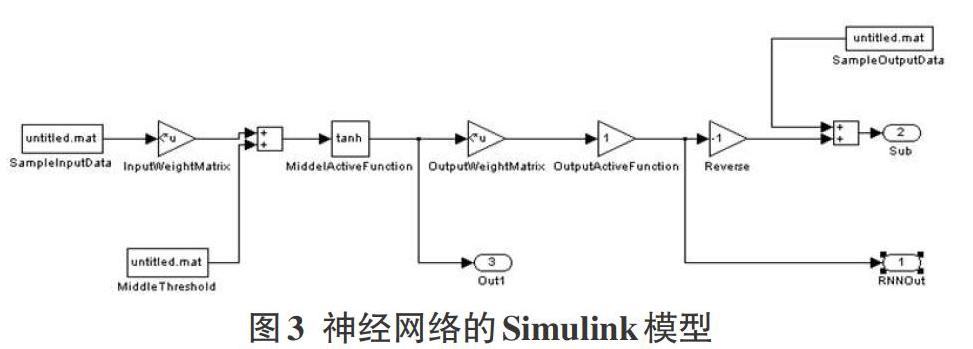
Matlab中的Simulink是非常有用的仿真工具，比如用在機器人等領域的仿真[10]，就取得了很好的效果。目前采用的神經網絡算法也很多，最常用的有BP算法，基于徑向基網絡的算法[11]。本粗糙神經網絡根據圖2所示的粗糙神經網絡的拓撲結構，使用Simulink所創建的粗糙神經網絡模型如圖3所示，采用BP算法，其中的模塊設置為：SampleInputData輸入層模塊，為輸入學習模式提供輸入接口;InputWeightMatrix是權值模塊，輸入層L1到隱層L2的連接權由初始權值隨機產生;隱層L2單元和輸出層L3單元的閾值由Middle Threshod產生;隱層L2傳遞函數模塊是MiddleActiveFunction，采用tan-sigmond型函數tansig（），根據輸入層的輸出和權值求出隱層的輸入并求出隱層的輸出，使用Out1模塊存儲隱層輸出數據;OutputWeightMatrix是權值模塊，初始權值隨機產生，為隱層到輸出層的連接權值;OutputActiveFunction是輸出層傳遞函數模塊，采用purelin（）函數，根據隱層的輸出和權值及閾值求出輸出層的輸入并求出輸出層實際輸出，并存儲在SampleOutputData模塊中，Sub減法模塊，用來實際輸出和期望輸出做比較求誤差，然后根據實際情況對權值和閾值進行調整，進行再次訓練;RUNOut模塊是實際輸出和期望輸出的誤差分析模塊。直到訓練到誤差在規定的范圍內，或滿足了訓練的次數之后停止訓練。

4實例分析

本實驗對UCI[12]數據集進行分析，選取葡萄酒數據樣本為實驗數據，其樣本共有178個，每個樣本有條件屬性13個，決策屬性1個，并利用本算法進行了規則獲取實驗。不失一般性，本實驗使用Rosetta工具從180個樣本中隨機選取60個樣本作為實驗數據，為了簡化實驗過程，隨機選取Alcohol、Malic acid、Ash、Magnesium、Total phenols、Color intensity、Hue、Proline 8個條件屬性作為數據集的條件屬性集，每個屬性值都沒有缺失值且連續，最終形成一不一致決策表。不失一般性，反復使用Rosetta隨機選取60個樣本中的36個樣本作為訓練集，剩余24個樣本作為測試集。并且對所有樣本采用GDM方法進行離散化，選取其中某一組的條件屬性離散化后的邊界值如表1所示，采用基于VPRS的上下分布約簡算法對訓練集樣本進行約簡。其中[β]的取值采用An[13]的方法，其取值為[0.5<β≤1]，[β]為正確分類率。以[β∈（0.5，0.667]]作為例子，并使用如表1所示的約簡之后的邊界值作為每一個粗糙神經元的輸入值。

針對本實例，使用圖3粗糙神經網絡進行訓練，由每個屬性的離散化后的邊界值組成的訓練樣本記為S2，測試樣本記為T2，根據S2和T2的實際情況，S2的輸入樣本含有4個條件屬性，每個樣本有4對輸入向量，因此其中輸入層根據約簡屬性集屬性設置為4個粗糙神經元，隱層神經元個數根據輸入層神經元的個數和隱層神經元的個數的關系設置成9個神經元，輸出層由決策屬性的取值決定，設置成3個神經元，分別用輸出[[100]']表示輸出第1類，輸出[[010]']表示輸出第2類，輸出[[001]']表示輸出第3類。采用本粗糙神經網絡BP算法對實例進行訓練，設定訓練次數為1000，誤差精度為[10-6]。為了計算方便，避免由于各訓練樣本的數量級差別很大以至于部分神經元達到過飽和狀態，所以對樣本的訓練集和測試集進行歸一化處理[14]，其網絡訓練誤差如圖4，經過679步達到預期目標，經分析可知，除了1個樣本外，其他樣本在[β∈（0.5，0.667]]之間都能正確分類，并且實際輸出和期望輸出的誤差趨近0，因此可以計算出其正確分類率達到95.83%。

5結束語

針對考慮了輸入向量的選擇的復雜粗糙神經網絡結構，使用了Matlab中的Simulink工具對其進行了建模，并詳細敘述了整個建模過程，用經典實例進行了驗證，實例表明本建模工具能夠快速準確地處理復雜的粗糙神經網絡問題，并且參數設置也比較方便。

參考文獻：

[1] Pawlak Z.Rough sets[J].International Journal of Computer & Information Sciences， 1982，11（5）：341-356.

[2] 楊建剛.人工神經網絡實用教程[M].杭州：浙江大學出版社，2001.

[3] 何明，李博，馬兆豐，等.粗糙集理論框架下的神經網絡建模研究及應用[J].控制與決策，2005，20（7）：782-785.

[4] 許志興，丁運亮，陸金桂.一種基于粗糙集理論的粗糙神經網絡構造方法[J].南京航空航天大學學報，2001，33（4）：355-359.

[5] 郭志軍，何昕，魏仲慧，等.一種基于粗糙集神經網絡的分類算法[J].計算機應用研究，2011，28（3）：838-840，850.

[6] Liu H J，Tuo H Y，Liu Y C.Rough neural network of variable precision[J].Neural Processing Letters， 2004，19（1）：73-87.

[7] 常志玲，王全喜.一種新的粗糙神經網絡的構造算法研究[J].計算機時代，2009（4）：52-54.

[8] 王瑋，蔡蓮紅.基于粗集理論的神經網絡[J].計算機工程，2001，27（5）：65-67.

[9] 米據生，吳偉志，張文修.基于變精度粗糙集理論的知識約簡方法[J].系統工程理論與實踐，2004，24（1）：76-82.

[10] 葉長龍，張思陽，于蘇洋，等.基于神經網絡的全方位移動機器人運動穩定性研究[J].機器人，2019，41（4）：443-451.

[11] 陳雅頌，汪曉銀，安子韓，等.PVDF分離膜性能徑向基網絡仿真模型的建立與應用[J].長江大學學報（自科版），2018，15（17）：9-14，4.

[12] The Center for Machine Learning and Intelligent Systems. UC Irvine Machine Learning Repository[DB/OL]. 2007-07-21/2007-10-07. http：//archive.ics.uci.edu/ml/datasets.html.

[13] An Ai-jun， Shan Ning， Chan Christine et al. Discovering rules for water demand prediction： An enhanced rough-set approach[J]. Engineering Applications of Artificial Intelligence， 1996， 9（6）：645-653.

[14] 柳小桐.BP網絡輸入層數據歸一化研究[J].機械工程與自動化， 2010，6（3）：122-123.

【通聯編輯：唐一東】