猜想,讓思維破繭成蝶
張大軍

[摘要]猜想是對研究的對象或問題進行類比、操作、分析、比較等,依據已有的材料知識作出符合一定的經驗與事實的推測性想象的思維方法。在數學課堂中,如果能引導學生調動自己已有的數學信息,適當運用猜想,就能幫助學生促進知識的遷移,經歷知識的形成,挖掘適合的學習方法和訓練有效的思維。
[關鍵詞]猜想;策略;類比;分析;操作
[中圖分類號]
G623.5
[文獻標識碼]A
[文章編號] 1007-9068( 2020) 29-0036-02
在一次教研活動中,我聆聽了某位新教師上的“長方體和正方體的體積”一課。教師在簡單地復習了體積的意義和體積單位后揭示課題,然后讓學生看著課題猜想:長方體的體積和長方體的什么有關系?一位學生回答:“長、寬、高。”課后,我問剛才回答的學生:“你為什么覺得長方體的體積和長、寬、高有關呢?”學生回答:“因為在長方體中我們只學過長、寬、高,所以我想應該和長、寬、高有關。”可見,教師的引導并沒有激發他的猜想。
一、思考:如何有效激發學生的猜想?
課程標準指出:“學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程。”但在實際教學中,教師往往側重于實驗、驗證猜想,而對于提出猜想的活動則輕描淡寫,導致學生想象能力不足、創造力欠缺。因此,教師在教學中要引導學生進行積極的猜想,重視培養學生的猜想能力,從而實現學生進行知識再發現和再創造。那么,怎樣才能有效地激發學生的猜想呢?
二、策略:在數學課堂中滲透猜想思想
數學猜想實際上是一種數學想象。教師在課堂上滲透猜想這一數學思想方法,從而培養學生思維的能力。
1.以類比激猜想,促進知識的遷移
小學數學的許多內容,如空間與幾何、數與代數等,都采取類比的方法進行編排。因此,教師教學時可以利用類比的方法,有意識地滲透類比思想。對于新舊聯系緊密的內容,要創設可供學生類比的情境,引導學生進行有效的猜想。
【教材研讀】“比的認識”(六年級上冊)
教學時,學生對比、除法、分數三者之間的關系已經有了非常深刻的理解,這為學生探索和發現比的基本性質打好了基礎。教材的安排加強了前后知識間的聯系,通過“想一想”的環節來啟發學生找出比中的規律,并總結出比的基本性質。因而教學時教師應引導學生用類比的方法去激發猜想。
【教學建議及操作】先復習比與除法、分數之間的關系,再舉例復習分數的基本性質和商不變性質。在類比中激發學生猜想:比有什么規律?
6 6x(
) 12 6 6÷(
)
3
=
=
=
=
8 8x( )
16 8 8÷(
)
6÷8=(6×2)÷( )=12÷16
6÷8=(6÷2)÷( )=3÷4
【反思感悟】運用類比引學生猜想,促知識遷移的教學方法必須以舊引新,使新知識與已有的知識建立聯系。因此教學時先復習比與分數、除法的聯系,分數的基本性質,除法的商不變性質等知識,為下一步的猜想和類推做好知識上的準備。通過類比,學生很快推出比的基本性質,建構出新的概念。
2.以操作悟猜想,經歷知識的形成
小學生的思維特點是以具體思維為主,教師可以結合動手操作來培養學生猜想和解決問題的能力。
【教材研讀】“認識三角形”(四年級下冊)
【教學建議及操作】讓學生理解三角形的三邊關系是本節課的重難點,建議在教學時采用“猜想一操作一猜想一驗證一發現規律”的教學模式。
師:圍一個三角形需要幾根小棒?(3根)
師:如果只有1根小棒,怎么辦?(把它剪成三段)
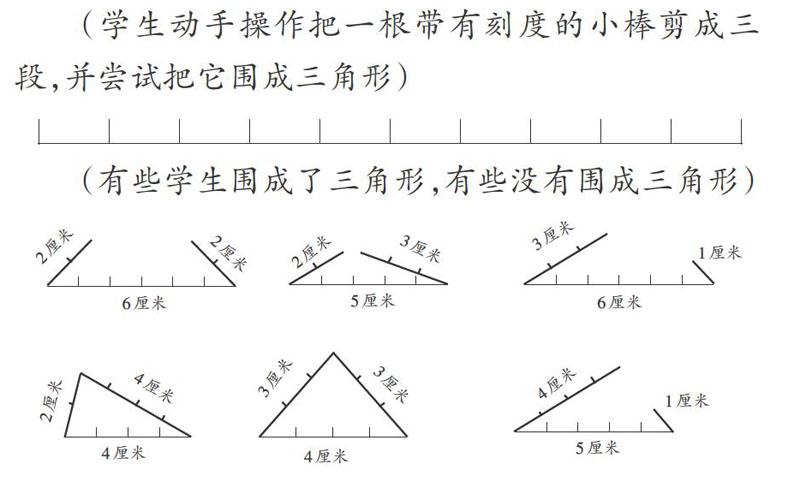
(學生動手操作把一根帶有刻度的小棒剪成三段,并嘗試把它圍成三角形)
(有些學生圍成了三角形,有些沒有圍成三角形)
師(探究圍不成的原因):想一想,為什么這樣的3根小棒圍不成三角形?
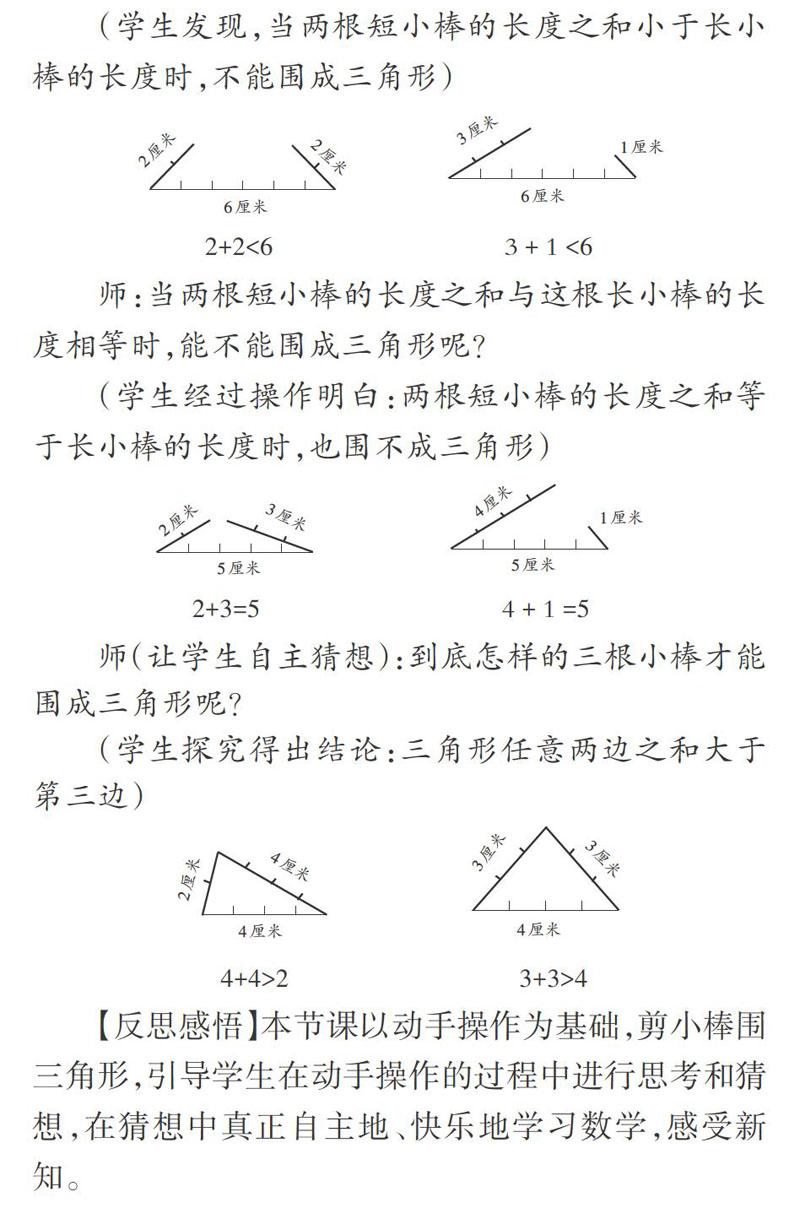
(學生發現,當兩根短小棒的長度之和小于長小棒的長度時,不能圍成三角形)
師:當兩根短小棒的長度之和與這根長小棒的長度相等時,能不能圍成三角形呢?
(學生經過操作明白:兩根短小棒的長度之和等于長小棒的長度時,也圍不成三角形)
師(讓學生自主猜想):到底怎樣的三根小棒才能圍成三角形呢?
(學生探究得出結論:三角形任意兩邊之和大于第三邊)
【反思感悟】本節課以動手操作為基礎,剪小棒圍三角形,引導學生在動手操作的過程中進行思考和猜想,在猜想中真正自主地、快樂地學習數學,感受新知。
3.以比較引猜想,訓練學生的思維
比較是一種基本思維方法,教師在教學中應該有意識地引導學生學會比較,從而發展學生同中求異、異中求同的推理思維。
【教材研讀】“長方體”(六年級上冊)
本節課的重點是探究長方體的體積計算公式,教師教學時往往側重于探究體積公式的推導,忽視對體積公式的猜想。缺乏猜想前的鋪墊,教師提出的問題只是為了猜想而猜想,流于形式,沒有給學生提供猜想的依據,導致學生盲目推測;實驗操作也是為了探究而探究,而不是學生為了證明自己的猜想而探究,削弱了學生學習的積極性。
【教學建議及操作】創設情境,利用數形結合,搭建體積與長、寬、高之間的橋梁,為接下來的猜想打下基礎。教師復習完體積和體積單位后,先提出猜想:
師:長方體的體積會與什么有關呢?
生1:與長有關。因為如果把長方體拉長,寬和高保持不變,它的體積會變大。
生2:我覺得與寬有關。因為如果讓長方體的長和高保持不變,把它拉得更寬一些,它的體積也會變大。
生3:我覺得與高有關。因為把兩個一樣的長方體上下疊在一起,長和寬都沒變,只有高變大了,它的體積也變大了。
生4:我覺得與長、寬、高都有關。因為我把8個一樣的小長方體疊在一起變成一個大長方體,這時它的長、寬、高都變大了,體積也變大了,所以我猜想長方體的體積可能與長、寬、高都有關。
教師再出示:用棱長1厘米的正方體木塊擺成下面的長方體,它們的體積各是多少?它們的長、寬、高又各是多少?
在學生說出長方體的體積后,教師引導學生觀察圖①:一個接一個地擺,從第1個正方體到第4個正方體,什么變了,什么沒變?體積呢?從圖①到圖②,什么變了,什么沒變?體積呢?從圖②到圖③,什么變了,什么沒變?體積呢?通過連續的追問,以及不同長方體相同處與不同處之間的比較,把長方體的體積與長、寬、高的關系在學生的頭腦中建立起來。建立起關系后,讓學生觀察每個長方體的體積與其長、寬、高有什么關系,并在比較后猜想:長方體的體積可以怎樣求?
【反思感悟】通過課件演示用1立方厘米的正方體拼成不同的長方體,引導學生比較幾個不同長方體,找出它們的相同點與不同點,初步感受長方體的體積與其長、寬、高之間的關聯,進而猜想并驗證長方體體積的計算公式。在這個過程中,教師引導學生確定比較的對象,通過去異求同或去同求異使學生發現知識之間的內在聯系,同時引導學生進行聯想猜測,激起學生探索新知識的興趣。
實踐證明,猜想是有效的思維方法。我們要鼓勵學生敢于猜想,訓練學生善于猜想,有效鍛煉學生的數學思維,為學生的思維掙脫“繭”的束縛,化成美麗的“蝶”。
(責編吳美玲)

