溜井中礦石壓力計算公式分析與討論

詹森昌

（江西銅業集團有限公司 德興銅礦，江西 德興 334224）

1 引言

在有條件利用重力運輸的礦山，溜井運輸系統是首選方案。它有很多重大優點，但要讓其發揮最大效益，必須對一些重大關鍵問題進行深入研究，掌握其內在規律，以便正確指導生產。溜井井筒裝有成千上萬噸礦石，是一個非常復雜的體系。礦石產生的壓力是怎樣分布的，怎樣計算的，對井壁磨損破壞有怎樣的影響，是人們非常關心的，對設計和生產管理有重要指導意義。

在分析和研究這個很復雜體系時，目前只能從宏觀方面、對有關試驗、生產中反映出來的現象進行具體的總結、分析和研究，以掌握其內在規律。

2 溜井中礦石壓力計算公式

2.1 楊森（Janssen）礦石壓力計算公式

它是目前在使用的計算公式。根據“振動放礦”［1］一書介紹，溜井中微分薄層所受的礦石壓力如圖1所示。

礦石壓力平衡方程式：

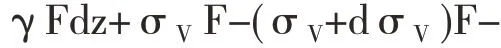
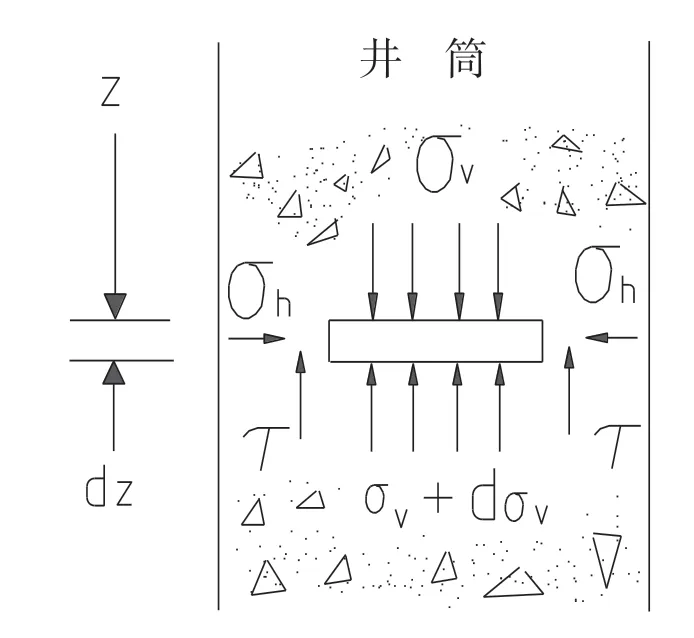
圖1 礦石作用于薄層上的力

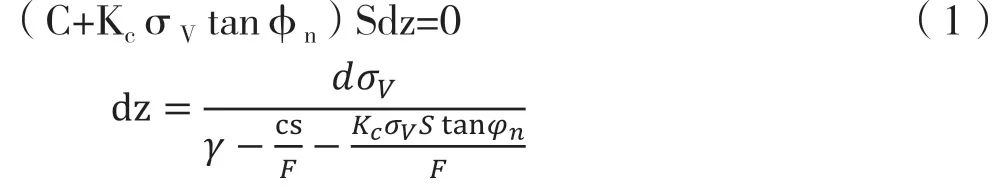
對上式積分得：

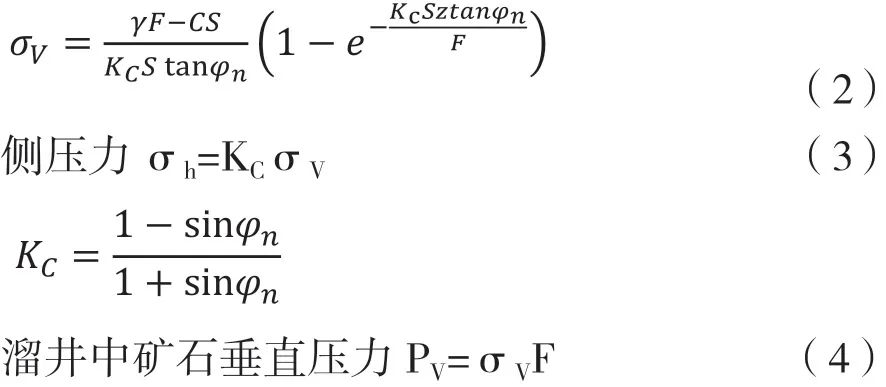
式中：σV為微分薄層壓力9.8×103Pa；γ為礦石松散體重，t/m3；F為微分薄層面積，m2；S為微分薄層周長，m；KC為側壓系數；C為礦石粘結力，Pa；Z為溜井中礦石高度，m；φn為礦石內摩擦角，度；σh為溜井中礦石側壓力9.8×103Pa；PV為溜井中礦石壓力，9.8×103N。

2.2 散體拱形礦石壓力計算公式

2.2.1 溜井底部壓力試驗

金長宇等人對放礦過程中，溜井底部壓力變化進行了數字模擬和室內試驗［2］，其試驗過程和結果如下。

（1）數字模擬試驗。

計算模型建立高度15m，直徑1m的圓形筒倉，圓筒內礦體全部為三角形，其邊長0.1m，礦體與礦體之間摩擦角35°，礦體與圓筒內壁摩擦角為5°（原文），每次放礦高度為0.5m。

試驗結論：礦體作用在底板上的壓力是恒定不變的，其壓力值沒有跟隨高度逐漸降低而出現減小現象。

（2）室內試驗。

試驗采用直徑為40mm、50mm、60mm、70mm、80mm的溜井進行了多次試驗。試驗物料為礫石，粒徑3～5mm，自然安息角為35°，密度1.52g/cm3，礫石與筒壁摩擦系數0.084（原文），裝料高度為320mm。為了消除試驗的偶然性，各種直徑的試驗重復測定10次，取平均值。試驗結果見表1。

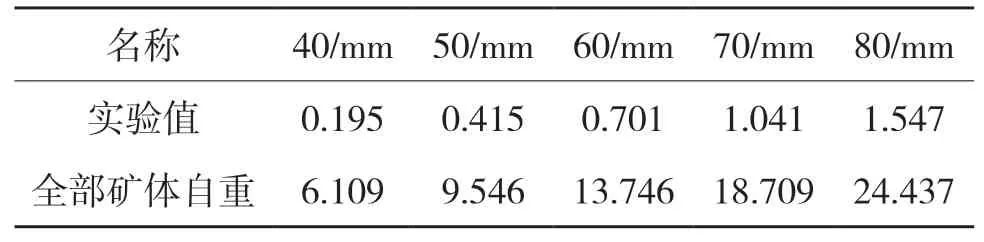
表1 各種不同直徑溜井底板壓力N

試驗結論;觀察發現，不同直徑下無論放礦高度怎樣變化，天平的讀數基本保持不變，該結論與數值模擬規律得到了相互驗證。

2.2.2 散體拱形壓力計算公式

（1）散體物料移動特性。

散體材料結構不同于連續介質材料結構，其沉降變形是在一次次的坍塌過程中完成的，散體材料結構是靠內部一系列拱結構承受、支撐上部壓力，而內部結構是自發組織起來，靠顆粒之間摩擦和擠壓來維持平衡，當拱結構不能支撐上面的重量時，就很快崩塌，內部開始自組織運動，重組新的拱結構，宏觀上表現為沉降［3］。

在放礦過程中，礦巖散體同樣出現搭拱現象，通常拱的形成和破壞交替時間短，對移動區的整體來講，表現出整體移動特征［4］。

礦巖在溜井內的移動是由于具有周期的移動拱的崩塌引起不連續現象的反復［5］。

（2）溜井底板球缺形壓力計算公式。

散體物料結構是靠內部一系列拱結構承受、支撐上部壓力。也就是說，溜井內礦石自動形成的平衡拱的拱腳未到達井壁時，拱內礦石重量是溜井底板壓力。它的形狀是一個球缺。當礦石平衡拱的拱腳到達井壁后，拱內礦石重量形成的作用力由拱腳傳遞給井壁，如圖2所示。

球缺中礦石重量Q：

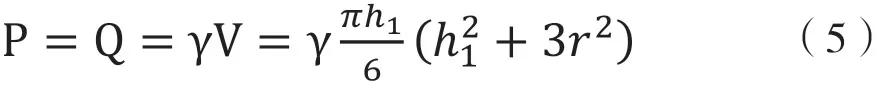
式中P為溜井底板礦石壓力，9.8×10-3N；Q為球缺中礦石重量，9.8×10-3N；γ為礦石松散體重，g/cm3；r為溜井半徑，cm；V為球缺體積，cm3；h1為球缺高度，cm。

根據表1中溜井底板壓力值，用（5）式求出球缺高度h1，見表2。

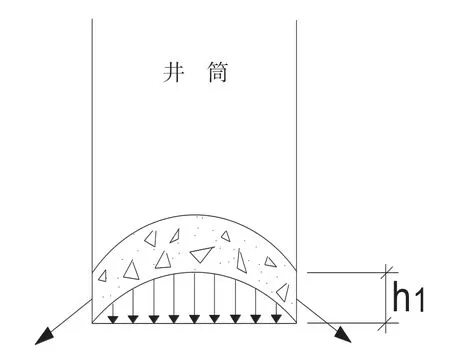
圖2 溜井底板礦石壓力

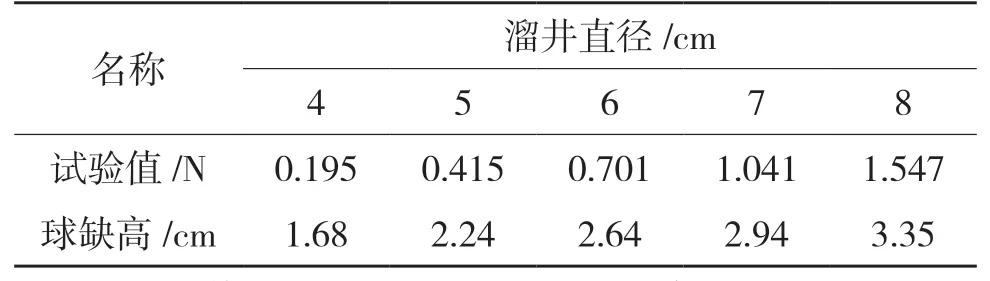
表2 不同直徑溜井的球缺高度h1

把h1值進行回歸，得出球缺高度與溜井半徑的回歸方程式：

符號意義同上。

用（6）計算出的球缺高度，反算溜井底板壓力值與試驗壓力值對比，見表3。

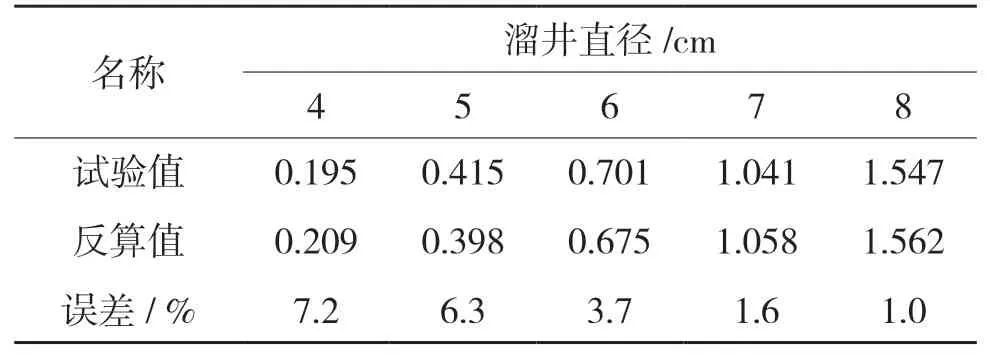
表3 試驗壓力值與（5）式反算的壓力值對比N

（3）溜井中礦石的垂直壓力和水平壓力計算公式。

溜井中礦石重量，除球缺內極小一部分由溜井底板承擔，其余礦石產生的重力是以平衡拱的形式，由拱腳傳遞給井壁，再分解成垂直向下和水平的二個分力。前者與礦石和井壁產生的摩擦阻力相平衡；后者形成對井壁的壓力，如圖3所示。

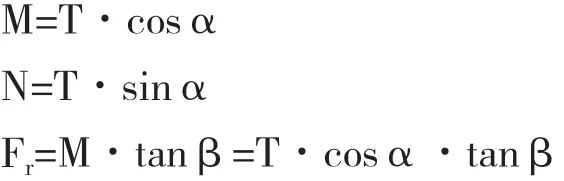
由于N力未傳到溜井井筒底板，故Fr=N

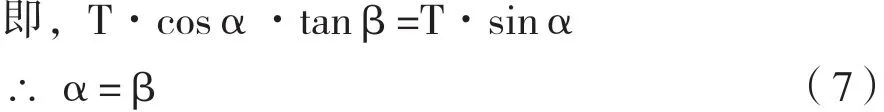
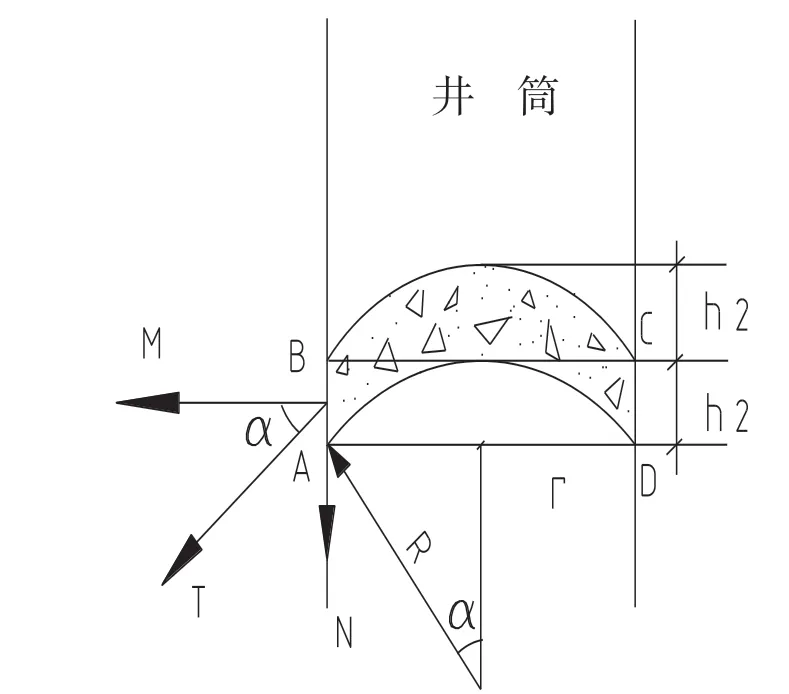
圖3 礦石的垂直與水平壓力

式中：T為平衡拱內礦石對井壁的作用力；M為T的水平分力；N為T的垂直分力；α為T的水平夾角；Fr為礦石與井壁的摩擦阻力；β為礦石與井壁的摩擦角。

由圖3得：

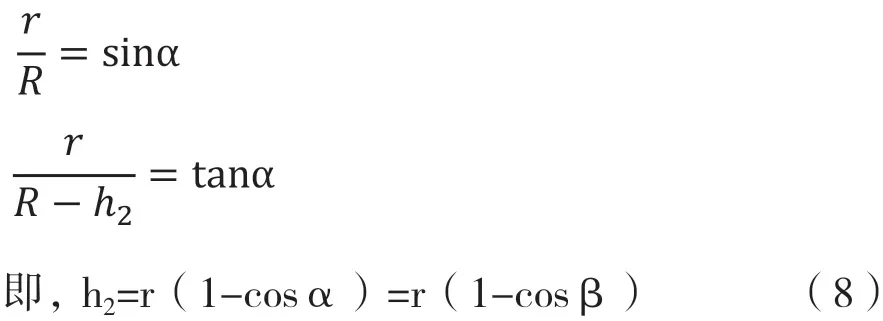
式中：R為礦石平衡拱半徑；h2為礦石平衡拱高度；其它同上。

圖3，高度為h2的平衡拱ABCD（陰影部分）礦石重量等于高度h2的圓柱體ABCD礦石重量，即：

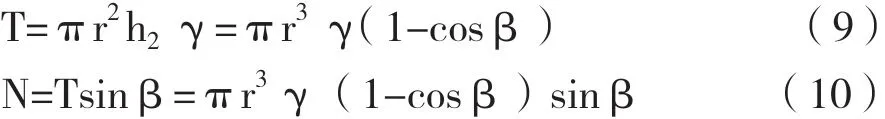
溜井中礦石作用于井壁的壓強PM：

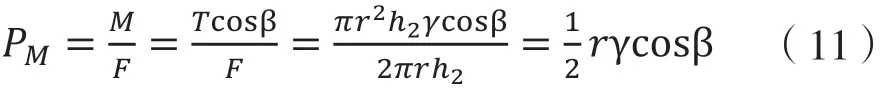
式中：PM為礦石作用井壁的壓強；其它同上。

（4）溜井中礦石壓力分布示意圖。根據上述壓力計算公式（5）、（10）、（11）作出溜井中礦石壓力與貯礦高度關系的壓力分布示意圖，見圖4。

3 溜井中礦石壓力計算與計算公式的討論

3.1 溜井中礦石壓力計算與壓力分布

3.1.1 溜井中礦石壓力計算公式匯總

以上是介紹了一個在使用的和另一個近來提出的兩個不同類型的溜井礦石壓力計算公式，其匯總為：

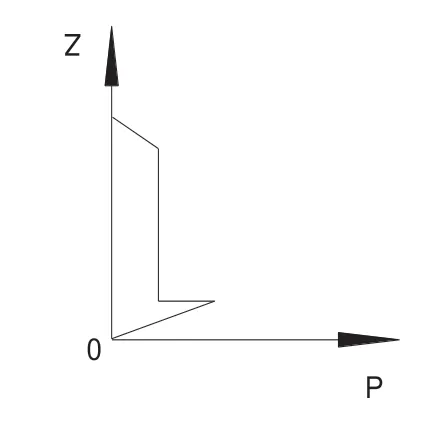
圖4 礦石垂直壓力分布示意圖

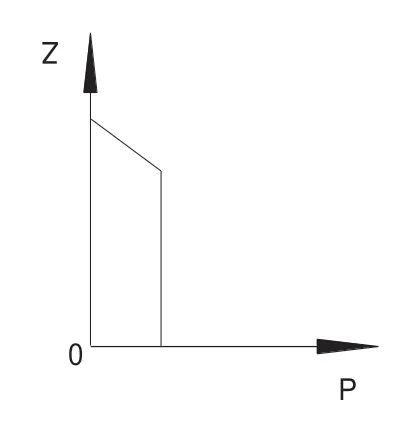
圖5 礦石水平壓力分布示意圖

楊森公式：

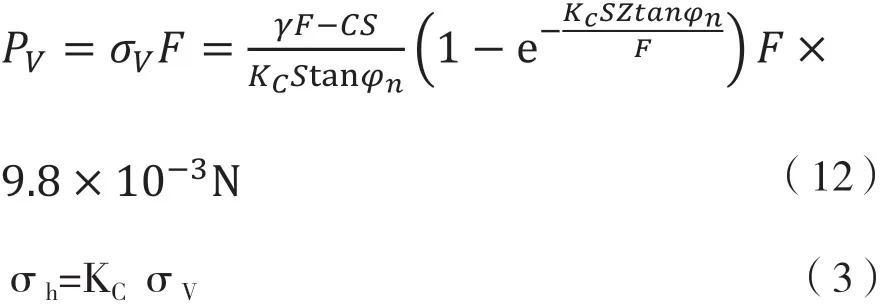
溜井散體拱形公式：

溜井底板壓力計算公式：

溜井中礦石壓力計算公式：

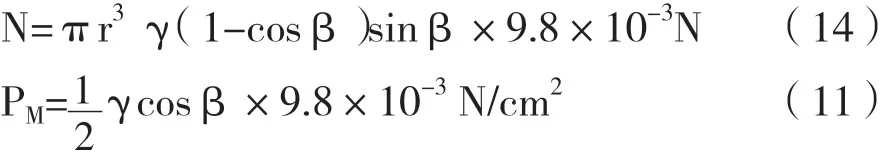
式中符號意義同上。

3.1.2 礦石壓力計算結果

為了便于比較和討論，利用上述室內試驗數據分別進行計算，設定（12）式中C=0，其計算結果見表4。

3.1.3 礦石壓力分布示意圖

（1）楊森公式壓力分布示意圖。根據表4楊森公式的數據，作出溜井中礦石垂直壓力變化示意圖6。

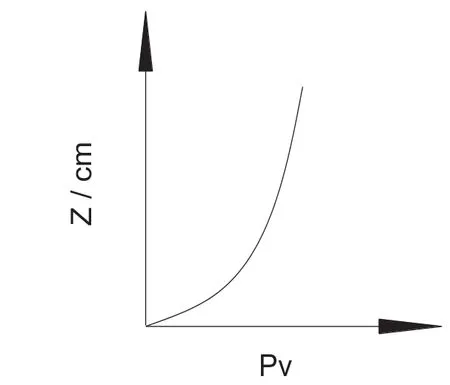
圖6 楊森壓力示意圖

由于σh=KCσV，故溜井中礦石水平壓力變化與圖6相似，其大小是KC值倍數。

（2）散體拱形公式壓力分布示意圖。見圖4、圖5。

3.2 計算數據對比

3.2.1 溜井底板壓力

根據表4，溜井底板壓力如表5。

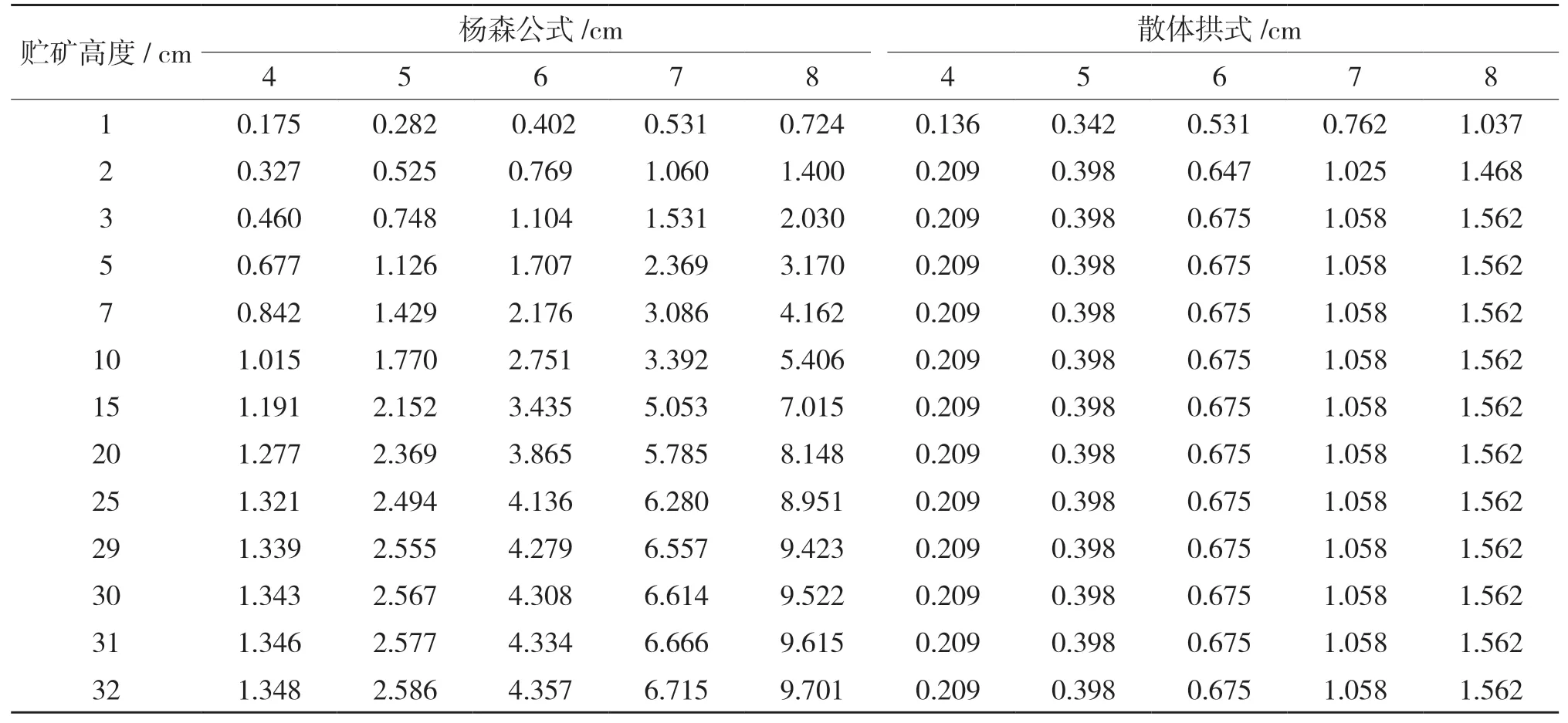
表4 不同直徑溜井內礦石壓力 N

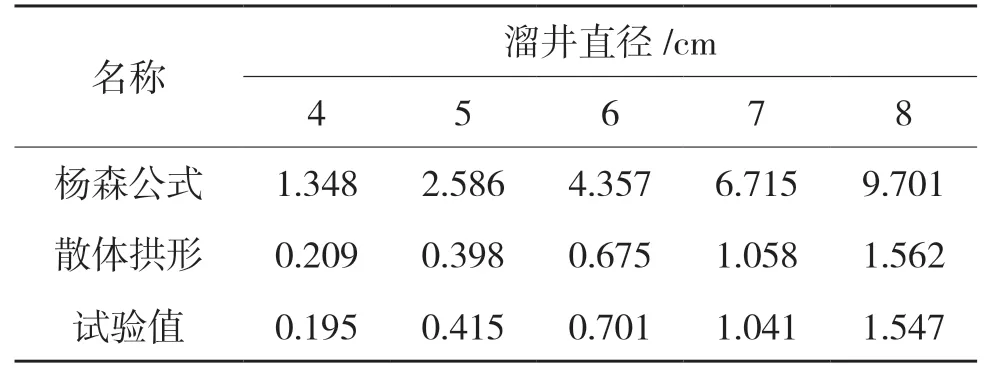
表5 溜井底板壓力N

3.2.2 溜井中礦石垂直壓力

從表4和圖6曲線看出，楊森公式計算得垂直壓力，是隨著溜井貯礦高度增加而增大；開始增大很快，后增速減小，最后接近穩定。從表4和圖4看出，散體拱形公式計算得垂直壓力，除球缺部分外，與貯礦高度無關，只是溜井半徑的函數。

3.2.3 溜井中礦石水平側壓力

楊森公式的側壓力σh=KCσV，σV是隨貯礦高度而變化的一個函數，故σh也是隨著貯礦高度而變化，其變化曲線與圖6相似。

當溜井貯礦高度達到一定高度，σV趨于穩定時，二者存在如下關系：

式中：符號意義同上。

3.2.4 二個礦石壓力計算公式分析與討論

（1）楊森公式計算出的溜井底板壓力值比試驗值大6.2～6.9倍；散體拱形公式計算出的壓力值與試驗值很接近。

（2）楊森公式計算出的礦石垂直壓力是隨貯礦高度而變化的，從表4數據看，變化范圍約7.7～13.4倍，與試驗結論不符。散體拱形公式計算出的垂直壓力是恒定的，即溜井底板反映出球缺內礦石重量，球缺上部礦石重量形成的垂直壓力，與礦石和井壁的摩擦阻力相平衡，故溜井底部壓力試驗時沒有變化，與試驗結論相一致。

（3）在溜井放礦的礦石移動“四區論”中，第一區的礦石是等速全斷面移動［4］。根據德興銅礦1號溜井放礦實測資料［6］，溜井貯礦高度為139m，第一區長度為108m，礦石平均移動速度為2.9mm/s，是平穩、緩慢下降。因此可以確定，該區內礦石壓力分布是均勻而相等的。楊森壓力公式計算結果是，溜井中上部礦石壓力是變化最大的地方，不可能產生這樣“等速、緩慢均勻全斷面”移動。只有散體拱形壓力計算公式計算結果是礦石壓力是均勻、相等分布的，才能產生這種現象。

（4）在溜井放礦過程中，隨著溜井貯礦側壓力增大，井壁磨損速度加快［7］.楊森公式計算出的側壓力是隨著貯礦高度增加而增大，溜井下部井壁受到的壓力比上部大，即溜井底部的井壁磨損應比上部大。實際上，貯礦溜井各處磨損是均勻的，與深度無關［8］.貯礦段溜井磨損均勻，上下磨損速度非常接近［9］，現實的井壁磨損與楊森公式計算結果是不相符的。

總之，楊森公式反映的溜井中礦石產生的壓力變化規律與試驗結論和生產中反映出的井壁磨損現象是不相符的。分析其產生的原因是該公式的推導過程中，未考慮散體礦石的自動搭拱效應，它改變了礦石的壓力分布規律。因此，（1）式的壓力平衡方程式是不存在的。

4 結束語

從楊森壓力計算公式推導的三點假設看，該公式是適合于大豆、小米等糧食作物和類似的物料，不適合礦山溜井中的礦石。同時，散體礦石存在自動搭拱效應，因此，溜井中微分薄層的壓力平衡方程式（1）式是不存在的。現實中溜井中礦石壓力計算是使用楊森公式，由于是其形式簡單計算方便［10］；計算結果偏大，屬保守、可靠；未能找到更合適的計算公式等原因。散體拱形壓力計算公式更適合于溜井礦石壓力計算。但溜井中的礦石是一個復雜的體系，壓力計算公式是一個重大的基礎理論問題。因此，對上述計算公式還需從試驗和生產上進一步加以證實，理論上進一步完善。