基于試驗模態分析橡膠減振件的參數識別*

曹云麗，臧傳相，余毅權

(南京中車浦鎮海泰制動設備有限公司，江蘇 南京 210000)

0 引 言

為實現結構模態分析中橡膠減振件的動力學特性的參數確認，筆者提出基于試驗模態分析法[ 1-3](EMA)進行橡膠件參數識別。試驗模態分析是通過對結構進行人為激勵，并通過對輸入及輸出信號進行處理分析、特征抽取，實現參數識別，是一種動力學結構的逆問題。隨著傅里葉變換的推廣與計算機技術的發展，試驗模態分析技術實現了飛速的發展。常見的基于頻域法的阻尼參數識別方法有半功率帶寬法、頻率細化法、峰值法、導納圓法等，基于時域法的阻尼參數識別方法有對數衰減率法、ITD法、STD法、隨機減量法等[4-6]。此外，和法家，盧曦楊，佩白等[7-8]通過直接測試法試驗研究了振動頻率、激勵振幅、預載荷與橡膠減震器動剛度的主要關系。

筆者以某軌道交通車輛用壓縮機吊掛橡膠減振器為研究對象，從動力學參數物理意義與計算原理兩方面論證了不同測試方法參數等效轉換的可行性，并通過試驗驗證參數等效轉換的準確性。

1 工作原理

通過單自由度振動系統自由振動方程推導出減振系統的模態阻尼參數(試驗模態分析法)，并通過與效粘滯阻尼參數(直接測試法)進行對比分析，建立兩種參數理論解析關系，具體如下。

1.1 動剛度參數

單自由度粘性阻尼系統主要由彈簧、阻尼器及質點組成。單自由度動力學模型如圖1所示。

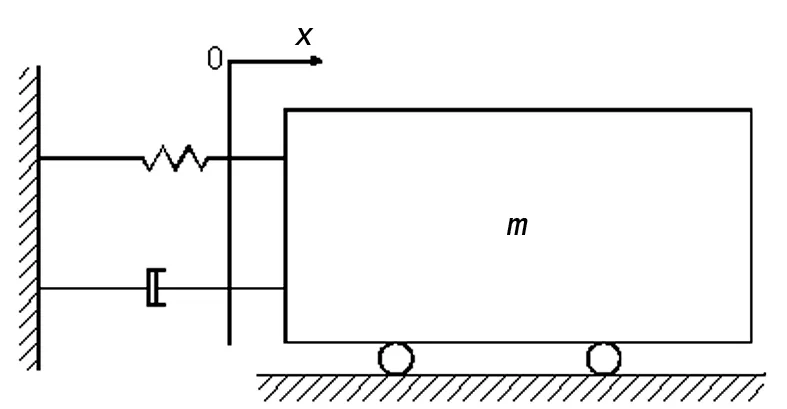
圖1 單自由度動力學模型

單自由粘性阻尼系統，其自由振動動力學方程如下：

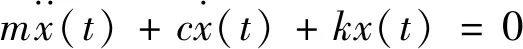
(1)

式中：m為系統質量；c為系統粘性阻尼；k為系統剛度；x為質點運動位移。

對動力學方程進行解析可知，系統的結構阻尼比為：

(2)

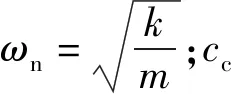
1.2 模態阻尼參數

(1) 基于時域的對數衰減法

假設系統自由振動響應為：

x(t)=Ae-ζωntsin(ωdt)

(3)

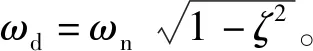
系統在某階固有頻率振動下，其結構阻尼比(即模態阻尼比)為：

(4)

式中：Ai、Ai+1為系統自由振動的第i、i+1個峰值。

(2) 基于頻域信號的半功率法

單自由度系統的振動響應在頻域內的表達式如下：

H(ω)=|H(ω)|ejθω

(5)

其中：

(6)

根據半功率法可得：

(7)

解方程(7)可知：

ω1=(1-ζ)ωn，ω2=(1+ζ)ωn

最終解得系統模態阻尼比如下：

(8)

1.3 等效粘滯阻尼參數

根據等效粘滯阻尼的力學模型，單自由系統振動周期內，從能量耗散角度計算系統等效粘滯阻尼，其表達式為：

Wd=πceqA2θ

(9)

式中：wd為系統周期振動過程中所耗散的能量；ceq為系統結構等效阻尼系數。根據系統等效阻尼系數的物理意義，振動系統周期耗散能量即為振動系統應力-應變滯回曲線所圍成面積，如圖2所示。

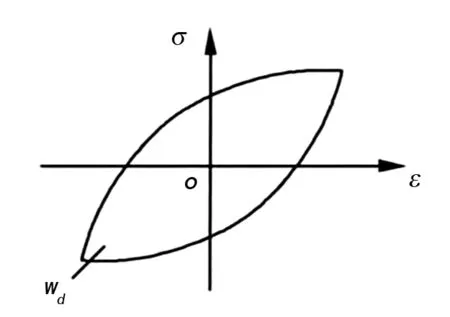
圖2 結構應力-應變滯回曲線

故結構阻尼比可通過如下計算：

(10)

式中：ceq為系統等效粘滯阻尼；w為系統振動頻率。

在振動系統在某固有振動頻率下，減振件的結構等效阻尼參數可通過試驗模態阻尼參數反向求得。

2 試驗模態分析法測試

2.1 試驗裝置

為實現橡膠減振件模態參數快速識別，又不失一般性，根據基本原理建立自由度較少的彈簧-阻尼-質量的試驗方案，彈簧及阻尼器由橡膠減振件承擔，橡膠減振件選用某成熟工業產品。

試驗設備采用法國OROS 32通道動態信號采集儀、美國PCB模態調諧力錘以及PCB三向加速度傳感器，模態參數識別采用南京航空航天大學自主開發的N-modal模態分析軟件。具體試驗裝置如圖3所示。

圖3 彈簧-阻尼-質量系統試驗裝置

2.2 試驗方案

實驗分別對43.80 kg、62.50 kg、81.45 kg、100.40 kg、125.25 kg的質量塊進行了實驗。由于質量塊的結構較為簡單，在鐵塊上表面均勻分布4個測點(處于表面四個頂點位置)，測試位置如圖4所示。

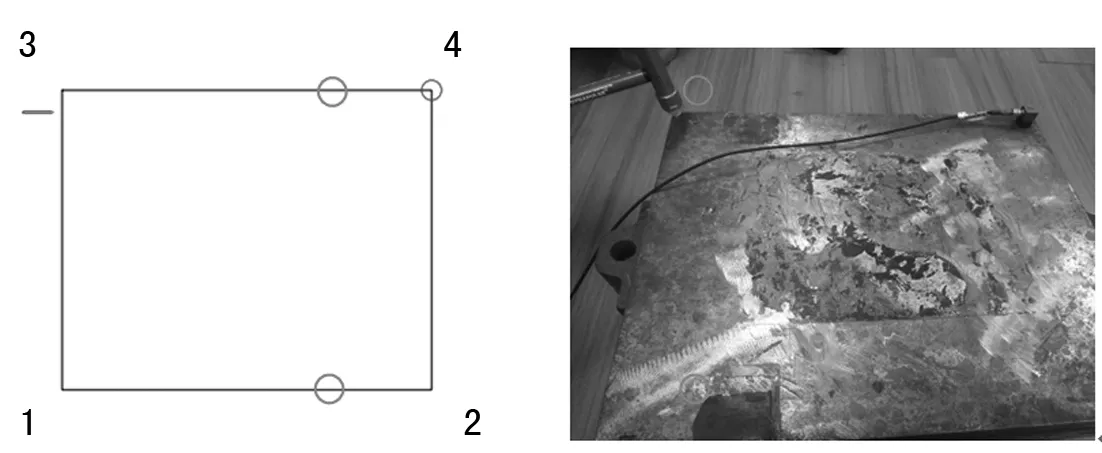
圖4 試驗測點分布

根據實測尺寸在 N-Modal模態分析軟件中建立一個 4節點的幾何模型。質量塊結構模態主要的振動方向主要體現在垂直方向，在其他方向基本沒有振動特征，因此測試主要針對結構垂直進行實驗，每個測點測試一個方向，共計4個測試自由度。

2.3 激勵信號

此次實驗質量-彈簧系統是最簡單的表現形式，采用的激勵方式為錘擊法，產生的激勵信號為脈沖信號，在基礎的模態實驗中運用比較廣泛且實用。

脈沖信號是一種離散信號，形狀多種多樣，與普通模擬信號(如正弦波)相比，波形之間在時間軸不連續(波形與波形之間有明顯的間隔)但具有一定的周期性是它的特點。激勵信號圖如圖5所示。

圖5 力錘激勵信號

2.4 互易性檢驗

對應線彈性系統，加速度響應滿足互易性，因此加速度的頻響函數也具有互易性，即i點單位激勵產生j點響應與j點單位激勵產生i點的響應相同，可表示為：

Hij(jω)=Hji(jω)

實驗過程中，取兩個個激勵點處作為互易性的校驗位置，得到的兩點間互為激勵和響應的頻響函數曲線如圖6所示。

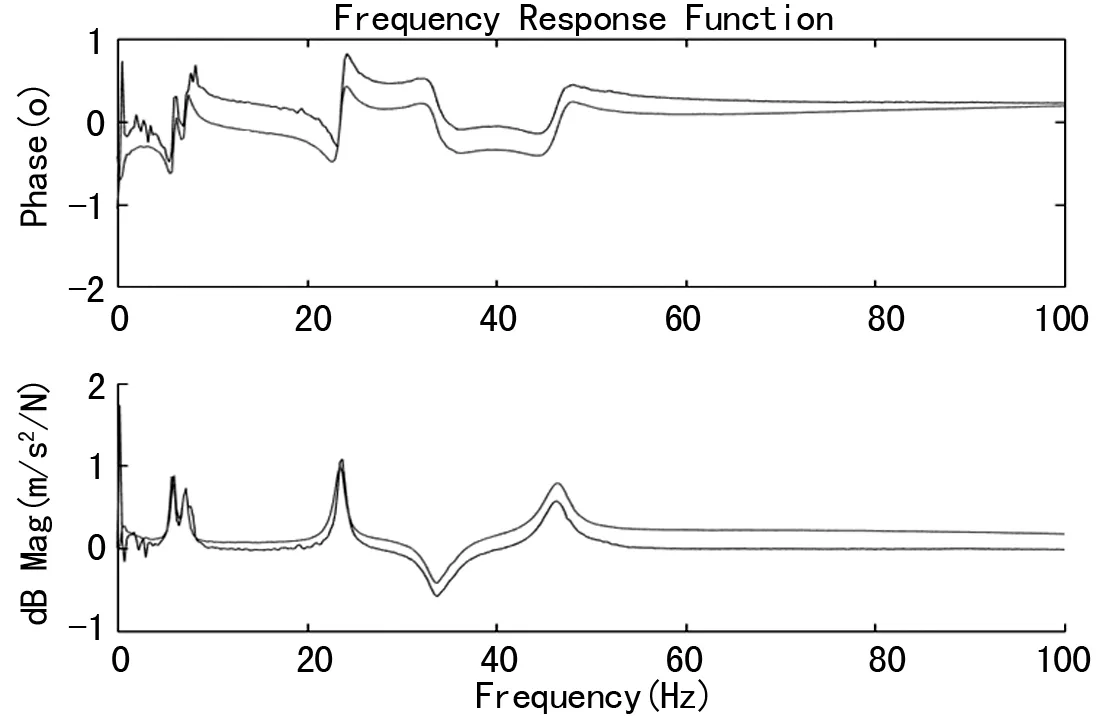
圖6 兩個激勵點間的互易性校核

從圖中可以比較清楚的看出，實驗較好的滿足了線性條件，兩條頻響函數幾乎重合，激勵設備的安裝較好的滿足條件。

3 模態識別結果對比

主要針對剛度-阻尼-質量系統垂向剛度及垂向振動阻尼系數進行分析，未對系統轉動、擺動動力學特性進行研究。由于剛體模態處于低頻段，故僅對100 Hz以內的模態頻率進行識別分析。質量塊的質量為81.45 kg時，系統垂向模態振型及頻響函數如圖7、8所示。針對不同重量的質量塊測試系統采用同樣方法進行試驗，不同質量塊狀態下模態參數識別結果如表1所列。

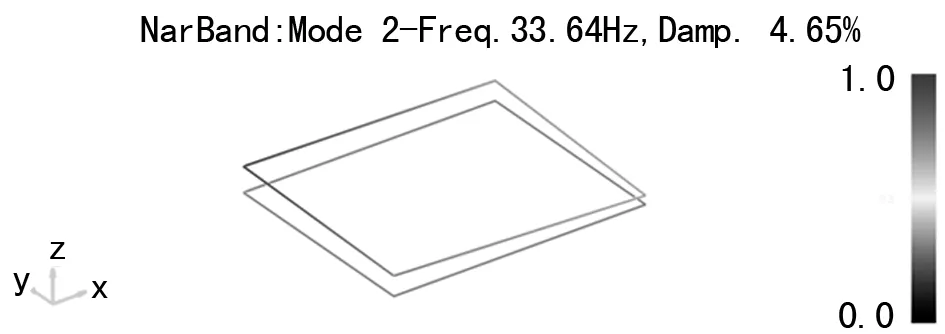
圖7 垂向振動模態振型

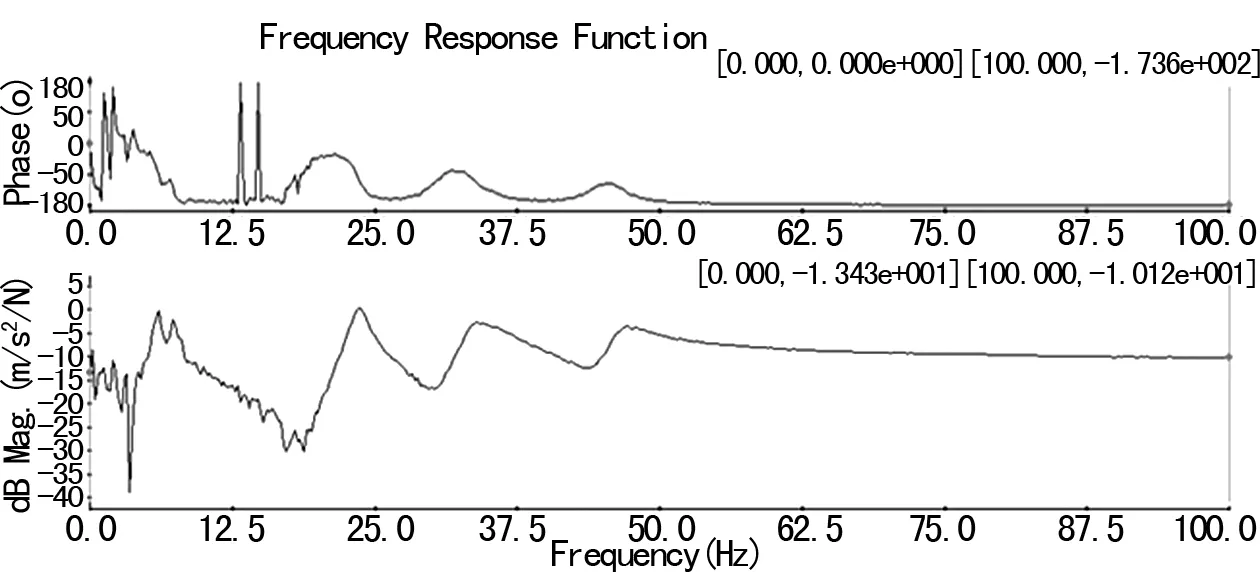
圖8 垂向振動頻響曲線

表1 模態參數識別

根據實驗及計算出的數據，得到動剛度-頻率關系擬合曲線與阻尼比-頻率關系擬合曲線，如圖9、10所示。

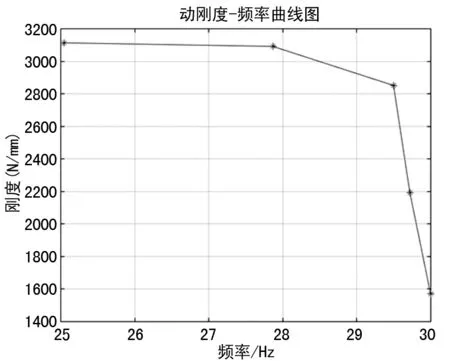
圖9 動剛度-頻率關系曲線

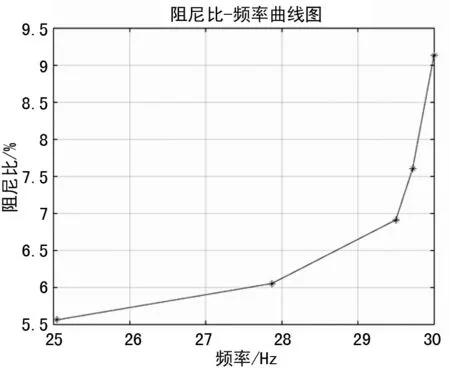
圖10 模態阻尼比-頻率關系曲線

通過對動剛度-頻率和阻尼比-頻率關系擬合曲線，可知在一定范圍內，質量-彈簧系統中彈簧的剛度隨著激勵頻率的增大而非線性減小，阻尼比隨著頻率的增大而非線性增大。

4 直接測試法測試

4.1 試驗裝置

為對比分析不同測試方法所測得的產品性能，現采用西安力創材料檢測技術有限公司生產的PL-100電伺液服疲勞試驗機進行減振件靜剛度、動剛度測試，試驗測試精度為1%，測試力值范圍0～100 kN。測試樣件、測試設備及測試安裝示意圖如圖11所示。

圖11 減振器測試樣品及測試安裝示意圖

4.2 試驗結果

文中測試方法采用TB/2843《機車車輛用橡膠彈性元件通用技術條件》中規定方法進行測試。靜剛度測試：試驗應在23 ℃±2 ℃恒溫、環境濕度為50±10%的室內進行對試樣進行加載，加載速率為3 mm/min，從零開始加載到試驗載荷上限3 kN，然后快速卸載至零，連續重復上述試驗過程三次，第三次試驗時正式記錄載荷-變形位移曲數據。動剛度測試：振幅均值0.22 mm，幅值0.11 mm，頻率6 Hz。動作次數700次，取最后20次計算動剛度值。

通過對樣品進行性能測試，測得數據如表2所列。

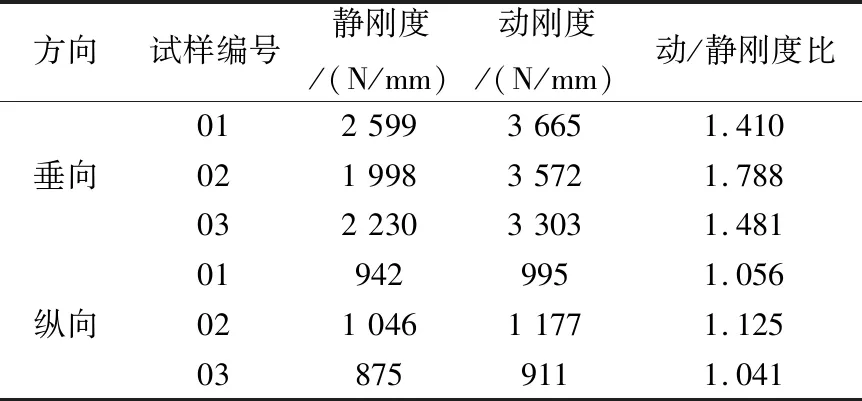
表2 減振件剛度試驗測試結果

由于減振件為回轉體，縱向與橫向剛度與阻尼值相同，故本文中僅對縱向進行測試。通過分析可知，縱向剛度僅為約為垂向剛度的1/3，垂向動/靜剛度比約為1.56，縱向動/靜剛度比約為1.07。

5 分析與結論

通過研究分析可得出以下結論：

(1) 在某共振頻率下，振動系統中模態阻尼與系統等效粘滯阻尼可實現換算。通過頻域信號的阻尼比參數識別可反向計算出系統等效粘滯阻尼，從而與減振件的產品參數實現關聯，通過此方法可實現高頻振動條件下減振件動力學參數測試。

(2) 通過模態測試法進行橡膠減振件性能參數識別所得結果與直接測試所得結果略有差異，模態測試法識別出的25 Hz低頻振動動剛度為3 112 N/mm，直接測試6 Hz振動頻率下的動剛度平均值約為3 513 N/mm，兩者數據相近，可認為模態測試法具有參考價值。

(3) 基于試驗的模態分析技術可有效實現橡膠減振件剛度、阻尼參數的識別。產品動剛度隨著頻率的增大而非線性減小，模態阻尼隨著頻率的增加而非線性增加。上海理工大學的和法家[7]就針對動剛度與振動頻率的關系做過研究，其研究表明相同振幅下，動剛度隨頻率變化趨勢呈現先增大后減小的規律，從這個層面或許可以解釋本文中產品在較高頻率范圍內呈現下降趨勢，但此次針對這一趨勢的研究與論證不夠嚴謹，還有待進一步研究。