振動篩端部預緊橫梁的有限元分析*

尚凱杰，王斌華，賀朝霞

(長安大學 道路施工技術與裝備教育部重點實驗室，陜西 西安 710064)

0 引 言

振動篩作為一種新型高效的篩分設備廣泛應用于選煤、選礦、建材、電力等行業。振動篩工況復雜，受諸多因素影響而導致篩分設備失效[1]。振動篩在工作時受到很大的交變應力，除了自身的重力、激振力以外，還會受到篩分物料的重力、下落的沖擊力以及物料隨著振動篩振動所產生的慣性力，所以實際工程運用中振動篩會出現各種故障從而使整個生產線停工停產。如果能夠對振動篩的結構特性和動態響應有所了解，則可避免停產及經濟損失，因此模態分析和諧響應分析是了解其特性的有效手段之一，既簡單高效又對設備無損。柴保明等對直線振動篩進行有限元分析得到側板危險區裂紋擴展特性、規律，以及側板疲勞壽命和安全系數；并為了提高其壽命對加強筋的布局進行了優化[2-3]。張則榮等研究得到振動篩上橫梁產生裂紋前后應變模態振型較模態頻率和位移振型有顯著變化；及應變模態變化率與橫梁損傷程度變化關系，并且預測了上橫梁疲勞損傷程度和剩余疲勞壽命[4]。李棟等對振動篩橫梁進行響應分析和疲勞分析，得到動力響應情況，估算其壽命周期[5]。邵堃等研究圓振動篩篩體得出篩箱焊接后的變形量及殘余應力分布[6]。張青召等研究了大型振動篩在啟動過程中的運動規律[7-8]。前學者們的研究集合了振動篩大部分失效形式以及如何進行分析、結構改進，為以后的振動篩設計分析提供了寶貴的經驗。目前，針對振動篩模型基本都是以實體單元為主，而筆者以板殼單元為主，再結合振動篩實際斷裂位置建立局部實體模型進行計算。現以某型振動篩為例，復雜的受力導致振動篩的端部預緊橫梁出現斷裂，為了探究振動篩開裂原因，建立有限元模型，進行模態分析、諧響應分析，分析在給定激振工況下的受力，對其合理性進行評價。

1 振動篩簡述

振動篩為雙振動電機驅動，主要由篩箱、篩網、電機、阻尼彈簧、支撐管梁等組成。振動篩除了要承受自身的重力、激振力外，還會受到物料的重力、下落沖擊力、物料隨振動篩產生的慣性力及振動篩工作時產生的交變應力等，復雜的受力易導致振動篩產生結構破壞。振動篩篩體的主要材料Q235A，材料密度7 850 kg/m3，泊松比0.3，彈性模量E=210 GPa，材料許用應力157 MPa；振動篩的主要結構參數：激振頻率16.7Hz，振動方向角58°，篩面傾角11°。

2 有限元模型的建立

2.1 單元選擇

振動篩可以看作是空間板梁組合結構，因此采用ANSYS中殼單元SHELL181進行板結構的模擬；兩個側板之間以及篩網模擬采用BEAM188單元，篩網與橫梁通過主從節點建立耦合達到力的傳遞；采用質量單元MASS21模擬物料及偏心輪質量；彈簧-阻尼單元采用COMBIN14單元進行模擬，將彈簧上節點與彈簧支座建立剛性區域達到力的傳遞。

2.2 物料模擬

采用MASS21單元模擬物料質量，將物料平均分配到振動篩的五層篩網上，物料與橫梁建立Y向耦合以達到重力傳遞，篩分率為95%，物料粒徑與占比如表1所列。

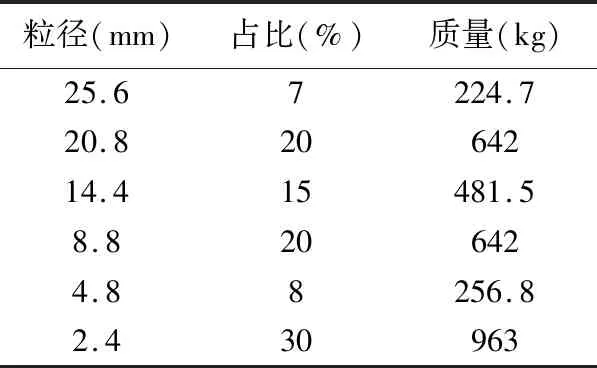
表1 物料粒徑與占比

2.3 激振力模擬

使用MASS21單元模擬偏心塊質量，將兩個質點與電機橫梁對應螺栓位置進行耦合建立剛性區域以達到激振力的傳遞。電機激振力為2×245 kN，靜扭矩2×2 236 kg·mm。由已知振動方向角58°，篩面傾角11°，激振力有效傳遞90%，為在ANSYS中方便施加激振力，將激振力分解為X向與Y向分力，兩分力分別為：

X方向分力：

Fx=Fcos 58°×90%

=245 000×cos 58°×90%≈116 847 N

(1)

Y方向分力：

Fy=Fsin 58°×90%

=245 000×sin 58°×90%≈186 995 N

(2)

2.4 支撐彈簧模擬

根據振動篩實際工況，在彈簧支座處建立彈簧單元，縱向彈簧模擬實際彈簧豎向剛度。由于振動篩在電機產生的激振力作用下會產生軸向與橫向的振動，因此利用COMBIN14單元模擬彈簧時，增加橫向彈簧來模擬實際彈簧的橫向剛度。

綜上：可得振動篩有限元模型如圖1、2所示。

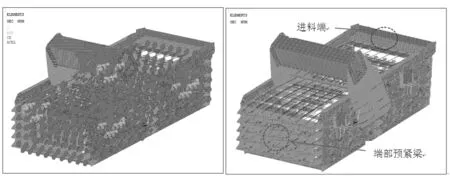
圖1 振動篩有限元模型(含邊界條件) 圖2 振動篩有限元模型(不含邊界條件)

3 有限元模型模態分析

模態分析是動力學分析基礎，模態分析可以確定結構的固有頻率和振型。設置最大提取模態階數為10，采用分塊Lanczos法提取振動篩的模態頻率和振型等模態參數[9]。對于一般結構，要求各階固有頻率要遠離工作頻率，具體是要求工作頻率不落在某階固有頻率的半功率帶寬內；對結構振動貢獻較大的振型不影響其正常工作[10]。模態頻率結果如表2所列。第7、8階模態振型分別如圖3、4所示。

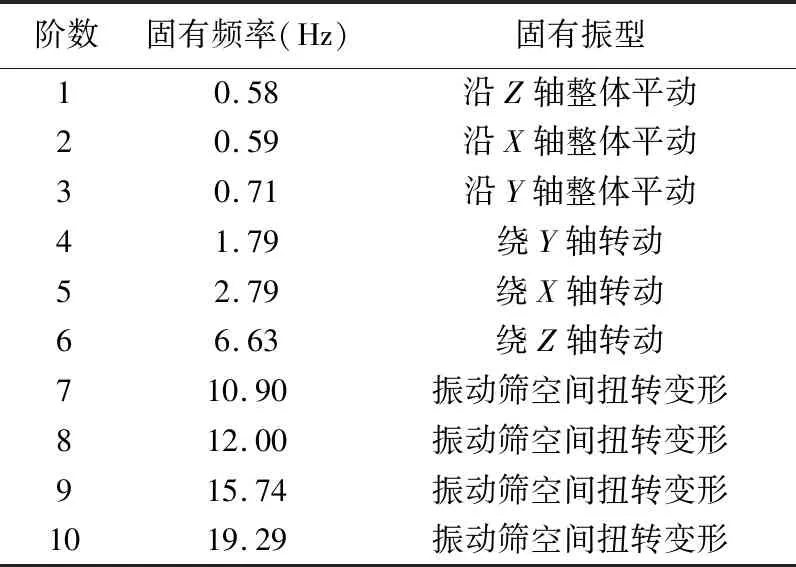
表2 模態頻率結果

圖3 振動篩第7階模態振型圖 圖4 振動篩第8階模態振型圖

由表2可知，前6階模態為剛體的平動與轉動，其余模態振型為彈性變形。第7階模態頻率為10.93 Hz，第12階模態頻率為19.37 Hz，對應振型為空間扭動，而振動篩的工作頻率為16.7 Hz，遠離其固有頻率，說明振動篩模態頻率分布合理。

4 振動篩出口端梁諧響應分析

振動篩在工作時由電機帶動激振器產生交變激振力，振動篩橫梁、篩框、激振器橫梁都會產生動應力，為了進一步了解動應力數值及分布規律，需對振動篩進行諧響應分析。考慮實際斷裂位置，選擇出口端的預緊力橫梁為主要分析對象。

4.1 預緊端梁啟動階段應力分析

設置分析頻率為0～100 Hz，采用完全法對振動篩進行諧響應分析。由實際振動篩預緊力梁斷裂位置選出五根橫梁中的第二根橫梁，由于有限元模型節點眾多，選出斷裂位置具有代表性的節點編號797 542，查看其應力-頻率圖如圖5所示。由第一主應力的應力幅-頻譜圖可知：振動篩在頻率0.7 Hz與6.6 Hz時均出現高應力峰值，說明在實際工作過程中，振動篩電機啟停時會出現瞬時高應力狀態，讀取預緊力橫梁二在Freq=0.7 Hz和Freq=6.6 Hz時的S1應力云圖如圖6、7所示。由此可知振動篩在電機啟停過程出現的瞬時大應力會導致結構易出現斷裂，這也與實際斷裂位置相符，說明該分析方法合理，可用于指導產品改進。

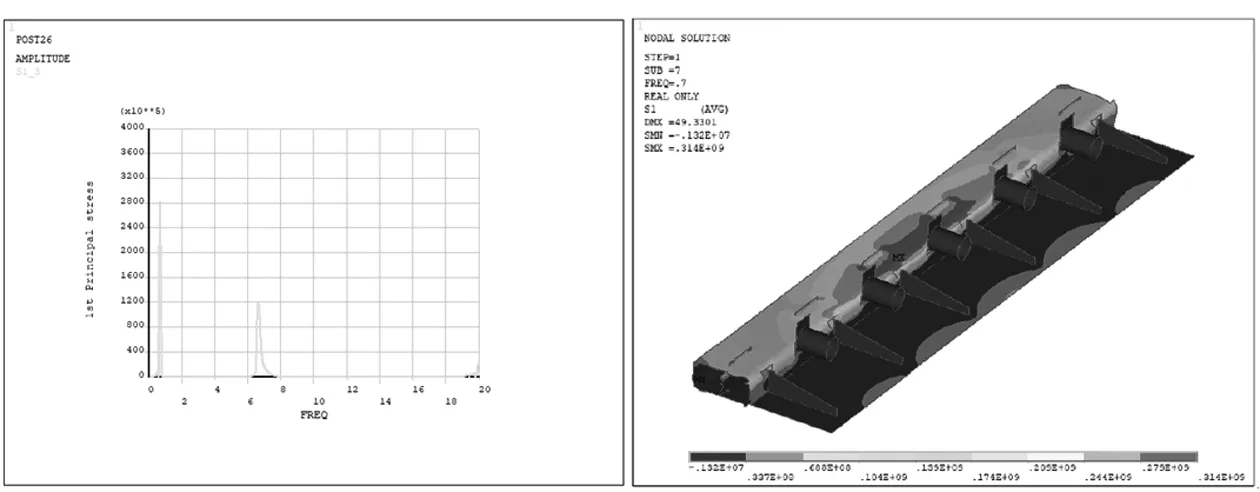
圖5 橫梁二跨中位置焊接處S1應力幅-頻譜圖 圖6 橫梁二Freq=0.7 HzS1應力云圖

圖7 橫梁二Freq=6.6 HzS1應力云圖 圖8 Freq=16.7預緊梁S1應力云圖

4.2 預緊端梁工作頻率段應力分析

圖8為振動篩預緊力橫梁在工作頻率16.7 Hz下的等效應力分布云圖。由圖12可以看出預緊力梁最大應力位置出現在梁的兩端，最大應力值為32.7 MPa，其余位置應力均比較小，都低于材料許用應力，說明振動篩在工作狀態下滿足要求。

5 振動篩焊縫區精細有限元分析

為了精確分析危險構造細節的應力狀態，將關鍵構造細節轉換成實體模型結構進行精細分析。采用實體單元SOLID186單元模擬，并根據實際焊接加工圖建立焊縫構造，實體單元與板殼單元的連接采用接觸單元，設置MPC(即多點約束方程)算法，通過MPC可將SHELL單元與SOLID單元進行連接計算,MPC不需要連接處節點一一對應便可將不連續、自由度不協調的單元連接，本質為設置接觸單元的接觸算法為MPC algorithm，并定義接觸面行為綁定來實現。實體單元模型如圖9所示，實體單元與板殼元連接如圖10、11所示。

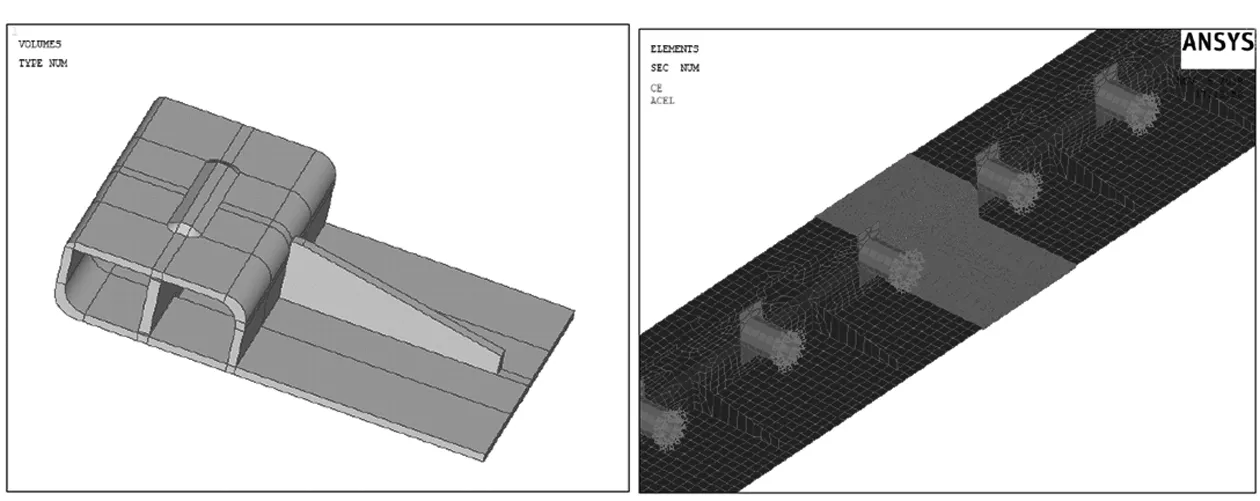
圖9 實體單元模型圖 圖10 實體單元與板殼元連接

通過諧響應分析計算，得出實體模型段焊縫區域第一主應力的應力幅-頻譜圖，選擇代表節點938 624和938 636，如圖12所示。由圖可知振動篩在Freq=0.7 Hz與Freq=6.7 Hz時出現高應力峰值，獲得其對應頻率的應力云圖如圖13、14所示。

圖11 局部實體單元與板殼元連接圖 圖12 焊縫區域S1應力幅-頻譜圖

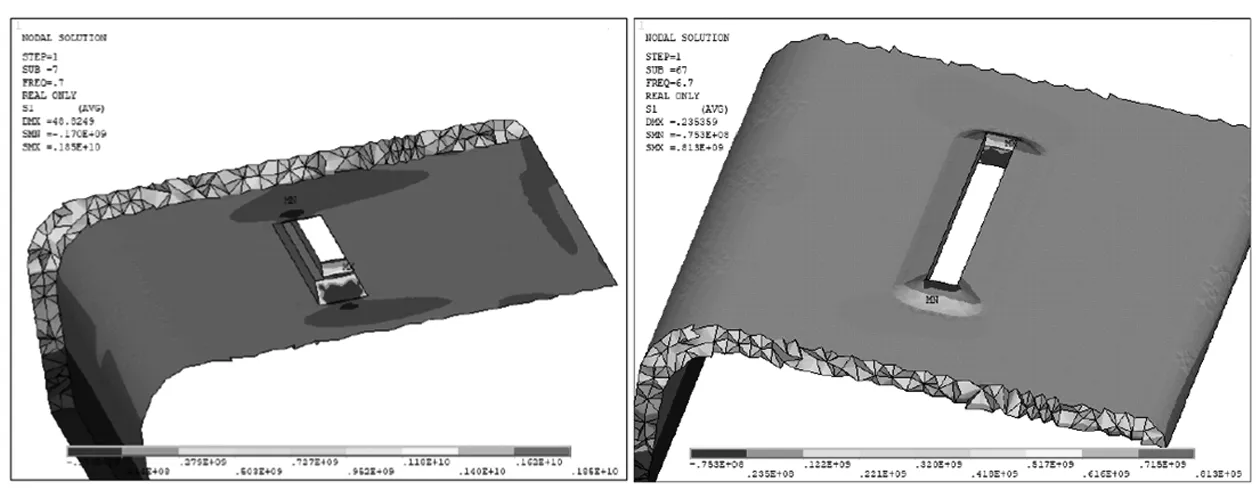
圖13 上表面焊縫區域應力云圖Freq=0.7 Hz 圖14 上表面焊縫區域應力云圖Freq=6.7 Hz

由此可知振動篩在低頻時橫梁跨中段出現應力集中，頻率為0.7 Hz時最大應力集中1 850 MPa，頻率為6.7 Hz時最大應力集中813 MPa，假定材料的彈性變形沒有考慮材料的塑性屈服，因此應力值只反映應力集中程度，并不代表真實應力值，該應力值明顯大于材料屈服強度，因此應力集中明顯，設備啟停過程中易發生瞬時應力峰值導致裂紋萌生，說明實際結構此處容易出現斷裂[11-12]。

6 結 論

以某公司設計的振動篩為例，結合振動篩實際工況建立了有限元模型，并進行了模態分析及諧響應分析，最終得出以下結論：

(1) 振動篩整體結構模態分析結果表明，振動篩固有頻率避開了工作頻率16.7 Hz，正常運行階段不會出現共振現象。

(2) 振動篩的諧響應曲線以及應力結果表明，振動篩預緊力橫梁大應力的發生頻率出現在0.7 Hz及6.7 Hz附近，表明振動篩含料每次啟動或者停止過程中會出現極大的瞬時應力，導致結構裂紋萌生和擴展。

通過對振動篩進行三維建模、有限元分析得出振動篩設備端部預緊橫梁開裂原因，對振動篩結構改進具有參考意義。但振動篩工作時可能會有些非線性狀況，而諧響應適用于規律變量，具有局限性，所以在非線性方面要做更加深入的研究來彌補諧響應分析的不足，進而更好的將理論應用于實際。