旋轉載體圓錐姿態解算方法研究*

張雙彪，李興城

(1 北京信息科技大學高動態導航技術北京市重點實驗室, 北京 100101; 2 北京理工大學宇航學院, 北京 100081)

0 引言

火箭彈、制導炮彈、制導子彈等旋轉載體常采用的姿態解算方法是以歐拉角為基礎的，如歐拉角姿態解算方法和基于旋轉矢量的雙步姿態解算方法，前者常用于控制系統設計，后者常用于定位、定向和導航系統，但兩種方法均受錐形運動影響而出現不同程度的姿態解算誤差[1-2]，因此姿態解算得到了國內外廣大學者的關注。研究發現，旋轉載體的錐形運動存在兩種旋轉方式，一種是通過繞3個正交軸旋轉表征的形式，如圖1所示；另一種是載體因定軸轉動而發生的章動和進動表現的雙軸旋轉形式，如圖2所示[3-4]。兩種錐形運動均會影響姿態解算方法，特別是自轉姿態誤差發散嚴重。為提高姿態解算的適應性和解算精度，廣大學者主要采用便于參數優化的雙步姿態解算方法，通過錐形運動條件優化旋轉矢量的計算參數，抑制姿態誤差，并利用旋轉矢量計算姿態矩陣，得到載體姿態，而優化效果憑借誤差漂移率體現[5-9]。然而，目前該類姿態誤差并未得到有效消除。

圖1 三軸旋轉表征的錐形運動

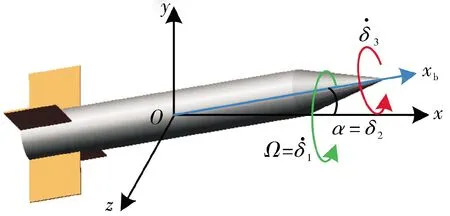
圖2 兩軸旋轉表征的錐形運動

為此，提出圓錐姿態解算方法，并給出基于旋轉矢量的雙步姿態解算過程，通過與傳統的解算方法進行仿真對比，證明該方法的優越性。

1 常規的姿態解算方法

1.1 歐拉角姿態解算方法

歐拉角姿態解算方法是傳統的姿態解算方法，根據飛行力學知識，載體的角運動模型為[10]：

(1)

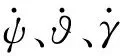
(2)

利用獲得的角速度測量值，可以解算載體姿態。由歐拉角表示的載體坐標系Oxbybzb到參考坐標系Oxyz的姿態矩陣為：

(3)

式中:上角標i表示目標坐標系為參考坐標系;C11=cos(?)cos(ψ)；C12=-sin(?)cos(ψ)cos(γ)+sin(ψ)sin(γ)；C13=sin(?)cos(ψ)sin(γ)+sin(ψ)·cos(γ)；C21=sin(?)；C22=cos(?)cos(γ)；C23=-cos(?)sin(γ)；C31=-cos(?)sin(ψ)；C32=sin(?)sin(ψ)cos(γ)+cos(ψ)sin(γ)；C33=-sin(?)·sin(ψ)sin(γ)+cos(ψ)cos(γ)。

在錐形運動環境下，利用俯仰角?和偏航角ψ可以近似計算半錐角：

(4)

1.2 雙步姿態解算方法

雙步姿態解算方法包括旋轉矢量更新和姿態矩陣更新兩個過程，具體更新如下[3]：

φl=αl+δφl

(5)

(6)

(7)

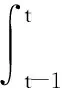
式中l表示第幾次循環，為便于數據更新，式(7)常被近似為下式：

(8)

式中kij為旋轉矢量優化參數。

姿態矩陣更新如下：

(9)

(10)

(11)

(12)

(13)

利用旋轉矢量解算歐拉角時，俯仰角?、偏航角ψ和滾轉角γ分別利用下式計算：

(14)

(15)

(16)

偏航角ψ和滾轉角γ真值根據表1和表2確定。

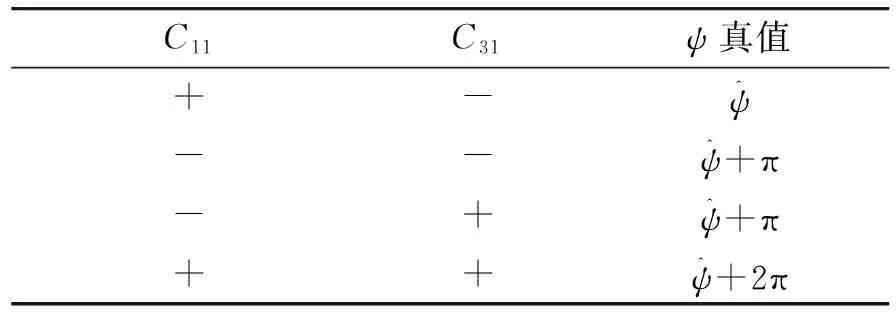
表1 ψ取值

2 圓錐姿態解算方法

圓錐姿態解算方法借鑒了章動原理，通過定義圓錐姿態角表述錐形運動，分別為進動角δ1，章動角δ2，自轉角δ3，其中δ1取值范圍為[0° 360°]，δ2取值范圍為[0° 90°]，δ3取值范圍為[0° 360°][8]。進動角表征錐形運動的旋轉過程，章動角表征錐形運動的搖擺幅度，自轉角則表征載體在進行錐形運動時自轉過程，見圖2。需要說明的是，當Oxbyb面位于鉛垂面內時為進動角δ1起始位置。與章動原理不同的是，文中針對坐標系旋轉過程進行了改進，具體為：

根據旋轉順序可以得到通過圓錐姿態角表示的參考坐標系Oxyz與載體坐標系Oxbybzb的旋轉關系，如圖3所示。

圖3 錐形運動姿態角的兩軸旋轉過程

根據圖3建立旋轉載體的角運動方程為：

(17)

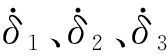
(18)

當δ2不為零時，根據式(18)可以利用角速度測量值實時解算錐形運動的姿態角。根據歐拉姿態角與圓錐姿態角的幾何關系建立如下表達式：

?=±arcsin|sinδ1sinδ2|

(19)

(20)

二者的符號可以根據表3和表4選取。

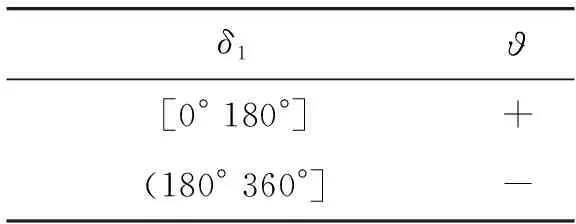
表3 ?符號選取

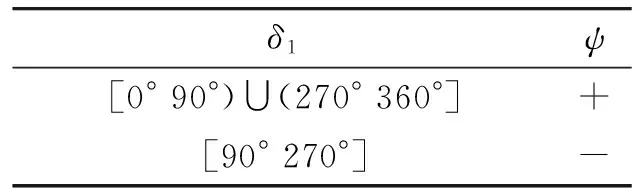
表4 ψ符號選取

由式(18)可知，當δ2為零時，存在奇異值的問題。為提高圓錐姿態適應性，同樣可以利用雙步姿態解算結構更新載體的圓錐姿態，見式(5)～式(10)，載體坐標系Oxbybzb到參考坐標系Oxyz的圓錐姿態矩陣可根據圖3旋轉關系確定，具體為：

(21)

式中:D11=cosδ2；D12=-cos(δ1-δ3)sinδ2；D13=-sin(δ1-δ3)sinδ2；D21=cosδ1sinδ2；D22=sin(δ1-δ3)sinδ1+cos(δ1-δ3)cosδ1cosδ2；D23=-cos(δ1-δ3)sinδ1+sin(δ1-δ3)cosδ1cosδ2;D31=sinδ1sinδ2；D32=-sin(δ1-δ3)cosδ1+cos(δ1-δ3)sinδ1cosδ2；D33=cos(δ1-δ3)cosδ1+sin(δ1-δ3)sinδ1cosδ2。

根據式(21)，可以建立圓錐姿態計算公式：

(22)

δ2=arccosD11

(23)

(24)

需要說明的是，自轉角δ3是需要確定進動角δ1后再計算。進動角δ1和自轉角δ3的真值可根據表5和表6所示確定。

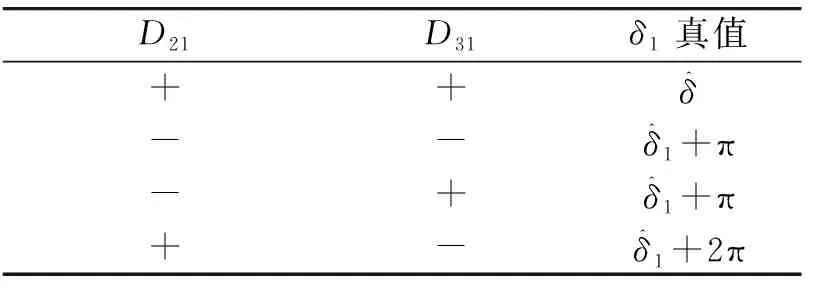
表5 δ1取值

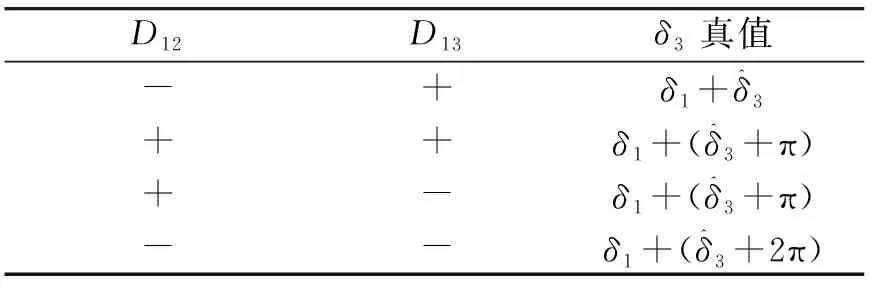
表6 δ3取值

3 仿真與分析

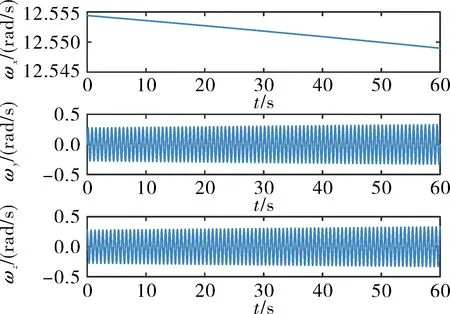
圖4 角速度測量值

首先，將歐拉角姿態解算方法與雙步姿態解算方法進行對比。圖5為旋轉矢量方法優化后歐拉角姿態誤差，姿態角存在振蕩式發散誤差，誤差量級為10-5～10-4rad。圖6為旋轉矢量方法優化前后的歐拉角姿態誤差對比，誤差表現為復雜的發散現象，量級為10-14～10-13rad。結合圖5和圖6，說明雙軸旋轉錐形運動引起的姿態發散振蕩誤差，在旋轉矢量優化后仍然存在，優化效果并不明顯，同時說明利用雙步姿態解算方法得到歐拉角存在誤差。

圖5 旋轉矢量方法優化后歐拉角姿態誤差

圖6 旋轉矢量方法優化前后的歐拉角姿態誤差對比

然后，將圓錐姿態解算方法與雙步姿態解算方法進行對比。圖7為旋轉矢量方法優化后圓錐姿態誤差，可見仍存在振蕩式誤差，但并未發散，章動角δ2誤差量級為10-5rad，自轉角δ3的誤差量級為10-6rad，精度均高于歐拉角姿態。圖8為旋轉矢量方法優化前后圓錐姿態誤差對比，優化前后誤差并未發散，誤差量級為10-4～10-3rad，且自轉角δ3精度未得到提高。分析圖7和圖8可知，旋轉矢量方法的優化與否對圓錐姿態自轉角的影響并不明顯，同時也證明雙步姿態解算方法存在誤差。

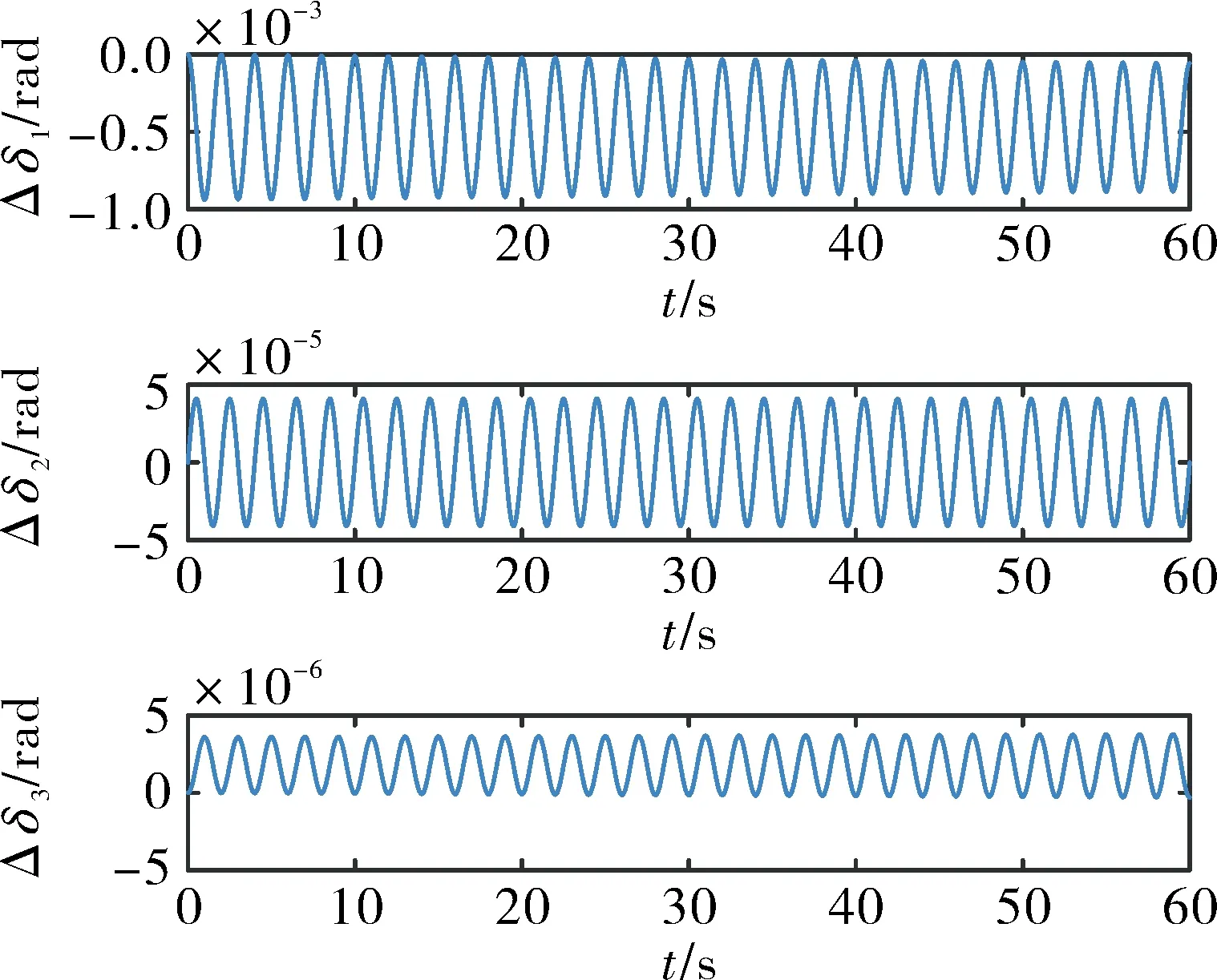
圖7 圓錐姿態解算方法與旋轉矢量對比

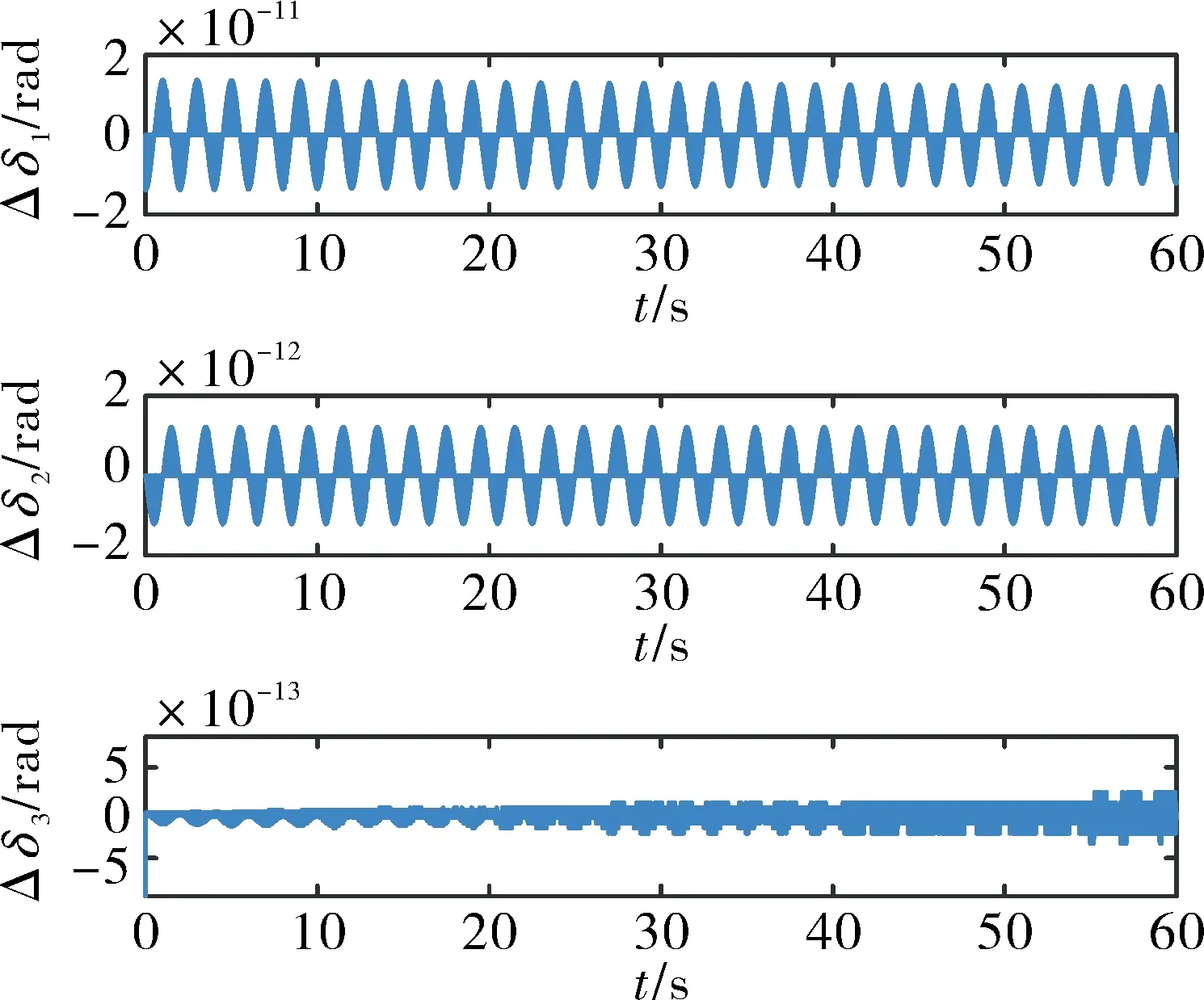
圖8 旋轉矢量方法優化前后的圓錐姿態誤差對比

最后，分別利用基于歐拉角姿態的解算方法與基于圓錐姿態的解算方法計算半錐角α，并進行對比。如圖9所示，歐拉角姿態計算存在發散的誤差，圓錐姿態解算方法無誤差，但其雙步姿態解算方法存在不發散的振蕩誤差，具體誤差關系為：

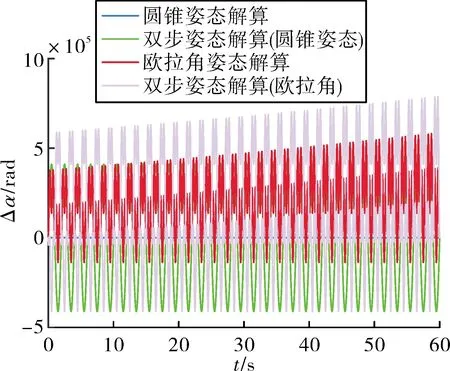
圖9 半錐角誤差

Δα圓錐姿態解算<Δα歐拉角姿態解算<Δα雙步(圓錐姿態)<Δα雙步(歐拉角)

4 結論

考慮了錐形運動存在的不同形式，提出了一種圓錐姿態解算方法，同時為提高該方法的適應性，給出了基于旋轉矢量的解算過程，通過與傳統姿態解算方法對比發現：

1)相比傳統方法，圓錐姿態解算方法的精度高于歐拉角姿態解算方法。

2)基于雙步姿態解算的圓錐姿態解算精度高于基于雙步姿態解算的歐拉角姿態解算，且常規優化的旋轉矢量方法效果并不明顯。

文中提出的圓錐姿態解算方法更適合旋轉載體的雙軸錐形運動條件，能夠為旋轉載體的復雜角運動解耦和姿態誘導誤差抑制的研究工作提供理論參考。未來工作將進一步研究雙步姿態解算方法引起姿態出現發散的振蕩誤差的機理，以及相應的誤差抑制方法。