節理巖體對SV波傳播的影響

路世偉，劉洪宇，孫金山，周傳波

(1.長江大學城市建設學院，湖北 荊州 434023；2. 江漢大學湖北(武漢)爆炸與爆破技術研究院，武漢 430056；3.中國地質大學工程學院，武漢 430074)

天然的節理巖體并不是均質體，而是由許多的不連續面組成的。這其中包括斷層、節理、裂隙等，這就造成了天然節理巖體不同的各項指標，對節理巖體的不均勻性和不連續性都有著很大的影響。

國內外許多學者從理論和試驗兩方面對節理面對應力波傳播影響進行了深入的研究。在計算中，平面節理巖體中的SV波是應用最普遍的應力波，影響很大，所以研究SV波在節理面上的傳播有很重要的意義。孫金山等[1]運用數值模擬的方法分析了爆破地震波中P波對鄰近圓形隧道動力擾動特征。趙堅等[2]則用 UDEC 模擬了爆炸波在節理巖體中的傳播。張艷玲等[3]利用LS-DYNA有限元分析軟件,通過三維數值模擬,分別從振速、能量和強度等方面研究節理對爆破應力波傳播的影響。薛小蒙等[4]利用ANSYS數值軟件,研究了不同厚度、角度和充填材料的結構面對應力波的影響規律。也有許多學者[5-6]對應力波在不同工況下的傳播及影響進行了研究。王衛華等[7]、林發榮等[8]、丁梧秀等[9]對節理單元對波的影響及其穩定性進行了分析。林建生等[10]、許建聰等[11]、簡文彬等[12]、章在墉等[13]、胡鈞等[14]對波在不同地區的傳播進行了分析。

在解決巖體及巖石動力學的防護問題上，節理對波能量的衰減成為了人們最關心的問題之一。研究這一問題可以提高工程實踐中波對工程影響的準確度和可靠性，且對巖石動力學、防災減災工程等學科具有基礎性意義。

1 計算模型

為簡化計算，選擇含2條平行節理的節理巖體為研究對象，建立尺寸為36 m×12 m的平面應變問題數值模型(見圖1)，節理傾角α=90°，巖體的體積模量為6.36 GPa，剪切模量為1.36 GPa，密度取值為2 650 kg/m3，入射波頻率為50 Hz。設節理間距為d，監測點間距為d/5。在節理1前、節理間以及節理2后共布置了6個監測點(見圖2)。

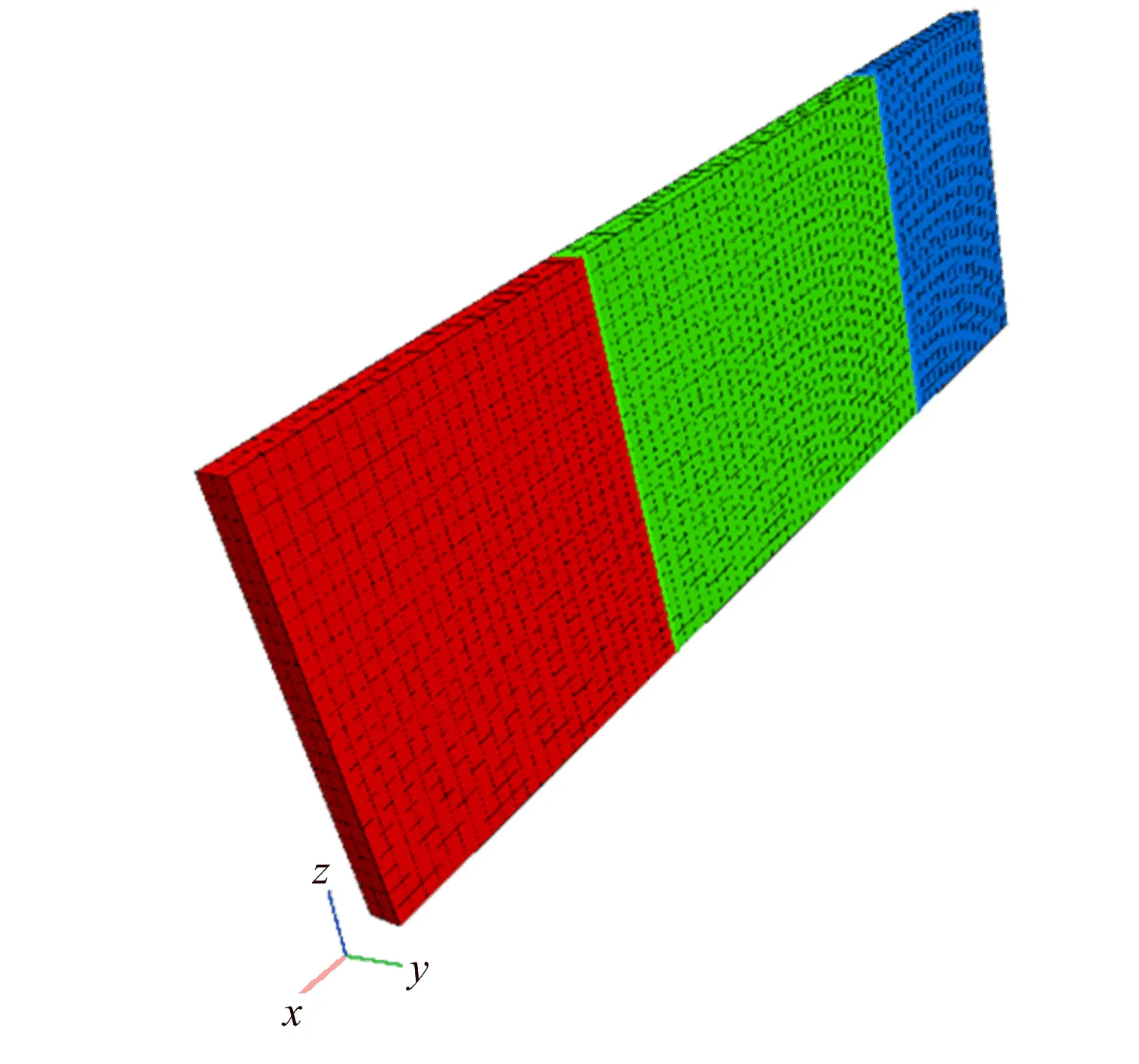
圖1 雙平行節理巖體數值模型Fig.1 Numerical model of rockmass with two parallel joints

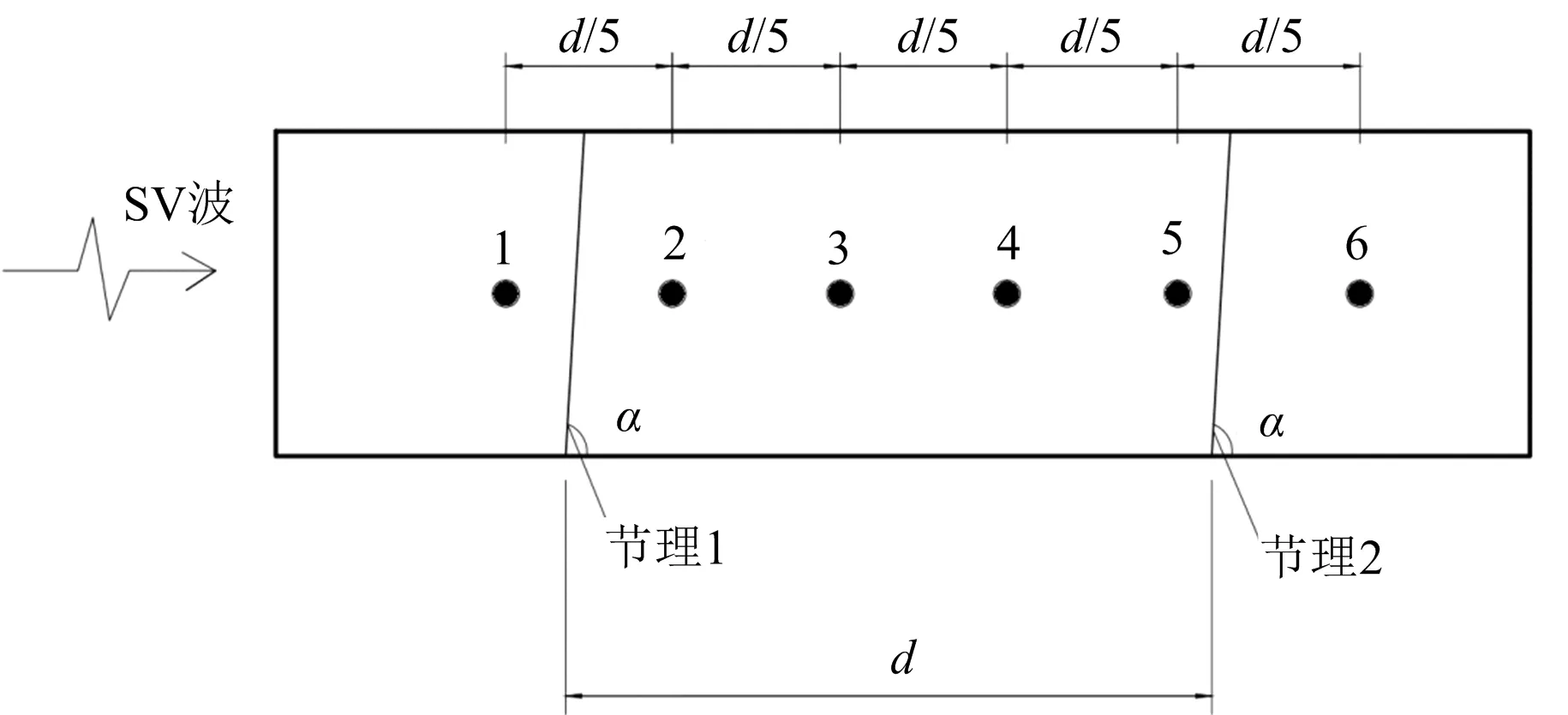
注：1～6為監測點編號圖2 監測點布置Fig.2 Layout of monitoring points

2 模型可靠性驗證

為驗證數值計算結果的可靠性，選擇單節理模型計算結果與理論分析結果進行對比，通過FLAC3D數值模擬軟件建立單節理巖體數值模型(見圖3)。當SV波垂直入射時，反射系數和透射系數理論計算公式[15]分別為

(1)

圖3 單節理巖體數值模型Fig.3 Numerical model of rockmass with a single joint

不同節理剛度情況下透射系數和反射系數的大小變化情況如圖4所示，當0.5≤K<3.0時，透射系數會逐漸增大；當K≥3.0時，透射系數趨于1，相當于SV波的全部透射，但是在節理巖體中發生反射的概率相當小，趨近于0。相反，反射系數逐漸減小，在K≥3.0時趨近于0，與理論計算結果基本上吻合。由以上分析可知，FLAC3D的模擬結果能夠準確地反映平面SV波在節理巖體中的傳播規律，利用基于FLAC3D數值模擬軟件研究平面SV波在節理巖體中的傳播規律的研究是可行的。

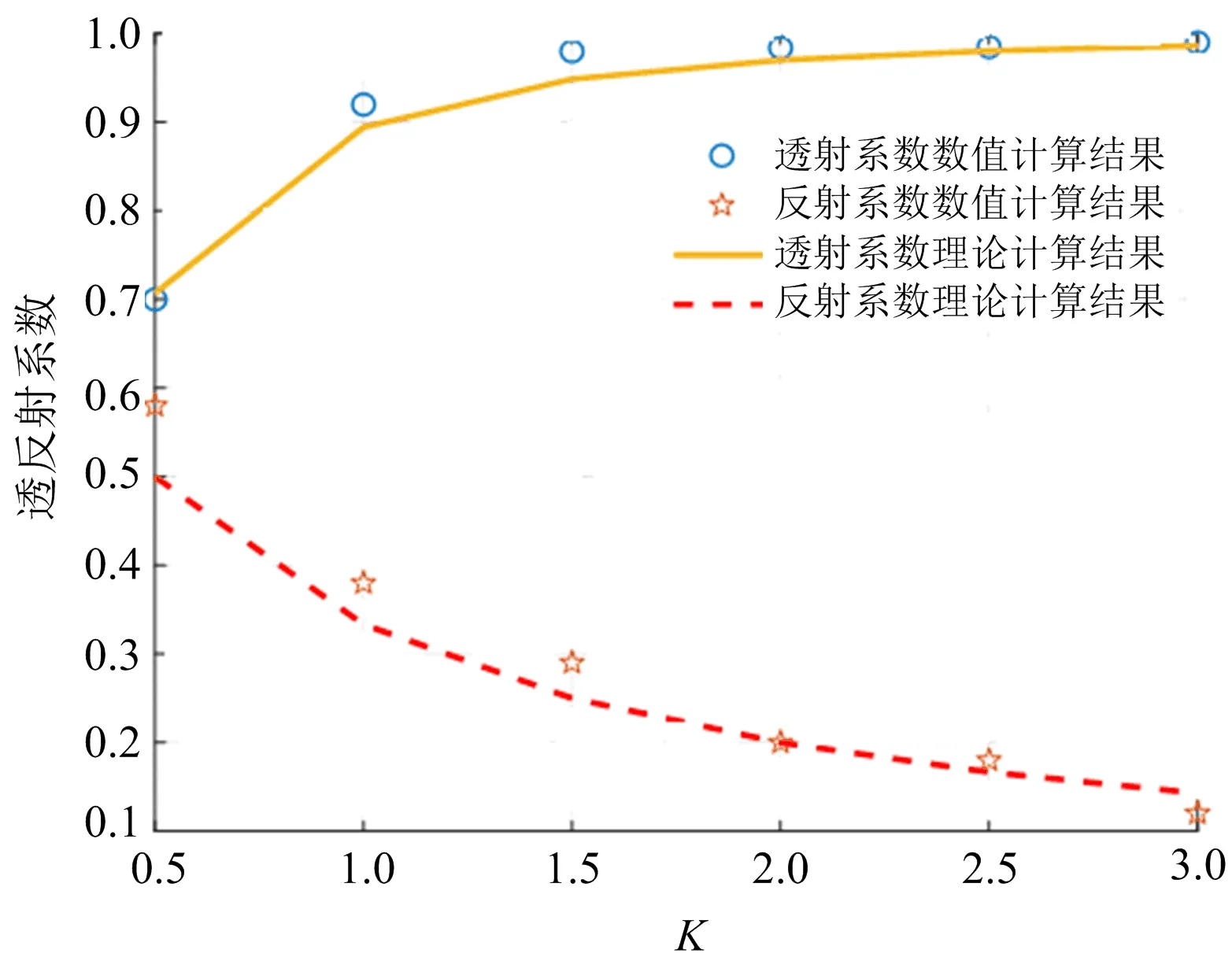
圖4 不同節理剛度下透射系數和反射系數變化情況Fig.4 Variation of transmission coefficient and reflection coefficient under different joint stiffness

3 結果與討論

由于在線彈性動力學中，各監測點質點振動速度線性地依賴于入射波的質點振動速度，即各監測點質點振動速度是入射波質點振動速度的線性齊次函數，因而研究各監測點質點振動速度與入射波質點振動速度的比值更具有一般性價值，為得出一般性的結論，需要定義如下參數：

質點振動速度放縮系數的定義為

(2)

式中：v(n)(t)為編號n點的振動速度；v(i)(t)為入射波的振動速度。

等效節理剛度的定義為

(3)

式中：Kn、Ks分別為節理法向、切向剛度；ω為入射波的角頻率;Zp為波阻抗，且Zp=ρCp，ρ為巖體密度，Cp為巖體縱波波速。

3.1 節理剛度下SV波的傳播規律

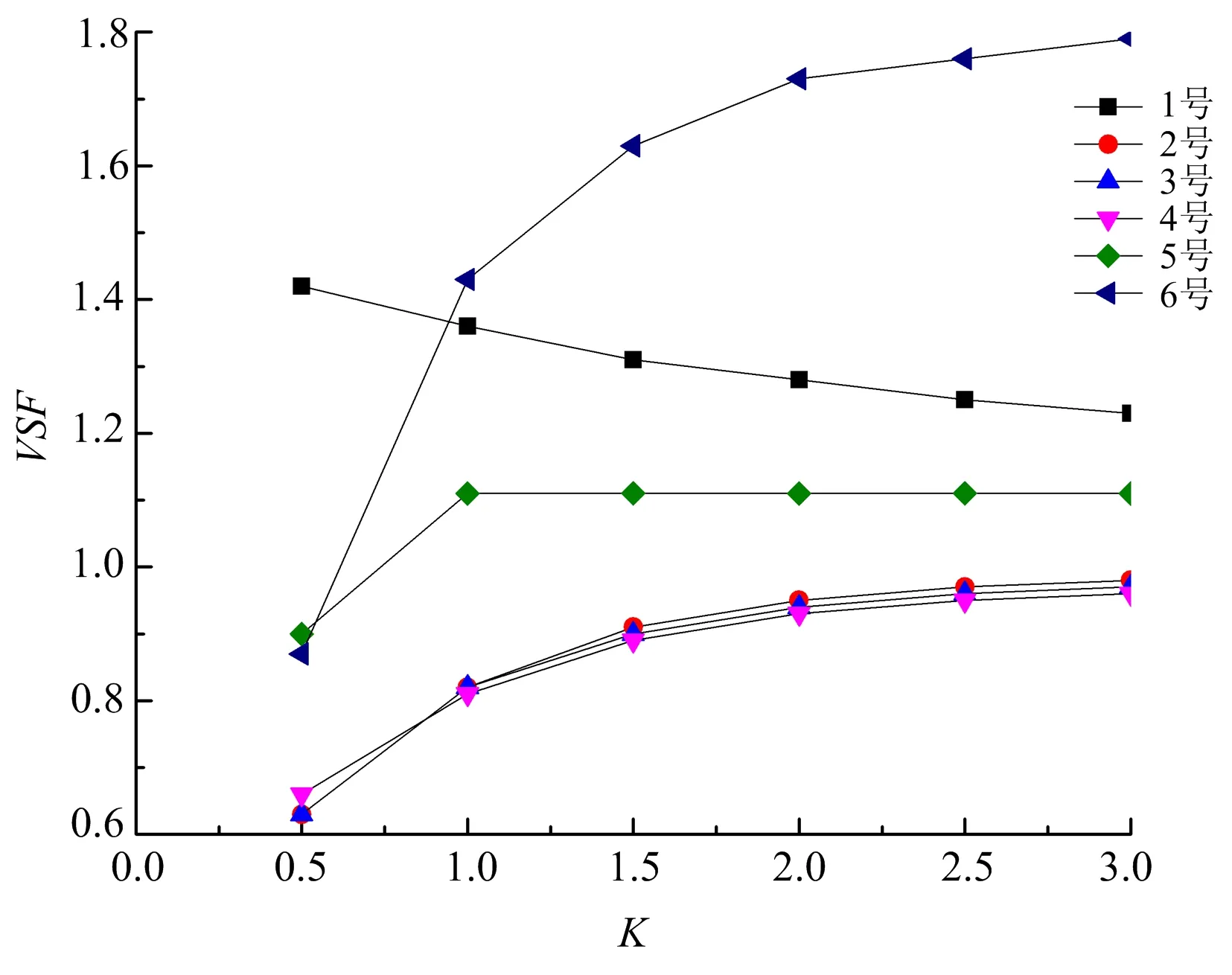
圖5 各監測點VSF隨節理剛度變化關系Fig.5 The relationship between the VSF of each monitring point and the joint stiffness

由圖5可知，1號監測點的VSF隨著等效節理剛度K的增大而逐漸減小，逐漸趨向1.2；2號、3號、4號監測點的VSF隨著K的增大而增大，且其幅值及變化規律非常接近。在K相同的情況下，當K=0.5時，越靠近節理1，VSF越小，而當K增大時，VSF表現出相反的變化特性。5號監測點的VSF也隨著K的增大而增大，但K>1.0時，VSF的值基本保持不變的。6號監測點的VSF也隨著K的增大而增大，當K≤1.0時,VSF增大速度較快，當1.0≤K≤2.5時,VSF增大速度逐漸減小，當K>2.5時,VSF變化較小且趨向于1.8。

由以上分析可知，等效節理剛度K對不同位置的VSF的影響并不相同。總體來說，對節理1前的質點而言，VSF隨K的增大而逐漸減小，而對于節理間以及節理2后的質點而言，VSF隨K的增大而逐漸增大，但不同位置的VSF值及其增大速度并不相同。

3.2 節理傾角對SV波傳播的影響

為了研究節理傾角對SV波傳播的影響，選擇相同節理剛度的條件來分析節理傾角對其產生的影響，因此取兩種剛度K作為分析，其值分別取0.5和3.0。分別對兩種剛度條件下的5種節理傾角進行分析(α取30°、40°、45°、50°、60°)。

各監測點的質點峰值振動速度放縮系數隨節理傾角變化關系如圖6～圖7所示。

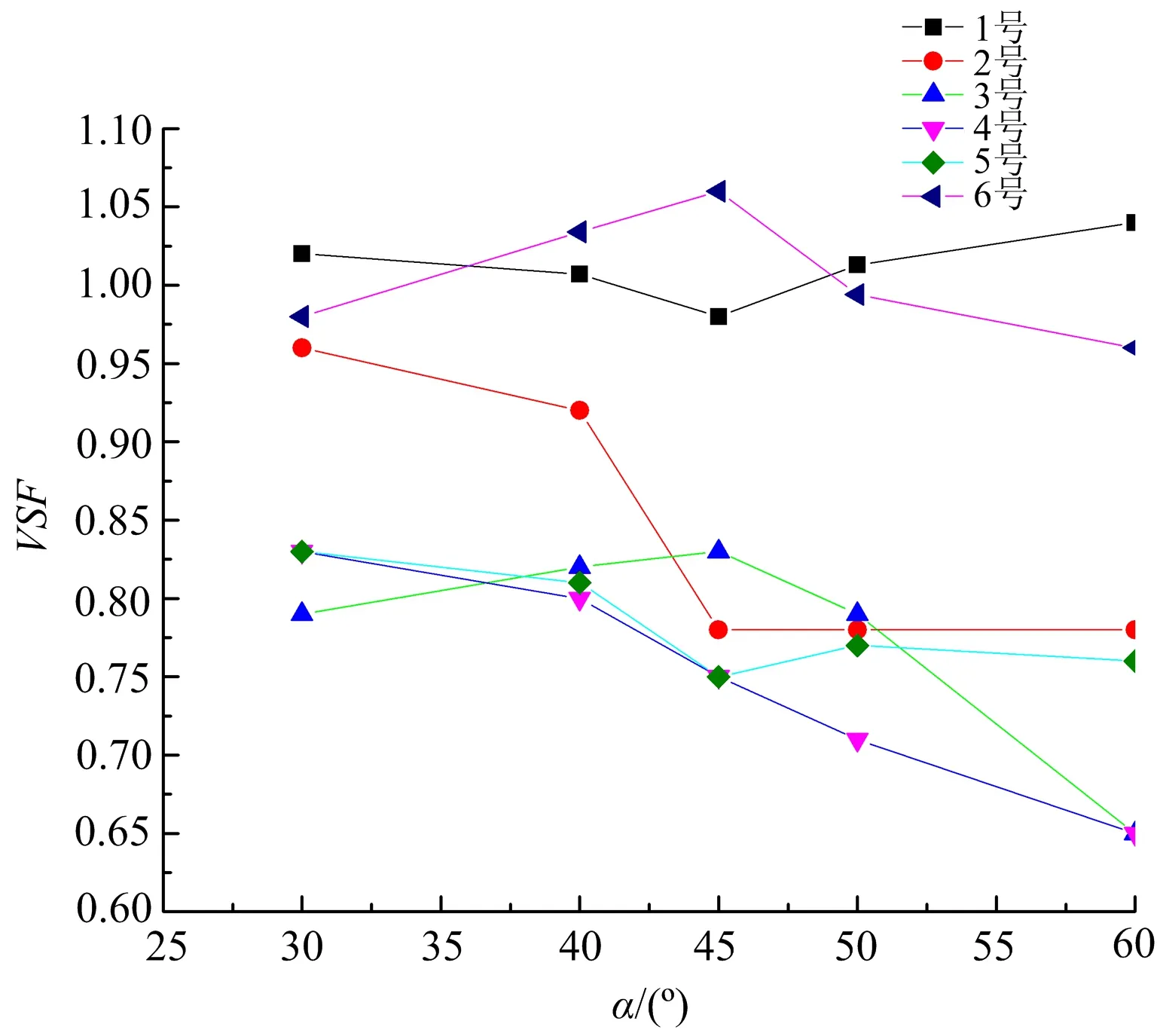
圖6 各監測點VSF隨節理傾角變化關系(K=0.5)Fig.6 The relationship between the VSF of each monitring point and the joint inclination(K=0.5)

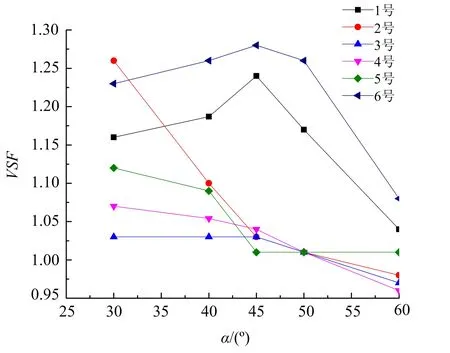
圖7 各監測點VSF隨節理傾角變化關系(K=3.0)Fig.7 The relationship between the VSF of each monitring point and the joint inclination(K=3.0)

在圖6中可以看出，當K=0.5時，1、2、5號監測點的VSF隨α增大的變化趨勢為先減小再增大，45°時為拐點。3、6號監測點的VSF隨α增大的變化趨勢為先增大再減小，45°時為拐點。4號監測點的VSF則一直減小。

在圖7中，可以看出當K=3.0時，1、3、6號VSF隨α增大的變化趨勢為先增大再減小，45°時為拐點。2、4號監測點一直減小。5號監測點的VSF隨α增大的變化趨勢為先減小再增大，45°時為拐點。

由以上分析可知，在相同等效節理剛度K下，節理傾角α對各個監測點的影響不同，對于不同等效節理剛度下，隨著α的改變，各監測點的VSF變化也不同。

3.3 節理間距對SV傳播的影響

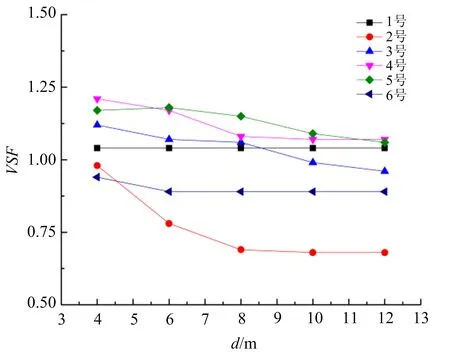
圖8 各監測點VSF隨節理間距變化關系(K=1.0)Fig.8 The relationship between the VSF of each monitoring point and the joint spacing (K=1.0)

由圖8可知，隨著節理間距d的增大，1號監測點的VSF保持不變，為一條水平直線，2～6號監測點隨著d的增加，VSF隨之減小。2號、6號監測點的VSF分別在d=6 m與d=8 m后趨于水平，其他3個監測點的VSF呈下降趨勢。觀察可以發現，d≥6 m時，在d值相同的條件下，在節理間的監測點越靠近節理1，則其VSF越小。

由此可知，1號監測點在兩條節理之前，由于不同的節理間距是由節理2控制的，而節理1是不移動的，所以在節理1位置不變時，監測點與最近的節理距離保持不變的情況下，監測點處的VSF是始終保持不變的。分析圖8中2～6號監測點折線可以發現VSF隨著節理間距d的增大都有所下降，但其減小速度越來越平緩，這說明節理間距對SV波的傳播有一定的影響，但當d大于某一值時，節理間距對SV波傳播的影響會越來越小。

4 結論

1)在節理1前監測點的VSF隨著等效節理剛度K的增大而逐漸減小。在節理間、節理2后的監測點的VSF隨著K的增大而增大。

2)隨著節理傾角的改變，不同位置的VSF表現出較為復雜的變化特性，但均在45°處出現拐點。

3)隨著節理間距d的增大，VSF在一定范圍內減小，大于這一范圍時VSF趨于穩定。