依形求義，以形表像，形義互補 數形結合在二次函數教學中的實踐探究

黃鈞軍

摘 要：二次函數是初中數學的重要內容，也是中考的一個必考的考點。二次函數對學生的思維和能力要求比較高，它可以和很多知識點綜合在一起，既可以橫向聯系，也可以縱向聯系。解決二次函數最重要的思想就是數形結合。運用數形結合可以把復雜的二次函數問題簡單化，直觀化。用數據來分析函數的圖像性質，用圖像來分析函數所表達的含義。通過數與形的相互轉化，相互表達，加深學生對二次函數知識的理解和掌握，培養學生運用數形結合的數學思想和意識。

關鍵詞：二次函數;數形結合

學生學習二次函數的內容是九年級第一學期，在學習二次函數之前，學生在八年級學習了一次函數和反比例函數，對于函數的概念有了一定的了解，一次函數是刻畫勻速變化的模型，反比例函數是刻畫定積變化的模型，而二次函數是刻畫勻變速變化的模型。學生在學習二次函數的知識過程中，對于二次函數的圖像特征把握不清晰，對二次函數的性質掌握不深刻，導致在解決二次函數的問題的時候找不到方法，或者適得其反，在二次函數的問題上花費大量時間而沒有結果，對函數的學習也失去了信心，也降低了學習數學的興趣。本文從二次函數的數和形兩方面進行教學實踐探究，通過探究二次函數的形狀來分析二次函數的性質;通過探究二次函數的數據來分析二次函數的形狀，依形求義，以形表像，形義互補，從而讓學生更好的掌握二次函數的知識。

一、以形論數，挖掘隱含條件

二次函數最重要的性質就是對稱性，單調性和最值。在學習二次函數的圖像的時候，我們從最簡單的二次函數y=ax2開始探究，然后通過平移推廣到一般的二次函數。二次函數的形狀體現了二次函數的開口方向，對稱軸的范圍，與坐標軸的交點，單調區間，最值的范圍等。在觀察二次函數的圖像的過程中，我們要深刻理解圖形所表達出來的意義，同時，挖掘圖形所隱含的條件。

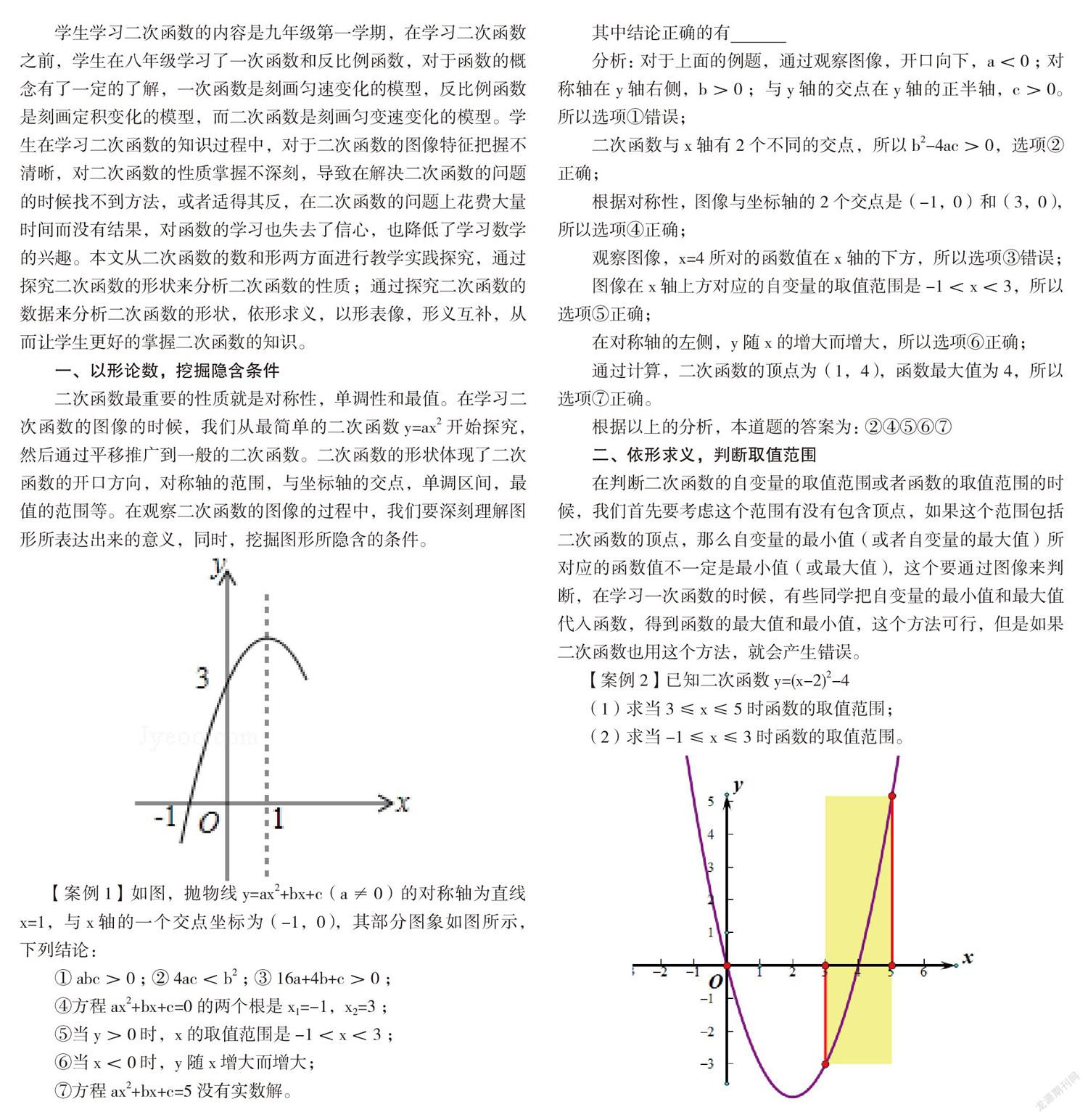
【案例1】如圖，拋物線y=ax2+bx+c（a≠0）的對稱軸為直線x=1，與x軸的一個交點坐標為（-1，0），其部分圖象如圖所示，下列結論：

①abc>0; ②4ac0;

④方程ax2+bx+c=0的兩個根是x1=-1，x2=3;

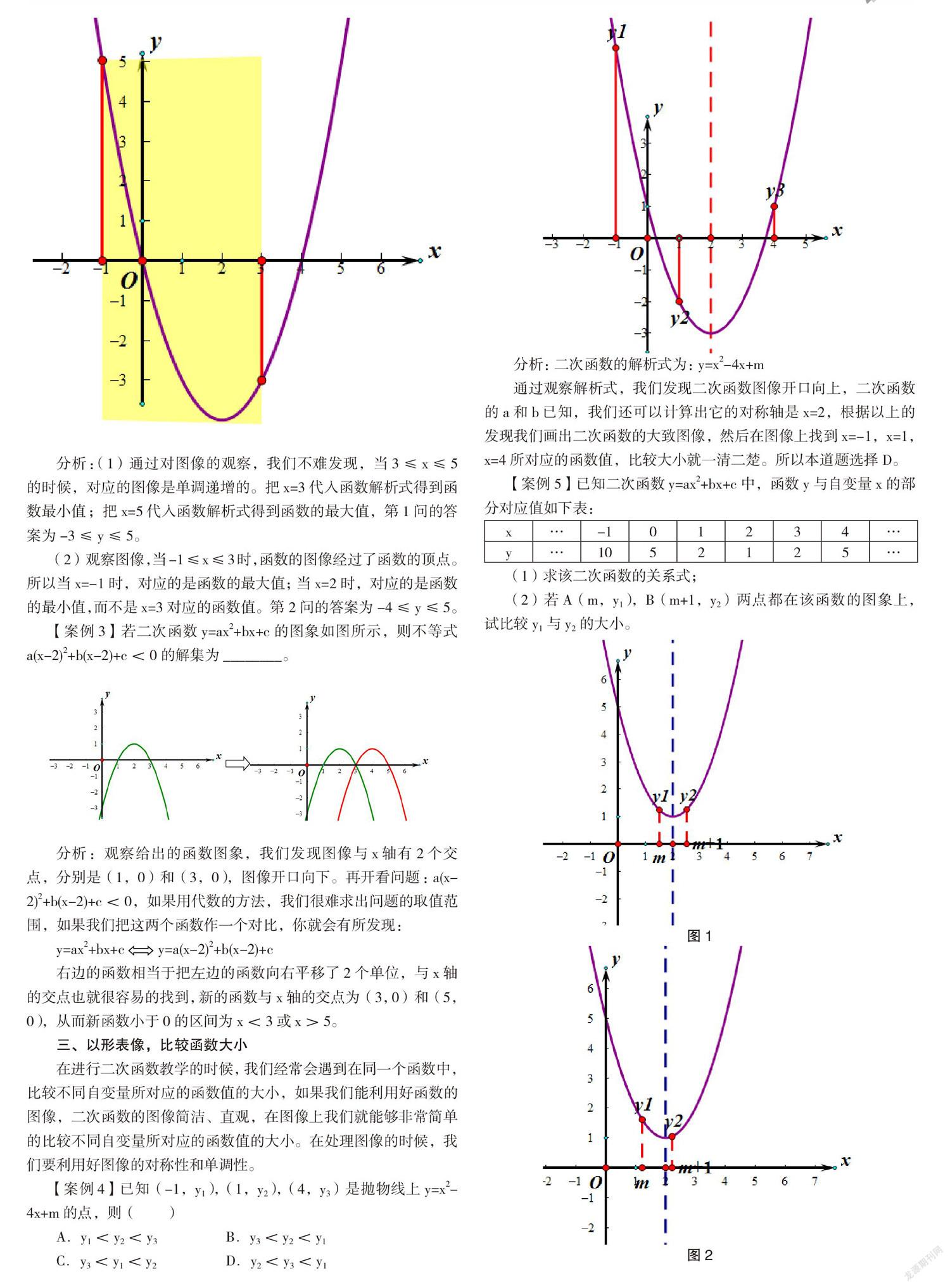
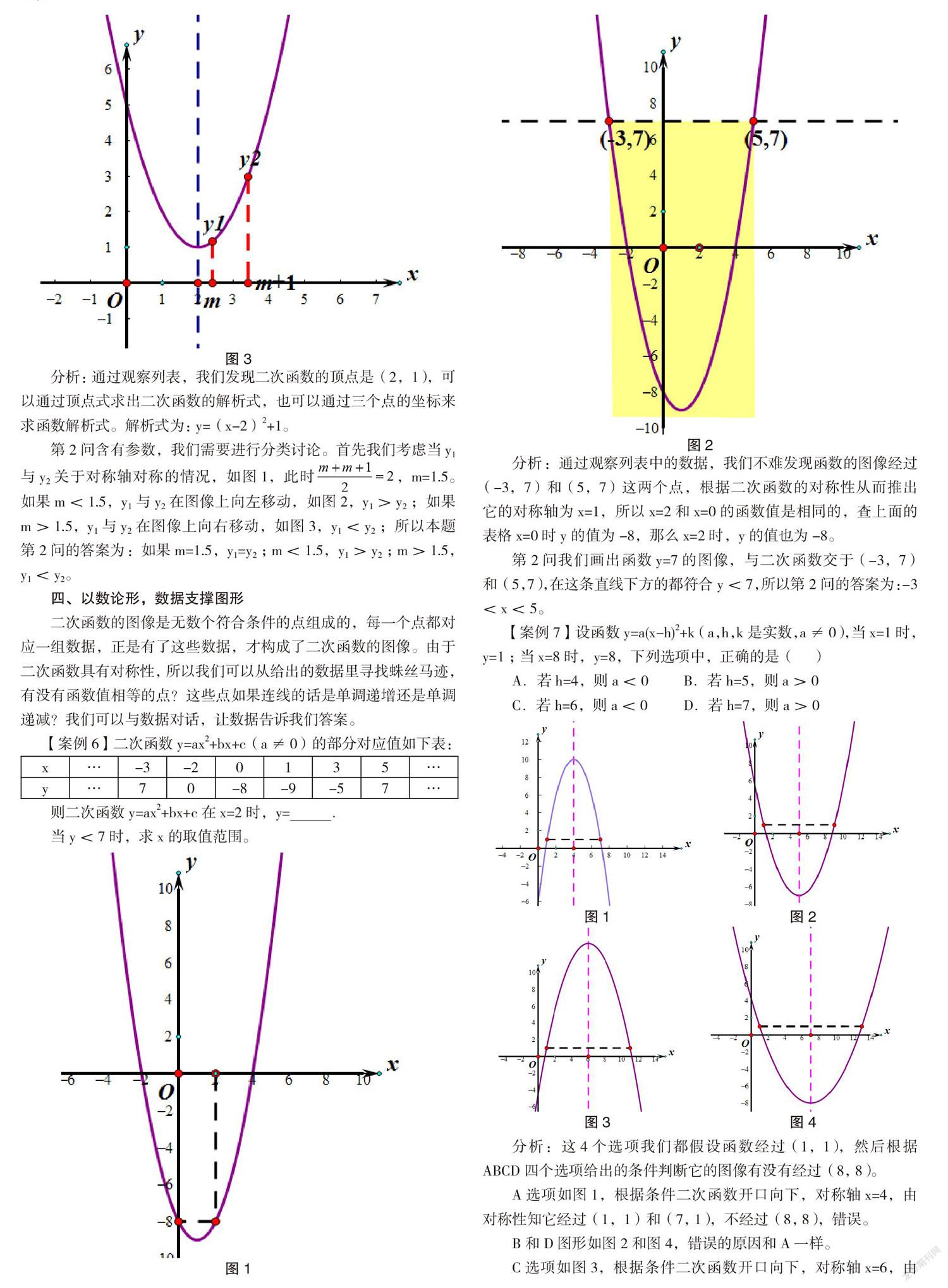
⑤當y>0時，x的取值范圍是-1

⑥當x<0時，y隨x增大而增大;

⑦方程ax2+bx+c=5沒有實數解。

其中結論正確的有

分析：對于上面的例題，通過觀察圖像，開口向下，a<0;對稱軸在y軸右側，b>0;與y軸的交點在y軸的正半軸，c>0。所以選項①錯誤;

二次函數與x軸有2個不同的交點，所以b2-4ac>0，選項②正確;

根據對稱性，圖像與坐標軸的2個交點是（-1，0）和（3，0），所以選項④正確;

觀察圖像，x=4所對的函數值在x軸的下方，所以選項③錯誤;

圖像在x軸上方對應的自變量的取值范圍是-1

在對稱軸的左側，y隨x的增大而增大，所以選項⑥正確;

通過計算，二次函數的頂點為（1，4），函數最大值為4，所以選項⑦正確。

根據以上的分析，本道題的答案為：②④⑤⑥⑦

二、依形求義，判斷取值范圍

在判斷二次函數的自變量的取值范圍或者函數的取值范圍的時候，我們首先要考慮這個范圍有沒有包含頂點，如果這個范圍包括二次函數的頂點，那么自變量的最小值（或者自變量的最大值）所對應的函數值不一定是最小值（或最大值），這個要通過圖像來判斷，在學習一次函數的時候，有些同學把自變量的最小值和最大值代入函數，得到函數的最大值和最小值，這個方法可行，但是如果二次函數也用這個方法，就會產生錯誤。

【案例2】已知二次函數y=（x-2）2-4

（1）求當3≤x≤5時函數的取值范圍;

（2）求當-1≤x≤3時函數的取值范圍。

分析：（1）通過對圖像的觀察，我們不難發現，當3≤x≤5的時候，對應的圖像是單調遞增的。把x=3代入函數解析式得到函數最小值;把x=5代入函數解析式得到函數的最大值，第1問的答案為-3≤y≤5。

（2）觀察圖像，當-1≤x≤3時，函數的圖像經過了函數的頂點。所以當x=-1時，對應的是函數的最大值;當x=2時，對應的是函數的最小值，而不是x=3對應的函數值。第2問的答案為-4≤y≤5。

【案例3】若二次函數y=ax2+bx+c的圖象如圖所示，則不等式a（x-2）2+b（x-2）+c<0的解集為________。

分析：觀察給出的函數圖象，我們發現圖像與x軸有2個交點，分別是（1，0）和（3，0），圖像開口向下。再開看問題：a（x-2）2+b（x-2）+c<0，如果用代數的方法，我們很難求出問題的取值范圍，如果我們把這兩個函數作一個對比，你就會有所發現：

y=ax2+bx+cy=a（x-2）2+b（x-2）+c

右邊的函數相當于把左邊的函數向右平移了2個單位，與x軸的交點也就很容易的找到，新的函數與x軸的交點為（3，0）和（5，0），從而新函數小于0的區間為x<3或x>5。

三、以形表像，比較函數大小

在進行二次函數教學的時候，我們經常會遇到在同一個函數中，比較不同自變量所對應的函數值的大小，如果我們能利用好函數的圖像，二次函數的圖像簡潔、直觀，在圖像上我們就能夠非常簡單的比較不同自變量所對應的函數值的大小。在處理圖像的時候，我們要利用好圖像的對稱性和單調性。

【案例4】已知（-1，y1），（1，y2），（4，y3）是拋物線上y=x2-4x+m的點，則（ ）

A.y1

C.y3

分析：二次函數的解析式為：y=x2-4x+m

通過觀察解析式，我們發現二次函數圖像開口向上，二次函數的a和b已知，我們還可以計算出它的對稱軸是x=2，根據以上的發現我們畫出二次函數的大致圖像，然后在圖像上找到x=-1，x=1，x=4所對應的函數值，比較大小就一清二楚。所以本道題選擇D。

【案例5】已知二次函數y=ax2+bx+c中，函數y與自變量x的部分對應值如下表：

x … -1 0 1 2 3 4 …

y … 10 5 2 1 2 5 …

（1）求該二次函數的關系式;

（2）若A（m，y1），B（m+1，y2）兩點都在該函數的圖象上，試比較y1與y2的大小。

圖1

圖2

圖3

分析：通過觀察列表，我們發現二次函數的頂點是（2，1），可以通過頂點式求出二次函數的解析式，也可以通過三個點的坐標來求函數解析式。解析式為：y=（x-2）2+1。

第2問含有參數，我們需要進行分類討論。首先我們考慮當y1與y2關于對稱軸對稱的情況，如圖1，此時，m=1.5。如果m<1.5，y1與y2在圖像上向左移動，如圖2，y1>y2;如果m>1.5，y1與y2在圖像上向右移動，如圖3，y1y2;m>1.5，y1

四、以數論形，數據支撐圖形

二次函數的圖像是無數個符合條件的點組成的，每一個點都對應一組數據，正是有了這些數據，才構成了二次函數的圖像。由于二次函數具有對稱性，所以我們可以從給出的數據里尋找蛛絲馬跡，有沒有函數值相等的點？這些點如果連線的話是單調遞增還是單調遞減？我們可以與數據對話，讓數據告訴我們答案。

【案例6】二次函數y=ax2+bx+c（a≠0）的部分對應值如下表：

x … -3 -2 0 1 3 5 …

y … 7 0 -8 -9 -5 7 …

則二次函數y=ax2+bx+c在x=2時，y= ? .

當y<7時，求x的取值范圍。

圖1

圖2

分析：通過觀察列表中的數據，我們不難發現函數的圖像經過（-3，7）和（5，7）這兩個點，根據二次函數的對稱性從而推出它的對稱軸為x=1，所以x=2和x=0的函數值是相同的，查上面的表格x=0時y的值為-8，那么x=2時，y的值也為-8。

第2問我們畫出函數y=7的圖像，與二次函數交于（-3，7）和（5，7），在這條直線下方的都符合y<7，所以第2問的答案為：-3

【案例7】設函數y=a（x-h）2+k（a，h，k是實數，a≠0），當x=1時，y=1;當x=8時，y=8，下列選項中，正確的是（ ? ? ）

A.若h=4，則a<0 B.若h=5，則a>0

C.若h=6，則a<0 D.若h=7，則a>0

圖1 圖2

圖3 圖4

分析：這4個選項我們都假設函數經過（1，1），然后根據ABCD四個選項給出的條件判斷它的圖像有沒有經過（8， 8）。

A選項如圖1，根據條件二次函數開口向下，對稱軸x=4，由對稱性知它經過（1，1）和（7， 1），不經過（8， 8），錯誤。

B和D圖形如圖2和圖4，錯誤的原因和A一樣。

C選項如圖3，根據條件二次函數開口向下，對稱軸x=6，由對稱性知它經過（1，1）和（11， 1），有可能經過（8， 8），所以選項C正確。

五、形義互補，回歸問題本源

二次函數命題的形式比較多，命題者想盡千方百計來考查學生對知識的掌握。面對一些新題型，很多同學感到力不從心。但是如果我們抓住了問題的核心，處理起來就能夠得心應手。面對二次函數問題，我們首先分析問題的條件，有些問題是二次函數與其它函數的關系，有些問題是二次函數的對稱性問題，有些問題是二次函數的單調性，有些問題是比較二次函數值的大小，知道了解決的問題方向，我們就能夠順著這個方向抽繭剝絲，解決問題。

【案例8】已知a是方程的實數根，則直線y=ax+2-c的圖像大致是（ ? ?）

A B

C D

分析：判斷直線y=ax+2-a所經過的象限，我們必須知道a的范圍。a是方程的實數根，這個根的范圍我們如何確定呢？我們可以通過畫圖像來解決。

假設y1=x2-4x，，在同一個直角坐標系中畫出上面2個函數的圖像，我們發現它們在第一象限有交點，并且交點的橫坐標大于2，所以我們可以判斷a>2，那么所求直線y=ax+2-a經過一三四象限，正確答案為A。

【案例9】已知函數y1=x2-（m+2）x+2m+3，y2=nx+k-2n（m，n，k為常數且n≠0）.若函數y1，y2的圖象始終經過同一定點M。

（1）求點M的坐標和k的值。

（2）若m≤2，當-1≤x≤2時，總有y1≤y2，求m+n的取值范圍。

分析：y1=x2-mx-2x+2m+3，解析式里含有參數m，過定點說明與m無關，解析式可以化為：

（2-x）m+x2-2x+3-y1=0，所以x=2，y1=3，定點是（2， 3）。定點坐標代入一次函數解析式得k=3。

第2問我們利用好圖像。二次函數和一次函數都經過了定點（2， 3），二次函數開口向上，由于m≤2，所以對稱軸≤2，當-1≤x≤2時，總有y1≤y2，也就是說-1≤x≤2時，y2的圖像總在y1的上方，當x=-1時，-1所對的一次函數值大于或等于-1所對的二次函數值即可。根據以上分析可得：

（-1）2-（m+2）（-1）+2m+3≤-n+3-2n，化簡后得：m+n≤-1

在二次函數的解答過程中，我們要仔細分析好題目的條件，深刻理解二次函數的數和形的關系，利用好它們的關系，我們可以把復雜問題簡單化，綜合的問題直觀化。在分析二次函數的數與形的時候，我們要把握好關鍵數據和圖像特征，按照以下流程來分析：

綜上所述，數形結合是解決二次函數的橋梁，數形結合揭示了二次函數題目知識點之間的內在聯系，既分析了代數的意義，又顯示了幾何直觀，使數量的刻畫和圖形的直觀充分融合，教師在實際教學過程中，要培養學生這種思想方法，不僅可以幫助學生更好的理解和掌握知識，還能夠發展學生的抽象思維能力，培養學生直觀想象能力，從而達到提高學生核心素養的要求。