適應性FCM聚類分析對導軌溫度特征的改進研究

李志偉

（四川建筑職業技術學院，四川 德陽618000）

關鍵字：適應性FCM聚類算法；導軌；溫度測點；改進研究

0 引 言

機床導軌熱特性研究的關鍵是其溫度測點改進設計，通常在進行導軌熱變形補償分析前，要對其進行環境溫度與變形檢驗，并以此為依據建立相應的熱變形誤差模型[1-2]。由于導軌工作時易受到外部環境及參數變化的影響，其溫度場具有時變性。為了解導軌溫升和熱變形情況，需在導軌相應位置設置溫度傳感器，但考慮成本和導軌的工況，以及相應建模時處理數據量較多等情況，同時在導軌上安裝過多溫度測點會使各測點產生干涉現象降低預測精度，所以必須先對導軌的溫度測點進行合理分組分析，以增強模型預測的準確性[3]。

采用適應性FCM聚類算法改進溫度測點時，需保證選擇關鍵參數的真實性，選取樣本分類數c及加權指數m作為關鍵參數[4-5]。在分析中要確保c的準確，以至于確定聚類數有效性，m對分析模型目標函數的斂散性及一致性有關鍵聯系。加權指數m取3具有較好的收斂性，但聚類數C在不同情況下存在一定的隨意性，為了保證分析結果的準確性，需對聚類數C的選取進行改進優化[6]。

1 適應性FCM算法分析與建模

普通的FCM聚類算法對機床溫度測點優化，一般算法中的設置分類數需人為設定，由于經驗及其他因素的影響，將導致分析結果出現較大的偏差，同時分析結果的有效性需依賴有相關工程經驗的專業人員進行判斷，耗時耗力[7]。

進行分類的目的是將數據集合進行分組，同時需保證各組間的間距要大，而每組數據個體間的間隔盡可能小。按照該方法，為保障分析結果的準確性，需對FCM聚類算法進行適應性改進，調整后的聚類數C的自適應函數為

分析得出，改進后的適應性函數L（c）的分母為組間距，分子為各組內數據點間的間距，由此得出結論：L（c）的值越大，則分類越準確，相應的分類數也越有效。由于導軌的運行參數為常規空載條件運行，其他系統保持不變，當導軌在工作狀態時，設置X向移動速度為2 mm/min，工作時間為1 h, 再梯級遞進移動的試驗方案，相應每隔300 s采集一次數據。其他條件保持不變，當加權指數m取值為3，即可保持良好的一致性。以傳統算法為理論基礎，得到聚類數C的自適應函數如下：

1）理論初始計算條件：設置迭代收斂條件ε≥0，原始分類數目c=1，當分類數c為1時,自適應值L（c）=1，相應原始分類矩陣v（0）,同時計數器b歸零。

4）用一個矩陣范數||·||比較vk和v（k+1），若｜|v（k+1）－vk||≤ε，則迭代終止，否則，設b=b+1，轉向步驟1）繼續迭代，直至滿足要求。

5）計算L（c），若自適應函數滿足L（c-1）≤L（c-2）且L（c-1）≥L（c），即自適應分類結束，否則，設c=c+1，轉向步驟1）繼續迭代，直至滿足要求。

2 適應性FCM聚類算法在導軌溫度測點改進分析實例

適應性FCM聚類算法，能自動對機床導軌溫度測點進行建模仿真并合理優化分組，且分類結果準確，在實際的應用中具有一定的前景。

為了能夠對導軌的溫度測點進行準確分析，在實際研究中將該算法應用于導軌的溫度測點優化。通過ANSYS對導軌瞬態熱變形仿真建模分析基礎上，根據研究的具體情況調整分析過程，以導軌在工況空載條件下的瞬態溫度場及熱變形狀況為研究對象，并布置若干測點以實時監測溫度，方便準確獲取監測點的溫升與熱變形狀況，測點分布位置導軌上端1、左端2、右端3、前端4、后端5，如圖1所示。

為確保試驗有效，導軌采用移動速率遞進方式進行工作，前1 h內移動速率為2 mm/min，然后在速率為2.5 mm/min 繼續工作1 h，同時每間隔300 s采集一次測點的試驗數據，當前溫度為室溫20 ℃。為了保證各測點的時效性及準確性，對各測點的狀態進行分析得到相應的時頻圖，如圖2 所示。

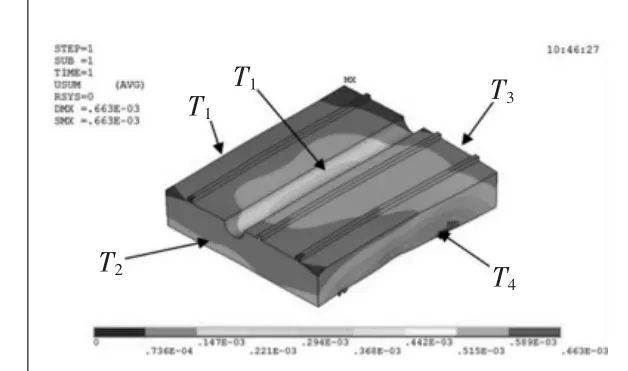
圖1 測點分布位置圖

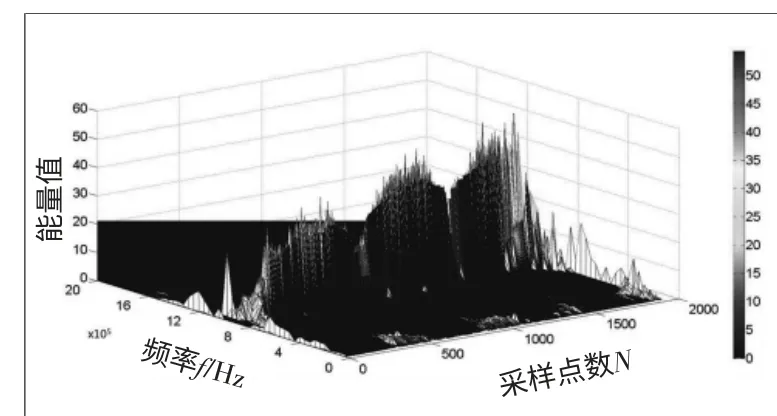
圖2 自適應函數的時頻圖

通過時頻圖分析，各測點溫度能量值響應靈敏（測點能量值單位為℃），監測的溫度準確有效，能夠反映真實加工狀態，基于適應性FCM聚類改進算法對導軌溫度測點實施分組優化，m取3，當C取3類時，試驗終止，L（c）計算值如下：L（2）=331.437，L（3）=398.385，L（4）=353.012，L（5）=326.253。L（c）的變化過程如圖3所示。滿足理論設定條件，經分析分組為3類時分析結果最佳，結果越準確。同時得到各測點的實時監測溫度，如表1所示。

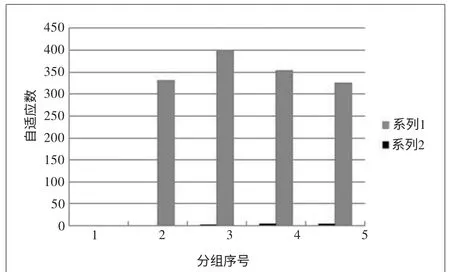
圖3 適應性分組數分布柱狀圖

為了保證導軌測點分組的準確性，需計算各測點的可靠性，通過建立測點的可靠性計算模型，設傳遞變量為對數函數，將測點溫度作為學習樣本，利用高斯函數，設k為迭代步數，當k次迭代的閾值中心為u1（k）、u2（k）、…、un（k），對應的域為φ1（k），φ2（k）、…、φn（k）。計算步驟為：

1）計算參數輸入和閾值中心的間距‖yj－Ui（k）‖。其中：i=1，2，…，n；j=1，2，…，m。

2）參數樣本yj，以最小間距法則對應分組。

3）重置新的閾值中心：

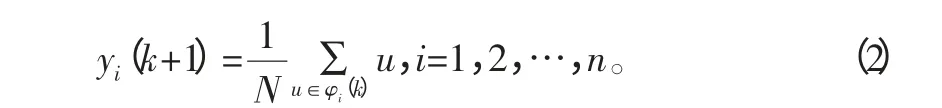
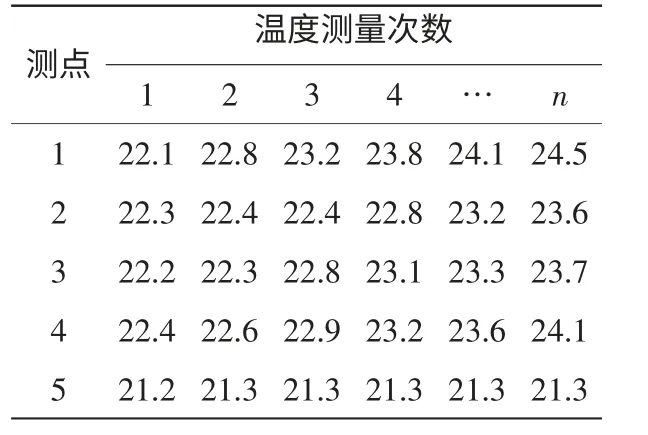
表1 測點溫度數據 ℃

其中：N為第i個閾值范圍φi（k）中含有的參數。

4）當yi（k+1）≠yi（k），重回步驟1），否則計算終止。

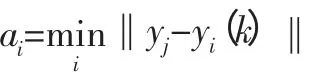
6）用Matlab語言對溫度測點進行關聯度模擬。

由上述過程，建立了導軌溫度測點的可靠性模型，通過步驟1）～6）計算得到對應測點的可靠度R（i,j）。溫度測點的可靠性模糊分組矩陣如表2所示。

根據之前的分析結果，確定將所有測點分成3組。通過對比有用測點的數據，確定選擇第3類測點的可靠性數據，并按照數據關聯度重新對各測點進行分組歸類。第一組：1#；第二組：2#、3#；第三組：4#、5#。

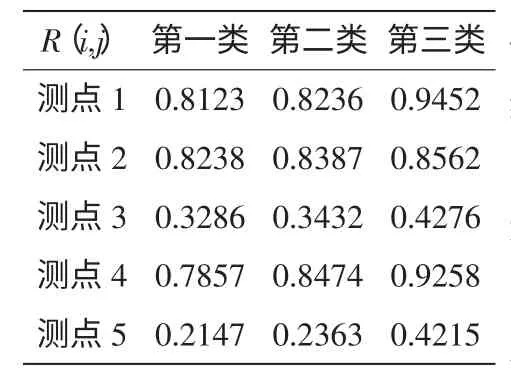
表2 溫度測點的可靠性模糊分組矩陣

同時利用相關系數法挑選每組中一個重要測溫點作為溫度測點研究，由表2按測點的可靠性系數，得到各測點間的關聯系數如表3所示，最終取1#、2#、4#測點為導軌的關鍵測點。

3 結 論

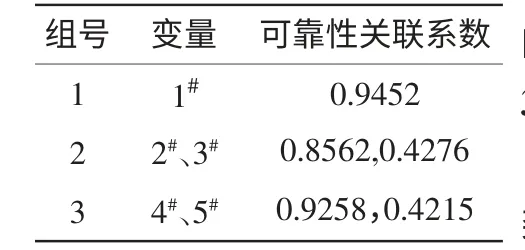
表3 導軌溫度測點的相關系數表

本文采用適應性FCM聚類分析算法對導軌測點進行改進分析，其原理為依據導軌溫度及熱變形量，增設聚類數C的適應性目標函數，建立相應的適應性FCM聚類分析算法可靠性模型，通過建模得到多元回歸關鍵測點熱誤差分析數據。為了得到準確的溫度測點，將聚類數自適應算法施加到導軌的測溫點改進上，將導軌的關鍵測點由5個減少到3個。實踐證明，該算法不僅能給出最佳聚類數，還能對測點進行分組優化，其測點分類情況與實際情況更加吻合。該方法為機床溫度測點可靠性分析研究開辟了新的途徑，具有廣闊的應用前景。