嵌入式數控系統速度前瞻規劃算法研究

游達章，余 煉，張 敏，康亞偉

(湖北工業大學 機械工程學院， 武漢 430068)

速度和加速度突變引起的沖擊對零件加工精度和表面質量有很大影響，速度突變引起的沖擊為剛性沖擊，而加速度突變引起的沖擊為柔性沖擊。在梯形加減速當中，速度突變往往來源于加工路徑方向的改變，加速度突變則主要體現在電機在加減速過程中加速度從無到有或者從有到無的過程。一方面，為了追求高效而使電機頻繁地加速，使之盡可能達到理想的最大速度；另一方面，為了減少沖擊而使電機頻繁地減速，使得電機成為了加減速的矛盾綜合體，導致電機頻繁加減速，進而影響了電機的使用壽命和加工精度。為了兼顧高效和平穩，對整個插補過程提前做好加減速規劃十分必要，減少電機加減速頻次通常作為主要手段。為此，不少學者投入了很大精力研究。

王濤等[1]設計了一種利用圓弧轉接的軌跡規劃算法為減少因加工路徑方向改變引起的剛性沖擊提供了很好的解決思路。陳良驥等[2]根據相鄰路徑的轉角建立了可直接進行段間轉接的條件以及條件不成立的修正方法，此外還給出了段內加減速的處理方法，使加工效率得以較大提高，尤其適用于程序量較大的情形，但并沒有充分論述段內加減速和段間轉接的直接聯系。王耀庭等[3]分析了高速加工微小線段銜接速度計算的約束條件，提出了一種加工軌跡速度前瞻段數自適應控制算法，有效簡化了連接點銜接速度的計算方法，減少了啟停次數，但是效率仍然有提升的空間。葉偉等[4]以離散的方法建立了一種全新的插補算法使得加減速控制連續平滑，小線段加工過程具有較高的運行速度，但是基于S型加減速的，實際應用起來比較復雜，并不適用于一般的嵌入式數控系統。董靖川等[5]提出的通用型前瞻速度規劃算法進一步節約了加工時間并提高了加工質量，黃昕等[6]提出的基于雙向掃描算法實現了連續小段路徑之間的高速銜接，但以上二者算法本質還是連續多段前瞻算法，都并未充分論證規劃元大小(即一次連續規劃段數)對加工效率和平穩性的影響，具有一定的局限性。張立先等[7]提出的前瞻處理與動態修調方法有效地提高了整體加工速度，所謂的動態修調方法即滿足反向速度可達性條件，即第i段末速度要小于初速度的情形，但初衷并不是保證最后一個直線段的出口速度為0，仍未主動避免最后一個直線段出口速度突變為0引起的剛性沖擊。

為了進一步兼顧高效平穩，首先分析了連續多段前瞻算法存在的局限性；其次在連續多段前瞻算法的基礎之上做了改進，提出了單段前瞻后顧算法；最后通過仿真實驗，對比分析了3種不同速度規劃算法的效率和平穩性。結果表明，單段前瞻后顧算法能有效避免單次連續規劃段數對效率和平穩性的影響，且能夠有效減少電機加減數次數，執行效率也得到了小幅提升，與前人相比有不同程度提高。此外，算法能夠在嵌入式數控系統平臺(STM32F407)上實現，測量結果與仿真吻合。

1 初步規劃

為了使規劃算法更具一般性，通常在規劃軌跡的運動參數之前，將圓弧打斷為連續微小直線段，李彥奎等[8]已經提出了比較成熟的打斷算法，此處不再贅述。打斷之后軌跡平滑度下降勢必導致加工路徑方向的改變，從而引發速度方向突變進而產生剛性沖擊。為了減少沖擊，需要在到達拐點之前按照某種方法將速度降至合適的范圍內以實現平穩過度，以上計算拐角速度過程稱之為初步規劃。

如圖1所示，已知第i段與第i-1段線段夾角θ。視兩段直線拐角Pi處為半徑很小的圓周運動，由幾何關系知

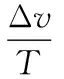
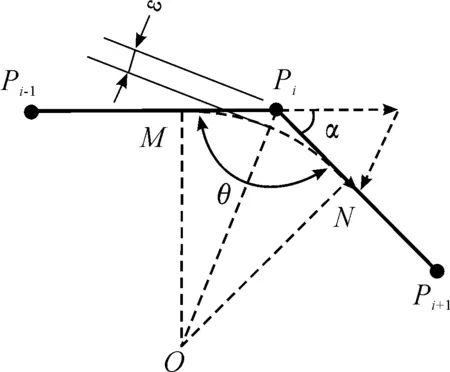
圖1 圓周運動模型示意圖

2 連續多段前瞻規劃算法

2.1 連續多段前瞻規劃算法原理

假設一段連續加工軌跡有n段直線，每次連續規劃段數為N，那么至少需要n/N或n/N+1次才能完成整段加工軌跡的規劃。視起點到終點為一個連續的加速過程，從終點到起點為一個連續的反向加速過程。連續多段前瞻規劃算法原理如圖2所示。

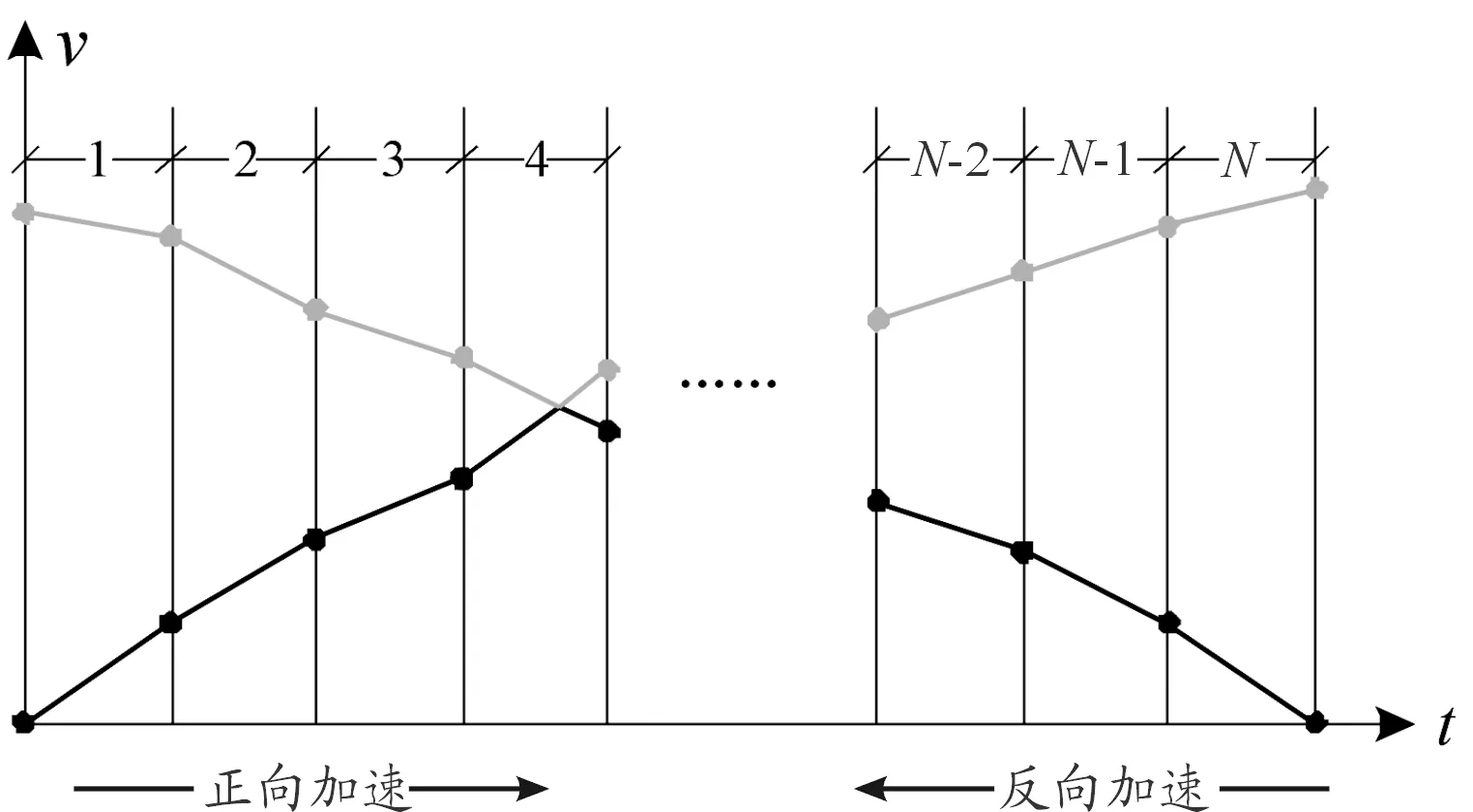
圖2 連續多段前瞻規劃算法原理示意圖

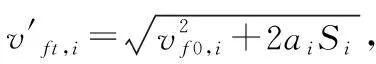
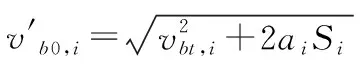
將以上兩個過程疊加，取v0,i=min{vf0,i,vb0,i}，vt,i=min{vft,i,vbt,i}，分別作為第i段直線的入口速度和出口速度。

2.2 不同規劃段數對連續多段前瞻算法的影響

為了研究單次連續前瞻規劃段數對效率和平穩性的影響，用連續多段前瞻算法驗證以下一段G代碼，對應軌跡如圖3所示。得到效率和平穩性隨規劃段數的變化關系，如表1所示。

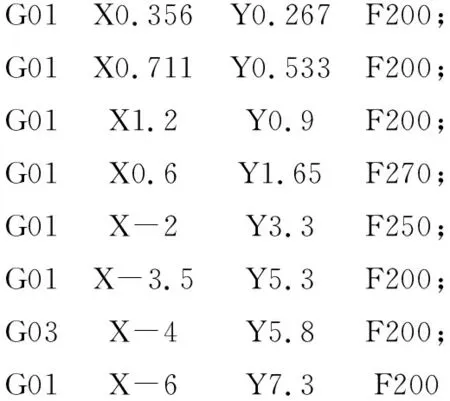
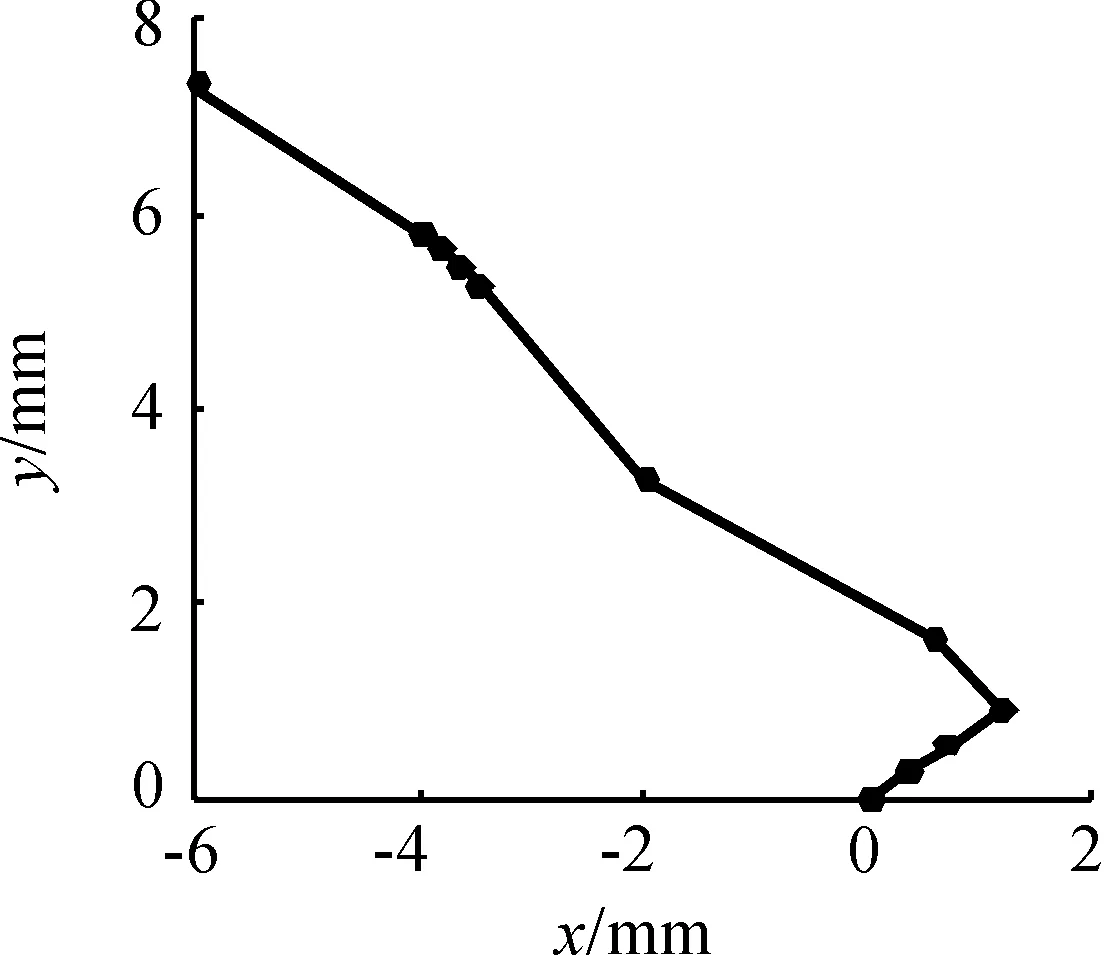
圖3 插補軌跡

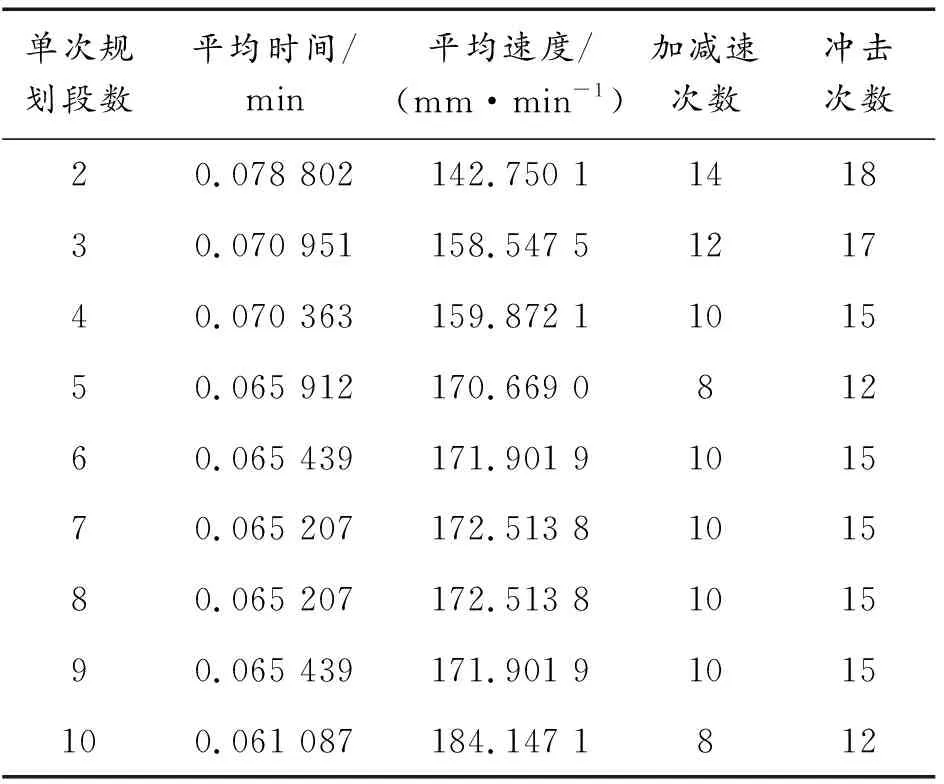
表1 規劃段數對連續多段直線前瞻算法的影響

表1中多出的3段來自被打斷的圓弧。由表可知，規劃段數與平均速度相關性顯著(R=0.895 5，P=0.001 1)，但與加減速次數和沖擊次數相關性均不顯著(R=-0.688 6，P=0.040 2；R=-0.620 5，P=0.074 6)。換而言之，對于連續多段前瞻算法而言，增加單次規劃段數雖然能夠提高效率，但是并不確定能減少沖擊，因而設計人員在選擇規劃段數的過程中可能會出現一定的盲目性。此外，過分追求的規劃段數會可能額外增加算法時間復雜度和空間復雜度，對系統實時性可能有潛在影響，存在一定局限性。

3 前瞻后顧規劃算法

在本文第1節中完成了初步規劃，得到第i段直線與第i+1段直線之間的拐角速度vmj,i；在本文第2節中分析了連續多段前瞻算法的局限性。為了避免單次連續規劃段數對平穩性和效率的影響，以及保證整個插補過程的最后一段直線出口速度為0和無沖擊地完成每段插補距離S，提出了一種前瞻后顧算法來同時滿足以上需求。

3.1 前瞻原則

假設當前第i段直線為所有插補過程中的最后一段，為了保證當前第i段的出口速度vt,i為0，以消除末速度突變引起的剛性沖擊，在加速度(視為反向加速過程)ai與加速距離Si已知的條件下，那么第i段的入口速度(即前瞻速度vf,i)需滿足如下條件：

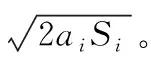
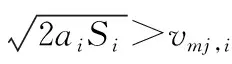
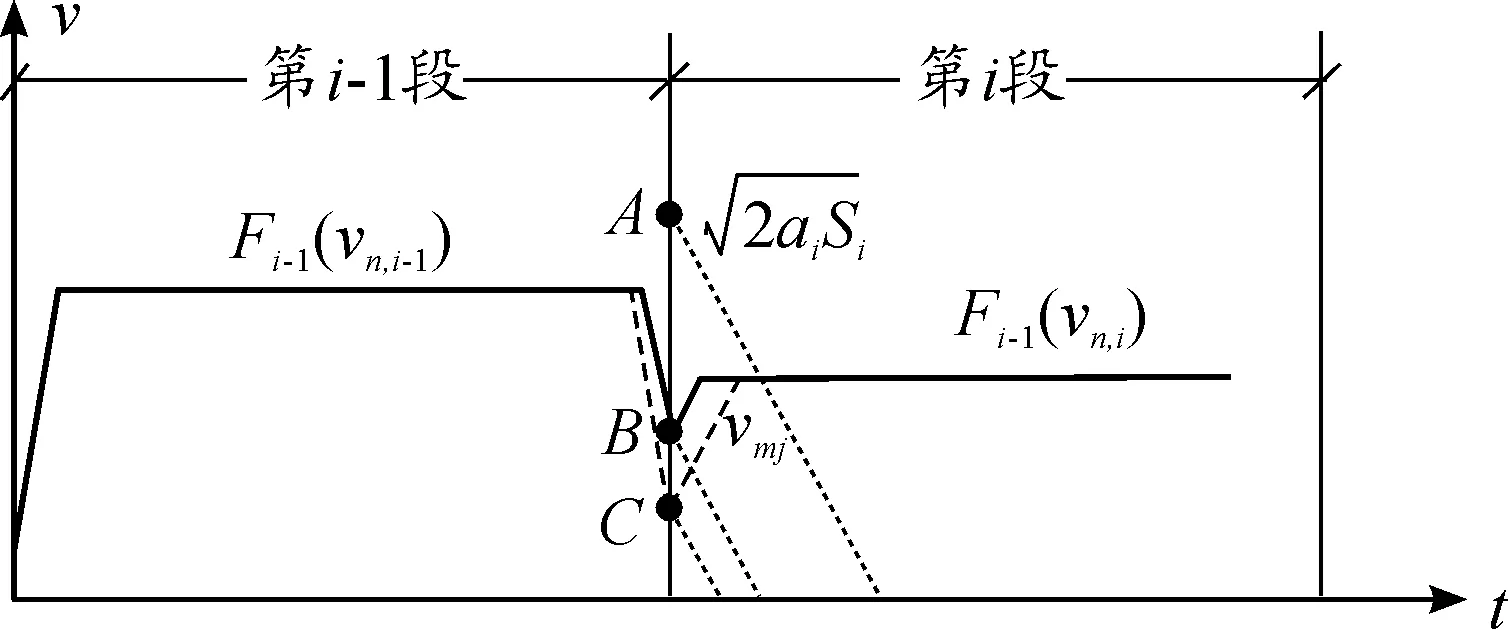
圖4 前瞻原則示意圖

3.2 后顧原則

由于第i-1段直線的入口速度已經被規劃好且為v0,i-1，且加速度(視為正向加速過程)ai-1與加速距離Si-1已知，為了消除出口速度突變產生的剛性沖擊，那么第i-1段的出口速度(即后顧速度vb,i)滿足以下條件：

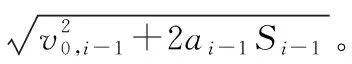
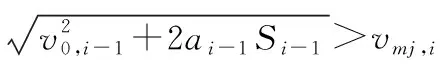
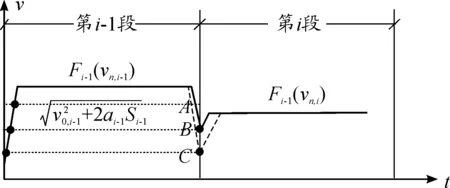
圖5 后顧原則示意圖

3.3 前瞻后顧原則算法應用

為了同時兼顧最大拐角速度vmj,i，第i段前瞻速度vf,i以及第i段后顧速度vb,i，得到第i段的最終入口速度(也即第i-1段的出口速度)并規定第1段的入口速度v0,1=0，按照前瞻后顧原則，可規劃得到所有線段之間最終的銜接速度。動態規劃過程如圖6所示。

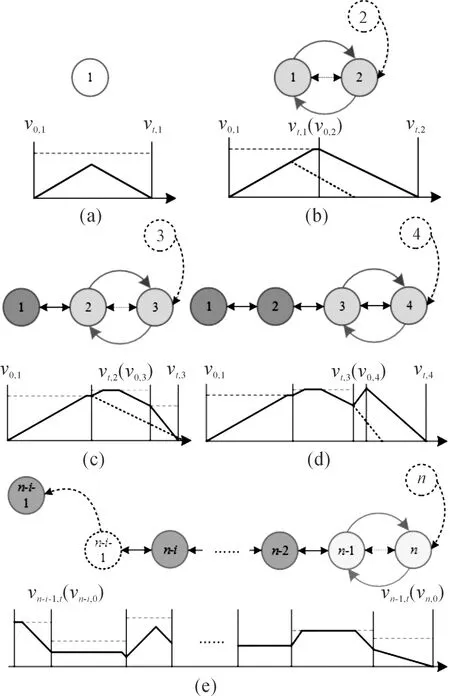
圖6 動態規劃過程示意圖

只有一條直線段時，入口速度和出口速度均為0，如圖6(a)所示。若有新的直線需要規劃，則根據新的直線與上一條直線的夾角計算拐角速度，根據前瞻后顧原則計算前瞻速度和后顧速度，取三者最小值作為新加入直線的入口速度，根據前瞻原則，新加入直線的出口速度為0，如圖6(b)所示。而后繼續判斷是否有新的直線加入規劃過程，若有，則重復上述過程。當直線總段數n過大時，會占用很大內存，為了減少內存開銷，可以將以上規劃過程放入隊列中。

以上規劃過程流程如圖7所示。

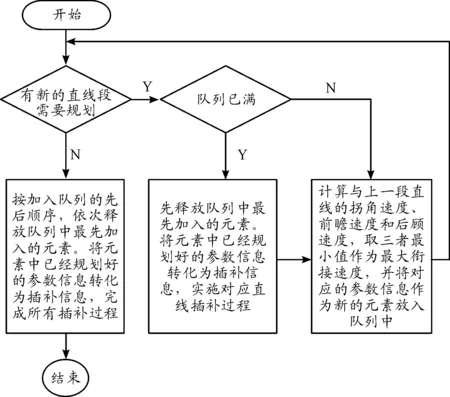
圖7 動態規劃流程框圖

4 算法驗證

4.1 前瞻后顧規劃算法實例驗證

為進一步驗證結果，用以上算法運行2.2節中G代碼，得到規劃過程如圖8所示。

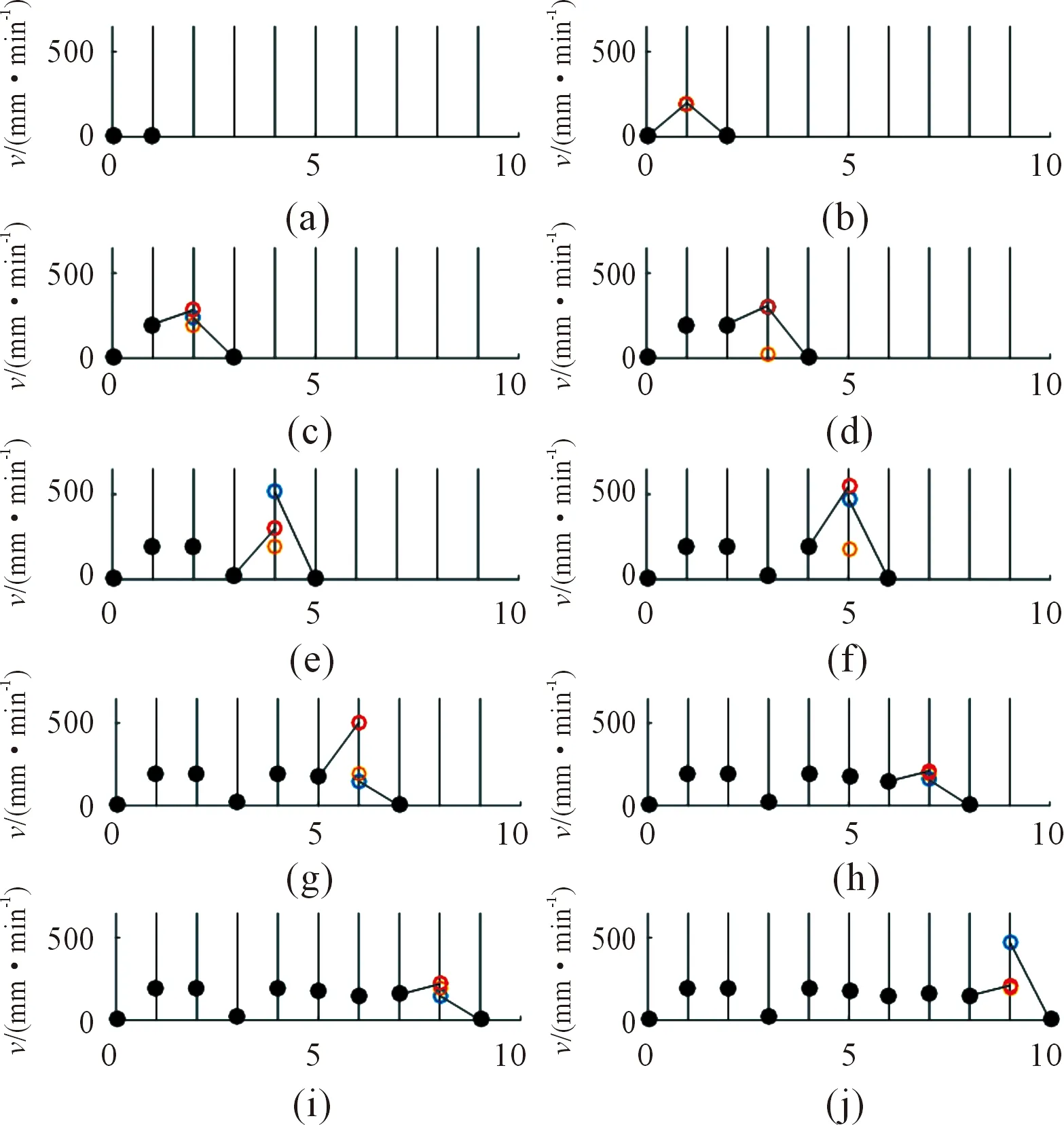
圖8 前瞻后顧規劃過程

以圖8(e)為例，第4段直線與第5段直線銜接處從上到下依次為前瞻速度、后顧速度和拐角速度，取三者之中較小者并規定為第5段最終的入口速度，如圖8(f)所示。而后再次讀入一段新的直線參數信息，繼續規劃第5段與第6段之間的拐角速度、前瞻速度和后顧速度，再次取較小者規劃第6段的入口速度……以此類推，其中第一段默認入口速度為0。從圖8中可以看出，在未知G代碼段數的情況下，也能嚴格保證最后一段的出口速度降為0，以消除速度突變產生的剛性沖擊。

4.2 不同規劃算法實例驗證

仍然以2.2節中G代碼為例，分別使用不含前瞻算法、含前瞻后顧算法以及連續多段前瞻算法執行，得到速度-時間關系如圖9所示，能直觀地看到含前瞻后顧算法比他兩種方法的效率都高；與不含前瞻算法相比，能顯著減少加減速頻次。

以STM32F407作為嵌入式數控系統平臺為例，通過瞬時速度和相鄰兩次插補時間的關系，計算得到定時計數周期。使用串口打印出定時計數周期來計算實時插補速度，得到速度-時間關系曲線，如圖10所示，從而驗證了單段直線前瞻后顧算法的可實現性，與仿真結果相吻合。

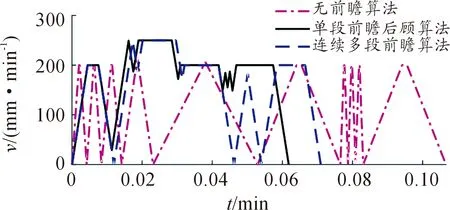
圖9 3種不同算法仿真結果

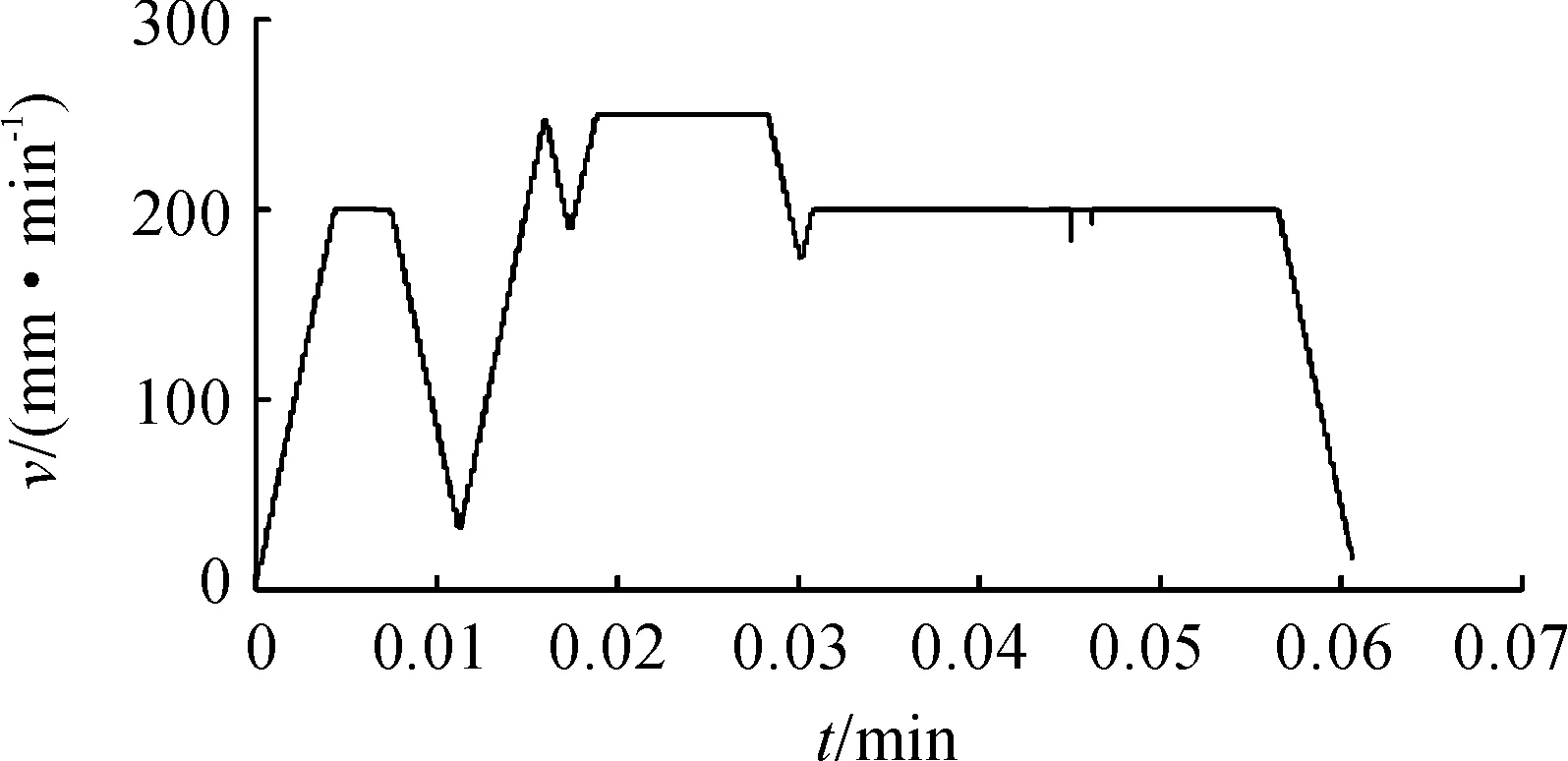
圖10 前瞻后顧規劃算法在嵌入式數控系統平臺上實現時得到的速度-時間關系曲線

5 結果評價分析

從表2來看，仍然以2.2節中的G代碼為例。連續多段前瞻算法以每次規劃2段為例，單段直線前瞻后顧算法從效率和平穩性來看表現更好，其中效率比無前瞻算法提高了72.56%，比連續多段前瞻算法提升了27.48%；其中加減數次數比無前瞻算法減少了30%，與連續多段前瞻算法相等；柔性沖擊次數比無前瞻算法減少了34.49%，比連續多段前瞻算法多了1次。

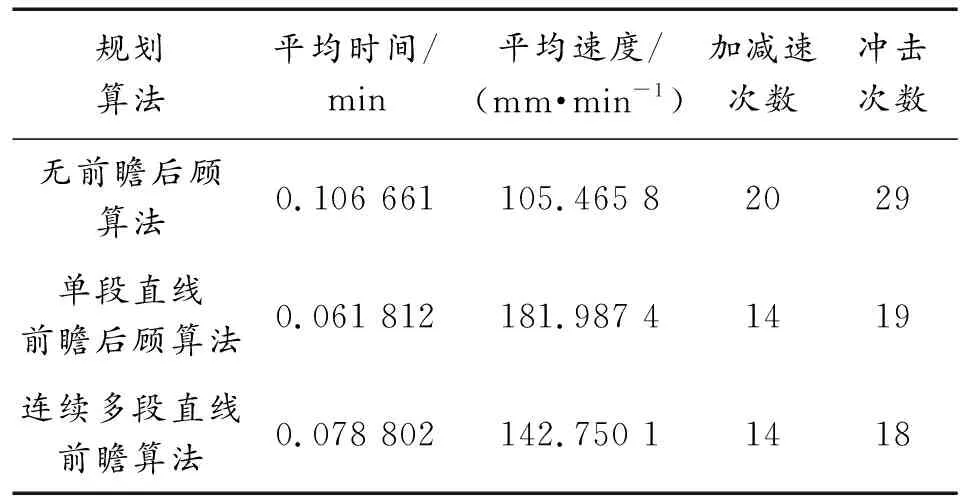
表2 3種不同算法計算結果

從表3來看，通過使用含前瞻后顧規劃算法來執行文獻[2-3]中給出的G代碼，仿真結果顯示，效率比文獻[2]略微提高了14.7%，比文獻[3]高出了64.87%。文獻中加減速次數和沖擊次數未給出，不具備對比條件。

表3 相關文獻計算結果

綜上所述，在嵌入式數控系統應用當中，前瞻后顧算法在效率和平穩度方面均有不同程度提升，在效率上均優于以上算法。

6 結論

在連續多段前瞻算法的基礎之上做了改進，提出了單段前瞻后顧算法；通過仿真實驗，對比分析了3種不同速度規劃算法的效率和平穩性。在同等條件下，單段直線前瞻后顧算法效率和平穩性更好，效率比無前瞻算法提高72.56%，比連續多段前瞻算法提高27.48%；柔性沖擊次數比無前瞻算法減少34.49%，比連續多段前瞻算僅多1次。此外，算法能夠在嵌入式數控系統平臺(STM32F407)上實現，測量結果與仿真吻合。