壓垮速度對周向MLEFP成型性能影響分析

苗潤源，程淑杰，梁安定，梁爭峰

(西安近代化學研究所， 西安 710065)

爆炸成型彈丸(explosively formed penetrators,EFP)具有更高的打擊比動能以及良好的氣動外形，大大提高了穿甲能力，可直接“擊爆”來襲目標的戰斗部，對于反厚壁類精確制導彈藥具有重要的意義[1-2]。周向MLEFP具有傳統EFP的優點外，同時也具有彈丸空間分布密度高的特點，成為近年來研究的熱點[3-5]。目前關于周向MLEFP的研究主要集中在總結藥型罩曲率半徑、壁厚、殼體等宏觀結構參數以及起爆方式等對周向MLEFP成型的影響規律，并且藥型罩結構大多采用球缺型藥型罩，而對于大錐角藥型罩微元壓垮速度的變化對周向MLEFP的成型影響規律研究較少[6-9]。基于上述原因，本文采用ANSYS/LS-DYNA顯式動力分析軟件對多個具有不同大錐角藥型罩結構參數的周向MLEFP的成型結果進行了數值模擬，并通過將彈丸成型結果與藥型罩微元壓垮速度進行結合對比分析，得到了藥型罩微元壓垮速度對周向MLEFP成型性能的影響規律[10-11]，并通過戰斗部試驗對所得到的結論進行驗證。該研究對于以后周向MLEFP戰斗部的設計可提供一定的指導。

1 數值模擬模型

1.1 模型組成及結構參數

建立如圖1所示的周向MLEFP數值模擬計算模型，在殼體圓周方向上通過預制刻槽的方式均勻分布18個藥型罩，每個藥型罩的結構參數均相同[12-13]，建模所采用的單位制為cm-g-μs。為減小數值模擬計算量，建立了1/4模型。

整個計算模型共分為3個PART，PART1為炸藥、PART2為空氣、PART3為藥型罩，其中炸藥材料選用高能混合炸藥，藥型罩材料選用純鐵。

該戰斗部的計算模型網絡總數：part1的網格總數為406 620個，part2的網格總數為302 670個，part3的網格總數為12 096個。

圖1 周向MLEFP數值模擬計算模型示意圖

圖2為藥型罩結構參數示意圖。其中D為戰斗部外徑，H為藥型罩高度，K為藥型罩頂點裝藥高度，δ1、δ2、R1、R2分別為藥型罩頂點厚度、邊緣厚度、內徑和外徑。

圖2 藥型罩結構示意圖

為研究藥型罩壓垮速度的變化對彈丸成型性能的影響，依次改變藥型罩曲率半徑、頂點及邊緣厚度比值、頂點裝填比，設計表1所示的4個方案藥型罩參數。所有藥型罩參數方案保持戰斗部外徑D、藥型罩高度H大小不變，并且H/D=0.5。

1.2 材料參數

使用顯式動力分析有限元程序ANSYS/LS-DYNA進行數值計算，為避免單元發生畸變影響計算過程，炸藥及空氣采用ALE算法，藥型罩采用拉格朗日算法，并通過關鍵字CONSTRINED_LAGRANGE_IN-SOLID進行流固耦合[14-15]。

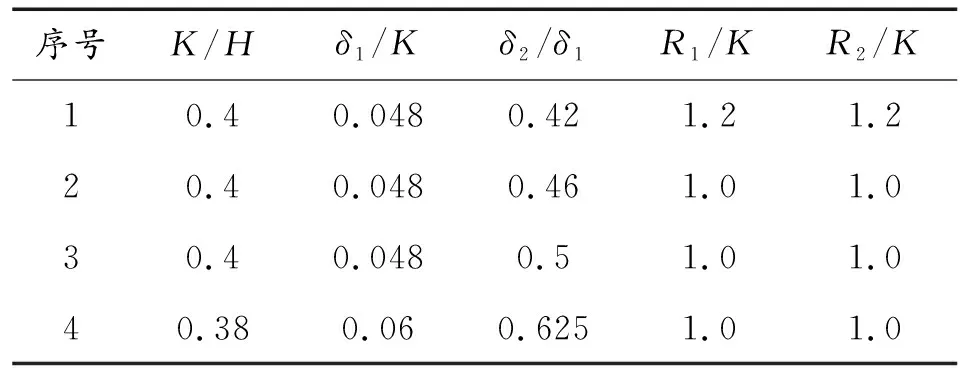
表1 藥型罩參數

藥型罩本構模型采用John-Cook本構模型，狀態方程為Gruneisen狀態方程，Gruneisen狀態方程表達式為：

(γ0+aμ)E

(1)

式(1)中:P為壓力;ρ0為初始密度；C為VS-VP曲線截距；S1、S2、S3為VS-VP曲線斜率系數；γ0為Gruneisenγ值；a為一階修正量。 對于純鐵材料，初始密度為7.85 g/cm3，剪切模量為0.77。

主裝藥本構模型為HIGH_EXPLOSIVE_BURN，狀態方程為JWL狀態方程，并且JWL狀態方程表達式為：

(2)

表2為JWL狀態方程相關參數值。

表2 JWL狀態方程參數

主裝藥采用的本構模型中，裝藥密度為1.78 g/cm3，爆速為8 200 m/s，CJ壓力為0.372 Mbar。

空氣采用EOS-LINEAR-POLYNOMIAL線性多項式狀態方程和MAT-NULL空材料模型，并且空氣密度為1.293×10-3g/cm3。

為保證彈丸成型過程中爆轟波的對稱性，起爆方式為戰斗部中心點起爆。

2 數值模擬結果及分析

2.1 數值模擬結果

對表1中4種采用不同藥型罩結構參數的周向MLEFP成型結果進行模擬，圖3(a)～圖3(d)分別為表1中4種彈丸最終成型結果。

由圖3彈丸成型結果可以看出，方案1中彈丸并未成型；方案2相比于方案1減小了曲率半徑，中彈丸頭部壓實，但長徑比較小；方案3相比于方案2增加了藥型罩邊緣厚度后，彈丸長徑比增加，成型效果較理想；方案4減小了藥型罩頂點裝填比，彈丸速度相比于方案3彈丸速度下降了15%，彈丸未成型。

圖3 周向MLEFP計算模型示意圖

2.2 數值模擬結果分析

分別選取每個方案中從藥型罩頂點到邊緣的10個微元，并得到每個微元壓垮速度的軸向及徑向分量。圖4、圖5分別為每個方案中藥型罩微元壓垮速度的軸向及徑向分量隨微元位置變化的分布曲線。

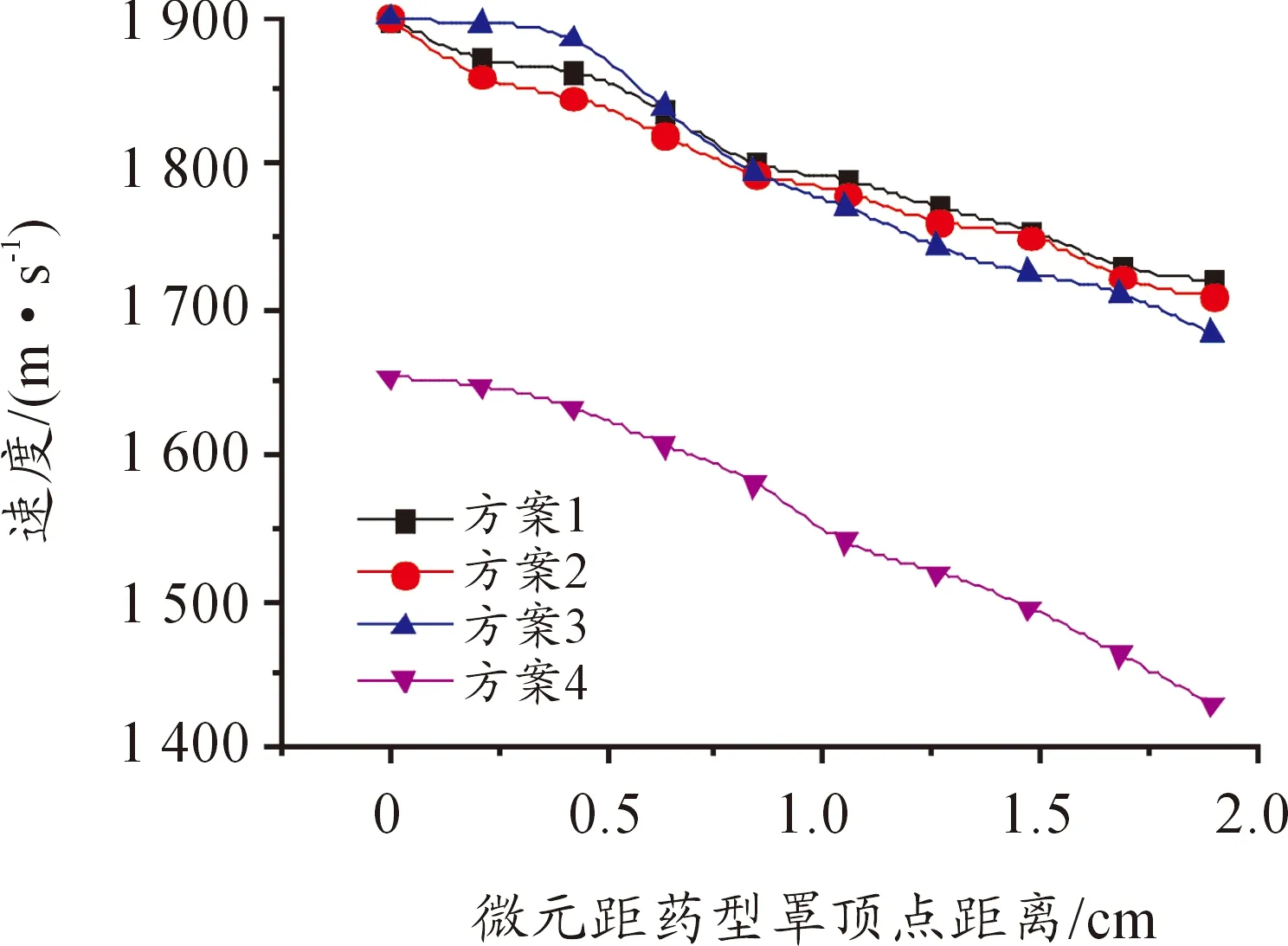
圖4 藥型罩微元壓垮速度軸向分量分布曲線

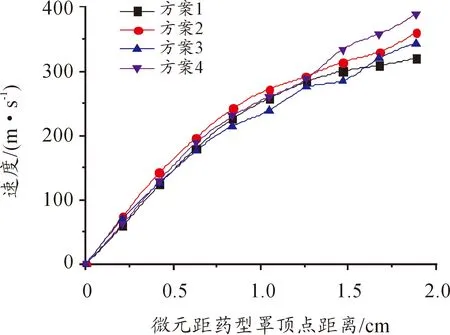
圖5 藥型罩微元壓垮速度徑向分量分布曲線

由圖4可以看出，方案1和2中藥型罩頂點及邊緣壓垮速度軸向差值均為180 m/s，彈丸成型結果均不理想；方案3中藥型罩頂點與邊緣的壓垮速度軸向差值達到了220 m/s，大于方案1和方案2中的藥型罩頂點與邊緣的軸向速度差，形成的彈丸長徑比最大，彈丸成型最理想；方案4中藥型罩頂點與邊緣壓垮速度軸向差值達到210 m/s，但由于藥型罩頂點壓垮速度軸向值相比于方案3，由1 900 m/s下降到1 650 m/s彈丸未成型。

由圖5可以看出，方案2中藥型罩微元壓垮速度徑向差值大于方案1中的差值，形成的彈丸頭部壓實，但長徑比太小。方案4藥型罩微元壓垮速度徑向差值最大，但由于藥型罩頂點壓垮速度軸向值太小，彈丸未成型。

以上數值模擬結果分析表明，藥型罩微元壓垮速度梯度與表1方案3中藥型罩微元壓垮速度梯度相同時，彈丸成型性能最好。

3 戰斗部試驗驗證

依據數值模擬所得到的結論，選取表1方案3中的參數作為周向MLEFP戰斗部藥型罩設計參數，設計如圖6所示的三層周向MLEFP戰斗部進行戰斗部毀傷性能試驗，藥型罩的材料為純鐵。

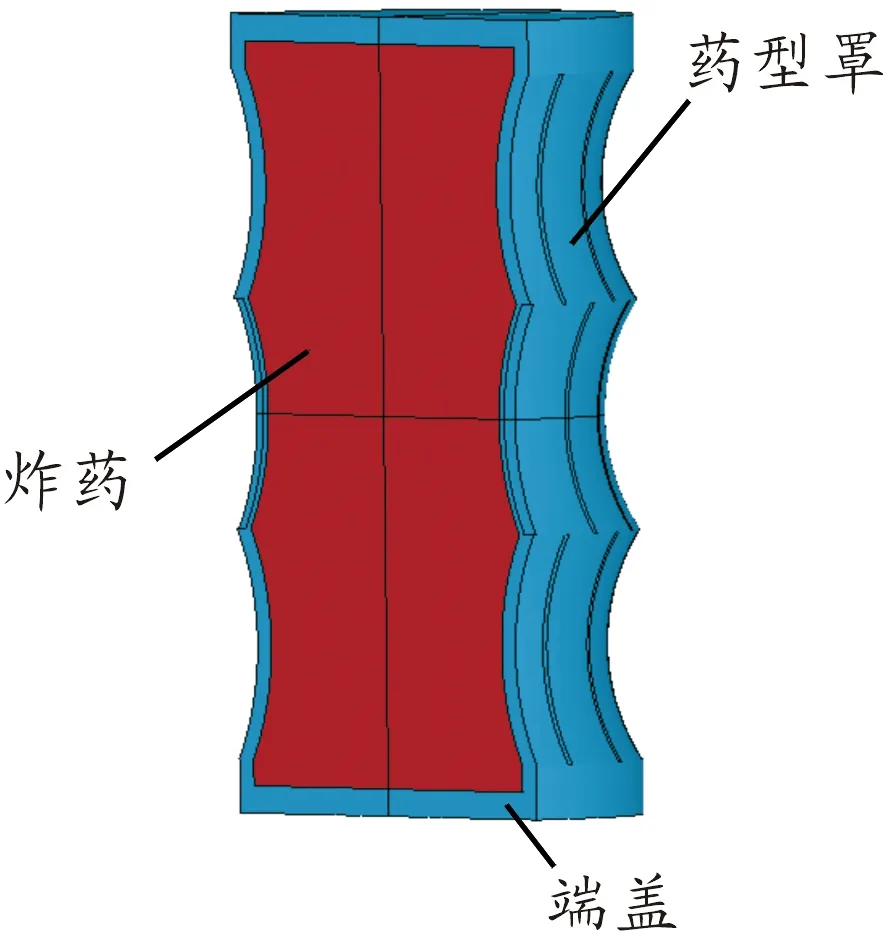
圖6 戰斗部結構示意圖

圖6中戰斗部藥型罩的材料為純鐵，主裝藥為高能熔鑄炸藥。

圖7為戰斗部靜爆試驗場布局照片，戰斗部豎直放置，距離戰斗部中心 6 m半徑處布置20 mm厚的Q235鋼板。引爆戰斗部后，通過統計彈丸對20 mm厚的Q235鋼板的穿甲率，對表1中F3彈丸成型性能進行驗證。

圖7 戰斗部靜爆試驗場布局照片

圖8為引爆戰斗部后，周向MLEFP在目標距離處的鋼板的穿孔分布圖。

圖8 周向MLEFP鋼板穿孔照片

依據試驗結果統計，周向MLEFP對6 m半徑處20 mm厚Q235鋼板的穿甲率為100%；靶板上彈丸穿孔的形狀大小基本與方案3中通過數值模擬得到的彈丸形狀一致，均為扁平狀。

以上試驗結果表明：當周向MLEFP初速不低于1 800 m/s且藥型罩頂點與邊緣壓跨速度軸向速度差值達到220 m/s時，周向MLEFP能夠成型性能良好，并能穩定飛行，具有很好的毀傷效果。

4 結論

1) 藥型罩頂點與邊緣壓垮速度軸向差值是彈丸成型的主要影響因素；增加藥型罩微元壓垮速度徑向差值有利于彈丸的壓合，但不利于增加彈丸的長徑比。

2) 對于藥型罩高度與戰斗部最大直徑比值為0.5的周向MLEFP，初速不低于1800 m/s時并且藥型罩頂點與邊緣的壓垮速度軸向差值達到220 m/s時，形成的彈丸長徑比大，能夠穩定飛行，并具有很好的毀傷效應。

3) 藥型罩頂點壓垮速度軸向值下降過多時，增加周向MLEFP成型時頂點與邊緣壓垮速度軸向差值有利于提高彈丸的成型性能。