一種人體運動機能非線性評價指標研究

張 霞,傅 豪,胡晉嘉,陳仁祥

(重慶交通大學 機電與車輛工程學院， 重慶 400074)

穿戴式機器人運動輔助過程中，通過獲取人體運動信息并有效識別出人體運動機能，有利于穿戴式機器人主/從運動控制的研究，為提高機器人的柔順運動輔助控制提供理論支撐[1]。根據研究方向不同，人體運動信息可分為4種：第一種是人體運動姿態的描述；第二種是描述人體運動時的力學參數，如受力情況、人體質心和速度等參數；第三種是人體運動時的生理信息，比如人體運動時肌肉收縮、放松變化產生的肌電信息；第四種是利用信息融合技術宏觀描述人體運動的協調性、平衡性等。由于表面肌電(surface electromyography，sEMG)信號變化與肌肉活動功能狀態之間存在良好的相關性，同時sEMG信號的獲取與分析也具有實時性、客觀性、敏感性和靈活性等特點[2]，因此在人體運動信息相關研究中，肌電信號具有天然的優勢。

根據研究對象和應用領域的不同，sEMG信號的研究主要分為三類：第一類是人的肢體動作的識別，該方法通過提取特征參數結合機器學習的算法對動作模式進行分類，達到識別人體動作的目的，廣泛應用于殘疾人的假肢控制領域[3-5]；第二類是肌肉疲勞及肌力的評價與判斷，sEMG信號的幅值一般和肌肉運動力度成正比，可以通過sEMG信號對肌力進行估算，文獻[6-8]利用信號的時頻分析技術，對遞增負荷下肌肉周期性動態疲勞進行估計，文獻[9]利用曲線擬合的方法建立了肌力預測模型，并考慮了疲勞狀態下的肌力；第三類是疾病機理的研究以及康復治療，例如對腦卒中、疼痛癥等疾病的分析，陳文敏、宋紅梅等[10-11]討論了身體疼痛與sEMG信號特征之間的關系。上述文獻表明：目前sEMG信號分析手段主要集中于時、頻域分析，時域特征指標有積分肌電值(integral Electromyographic，iEMG)、均方根值(Root Mean Square，RMS)和平均振幅(Mean Amplitude，MA)；頻域特征指標有平均功率頻率(Mean Power Frequency，MPF)和中位頻率(Median Frequency，MF)，普遍采用上述指標定性描述sEMG信號特征與肌肉疲勞與肌力狀態之間的關系[2]。由于sEMG信號實則是大量運動單元生物電活動在時間和空間上的非線性耦合，其特征非常復雜。傳統單一的評價指標與分析技術存在一定的局限性。因此迫切需要采用非線性分析的方法與技術開展sEMG信號非線性特征與運動機能狀態的相關性研究，進而挖掘出一種能有效評價運動機能的指標。

本文提出了一種基于分形維數標準差的人體運動機能非線性評價指標，采集人體下肢正常步行的sEMG信號進行預處理，再采用相空間重構和最大李雅普諾夫指數分析的方法，確定sEMG信號是一種混沌信號，進而采用計算分形維數的方法表征與運動機能密切相關的sEMG信號的復雜度，并提出分形維數標準差的評價指標用于評價持續運動過程中肌肉收縮、放松能力。通過對比分析運動能力存在差異的測試者的實驗數據，證明分形維數標準差的運動機能評價指標能夠有效表征不同個體的運動機能強弱，對穿戴式機器人的柔性運動控制提供理論依據。

1 sEMG信號采集與預處理

1.1 實驗設備

采用可穿戴式sEMG測量裝置Due-Pro進行肌電信號采集，其外觀如圖1所示。該設備有8個無線探頭最多可采集14個sEMG信號以及2個輔助信號(例如力、角度)，通過藍牙通信進行數據傳輸，并通過Matlab腳本程序進行數據保存供后期的數據處理。

圖1 Due-Pro采集裝置

1.2 實驗方案及信號預處理

本文選擇5名運動機能存在強弱差異、年齡為20～25歲且下肢步行正常的受試者，其中男性3名，愛好體育運動并有運動習慣；女性2名，沒有運動習慣，可以假設男、女測試者之間運動機能存在差異。設定受試者在運行速度為3 km/h的跑步機上步行，采集下肢右腿股直肌、股外側肌、股內側肌等八塊肌肉的sEMG信號。步行時長60 min，每間隔5 min采集1次信號，每幀時長1 min，采樣頻率為2 048 Hz，信號采集場景如圖2所示。

圖2 信號采集場景

采用中值濾波和帶通濾波的方法對sEMG信號進行預處理，濾波后各肌肉的sEMG信號如圖3所示。中值濾波中模板長度設為100，帶通濾波參數為通帶左邊界20 Hz、通帶右邊界50 Hz、衰減截止左邊界1 Hz、衰減截止右邊界500 Hz。

圖3 濾波后的sEMG信號場景圖

2 sEMG信號的非線性分析

2.1 sEMG信號的混沌性質

本文采用坐標延遲法對sEMG信號進行相空間重構，即根據時間序列{x(i)∶i=1,…,n}的不同延遲時間τ來確定維相空間空間矢量y(i)，矢量y(i)可表示為

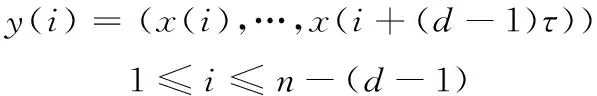
(1)

采用交互信息法計算τ，計算流程如下：

定義(S,Q)=(x(i),x(i+τ)),1≤i≤n-τ，也即S代表序列x(i)，Q代表序列x(i+τ)。則交互信息量I(S,Q)是關于延遲時間τ的函數，也記作I(τ)，I(τ)可表示為：

I(τ)=I(S,Q)=H(S)+H(Q)-H(S,Q)

(2)

式中H(S)與H(Q)分別為S與Q的熵，H(S,Q)為(S,Q)的共熵。計算出交互信息曲線I(τ)=I(S,Q)第一次達到極小值時的延遲時間就是最佳延遲時間，本文取延遲時間τ=16。

采用虛假最臨近點法計算嵌入維數d，即從最小嵌入維數2逐漸增加維數d，計算出處于當前維數下的虛假最臨近點所占比例，直到比例小于5%或者隨著維數的增加虛假最臨近點不再減小的時候，此時的維數就是嵌入維數，本文取嵌入維數d=2。

為了探討肌電信號是否為混沌信號，利用上述方法對sEMG信號、標準正弦周期信號及取值在[-1，1]的隨機信號進行相空間重構，計算結果如圖4所示。

圖4(a)、圖4(b)、圖4(c)分別顯示了sEMG信號、隨機信號和周期信號的相空間重構圖。區別于周期信號及隨機信號，sEMG信號的運動始終限于有限區域，軌跡永不重復并且形態復雜，其運動的復雜程度介于周期信號和隨機信號之間。這說明sEMG信號中的不穩定因素驅使狀態軌跡無限延伸，狀態軌跡在相空間中密集和遍歷，而穩定因素又將狀態軌跡限制在一定空間內，形成一定層次結構，具有明顯的伸長與折疊變換特點，結果表明sEMG信號具有混沌吸引子的典型特征，是混沌信號。

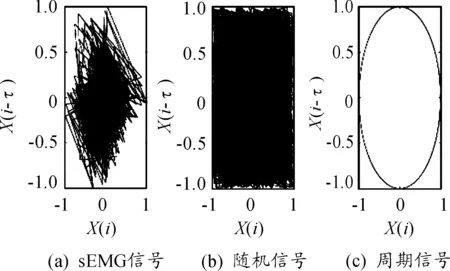
圖4 相空間重構圖

非線性動力系統在其相空間中的穩定狀態可以通過最大李雅普諾夫指數定量地描述出。本文再次通過計算最大李雅普諾夫指數來確定sEMG信號的混沌性，最大Lyapunov指數可由式(3)計算獲得：

(3)

式(3)中，L(tk)表示tk時刻最鄰近零點間的距離；M為計算總步數。不同的λmax對應于不同的運動狀態，各種運動形式及其對應的最大李雅普諾夫指數如表1所示。

表1 各種信號最大李雅普諾夫指數

分別截取五名測試者的RF(股直肌)sEMG信號，按上述方法計算最大李雅普洛夫指數值分別為：0.032 9、0.025 4、0.027 3、0.059 3和0.037 2。對比表1，sEMG信號的最大李雅普諾夫指數都處于0～∞的區間以內。該結果亦證明了sEMG信號為混沌信號，與前述分析結果一致。

2.2 sEMG信號的復雜度特征分析

肌肉收縮時，運動單元集中放電，信號成分較單一；肌肉放松時運動單元隨機放電，信號成分較復雜，因此，可認為sEMG信號復雜度與運動機能密切相關。本文采用計算分形維數的方法分析sEMG信號的復雜度特征，即利用分形維數表征信號的復雜度。采用“覆蓋分維”的思路計算sEMG信號的分形維數。由“覆蓋分維”定義，用大小為的盒子取覆蓋分形曲線，蓋完所必需的最少盒子數目為N(ε),計算分形維數D的公式如下：

(4)

為了證明分形維度與信號復雜度的相關性，本文通過合成不同占比的周期信號與隨機信號形成多個耦合信號，其中每一幀信號長度相同，利用上述方法逐個求取各耦合信號的分形維數，其結果如圖5所示。

圖5 不同信號對應的分形維數曲線

圖5的結果表明：耦合信號中的周期信號占比越大，隨機信號占比越小，信號中的復雜成分就越少，分形維數越小，反之。周期信號的占比趨近于100%時，信號的分形維數值趨近于1。因此可以得出分形維數越小，信號復雜度也就越小；反之，信號復雜度越大，分形維數與信號復雜度呈正相關。

表2為sEMG信號、周期信號、隨機信號的分形維數。周期信號的分形維數最小，其值趨近于1，信號的復雜度也最小；隨機信號的分形維數最大，信號的復雜度也是最大。而sEMG信號的分形維數介于周期信號與隨機信號之間，該結果說明采用分形維數表征信號復雜度的可行性。

表2 sEMG、周期、隨機信號的分形維數

2.3 分形維數標準差非線性指標

采用上述分形維數的計算方法計算下肢8塊肌肉的sEMG信號分形維數，研究了8塊肌肉的sEMG信號分形維數隨運動時間的變化規律。為了縮短計算時間并確保數據的可靠性，從步行運動5 min開始，每隔5 min分別截取5個步行周期、10個步行周期和15個步行周期的sEMG信號進行分形維數計算，其結果如圖6所示。

圖6顯示了在一個小時的步行運動過程中，各塊肌肉的sEMG信號分形維數的變化趨勢。從整體來看，各塊肌肉的分形維數隨著運動時間的增長并沒有明顯的變化。同時，從圖中可以看出5個步行周期、10個步行周期和15個步行周期的分形維數變化趨勢基本一致，反映出步行運動中的sEMG信號分形維數變化比較平緩，由此可見分形維數反映了人體固有運動機能特征，與運動時間及肌肉疲勞無關。

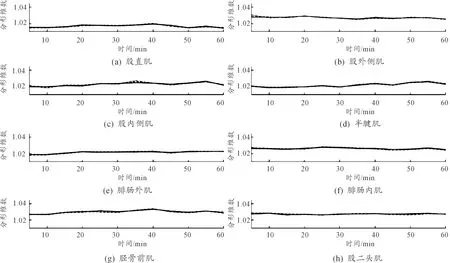
圖6 分形維數隨運動時間的變化趨勢曲線

本文分別計算某一受試者肌肉收縮和放松時的分形維數，原始sEMG信號及其分形維數如圖7所示。圖7(a)代表sEMG信號，圖7(b)代表sEMG信號對應的分形維數。

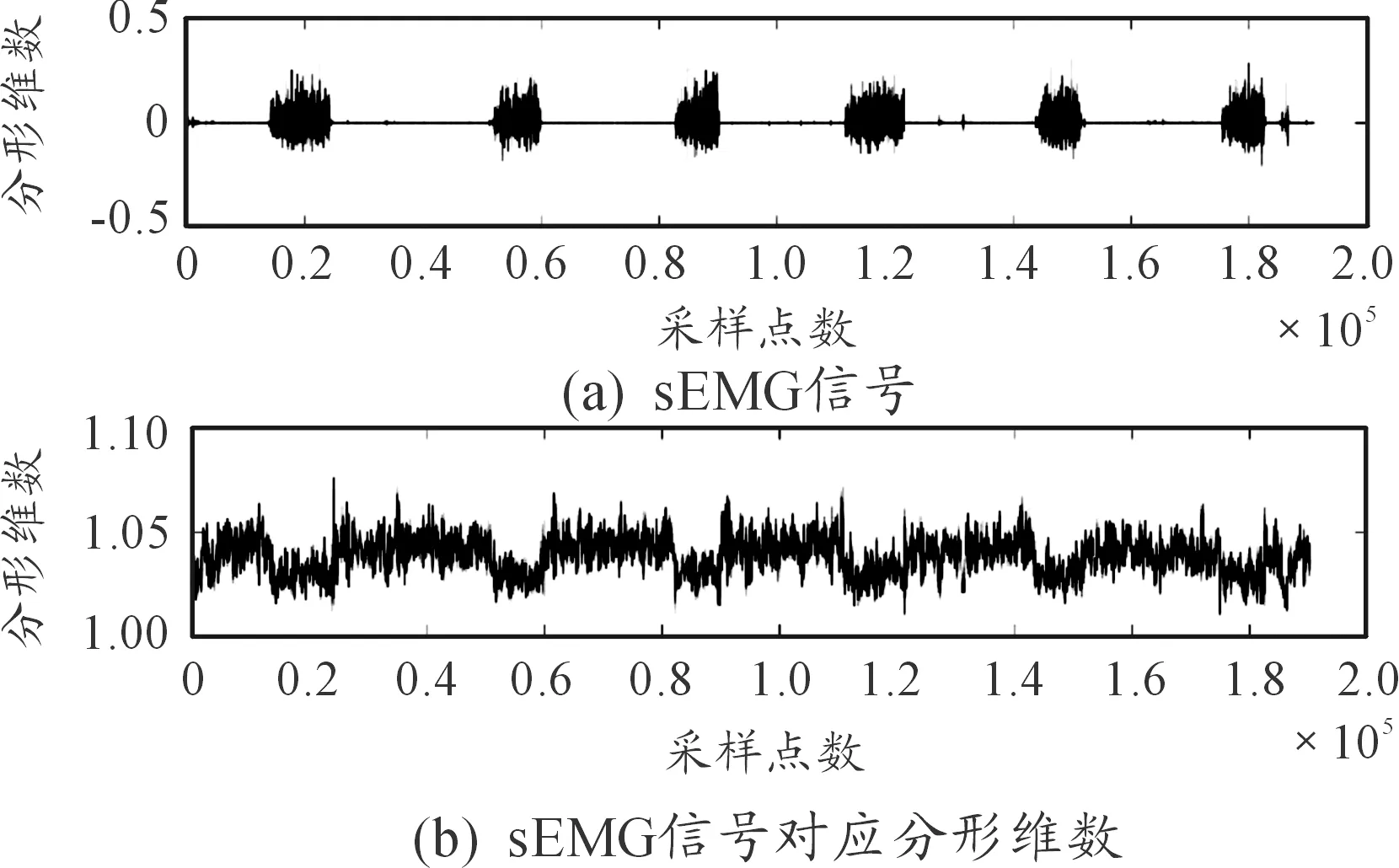
圖7 肌肉收縮和放松的分形維數曲線

從圖7可以看出：當肌肉收縮時sEMG信號的分形維數變小，信號的復雜度低；放松時分形維數變大，信號復雜度高，這是由于肌肉放松時肌肉纖維隨機放電，肌肉收縮時肌肉纖維協同放電。并且人體肌肉的收縮能力越強，肌纖維放電越集中，收縮時的sEMG信號成分也越單一；而當肌肉放松時候則恰恰相反，肌肉的放松能力越強，放松時的sEMG信號成分越復雜。本文進一步統計了5名受試者肌肉靜態收縮-放松時的sEMG信號分形維數，其結果如表3所示。表3結果表明，所有測試者在肌肉收縮時，分形維數較小，而在肌肉放松時，分形維數較大。總而言之，人體運動機能越強，其放松時sEMG信號分形維數越大而收縮時sEMG信號的分形維數越小。該研究結果表明測試者個體肌肉收縮-放松能力與收縮-放松時sEMG信號的分形維數差值有關。

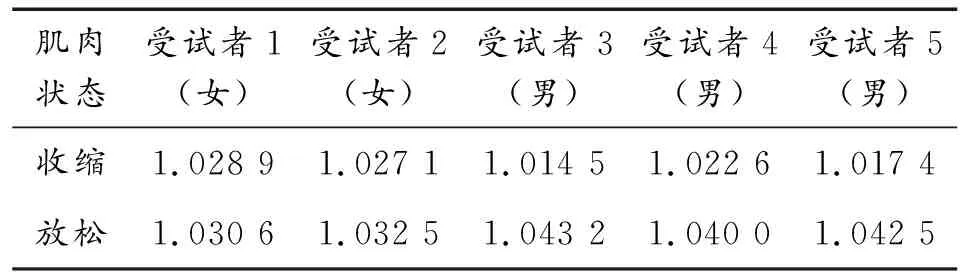
表3 5名受試者肌肉靜態收縮、放松的分形維數

為了評價持續運動過程中肌肉收縮-放松能力，本文進一步取數個周期sEMG信號分形維數的標準差，基于上述分析結果，假設分形維數的標準差越大，則肌肉收縮-放松時sEMG信號分形維數變化差異越大，肌肉收縮-放松的能力也就越強，運動機能越強。

進一步對比分析了2對4名測試者的數據。各測試者股直肌sEMG信號及其分形維數曲線如圖8所示。從圖8可以看出：男性測試者的肌肉收縮更加快速集中，sEMG信號整體表現出的肌肉收縮、放松規律也更強。計算出男性測試者1、2的分形維數標準差分別為0.010 7、0.008 5，女性測試者1、2的分形維數標準差分別為0.007 7、0.005 1。男性測試者的分形維數標準差比女性測試者的分形維數標準差大，則男性測試者的股直肌收縮-放松能力比女性測試者強，因此男性測試者運動機能比女性測試者強。

進一步對比分析5名測試者8塊肌肉在持續運動下的數據，各肌肉sEMG信號的分形維數標準差如圖9所示。從圖9可以得出：同一塊肌肉不同測試者的分形維數標準差存在大小差異，則不同測試者的同一塊肌肉運動機能也存在強弱差異。該結果表明測試者個體肌肉收縮-放松時sEMG信號的分形維數標準差的差值與運動機能強弱有關。綜上分析，本文所提出的分形維數標準差非線性指標能夠有效評價不同個體的運動機能。

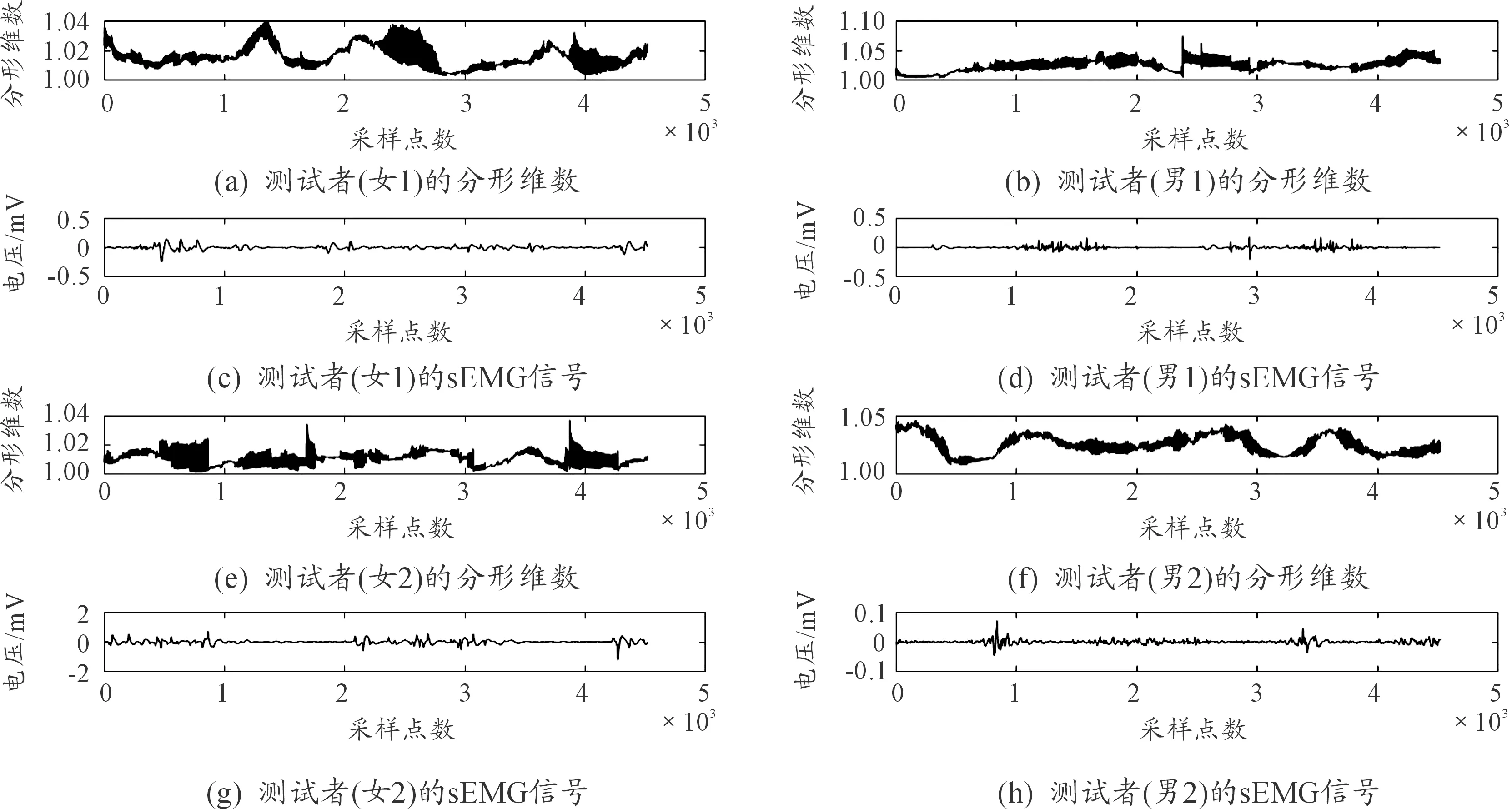
圖8 不同受試者步行運動的sEMG信號及其分形維數曲線

圖9 各肌肉分形維數標準差圖

3 結論

對人體下肢正常步行的sEMG信號進行非線性分析，提出一種新的基于分形維數標準差的運動機能評價指標。采用相空間重構圖和最大李雅普諾夫指數確定sEMG信號是一種混沌信號，由混沌信號的自相似性進而計算分形維數表征與運動機能密切相關的sEMG信號的復雜度，得出個體肌肉收縮-放松能力與其sEMG信號分形維數差值有關。為了評價人體在持續運動過程中肌肉收縮和放松能力，提出分形維數標準差非線性評價指標。通過對具有不同運動機能、共5位受試者的數據進行對比分析，證明分形維數標準差與肌肉收縮-放松能力的正相關性。本文提出的非線性指標能有效表征不同個體運動機能的強弱，可為穿戴式機器人的柔性運動控制實踐提供理論依據。