基于BP神經網絡的某反裝甲武器系統打擊效果預測
遲明祎,侯興明,陳小衛,周 瑜
(1.航天工程大學 航天保障系, 北京 102200; 2.中國解放軍63850部隊, 吉林 白城 137001;3.中國解放軍32183部隊, 遼寧 錦州 121000)
在作戰模擬和計劃制定、作戰試驗方案設計的過程中,火力打擊效果的預估是預測體系作戰效能的關鍵,是合理配置作戰資源、正確組織火力毀傷行動的依據[1],也是作戰試驗方案評估的重要方法。
現代陸地戰爭不斷發展變化,便攜式反裝甲武器經過了半個多世紀“四代”的發展,戰術技術性能明顯提升,已經成為戰場上抵擋裝甲機械化步兵團突擊的尖端利器[2]。反裝甲武器誕生時間長,作戰和演訓中的應用場景較多,隨著便攜式反裝甲武器系統的智能化程度的提升,彈丸的造價也越來越高,考慮到試驗成本和周期問題,在試驗階段不可能將所有的影響因子任意組合設計試驗科目以得到所有因子組合場景下的試驗結果。立足靶場已經積累的試驗數據,設計一種火力打擊效果預測模型,預測各個影響因子在不同組合情況下反裝甲武器的打擊效果,從而輔助指揮員決策,為作戰籌劃服務很有必要。
當前關于對武器系統打擊效果的預測方法,主要有專家評議法、統計分析法、數學解析法等[3-4]。然而,專家評議法過多依賴專家的經驗素質和推理能力,主觀因素較多;統計分析法需要分析大量的數據進行歸納總結,當影響因子較多且之間關系極為復雜時,統計分析方法很難實施;數學解析法不能避開打擊效果與影響因子之間復雜的機理關系的分析[1,3,5-8]。上述方法在處理反裝甲武器系統打擊效果預測問題上均存在缺陷。
近年來,隨著神經網絡、機器學習和人工智能的迅猛發展,神經網絡方法已經開始逐漸運用于軍事領域問題的分析,作為一種“黑箱”模型算法,神經網絡具有很強的容錯和自學習能力[6]。而基于梯度下降法的3層BP神經網絡在解決復雜非線性問題方面非常有優勢[3]。來自印度共生國際大學的學者L.V.Kamble[9]在文章中運用了梯度法向傳播的神經網絡模型用于模擬水平管在大顆粒氣固流化床中的傳熱預測,預測結果與實驗值非常吻合。來自Mahakal理工學院機械工程系的學者Shrikant Pandey[10]借助人工神經網絡(ANN)預測室內溫度,使用實驗數據作為訓練樣本,運用traingdm,traingdx,trainrp等多種訓練算法訓練模型,經比對發現traingdx梯度下降法這種方法具有計算速度快,通過自適應學習逐步提高性能,自組織和實時的優點。劉芳等[4]指出,部分學者將一般神經網絡和支持向量機運用于預測分析中,但是會出現訓練神經網絡訓練速度慢,易陷入局部最小解的問題以及支持向量機對缺失數據的極度敏感問題。譚麗萍等[6]借助基于traingdx函數梯度下降法的三層BP神經網絡解決GNSS高斯擬合問題,得出選用 traingdx 梯度下降訓練法作為訓練函數,效果最佳,擬合精度好于其他訓練函數的結論。
根據上述觀點,本文根據反裝甲武器打擊效果與因素間的復雜關系特性,神經網絡的功能特性,采用基于改進的融合小波函數梯度下降法BP神經網絡構建預測模型,避開對系統內部復雜的機理和關系的分析[1],直接借助以往作戰試驗產生的數據樣本對模型進行訓練,通過反復修正,確定網絡結構和參數,實現對某型反裝甲武器系統的打擊效果的預測,從而為指揮員的決策部署、作戰籌劃和試驗方案設計的評估提供依據。
1 反裝甲武器系統打擊效果影響因子分析
以射程對打擊效果的影響為例,選取兩種情況下射擊科目的試驗數據生成打擊效果隨射程變化的曲線,確保在每組數據中射程為唯一變量。
從圖1可以看出:在不同條件下,打擊效果的量值有差異,且曲線的變化趨勢也不相同;即使在同等條件下,打擊效果隨射程增加呈非呈線性變化。通過分析將可能的原因歸結如下:
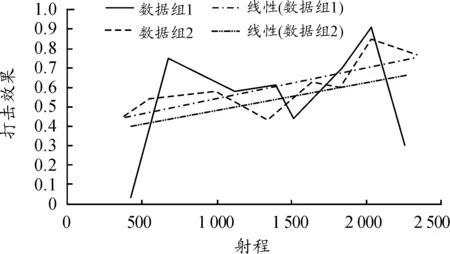
圖1 打擊效果隨射程變化曲線
1) 在一定范圍內射程增加會增加彈丸的動量,對打擊效果呈正向作用;
2) 在一定的范圍內射程的變化會導致彈道末段彈丸速度變化,從而導致炸點與靶面的距離的變化,導致打擊效果變化;
3) 在一定范圍內射程的變化,彈丸飛行期間靶車會產生位移,導致彈丸中靶或空爆時的入射姿態發生變化,從而導致打擊效果發生變化;
4) 射程的變化還會對其他的影響因子如超壓峰值、正壓作用時間產生影響,共同作用于打擊效果。
通過對歷史數據的分析可知,裝甲目標的打擊效果與其影響因素之間呈十分復雜的非線性關系,各因素對目標的打擊效果的影響大小和方向各不相同。為了解決反裝甲武器系統打擊效果的預測問題,首先要確定反裝甲武器系統打擊效果的影響因子有哪些。
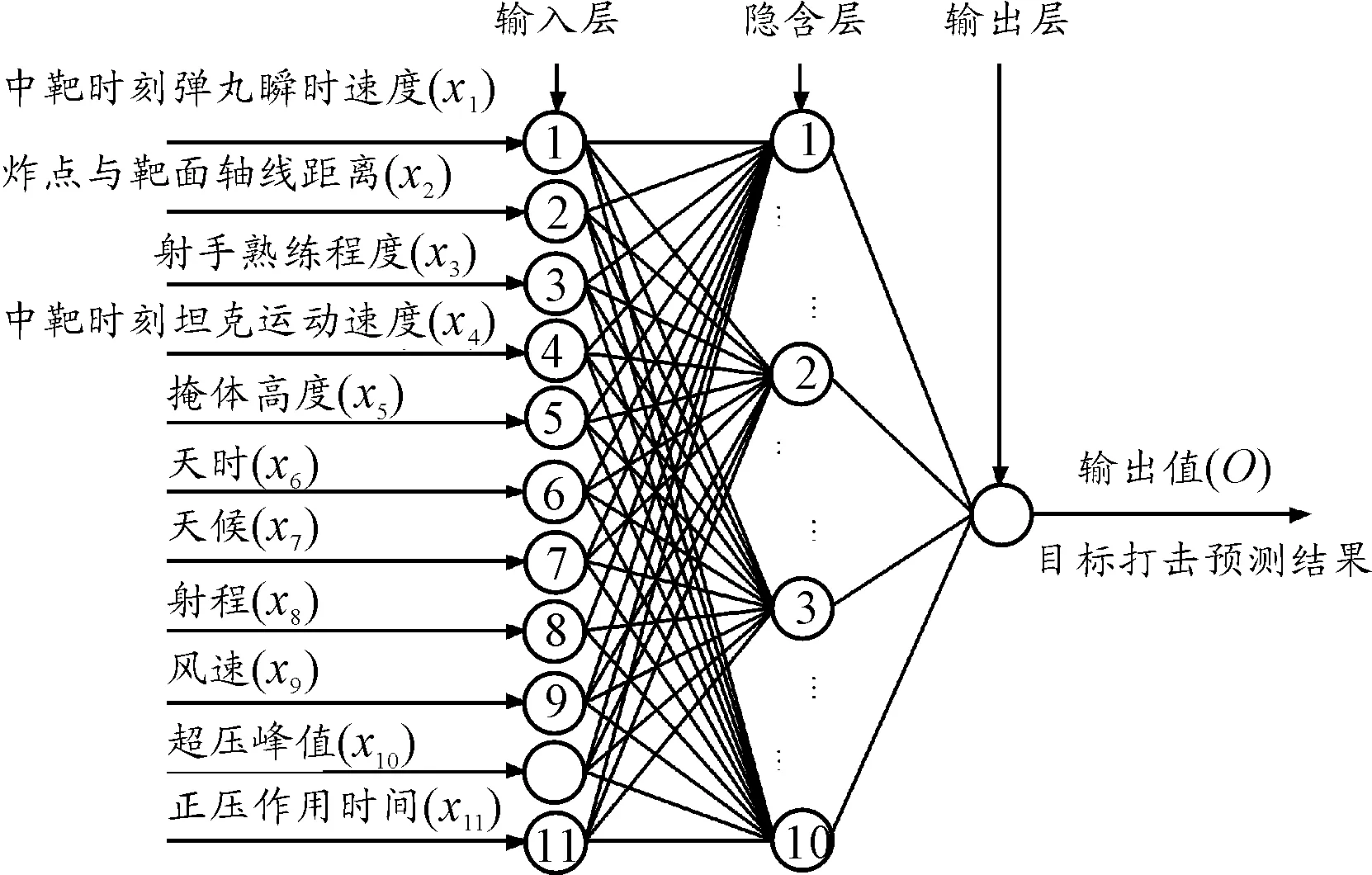
在近幾年的高機動步兵營反裝甲火力運用能力試驗中,數據采集技術人員伴隨采集有關參數達三十多種,其中只有部分因素對反裝甲武器打擊效果產生影響,且其影響大小和方向也各不相同。構建模型時影響因子過多會使模型結構復雜化,增加模型實現的難度,因子有遺漏會導致模型預測不準。結合Delphi專家評議法、部隊調研、試驗部隊操作經驗、試驗保障人員的經驗判斷以及繪制分析單個因子對打擊效果的影響曲線等方法,經過反復的分析和實驗(當影響因子選取有遺漏時,可能造成神經網絡不收斂),得出反裝甲武器系統的十一個影響因子如下:中靶時刻彈丸瞬時速度(m),炸點與靶面軸線距離(m),中靶時刻目標運動速度(m/s),掩體高度(m),射程(m),沖擊波強度(kPa),正壓作用時間(s),射手熟練程度(按九等級劃分法分為極差、差、較差、不合格、合格、較好、良、優良、優并分配量值區間)。自然環境條件3個:天時(按晝夜賦值量化),天候(按光照強度分級量化),風速(m/s)。
首先進行部分數據的量化和歸一化的預處理。對于定性指標的量化,如射手熟練程度指標,按照經典的標度對照法,劃分極差、差、較差、不合格、合格、較好、良、優良、優,對應0.1、0.2、…、0.8、0.9[12]。定量指標的常用的規范化方法有標準化法,比重法與閾值法[13]。比重法的優勢在于經變換之后較客觀反映原始指標間的關系,考慮了指標值間的差異性,前提是所有量化指標都滿足xi≥0[14]。本文采用比重法進行規范化處理的方法如下[14]:
(1)
其中:xi為第i個樣本數據;yi為規范化后的值。
2 模型構建
一般認為,神經網絡結構越復雜,層數越多,節點數越多,模型往往具有更好網絡性能和泛化能力,但是缺點是相應會增加運算量,增加實現的難度,所以選擇適合于反裝甲武器系統的打擊效果預測的神經網絡模型是關鍵。一般首選3層網絡,即只含有一個隱層的神經網絡,可適當調整隱含層的神經節點數,增加隱層節點數要比增加隱層數更容易實現[1,11,13]。在理論上已經證明,一個包含一個隱含層的3層神經網絡可以以任意的精度逼近任意一個非線性函數,前提是隱含層的神經元數可以任意調整[1,15]。
2.1 基于BP神經網絡的反裝甲武器打擊效果預測模型算法流程
BP神經網絡(Back-ProPagation Network)是一種信號沿正方向單向傳播而誤差經過反饋沿反向傳播的神經網絡,擁有輸入層、至少一個隱含層和輸出層的多層網絡[6]。BP學習算法是多級非循環的訓練算法,其基本思想是利用最小二乘法和梯度搜索技術,以期使網絡的實際輸出與期望輸出之間的誤差均方差為最小,網絡學習過程是一個誤差邊傳播邊修正網絡參數的過程。根據BP神經網絡的理論原理和問題特性,基于BP神經網絡的反裝甲武器打擊效果預測模型的算法流程如圖2所示。
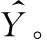
步驟2:設置神經元間連接權系數和神經元閾值初始值。對神經元間連接權系數和神經元閾值進行初始化,隨機取[-1,1]之間的值(其中權重極值1表示正相關,-1表示負相關),所有節點參數的變化量和學習率變化量初始化為0,設置初始學習率初始值和誤差容許值Rallow。
步驟3:計算第t次迭代隱含層和輸出層的輸出值。信息沿著神經網絡節點間的通路由輸入層向輸出層逐層正向傳輸,計算各層的輸出值Oj,j表示第j個節點:
(2)
假設相鄰兩層節點之間一一連接,同層節點之間無連接。其中,n表示節點j的輸入節點數,xi是第i個輸入節點的輸出值,神經網絡中輸入層的輸入到輸出一般不做運算所以xi等于Xi,wji是輸入層第i個節點到下一層第j個節點的連接權系數值,θj表示閾值。神經元節點連接關系如圖3所示。

圖3 神經元節點連接關系示意圖

(3)
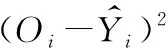
wji(t+1)=wji(t)+ηδjoj+a[wji(t)-wji(t-1)]
(4)
θj(t+1)=θj(t)+aδj
(5)
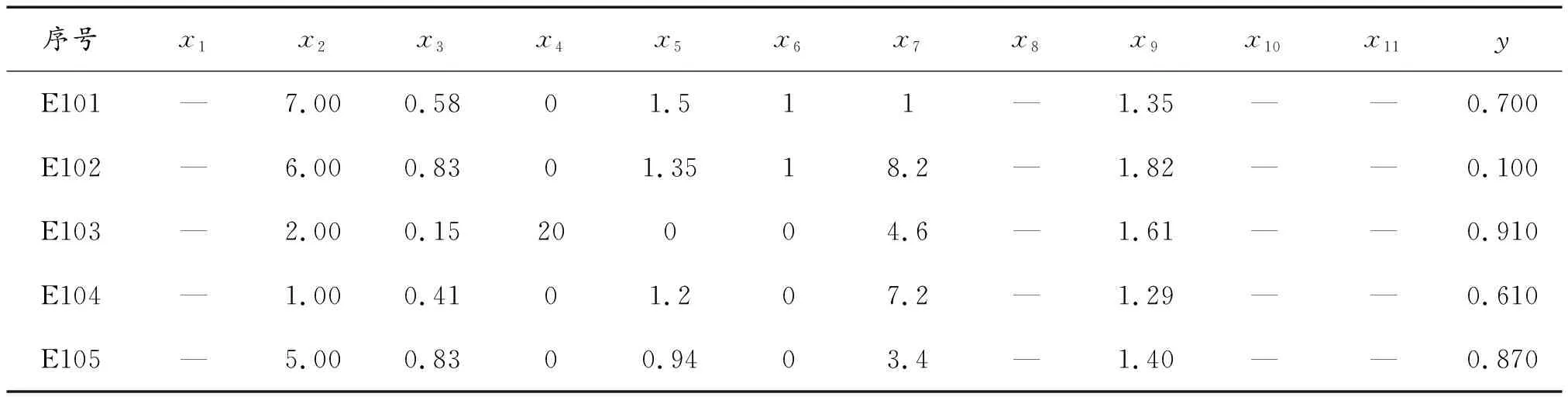
其中:t、t+1,t-1表示該迭代次序;η是學習系數(也稱為學習步長,0<η<1);a是沖量系數(0 1) 如果節點j在輸出層,遵循: (6) 2) 如果節點j不在輸出層,在其他各隱含層,因沒有期望輸出值,無法進行輸出值比較,則遵循: (7) 式(7)中,假設j層的輸出節點總數為k。 轉到步驟3進行第t+1次循環計算。 步驟5:訓練結束,用某次試驗數據檢驗神經網絡的訓練效果,對火力打擊效果的量值進行預測。 上述預測算法流程是一個迭代過程。每一輪執行中將連接各權系數值和閾值調整一次,進入下一次計算,迭代循環進行下去,直到期望輸出與計算輸出的均方差小于預設的容許值,學習訓練階段結束,模型形成較好的包絡,預測模型建立。 本例中,輸入層神經元個數為11,輸出層節點數為1,則根據BP神經網絡隱含層設計經驗公式[17]: (8) 式(8)中:mhidden表示隱含層節點數;nin表示輸入層節點數;lout表示輸出層節點數;h為1~10之間的整數。 考慮本文所研究的問題的實際情況,經過反復嘗試驗證,最終確定隱含層神經節點個數為10,即形成了具有11-10-1網絡結構的某型反裝甲武器系統目標打擊效果BP神經網絡預測模型,如圖4所示。 BP神經網絡預測結果的準確性主要受網絡結構、樣本的代表性與訓練函數選取三方面的影響[18]。選取不同的訓練函數,訓練的速度和樣本擬合的精度不同。為了減小局部最小解出現的可能,在各種訓練函數中,Matlab軟件中的traingdx函數的精度效果比較好,故選取traingdx作為神經網絡隱含層訓練函數。traingdx函數是一種帶沖量(momentum)的并且具有自適應學習速率(lr,learning rate)的梯度下降算法函數[4],通常用來解決在隱含層神經節點數較少的情況下的擬合問題。 圖4 11-10-1結構的BP神經網絡預測模型示意圖 采用小波函數作為隱含層神經元的激勵函數,可增加神經網絡結構的學習功能[19],提高模型的訓練效率,同時可降低局部最小解出現的情況。輸出節點的激勵函數通常是非線性可微的,常采用Sigmoid函數作為輸出層神經元激勵函數。Sigmoid函數的表達式如下[20]: Sigmoid函數: (9) 神經網絡的輸出輸入關系表達式如下: (10) (11) 至此,火力打擊效果預測神經網絡模型的迭代在于求解模型參數,即包括尺度變量aj、平移變量bj、輸入層到隱含層的連接權系數、閾值、隱含層到輸出層的連接權系數v1j、 閾值λij。基本數學方程如下: (12) BP神經網絡預測結果的準確性主要受網絡結構、樣本的代表性與訓練函數選取三方面的影響[18]。在近幾年開展的歷次作戰試驗產生的大量的歷史數據樣本中,選取底層參量和輸出量值均勻分布的并且具有代表性的105組數據作為本模型的訓練樣本,在算法中首先進行了數據的量化和歸一化的預處理。其中,部分訓練樣本中原始數據如表1所示。 表1 打擊效果預測模型訓練樣本原始數據 將第1~105組數據作為訓練樣本輸入模型,設置訓練允許誤差Rallow為0.01,最大迭代次數為1 000。用Matlab軟件進行訓練,輸出誤差隨迭代次數的變化曲線如圖5所示。 圖5 基于Matlab軟件的訓練誤差隨迭代次數變化曲線 由圖5可以看出:當大約進行300次訓練時,輸出誤差達到最小。將反裝甲火力運用能力試驗實測的歷史數據挑選第106~113共8組數據作為檢驗樣本,輸入預測模型,將打擊效果的預測值和真實值作比對,對比結果如表2所示。 借助平均絕對百分比誤差(MAPE)對預測效果進行評價,其計算公式如下[21]: (13) 表2 神經網絡模型預測結果 通過對某型反裝甲武器系統打擊效果影響因子分析基礎上,運用融合小波函數的改進的梯度下降法BP神經網絡仿真建模技術,構建影響因素和打擊效果量值之間的關系模型,借助歷史試驗數據樣本對模型進行訓練。借助新的歷史試驗數據對模型的預測效果進行檢驗,通過數據對比結果可以看出,該預測模型預測性較好。通過建立基于改進的梯度下降法BP神經網絡的預測模型,可實現對該武器系統打擊效果有效預測,可為火力打擊方案擬制、試驗方案評估和武器裝備性能改進提供科學依據,也為海量作戰試驗數據的分析、挖掘和再利用提供了思路。

2.2 BP神經網絡預測模型結構設計
2.3 BP神經網絡預測模型訓練函數選取
2.4 BP神經網絡預測模型激勵函數的改進


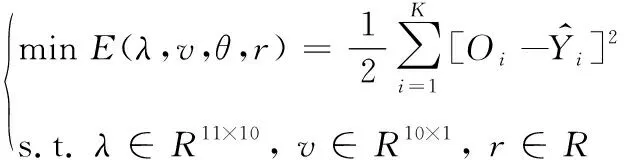
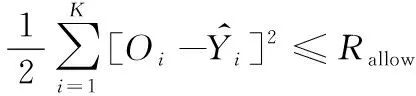
3 算例分析



4 結論

