基于實測過載的彈體侵徹姿態(tài)角計算模型

張銥翔，牛少華，唐 彬，陶逢剛，孫遠程，劉天國

(1.北京理工大學 機電學院， 北京 100081；2.中國工程物理研究院 電子工程研究所， 四川 綿陽 621999)

對高價值硬目標的精確打擊和高效毀傷，在現代戰(zhàn)爭中起著越來越重要的作用。為了實現對目標的最佳毀傷效果，要求侵徹彈引信能夠實時有效地對侵徹過程進行識別和判斷，并采取相應的策略對彈藥進行控制和起爆[1-2]。彈體在侵徹過程中，由于受到目標的作用，其姿態(tài)會發(fā)生變化。彈體侵徹姿態(tài)變化一方面會影響對侵徹信息的識別，另一方面則會對其侵徹能力產生影響。目前，關于對彈體侵徹機理及炸藥控制方面的研究較多[3-6]，而在彈體侵徹姿態(tài)識別方面的研究相對較少。彈體飛行姿態(tài)的識別，在彈體導引系統和引信系統中通常可采用由陀螺和加速度傳感器構成慣性測量單元來實現，李慧[7]采用磁強計、加速度計和陀螺復合系統進行測量，曹紅松等[8]利用地磁矢量和陀螺探測結果解算彈體姿態(tài),杜燁等[9]采用二軸磁強計和MEMS陀螺對彈箭進行測量，但是對于高速侵徹彈藥，在侵徹目標過程中，彈體及內部結構將經歷極其惡劣的高沖擊過載環(huán)境的作用,而目前已有的陀螺無法適應這種環(huán)境，因此研究基于加速度傳感器獲取的侵徹過載計算得到彈體的侵徹姿態(tài)具有十分重要的工程意義。張建新等[10]研究了基于兩個三軸加速度傳感器軌跡計算方法，但存在一定的不足之處，該方法中將傳感器測得的加速度默認為是靶板坐標系下的加速度。但實際上，由于加速度傳感器是安裝于彈體引信內，其實測得到的加速度實際上是彈體自身運動坐標系下的加速度，因此，研究基于加速度傳感器實時測得的過載計算得到彈體侵徹姿態(tài)很有必要，也具有更好的工程實用價值。

1 彈體運動坐標與靶板固定坐標

在彈體侵徹靶板過程中，靶板相對地面是固定的，彈體相對地面是運動的，為研究彈體相對靶板的侵徹姿態(tài)，建立如圖1所示的坐標系，其中OXYZ是以靶板為參考系的固定坐標系,O′X′Y′Z′、O″X″Y″Z″、O?X?Y?Z?是基于彈體自身建立的運動坐標系，彈體沿v0方向撞擊靶板。t0時刻彈體運動坐標系O′X′Y′Z′與靶板固定坐標系OXYZ方向一致，撞擊靶板后，彈體姿態(tài)可能會發(fā)生改變。根據彈體姿態(tài)變化可分為A、B兩種情況。對于A情況，彈體姿態(tài)變化較小，彈體運動坐標系O″X″Y″Z″與O′X′Y′Z′的角度變化也較小，彈體在OXYZ坐標系中Z向承受的過載較大，在坐標系O′X′Y′Z′中Z′向承受的過載較大，X′、Y′向承受的過載較小；對于B情況，彈體姿態(tài)變化很大，彈體運動坐標系O?X?Y?Z?與O′X′Y′Z′的角度變化很大，彈體在OXYZ坐標系中Z向承受的過載較大，在坐標系O′X′Y′Z′中Y?向承受的過載較大，X?、Z?向承受的過載較小。由于加速度傳感器是固定于彈體內，其測得的是沿彈體軸向和徑向過載，若將傳感器測得的加速度等同于固定坐標系下的加速度來計算彈體姿態(tài)，則會產生較大的誤差，因此研究基于加速度傳感器實時測得的加速度計算得到彈體侵徹姿態(tài)很有必要。

圖1 彈體運動坐標系與靶板固定坐標系

2 彈體實時侵徹姿態(tài)

彈體侵徹過程中，三維加速度傳感器測得的軸向加速度az(t)，徑向加速度ax(t)，ay(t)，加速度方向分別與運動坐標系的坐標軸一致。

式中：vz(t)為t時刻運動坐標系下的彈體軸向速度，vx(t)、vy(t)為t時刻運動坐標系下的彈體徑向速度，z(t)為t時刻運動坐標系下的彈體軸向位移，x(t)、y(t)為t時刻運動坐標系下的彈體徑向位移。

在彈體實際的侵徹過程中，需要對三軸加速度傳感器的過載信號進行實時處理，此時二次積分從0時刻到t時刻的過載信息將無法保證計算的時效性。

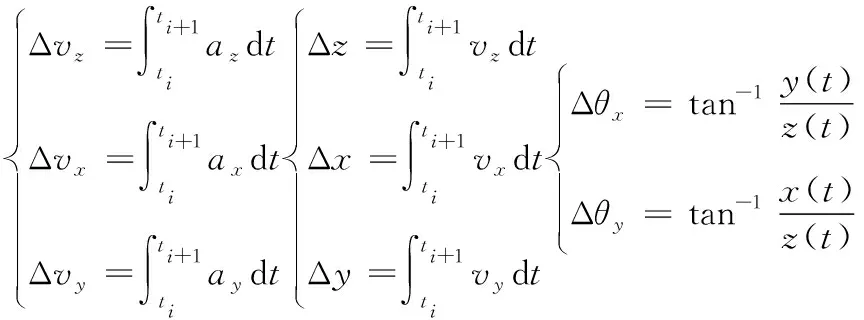
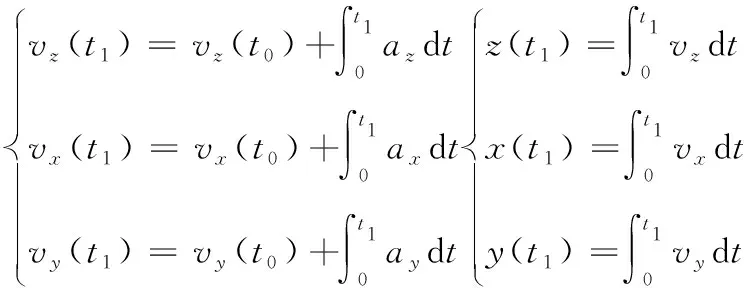
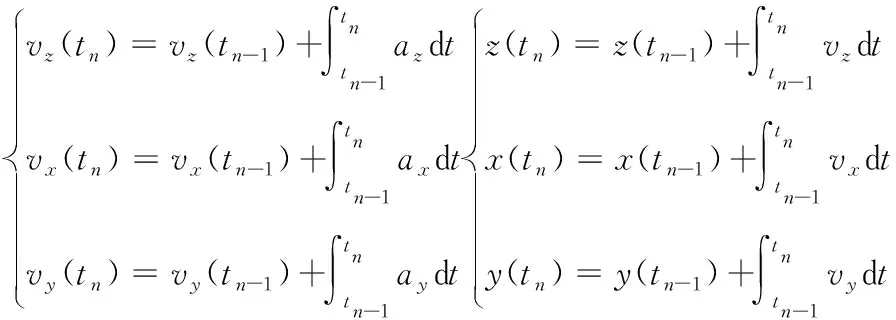
在實時計算過程中，每一時刻進行一次速度、位移、角度變化以及姿態(tài)角的計算，將前一時刻的結果與變化量進行疊加得到新的結果。

3 數值仿真及結果分析

在彈體實際侵徹過程中，加速度傳感器無法得到彈體的姿態(tài)角變化曲線，因此選用數值仿真方法對一工況進行仿真，將仿真所得過載信息通過坐標系變換得到傳感器實測過載信息，并進行姿態(tài)角計算，將計算結果與仿真結果進行對比。

采用有限元動力學軟件LS-DYNA對彈體斜侵徹多層加筋鋼靶板進行數值仿真，彈體采用各向同性彈塑性模型(*MAT_PLASTIC_KINEMATIC),靶體采用Johnson-Cook材料模型(*MAT_JOHNOSN_COOK)以及Gruneisen狀態(tài)方程(*EOS_GRUNEISEN),彈體和靶板分別為G50鋼和922A(10CrNi2MoCu)鋼，材料參數分別見表1、表2。彈體為φ400 mm×1 300 mm的截卵型彈體，頭部長560 mm，卵型半徑為1 000 mm，靶板為含T型加強筋的均質靶板，彈體初始速度為1 200 m/s，計算時間步長為10 μs。通過數值仿真可以得到三軸加速度傳感器在靶板固定坐標系下的軸向加速度以及徑向加速度，如圖2所示。

表1 彈體材料參數

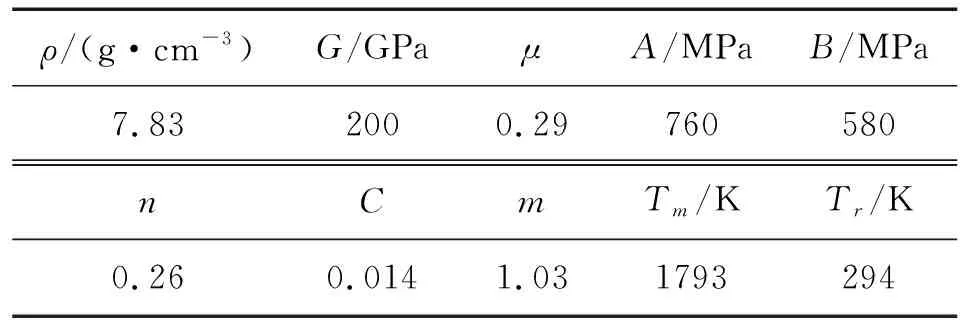
表2 靶體材料參數

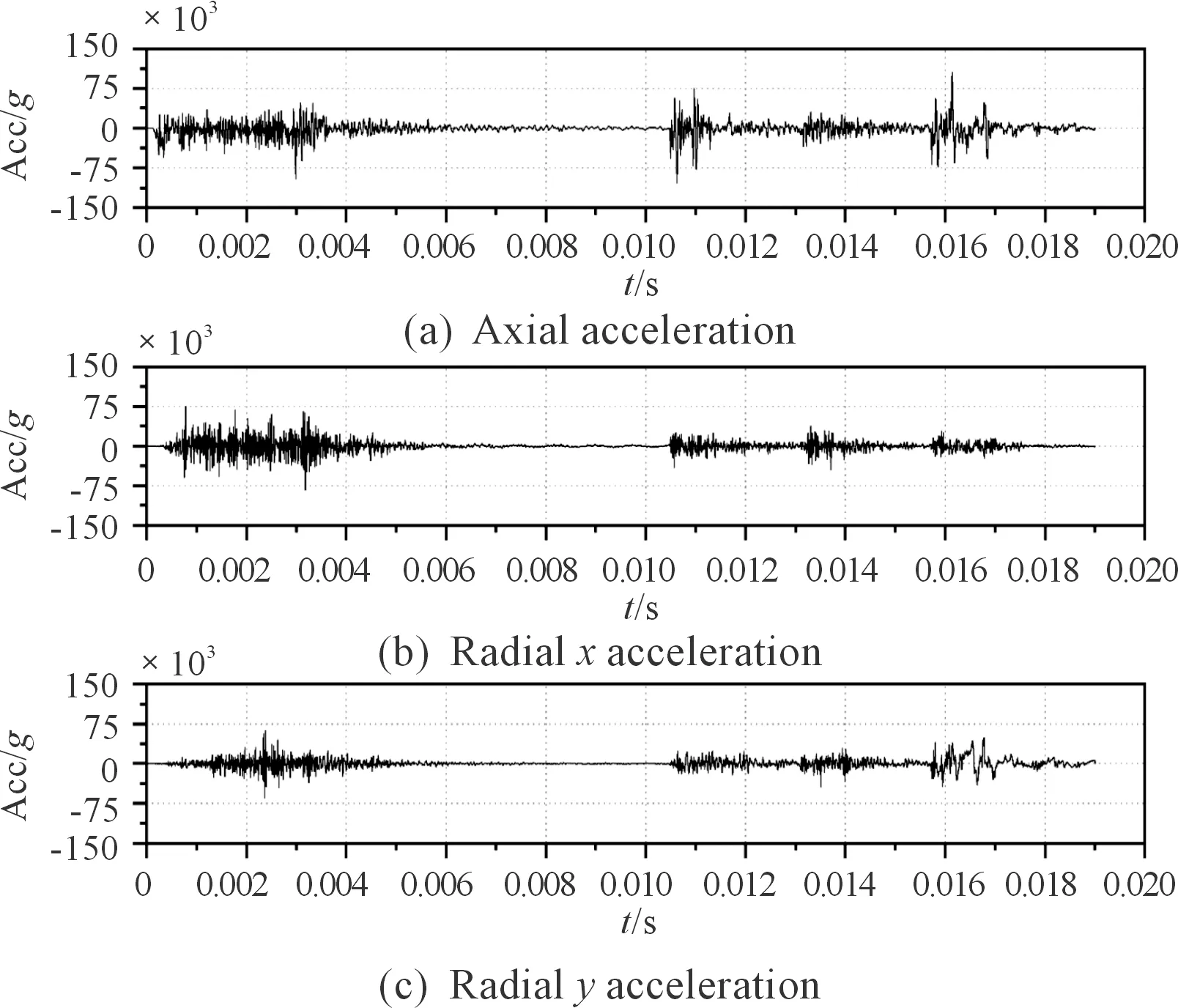
圖2 仿真過載得到的軸向加速度及徑向加速度曲線

圖3 空間坐標系與運動坐標系變換示意圖

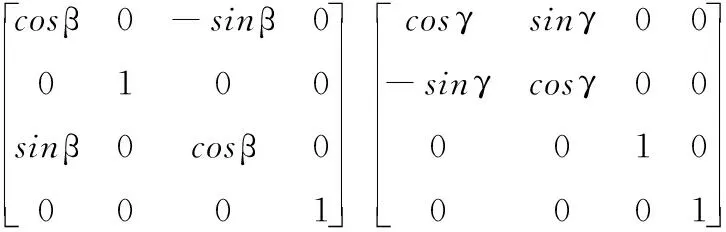
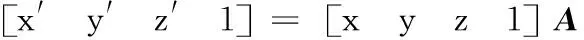
式中：矩陣A為空間固定坐標系到彈體運動坐標系的變換矩陣。將仿真數據代入坐標系變換公式得到新的實測過載，如圖4所示。

圖5為仿真所得姿態(tài)角與實測計算所得姿態(tài)角的對比，兩者變化趨勢基本相同，但計算結果在某些時刻不能很好描述姿態(tài)角的細微變化，這是由于二次積分所產生的誤差所導致，最大誤差在5°左右。結果表明通過三軸加速度傳感器實測過載計算彈體偏轉角在理論上是可行的，仿真結果對比驗證了計算模型的有效性。

圖4 計算過載得到的軸向速度及徑向速度曲線

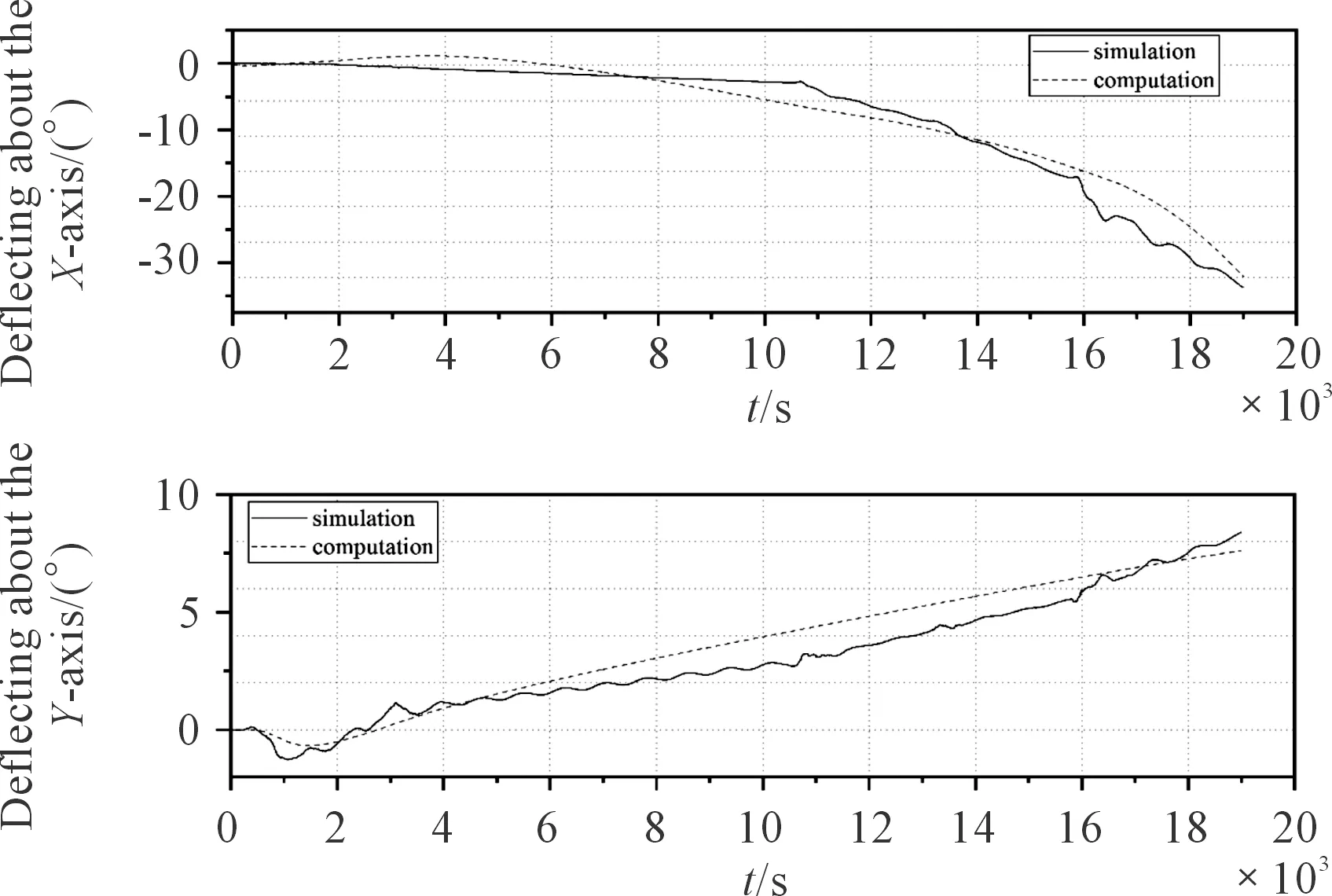
圖5 仿真與實測姿態(tài)角曲線

4 結論

針對彈體連續(xù)侵徹多層靶板，在彈體初始著速、著角已知的情況下，從坐標系變化出發(fā)，在彈體姿態(tài)角變化較大的情況下，通過三軸加速度傳感器推導出了彈體姿態(tài)角的計算模型；采用LS-DYNA有限元分析軟件進行了仿真分析，并將仿真獲得的三軸加速度信號進行坐標系變換，通過MATLAB程序計算，對該算法進行了驗證。作者提供了一種基于三維加速度傳感器的彈體姿態(tài)角變化實時計算方法，對侵徹引信識別具有參考價值。