“三線八角”——平面幾何的敲門磚

呂宗儒

中華文化，源遠流長，從不少的古詩詞中，我發現了數學的蛛絲馬跡。“君住長江頭，我住長江尾，日日思君不見君”，這就像兩道凄美的平行線，永無相交。但是它們“共飲長江水”，此時，江水好似兩線間的樞紐，溝通了兩線，形成許多關聯。它們形成了幾個特殊的夾角，分別為：同位角，內錯角，同旁內角。

你或許已經猜到了，這便是鼎鼎有名的“三線八角”模型。這個模型是初中幾何一個很重要的知識點，在判定兩直線平行以及探究角之間的數量關系上有著舉足輕重的作用。今天，我帶大家認識“三線八角”模型。

兩條直線被第三條直線所截，共頂點處的角分別為對頂角和鄰補角;不共頂點處有同位角、內錯角，還有同旁內角。分清同位角、內錯角和同旁內角的關鍵是找準截線和被截線。

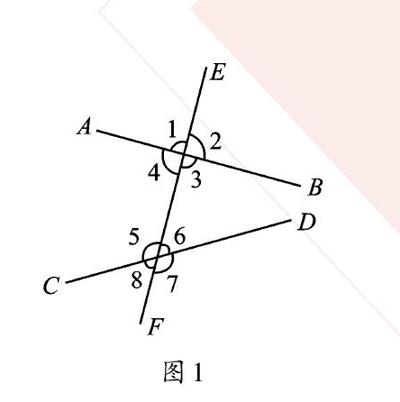
如圖1，直線AB、CD分別與直線EF相交，形成了8個角。

同位角：∠1的兩邊所在的直線是AB和EF，∠5的兩邊所在的直線是CD和EF，它們的公共邊是EF，所以EF是截線，AB、CD是被截線，∠1與∠5分別在截線的同旁，被截線的同側，故∠1與∠5是同位角。具備這一位置關系的角還有∠2與∠6、∠3與∠7、∠4與∠8。

內錯角：根據定義可知，這兩個角應該在“內”部，并且交錯。因為截線只有一條，無所謂內外，所以這兩個角一定是在被截線的內部，且在截線的兩側交錯。不共頂點處的8個角中，具有上述位置關系的角是∠3與∠5、∠4與∠6。

同旁內角：根據定義可知，這兩個角也應在“內”部，并且在同旁。因為截線只有一條，無所謂內外，所以這兩個角一定是在被截線的內部，且在截線的同旁。……