垂直發射彈藥脈沖發動機轉彎控制方法*

鄧海鵬,栗金平,姜 智,梁益銘,楊姝君

(西安現代控制技術研究所, 西安 710065)

0 引言

垂直發射方式由于其方位無死角、響應快等優點,在地空、地地導彈以及智能彈藥等領域被廣泛應用。垂直發射彈藥的彈道可以分為垂直上升段、快速轉彎段和導引段。為了在動壓較低的上升段實現快速轉彎,往往需要借助燃氣舵、脈沖發動機等產生轉彎力矩,使彈軸轉向發射前裝訂的空間方位。

1 問題提出

文中以某智能彈藥為背景,對其轉彎段控制方法進行研究。該彈在垂直發射后接近零速時通過4個尾部脈沖發動機進行彈體姿態調整,將彈體姿態調整到指定空間方位,隨后推進旋轉發動機點火,將彈藥推向目標。調姿結束后彈藥不再控制,如果兩個方向姿態不能同時到達指定值,則炮口擾動就會產生姿態控制誤差(炮口擾動本身也會使兩個方向姿態不能同時到達指定值)。為了將彈藥準確推向目標,需要設計一種考慮炮口擾動的姿態調整控制方案來實現彈藥姿態的準確調姿。

2 技術方案

文中所研究智能彈藥的工作過程可以簡單描述為:地面測量裝置在彈體發射前通過測量得到目標相對于發射系的空間方位并在激發前裝訂信息給彈藥;彈載慣性裝置實時測量彈體姿態角及姿態角速率;彈載計算機利用裝訂信息及慣性裝置測量信息經過坐標轉換、限幅、計算偏差角度、進行點火策略邏輯運算等,給出4個脈沖發動機點火指令,產生直接力控制彈體轉向空間指定方位(見圖1)。

圖1 工作過程示意圖

由于彈藥采用垂直發射,文中采用如圖2所示歐拉角轉動次序。

圖2 坐標轉動順序

從彈體尾部朝著頭部看,發動機安裝如圖3所示:4個姿控脈沖發動機編號1、2、3、4,當彈體系的oxz平面與水平面平行時,慣導的水平姿態角(俯仰角、滾轉角)輸出為0。并假設每個脈沖發動機點火會產生165°/s的彈體姿態角速率。

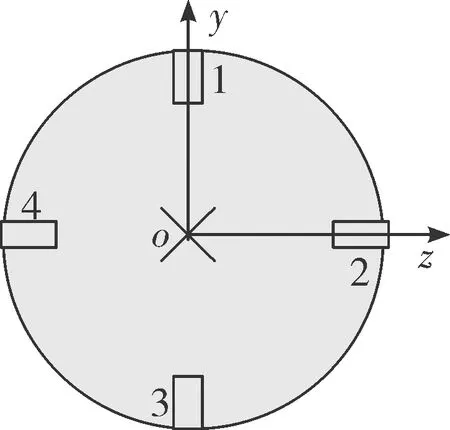
圖3 脈沖發動機布局(從彈體尾部看)

根據彈載慣性裝置提供的彈體的姿態角及姿態角速率定義新彈體系,使得俯仰、偏航姿態角速率在新彈體系下投影大小相等。因此新彈體系是將彈體系繞其縱軸旋轉一定角度Δγ,旋轉角度按式(1)、式(2)計算:

(1)

(2)

式中:ωz、ωy為彈體的俯仰、偏航角速率;Fsp、Fsy為俯仰、偏航點火標志(0為未點火,1為已點火);C1、C2為控制偏差角;?c、ψc為發射系下目標空間方位;?、ψ、γ為彈體相對發射系的實時空間姿態。結合新彈體系定義及上面計算得到的Δγ,彈載計算機通過坐標轉換將發射系下目標空間方位轉換到實時新彈體坐標系,方法如下:

(3)

式中:A1、A2、A3分別為目標空間方位的單位向量在新彈體坐標系XbYbZb三個軸上的分量。

下面計算控制偏差:

(4)

進行限幅:

(5)

控制偏差計算:

(6)

式中:C1、C2、C3為目標空間方位在新彈體系下投影的偏差角度;HD為常數57.3;DHP為兩個方向角偏差作差取絕對值。

脈沖調姿發動機點火策略:

1)開始轉彎點火策略

若C3(200)≤0.95°,則:

Fs1=0,Fs2=0,Fs3=0,Fs4=0

(7)

若C3(200)>0.95°,|C1(200)|≥|C2(200)|,C1(200)≥0,則:

Fs1=1,Fs3=0,Fsp=1

(8)

若C3(200)>0.95°,|C1(200)|≥|C2(200)|,C1(200)<0,則:

Fs1=0,Fs3=1,Fsp=1

(9)

若C3(200)>0.95°,|C1(200)|<|C2(200)|,C2(200)≥0,則:

Fs2=1,Fs4=0,Fsy=1

(10)

若C3(200)>0.95°,|C1(200)|<|C2(200)|,C2(200)<0,則:

Fs2=0,Fs4=1,Fsy=1

(11)

2)另一方向點火策略

若k≥200,Fsp=1,Fsy=0,DHP≤Δμ,C2(k)≥0,則:

Fs2=1,Fs4=0,Fsy=1

(12)

若k≥200,Fsp=1,Fsy=0,DHP≤Δμ,C2(k)<0,則:

Fs2=0,Fs4=1,Fsy=1

(13)

若k≥200,Fsp=0,Fsy=1,DHP≤Δμ,C1(k)≥0,則:

Fs1=1,Fs3=0,Fsp=1;

(14)

若k≥200,Fsp=0,Fsy=1,DHP≤Δμ,C1(k)<0,則:

Fs1=0,Fs3=1,Fsp=1

(15)

3)俯仰通道轉彎結束判定

若k≥200,Fsp=1,|C1(k)|≤0.95°,Fs1+Fs3=1,則:Fs1=1,Fs3=1

(16)

4)偏航通道轉彎結束判定

若k≥200,Fsy=1,|C2(k)|≤0.95°,Fs2+Fs4=1,則:Fs2=1,Fs4=1

(17)

若t>30,則:

(18)

式中:Fsi(i=1,2,3,4)為i號發動機點火標志,俯仰、偏航方向點火標志初值都為0,Δμ=0.001。

3 仿真分析

假設彈載慣性裝置敏感彈體相對發射系初始姿態為?=90°、ψ=0°、γ=0°,彈體出筒時的速度為11.7 m/s,出筒擾動為[ωx0,ωy0,ωz0]=[0,0,-57.3°/s],地面測量裝置測量目標相對發射系空間方位為?c=10°、ψc=10° ,調姿脈沖發動機收到點火指令后產生一個瞬時力,忽略發動機點火延遲。

利用Matlab中Simulink模塊搭建彈體六自由度方程并進行仿真。

繪制姿態控制脈沖發動機工作時序如圖4、圖5所示,從圖中可以看出發動機點火順序為3、4、1、2號發動機,首先是3號發動機點火產生俯仰方向低頭力矩,然后是4號發動機點火產生偏航正向力矩,最后是1、2號發動機點火產生止動力矩。比較圖4和圖5發現,沒定義新彈體系的仿真結果是1、2號止動發動機點火時間間隔47 ms,而定義新彈體系的仿真結果是1、2號止動發動機幾乎同時點火。

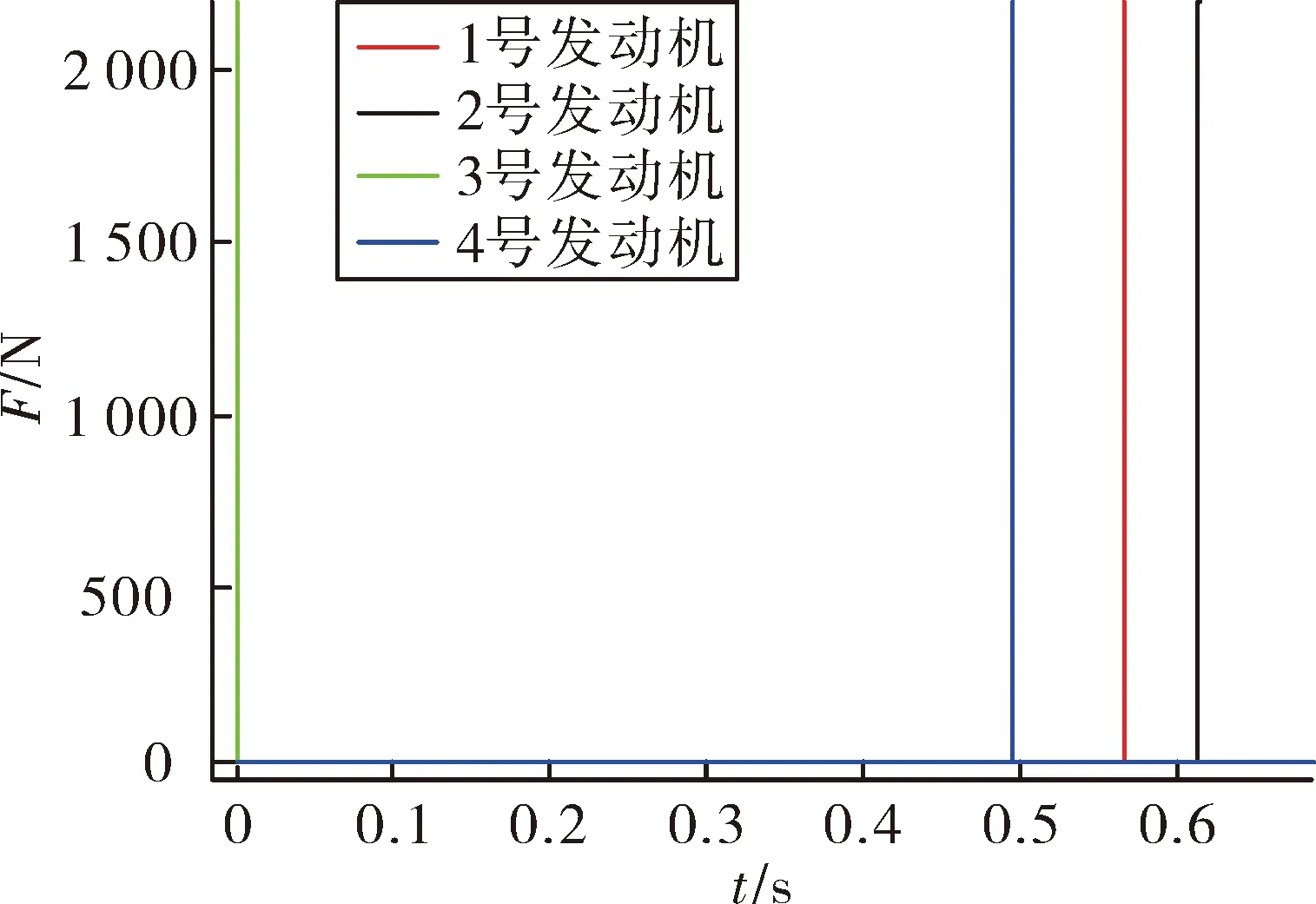
圖4 不定義新彈體系的調姿脈沖發動機工作時序

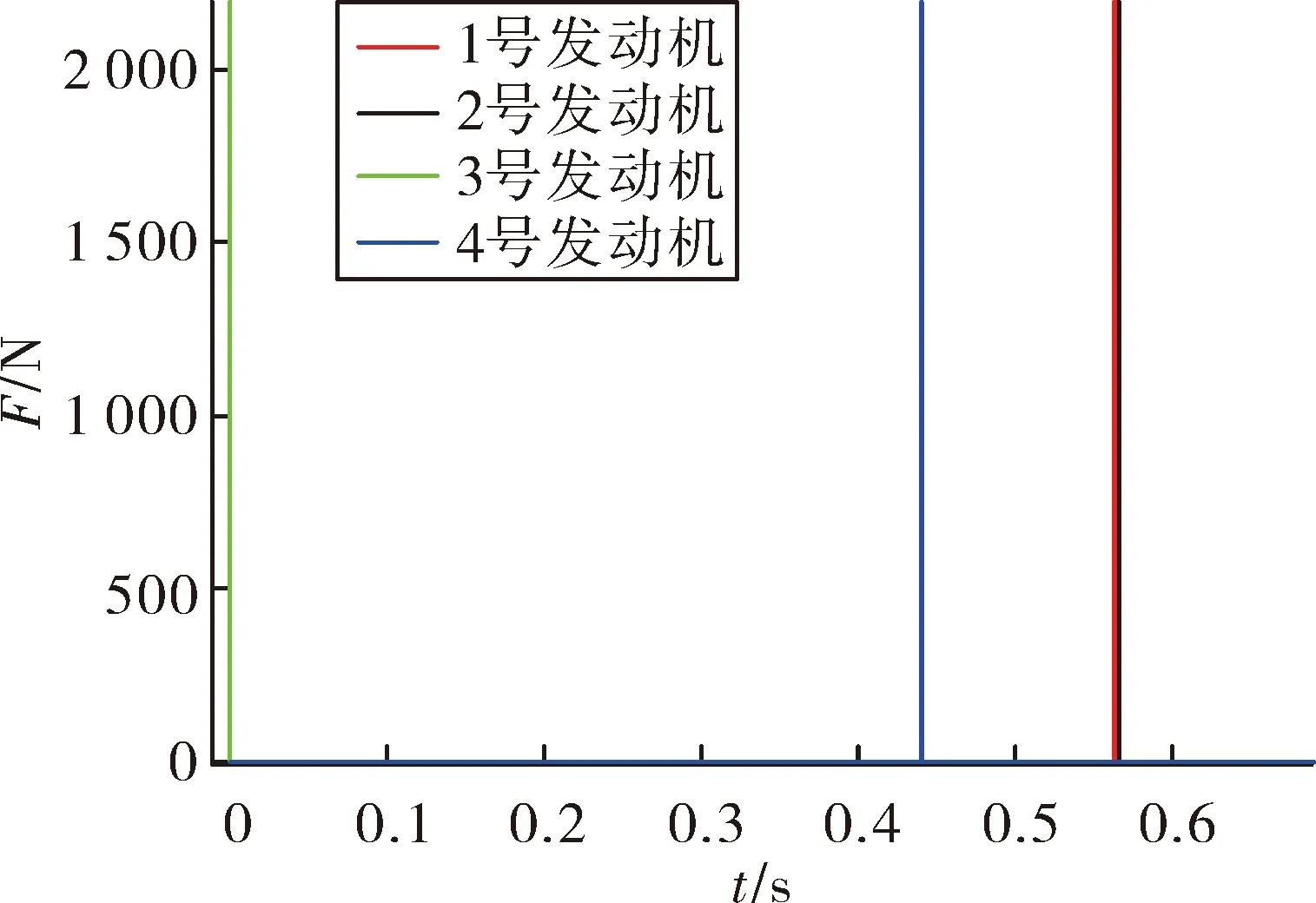
圖5 定義新彈體系的調姿脈沖發動機工作時序

繪制彈體姿態角速度曲線如圖6、圖7所示,從圖中可以看出彈體姿態角速度變化符合發動機點火時序。調姿發動機工作結束后,炮口擾動姿態角速率依舊存在,并不能被消除,所以需要考慮炮口擾動,盡量使俯仰和偏航角同時到達空間指定值。

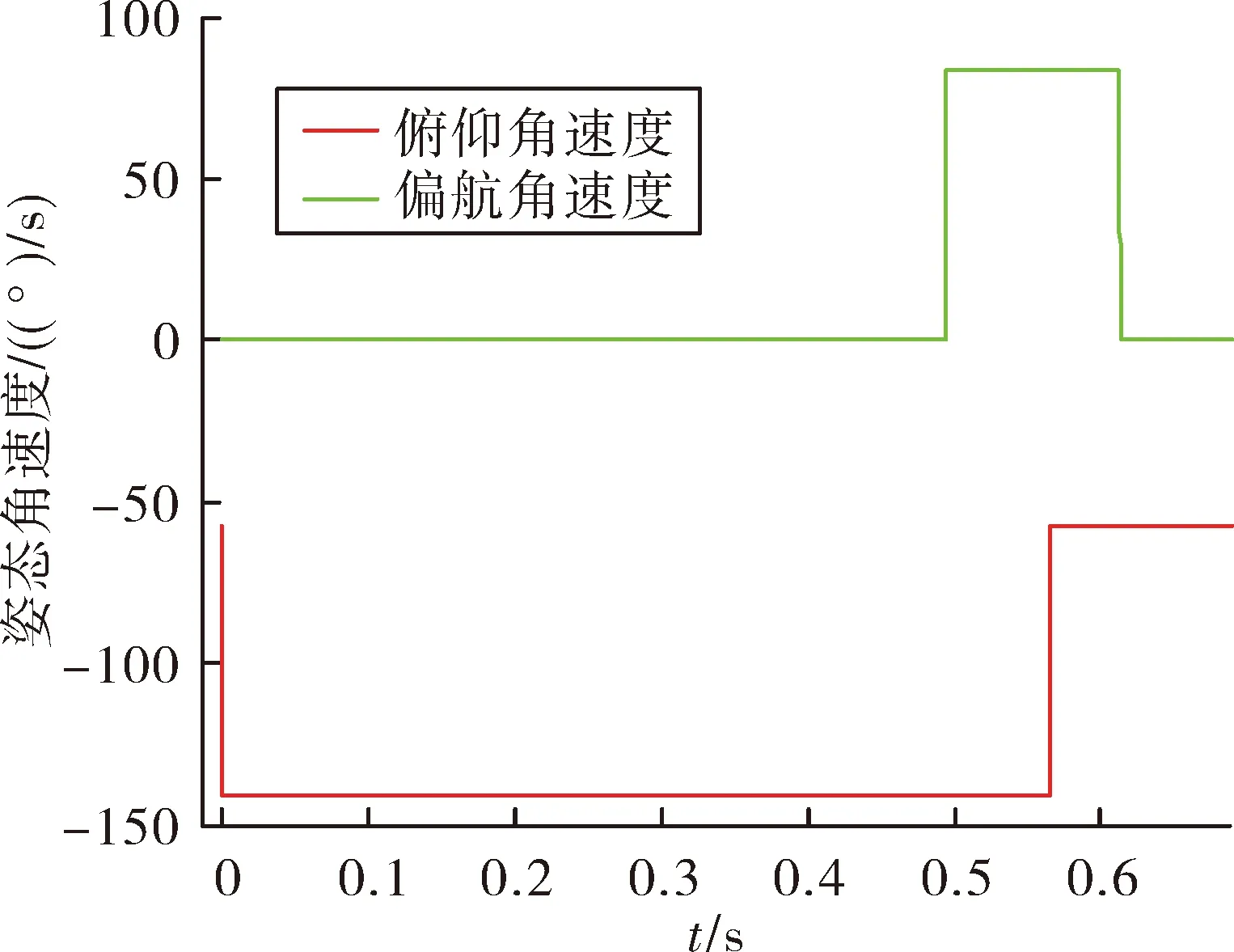
圖6 不定義新彈體系的彈體姿態角速度曲線

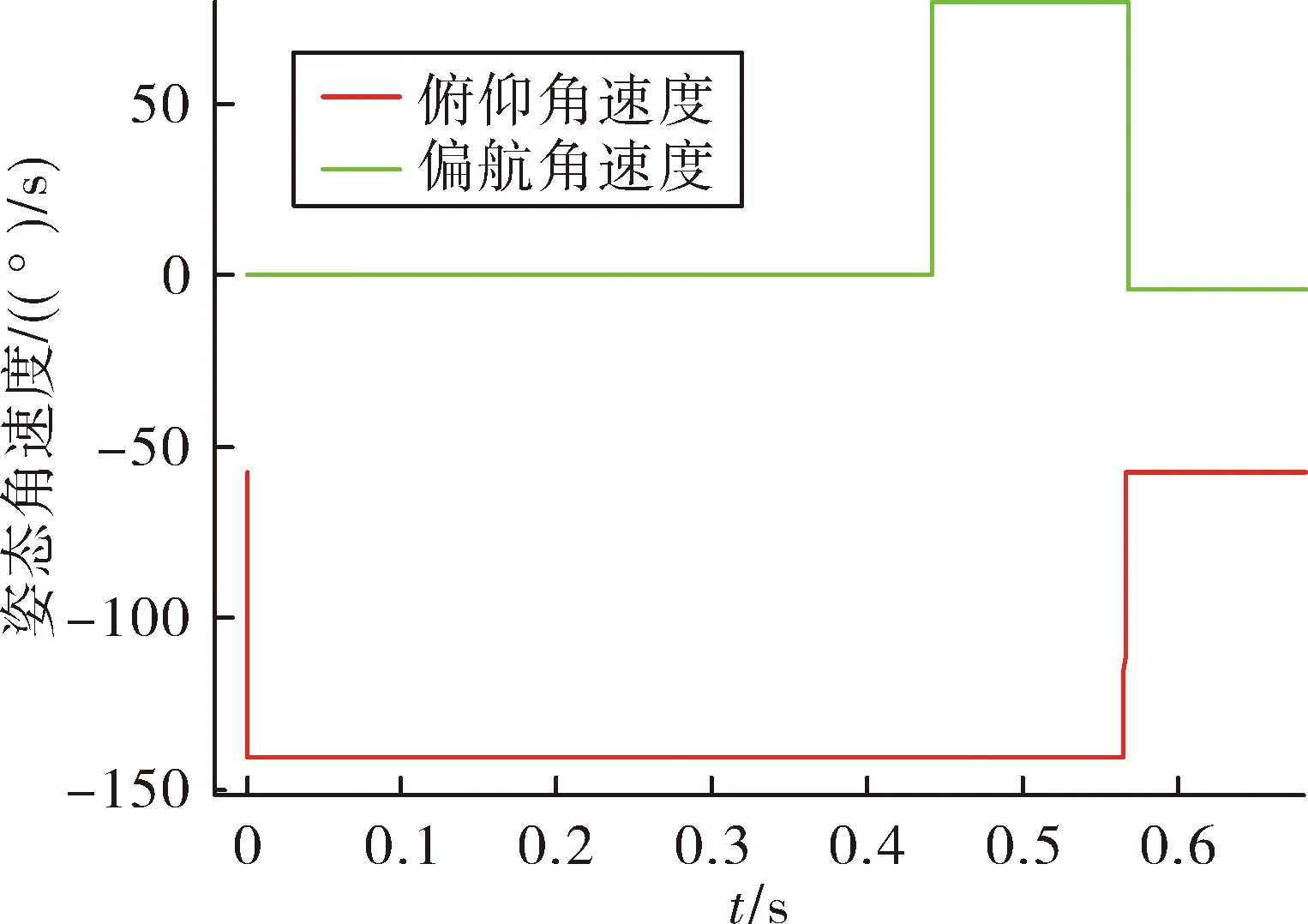
圖7 定義新彈體系的彈體姿態角速度曲線

繪制彈體姿態角如圖8、圖9所示,從圖中可以看出彈體初始俯仰、偏航姿態角分別為90°、0°,隨后在控制作用下俯仰角減小,當控制角減小到一定值后偏航角在控制作用下開始增加。不定義新彈體系方案,俯仰先到達指定值,47 ms后偏航角到達指定值,而此時由于炮口擾動俯仰角變化為7.5°,比指定值小了2.5°,此時如果旋轉推進發動機點火,將會在俯仰方向產生較大的誤差;定義新彈體系的方案,當t=565 ms時,俯仰和偏航角幾乎同時到達慣性空間指定的方位,因此可以實現存在較大炮口擾動時的彈體姿態準確控制。

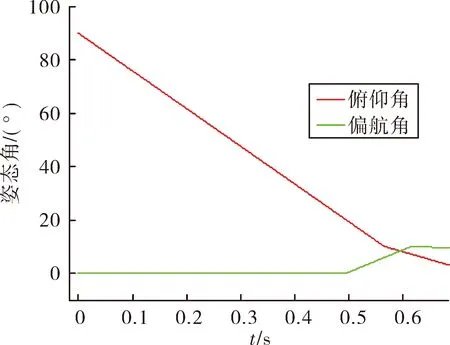
圖8 不定義新彈體系的彈體姿態角曲線

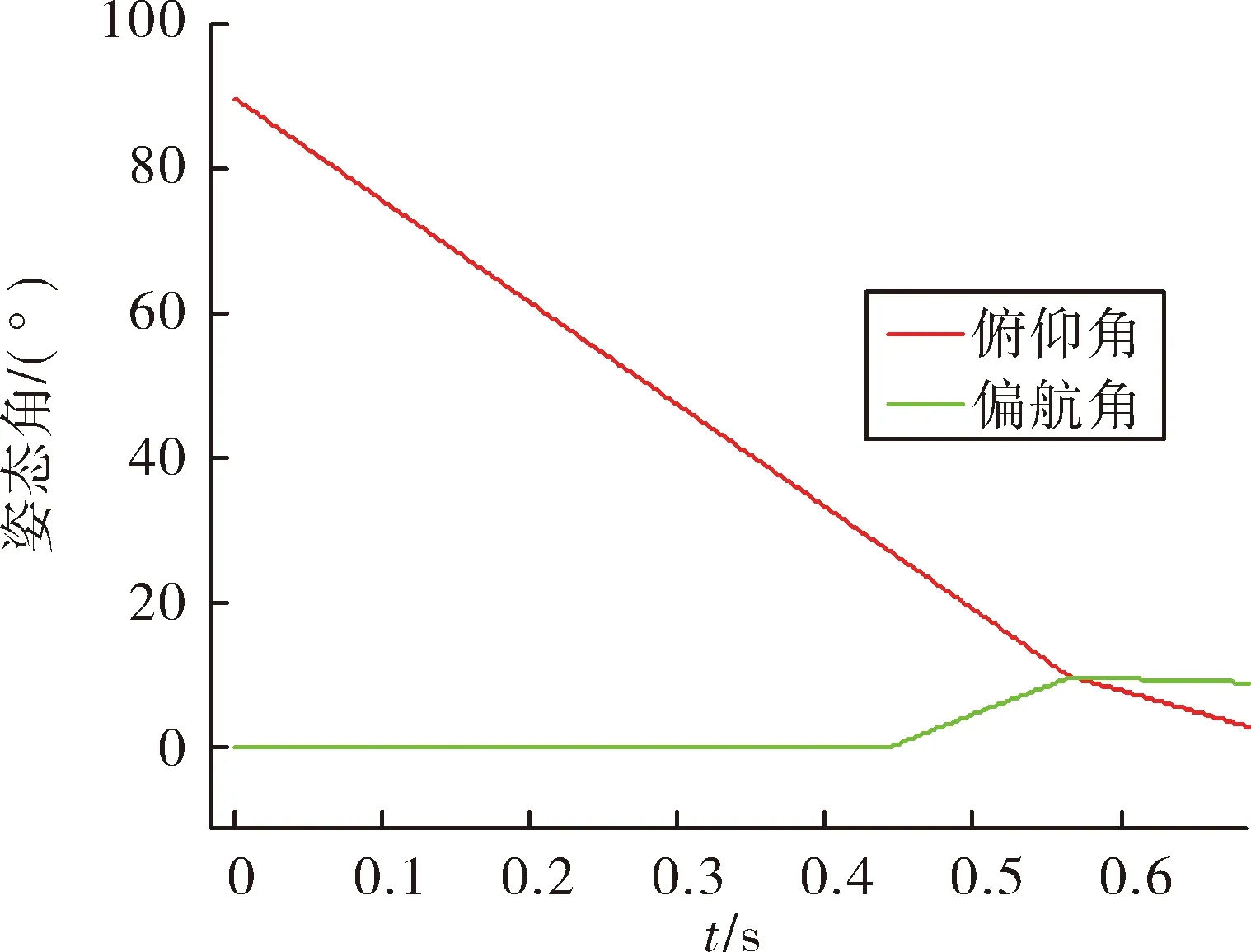
圖9 定義新彈體系的彈體姿態角曲線

仿真結果驗證了文中研究調姿控制方法的有效性。

4 結論

文中針對某垂直發射彈藥采用脈沖調姿發動機進行轉彎的控制方法進行了研究,尤其當初始擾動較大時,為避免擾動對姿態控制精度的影響，定義了新的彈體坐標系,通過將空間方位投影到新彈體坐標系,計算控制誤差,并通過邏輯運算得到4個脈沖發動機點火指令。通過仿真驗證,比未定義新坐標系的方法在抗初始擾動方面有顯著優勢。