基于模糊神經網絡的高精度電機自抗擾控制*

何 靜,肖 建,倪 亮,于巍巍,楊成山,鄭廣瑜

(上海無線電設備研究所, 上海 201100)

0 引言

太赫茲雷達采用二維交流伺服電機控制發射面天線運動,以實現雷達的波束精確指向控制。需要電機具備控制精度高、過載能力強、響應速度快以及魯棒性高等優點。采用傳統的PID控制算法穩定性較差,容易產生超調,抗干擾性能較低,從而影響雷達的測量精度。

自抗擾技術(ADRC)[1]是采用誤差反饋方法,通過采用ESO對電機中未知及難以處理的擾動加以觀測和補償,從而提高系統精度和抗干擾性[2]。然而在實際系統實現過程中,ADRC算法涉及的可調參數太多,需要通過不斷實踐選取合適的參數才能使系統達到一個好的效果。文獻[3-5]提出結合模糊控制的優勢來解決ADRC參數難以確定等不足。但模糊控制中的模糊推理是根據一定的經驗來進行推斷,其不免局限性且不能使控制系統達到最優。

為了提高交流伺服電機的適應能力和抗干擾性能,文中提出一種基于模糊神經網絡的高精度交流伺服電機的自抗擾控制方法,通過運用模糊神經網絡的自學習優點,解決模糊控制中需要通過一定的摸索經驗來調節參數的問題,并且結合自抗擾控制優點,有效提高交流伺服電機的控制精度及抗干擾性。

1 交流伺服電機的數學模型

交流伺服電機等效框圖如圖1所示。

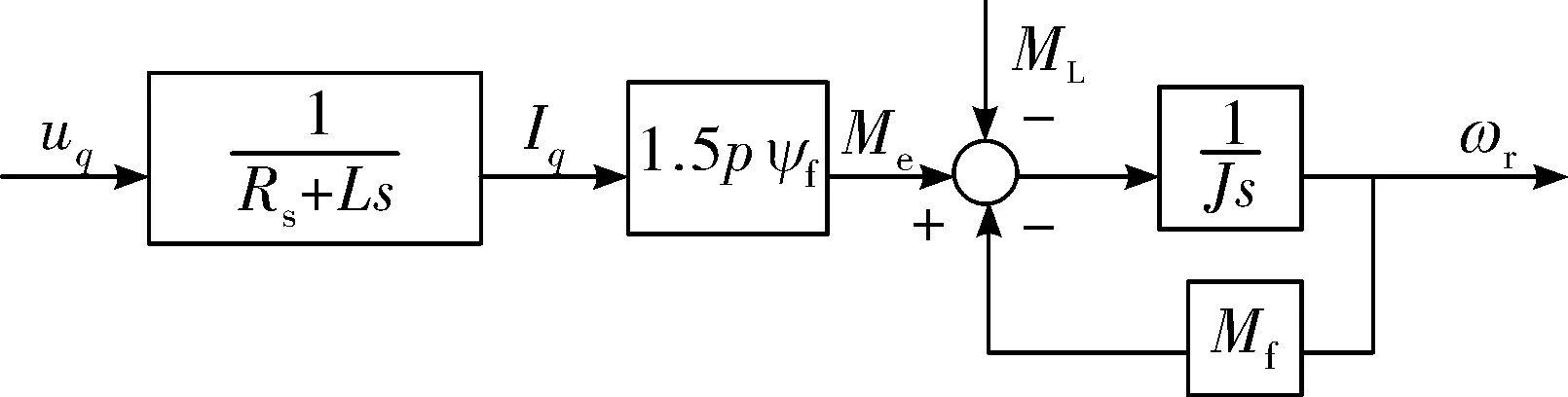
圖1 交流伺服電機等效框圖

2 控制系統設計

2.1 系統總體框圖

采用基于模糊神經網絡的高精度電機的自抗擾控制的系統控制部分主要由自抗擾控制和模糊神經網絡控制兩部分組成。自抗擾控制用于觀測位置擾動,并根據輸入位置誤差進行反饋和補償;模糊神經網絡用于調節自抗擾控制中關鍵參數,從而使系統達到自適應調節的目的。系統的其它部分采用Id=0及SVPWM控制策略。整個系統框架如圖2所示。

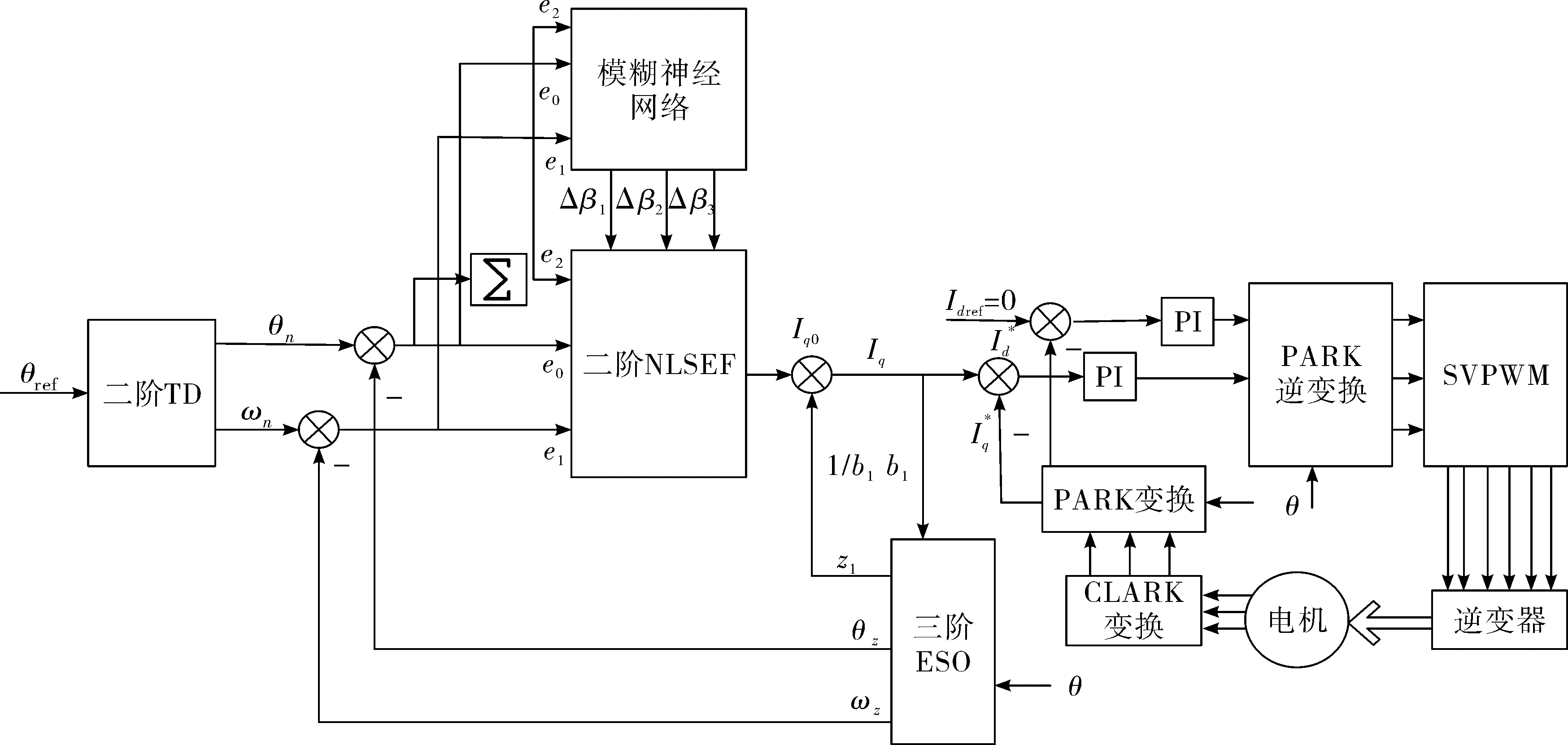
圖2 系統控制總體框圖

2.2 自抗擾控制

自抗擾控制部分主要分為3個部分[6]：跟蹤-微分器(TD);擴張狀態觀察器(ESO);非線性狀態誤差反饋(NLSEF)。跟蹤-微分器(TD)為根據參考位置信息分解出供NLSEF參考的過渡位置和速度;擴張狀態觀察器(ESO)用于根據電機反饋的位置信息及內部狀態信息估計出系統的反饋位置和速度;非線性狀態誤差反饋(NLSEF)通過比較TD和ESO的輸出誤差,再根據當前系統狀態計算出實際反饋量。整個自抗擾控制部分連接如圖3所示。

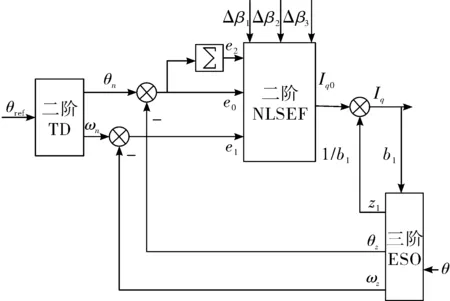
圖3 自抗擾控制連接圖

二階跟蹤微分器TD設計如下[7]：

fh=rfal(θn-θref,α,h0)

(1)

θn(k+1)=θn(k)+g·ωn(k)

(2)

ωn(k+1)=ωn(k)-g·fh

(3)

式中:fal如公式(4)所示;r為速度因子；α為非線性因子;h0為TD的濾波因子;θref為參考的輸入角度；θn為根據θref安排的過渡過程；ωn為θn的微分形式;g為積分步長。

(4)

式中：ε為角度誤差；α為非線性因子,0<α<1；σ為濾波因子；δ>0；sign為符號函數。

三階擴張狀態觀測器(ESO)設計如下:

e(k)=θz(k)-θ(k)

(5)

fe=fal(e(k),0.5,δ)

(6)

fex=fal(e(k),0.25,δ)

(7)

θz(k+1)=θz(k)+h(ωz(k)-β01e(k))

(8)

ωz(k+1)=ωz(k)+h(z1(k)-β02fe+b1Iq(k))

(9)

z1(k+1)=z1(k)+h(-β03fex)

(10)

式中:θz(k)和ωz(k)為第k個運算周期的電角度和角速度估計值;θ(k)為實際電角度反饋值;z1(k)為擾動的觀測值;fal為公式(4)所示;β01、β02、β03為各階狀態觀測器系數;h為位置環控制周期;Iq(k)為第k個周期的電流輸出值;b1為Iq(k)反饋系數;δ為濾波因子。

非線性狀態誤差反饋(NLSEF)設計如下:

e0(k)=θn(k)-θz(k)

(11)

e1(k)=ωn(k)-ωz(k)

(12)

(13)

Iq0(k)=β0fal(e0,α0,δ)+β1fal(e1,α1,δ)+
β2fal(e2,α2,δ)

(14)

Iq(k)=Iq0(k)-z1(k)/b1

(15)

式中:θn(k)和ωn(k)為TD中第k個運算周期的電角度和電角速度過渡參考值;θz(k)和ωz(k)為ESO中第k個運算周期的電角度和角速度估計值;β0、β1、β2分別為誤差函數fal的不同增益,fal如公式(4)所示;α0、α1、α2為非線性因子;z1(k)為擾動的觀測值。

2.3 模糊神經網絡

由于自抗擾控制部分的主要控制參數β0、β1、β2對系統的影響較大,因此采用模糊神經網絡根據輸入誤差信號e0、e1、e2的大小,通過誤差反向傳播來調節模糊神經網絡權值,從而達到對控制參數β0、β1、β2自適應調節的目的。

2.3.1 模糊神經網絡分層

模糊神經網絡分為5層,整個框圖如圖4所示。

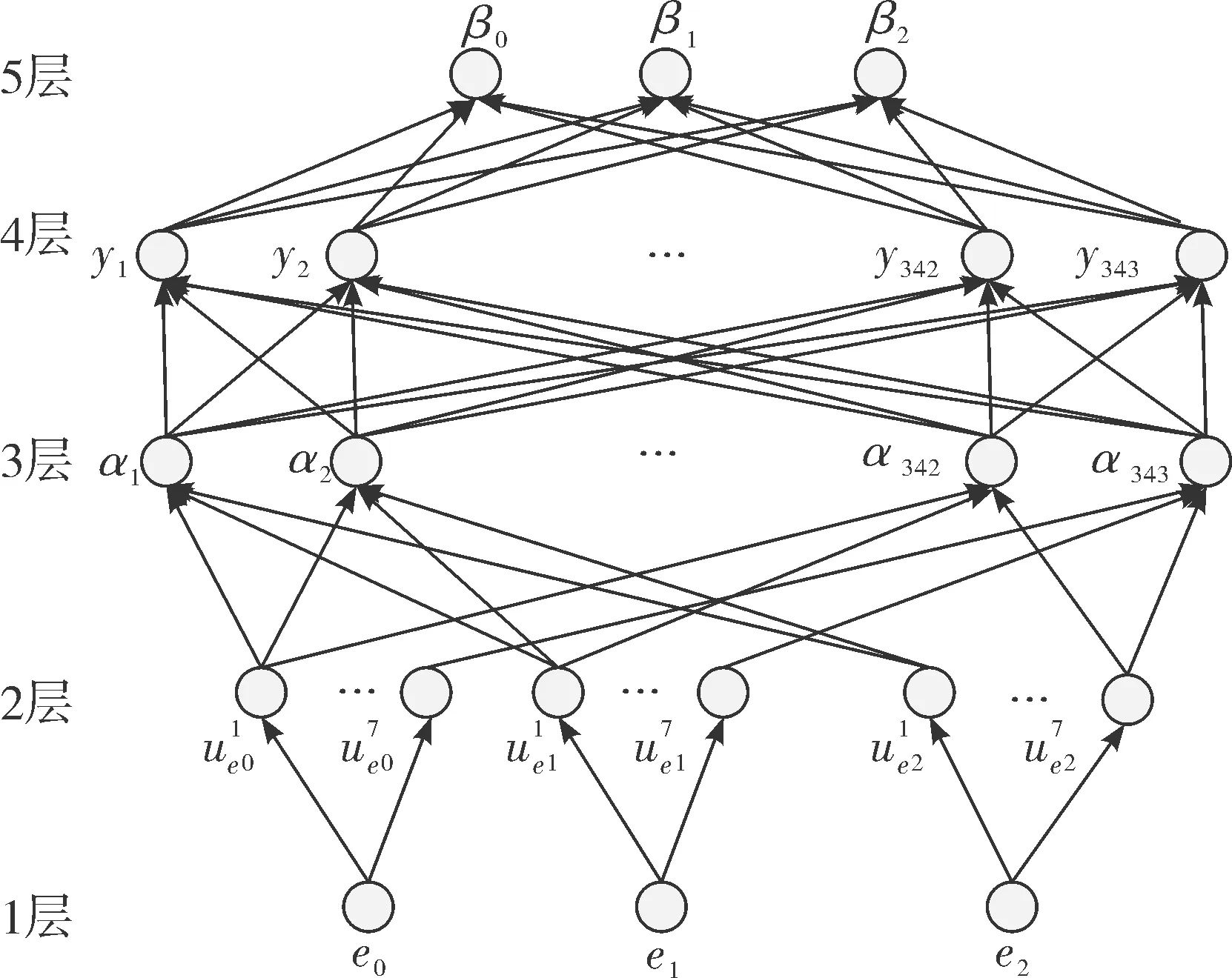
圖4 模糊神經網絡結構圖

第一層為輸入層,為自抗擾控制中NLSEF的輸入:e0、e1、e2是精確值,節點數N1=3。

第二層為輸入變量的隸屬函數層,為輸入e0、e1、e2的隸屬函數ue0、ue1、ue2,實現輸入變量的模糊化,節點數N2=21,采用式(16)所示三角隸屬函數。

(16)

第三層為“與”層,為隸屬函數ue0、ue1、ue2的模糊規則輸出αi。該層節點個數為模糊規則數。該層每個節點分別與第二層隸屬函數ue0、ue1、ue2相連,共有7×7×7個節點,即343條模糊規則。模糊規則具體如下所示:

ife0is NB ande1is NB ande2is NB thenαi

第四層為“或”層,其為神經網絡的加權輸出yij,節點數為7×7×7×3=1 029。

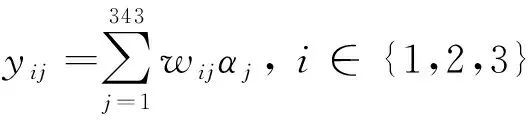
(17)

第五層為清晰化層,輸出為自抗擾控制參數β0、β1、β2,節點數為3。該層與第四層的連接為全連接,它將第四層各個節點的模糊值轉換為精確值。

(18)

2.3.2 誤差反向傳播

模糊神經網絡需要通過誤差反向傳播來調節權值wij,從而使得輸出參數β0、β1、β2達到最優。誤差反向傳播采用最速梯度下降法。輸入數據為自抗擾控制TD中的(θn(k),ωn(k)),輸出為(θz(k),ωz(k)),需要調節的網絡權值為wij。故誤差總和E對wij微分得:

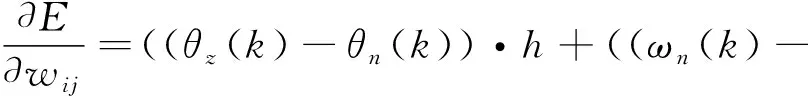
(19)

3 系統仿真及結果分析

3.1 系統仿真

系統采用Matlab中的Simulink進行仿真。其中系統仿真如圖5所示。

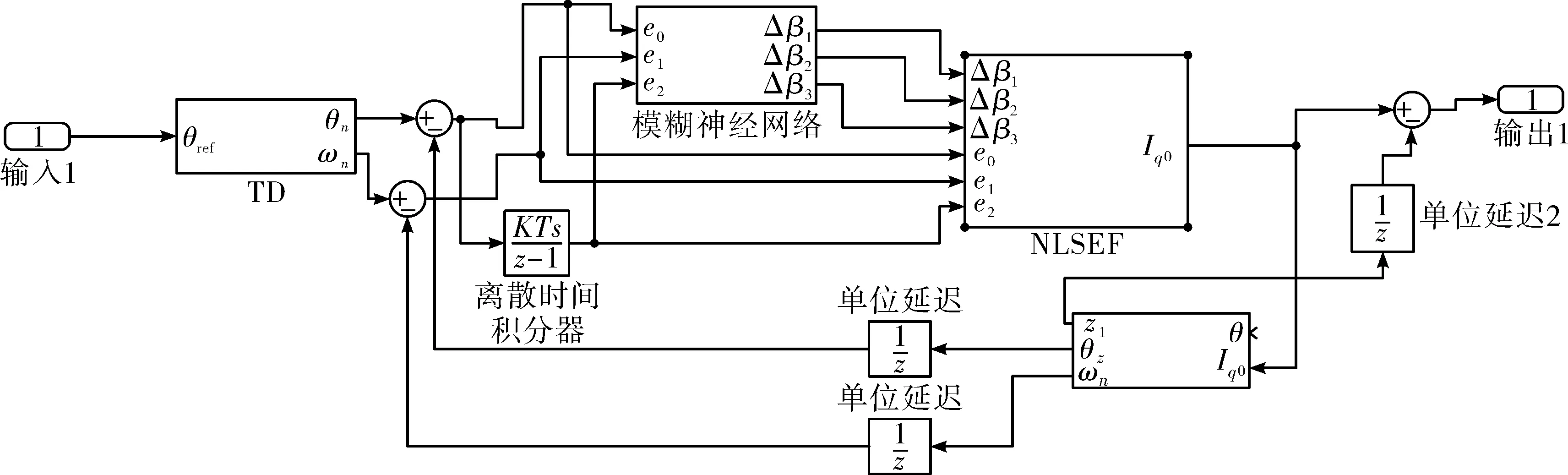
圖5 基于模糊神經網絡的自抗擾控制仿真圖

仿真圖中，TD由式(1)～式(3)組成，其根據經驗設定為：r=0.6,α=0.7,h0=1.6,g=1.6；ESO由式(5)～式(10)組成，根據經驗設定為：β01=1.4，β02=1.7，β03=1.3，δ=0.03；NLSEF由式(11)～式(15)組成，根據經驗設定為：α0=0.2,α1=0.2,α2=0.2;模糊神經網絡由式(16)～式(19)組成，初始值設置為β0=1.6，β1=18,β2=4.7。

給定輸入初始角度為0.75 rad,負載力矩為0 N·m,然后在0.1 s后施加4 N·m的力矩。采用普通PID方法及基于模糊神經網絡的自抗擾控制方法的仿真圖分別如圖6、圖7所示。

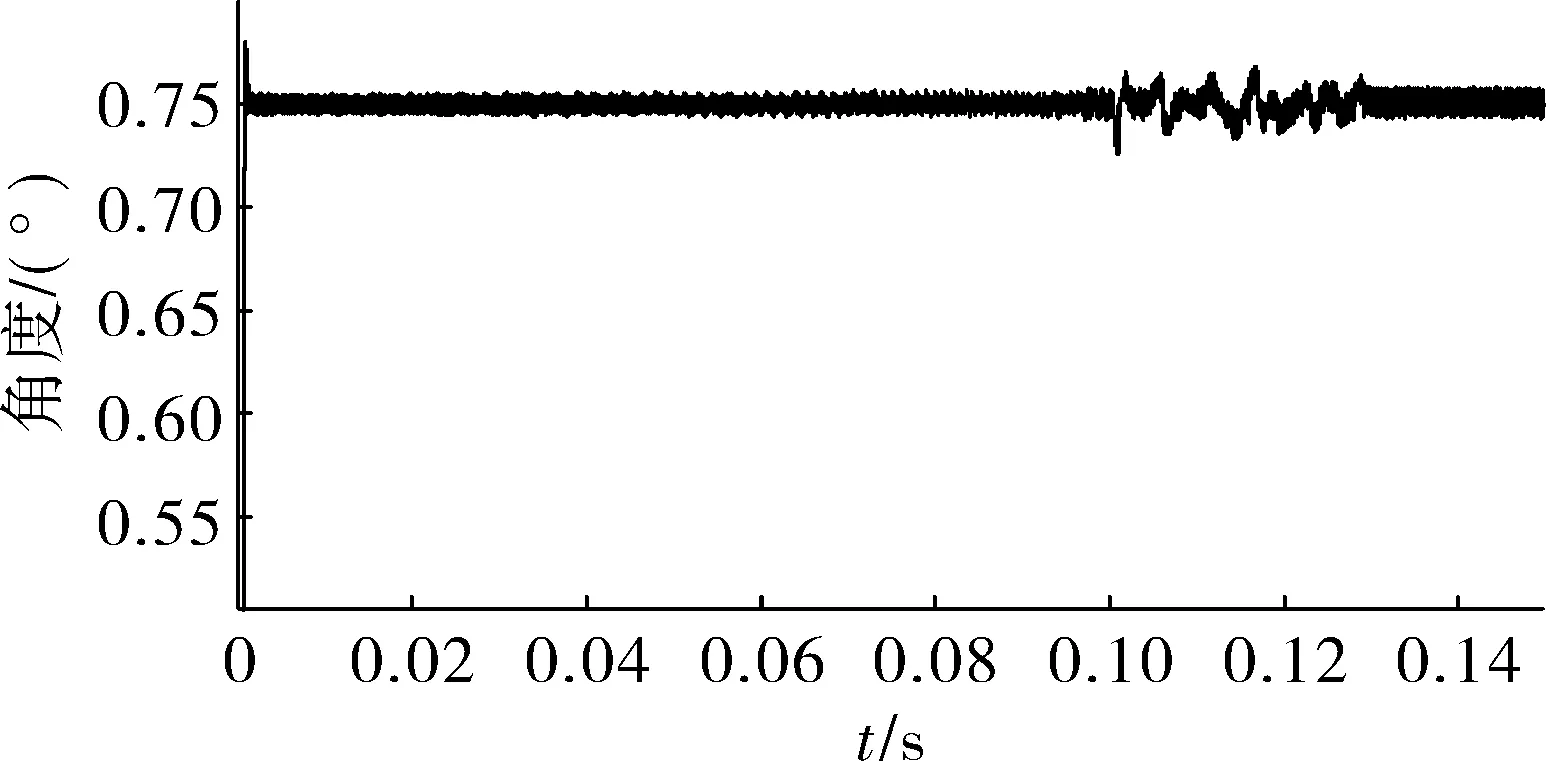
圖6 采用普通PID方法的仿真圖

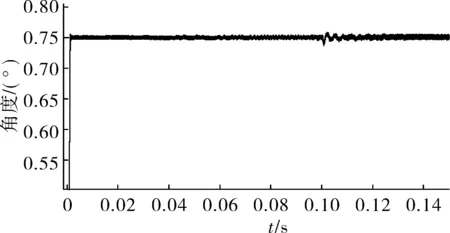
圖7 采用基于模糊神經網絡的自抗擾控制方法的仿真圖

由兩圖對比可以看出,采用基于模糊神經網絡的高精度交流伺服電機的自抗擾控制算法能大幅減少系統的超調量,且提高系統的控制精度和抗干擾性能。

3.2 實驗測試

采用具有強大運算能力的ARM+FPGA架構的zynq7035作為控制芯片,將控制算法移植到芯片中進行實驗。為驗證系統的動態響應能力,使電機在指定角度(174°～198°)內迅速來回擺動,以驗證其快速加速、穩定速度、迅速剎車及克服電機內部不確定因素等動態響應的性能。采用普通PID參數控制與采用基于模糊神經網絡的自抗擾控制的輸入輸出對比及誤差圖如圖8 和圖9所示。從中可以看出,采用普通PID算法時響應曲線具有較大的畸變,且擺動周期會變化,系統誤差較大;采用基于模糊神經網絡的自抗擾控制后,系統相應曲線的畸變很微小,且擺動周期與輸入完全相符,系統誤差很小。

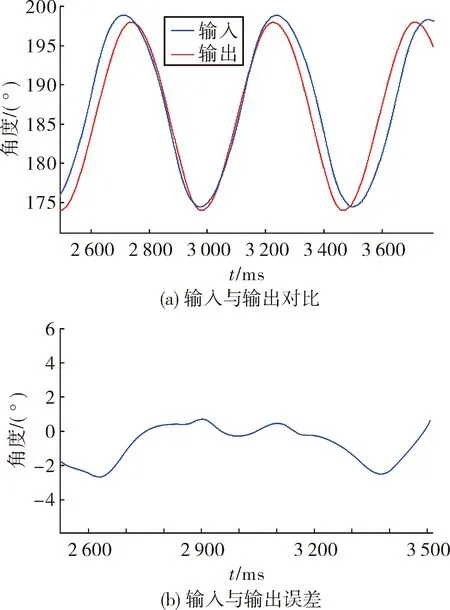
圖8 采用普通PID方法輸入與輸出對比及誤差圖

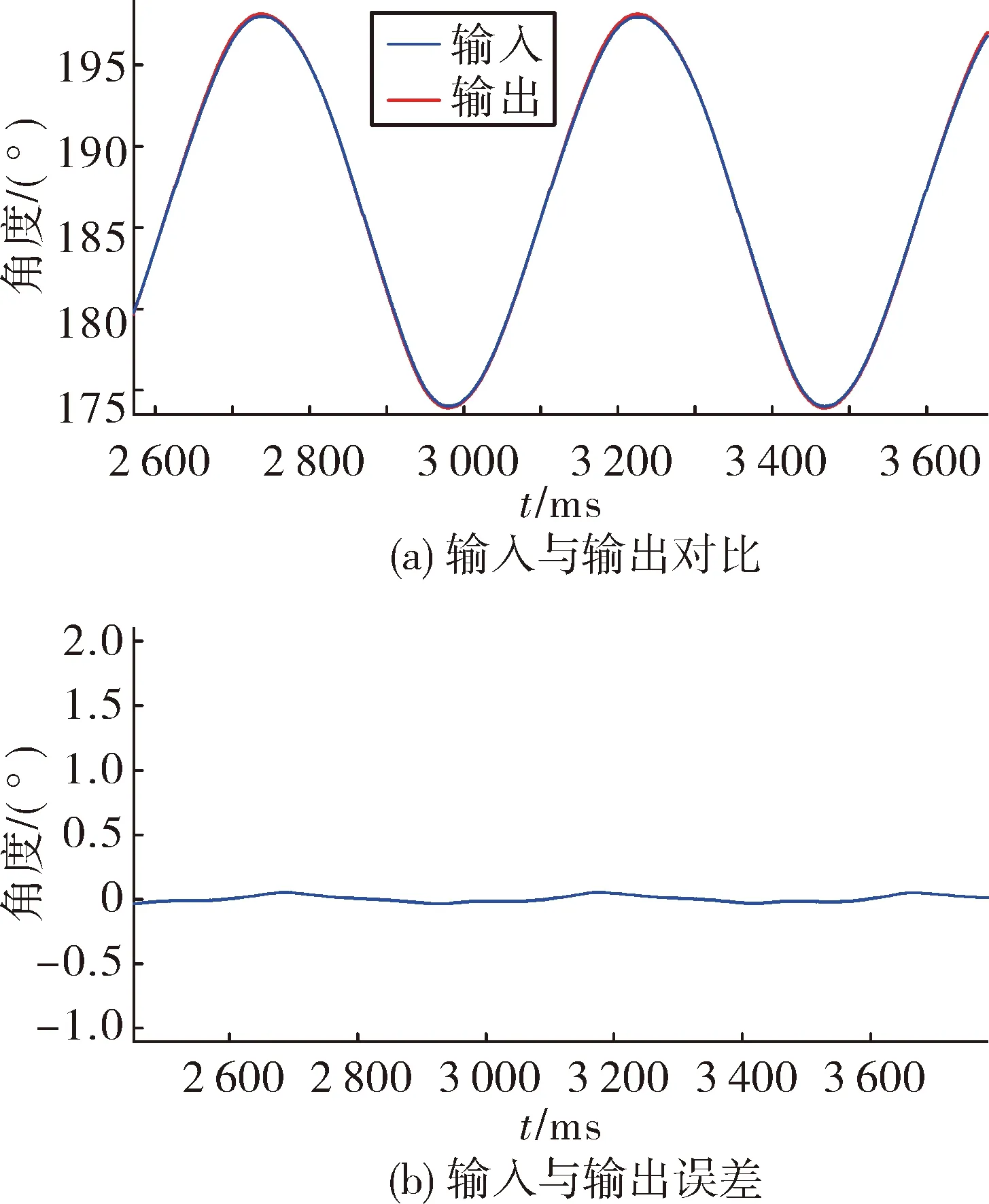
圖9 采用基于模糊神經網絡的自抗擾控制方法輸入與輸出對比及誤差圖

4 結束語

針對傳統PID控制算法控制精度不高,容易產生超調現象,抗干擾性能較差的缺點,設計了一種基于模糊神經網絡的高精度交流伺服電機的自抗擾控制方法,通過模糊神經網絡的自學習功能,解決了模糊控制中需要通過一定的摸索經驗來調試參數的問題,最后通過系統仿真及實驗測試,驗證了該方法在提高交流伺服電機的控制精度及抗干擾性能的實用性。