彈性高超聲速飛行器反步滑模控制器設計*

張 進,馮 昊,凡永華

(1 西北工業大學航天學院, 西安 710072; 2 上海航天控制技術研究所, 上海 201109)

0 引言

高超聲速飛行器能夠以不小于5Ma的速度在大氣層內機動飛行,因而具有極高的軍事應用潛力。高超聲速技術融合航空、航天領域的技術優勢,能夠極大帶動總體、氣動、結構、控制等學科的發展[1-2]。目前,隨著美國HAWC、HSSW等高超聲速飛行器工程項目的提出,表明吸氣式高超聲速技術正朝著武器化、實用化方向發展[3-4]。

高超聲速飛行器因為飛行環境復雜和自身結構特點影響,存在顯著的參數不確定和伺服彈性問題。如果不采取恰當的控制設計方法,輕則影響飛行器控制系統品質,引起飛行器振顫,重則影響飛行器飛行安全,造成飛行器失控、損毀。對于該問題,國內外眾多學者進行了相關研究,并取得了一系列研究成果。文獻[5]研究了低頻彈性模態與剛體耦合對于飛行控制系統設計的影響。在控制系統設計中,將彈性模態影響作為不確定性考慮到剛體的運動控制中去,設計了基于H和μ方法的姿態控制器。文獻[6]考慮了氣動推進/氣動彈性的飛行控制系統其不確定性的來源較為特殊,主要是氣動加熱導致的熱應力和結構彈性模量隨溫度的變化,這樣的變化會引起飛行器的結構動力學特性發生改變。文獻[7]考慮了高速飛行器線性時變動力學系統的不確定性建模問題。其不確定性主要分為兩類:非結構的不確定性模型和實參數的結構不確定性模型。對于模型不確定度的估計表明，根據剛體模型預測的低頻動力學的不確定度明顯大于根據彈性模型所獲得的不確定度,說明對于彈性高速飛行器的控制系統設計而言,剛體飛行器的假設顯然不能夠滿足要求。文獻[8]考慮飛行器縱向靜不穩定性與伺服彈性問題,設計了雙回路魯棒控制器。內環設計變增益控制器，將彈性模型表示成具有仿射參數依賴結構的LPV模型,外環設計魯棒控制器，實現飛行器對攻角指令的精確跟蹤,控制器能夠主動對結構模態進行阻尼,達到抑制伺服彈性的效果。

文中針對彈性高超聲速飛行器在具有參數不確定性情況下的控制問題,結合反步法和彈性自適應滑模控制方法進行控制律的設計。最后通過對某型高超聲速飛行器的數學仿真,驗證了設計控制器的有效性。

1 高超聲速飛行器控制問題描述

1.1 高超聲速飛行器動力學模型

高超聲速飛行器剛體縱向動力學模型為:

(1)

式中：V表示飛行器速度;θ表示飛行器彈道傾角;h表示飛行器高度;ωz為俯仰角速度;α表示攻角;m為飛行器質量;P、X、Y、Mz分別為飛行器的推力、阻力、升力和俯仰力矩。

類比彈性梁的受載振動情況建立高超聲速飛行器縱向平面運動的彈性振動模型。

(2)

式中：W(x,t)是沿彈體分布的橫向載荷密度；y(x,t)表示彈體彈性振動,是沿彈體彈性坐標系ox軸的幅值時變函數;m(x)是彈體質量分布函數。以各階固有振型為基坐標,用固有振型線性表達式表示彈體彈性振動函數：

(3)

式中:ηi(t)為第i階振型對應的廣義坐標。利用固有振型的正交化進行化簡求解,得到彈性高超聲速飛行器振動的常微分方程：

(4)

式中：ωi為固有頻率;ζi為第i階彈性模態的阻尼比;Ni為第i階彈性模態的廣義力。聯立式(1)和式(4)即可得到高超聲速飛行器剛體-彈性耦合模型,其中彈性振動方程中只考慮一階彈性模態。

文中研究對象為巡航飛行的高超聲速飛行器,推力可認為是常量,升力、阻力、俯仰力矩和第一階彈性模態的廣義力可表示為:

(5)

式中:Sref、Lref分別為飛行器參考面積和參考長度;q為飛行器動壓,表達式為q=ρV2/2;δz為飛行器升降舵偏角;CY、CX、CMz、CN1分別為各力和力矩系數,擬合方程為:

(6)

1.2 高超聲速飛行器參數不確定問題

高超聲速飛行器飛行環境復雜,飛行過程中,飛行器的結構參數和氣動參數等均會產生明顯的攝動,表達式為:

(7)

式中:m0、Sref0、Lref0、Jz0為結構參數的基準值;CY、CX、CMz、CN1為氣動參數的基準值;Δm、ΔSref、ΔLref、ΔJz、ΔCY、ΔCX、ΔCMz、ΔCN1為其不確定性。

考慮飛行器結構參數和氣動參數攝動,可得簡化的面向控制的彈性高超聲速飛行器縱向動力學模型為:

(8)

(9)

式中:Δα、Δωz為上述近似以及氣動參數變化、結構參數變化引起的建模誤差,它們是攻角、俯仰角速度和升降舵偏角的非線性函數。

若分別記:

x1=α,x2=ωz,u=δz,Δ1=Δα,Δ2=Δωz

則簡化的彈性高超聲速飛行器縱向動力學模型可表示為如下的一般形式:

(10)

式中：Δ1是非匹配不確定部分;Δ2是匹配不確定部分。綜合考慮自適應滑模控制和反演控制在處理不確定系統時的優點,可以將兩種控制方法結合起來,設計彈性高超聲速飛行器控制律。

2 控制器設計

2.1 反演自適應滑模控制器設計

假設式(10)表示的系統中的匹配和非匹配不確定項都滿足不確定量有界條件:

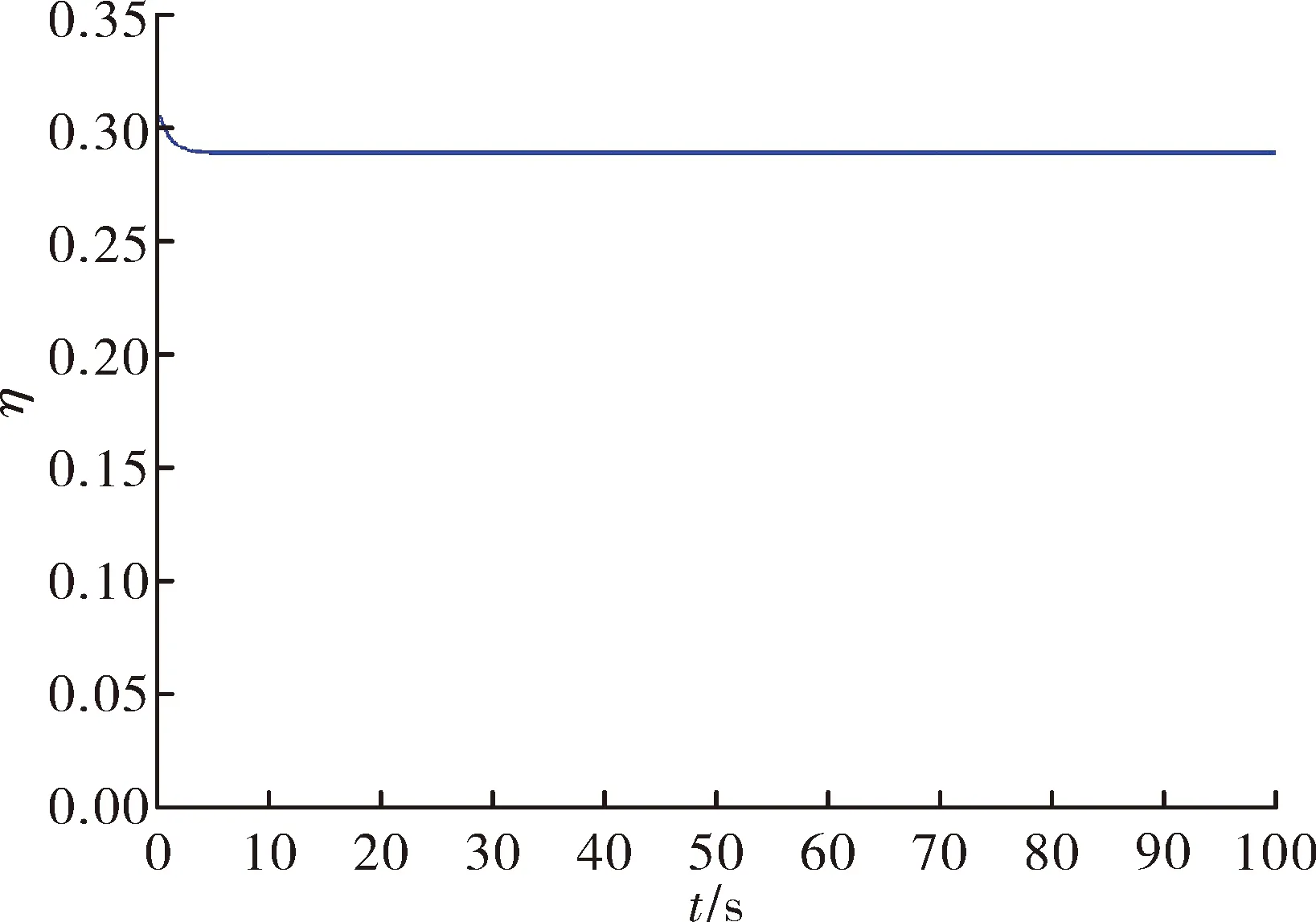
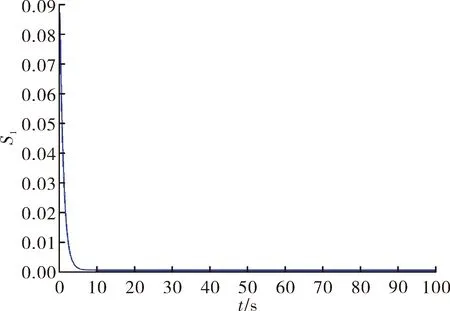
|Δ1|

式中:E1、E2是未知的正常數。

設攻角指令為x1d,需要設計跟蹤控制器使得x1→x1d。

第一步,為第一個狀態變量x1定義一個滑模面,如下所示:

S1=x1-x1d

(11)

根據式(10),對第一個滑模面S1求導:

(12)

將x2作為虛擬控制量x2d,選取滿足滑動模態可達條件的參數自適應調節的指數趨近律,使得:

x2d=-f1(x1)-g1(η)-k1S1-E1sgn(S1)

(13)

(14)

虛擬控制量x2d可調整為:

(15)

式中:k1>0,r1>0為常數。

令x2=x2d,將式(15)代入式(12),可得:

(16)

第二步,設計控制器以消除虛擬控制量x2d與狀態量x2之間的偏差。對第二個狀態量x2定義滑模面,以實現x2對虛擬控制量x2d的跟蹤:

S2=x2-x2d

(17)

根據式(12)、式(15)以及x2=S2+x2d,第一個滑模面的滑模運動方程(式(16))應改寫為如下形式:

(18)

同理,對滑模面S2求導可得:

(19)

同樣選取滿足滑動模態可達條件的指數趨近律,且飛行器飛行過程中有b≠0,可得設計的控制量u表達式如下:

(20)

式中：k2>0,r2>0為常數。

(21)

將控制量u的表達式式(20)代入式(19)可得滑模運動方程:

(22)

經過以上步驟即完成了彈性高超聲速飛行器縱向非匹配不確定系統的反演自適應滑模控制律設計:對于系統(10)設計式(15)、式(20)帶自適應項的滑模控制器,以使系統(10)的狀態穩定且能夠滿足控制要求,即x1→x1d。

2.2 穩定性證明

選用的李雅普諾夫函數為:

(23)

由定義可知V>0,對其進行求導可得:

(24)

由式(24)可得:

(25)

為了降低抖振,采用飽和函數代替符號函數可得：

其中:φ為邊界層厚度。

3 仿真驗證

3.1 仿真條件及參數設置

假設彈性高超聲速飛行器定高巡航飛行,令H0=25 000 m,V0=1 800 m/s。其他狀態量初始條件設定為:初始彈道傾角θ0=0°,初始攻角α0=5°,初始俯仰角速度ωz0=0°/s,攻角的期望值αd=0°,仿真時間設定為100 s。控制器參數設置分別為:k1=20,k2=5,r1=0.2,r2=0.1,φ=0.1。

3.2 仿真結果分析

在上述仿真條件下,利用文中設計的反演自適應滑模控制方法,進行彈性高超聲速飛行器巡航飛行仿真實驗,仿真結果如圖1～圖6所示。

圖1 飛行器攻角變化曲線

圖2 飛行器俯仰角速度變化曲線

圖3 飛行器升降舵偏變化曲線

圖4 飛行器彈性狀態變化曲線

圖5 攻角滑模面變化曲線

圖6 俯仰角速度滑模面變化曲線

從仿真結果圖1中可以看出,所設計的控制器能夠實現非匹配不確定下彈性高超聲速飛行器攻角的穩定有效跟蹤。圖2是俯仰角速度的響應曲線,可以看到俯仰角速度能夠快速達到動態穩定。圖3是飛行器控制量變化曲線,在仿真初始時刻,舵面的偏轉幅度較大,是由于氣動彈性模態引起的振動較大,需要利用舵面的偏轉有效抑制彈性的影響。從圖4中也可以看出彈性模態在初始時刻有較大變化,隨后彈性振動趨于平穩,而升降舵偏轉也趨于平穩。圖5和圖6是設計的兩個滑模面的變化曲線,可以看出攻角滑模面與俯仰角速度滑模面均可在有限時間內收斂到0。

4 結論

針對彈性高超聲速飛行器的參數不確定性問題,文中設計了一種反演自適應滑模控制器,并證明了系統全局漸近穩定。通過仿真證明了設計的控制器,能夠較好地跟蹤攻角指令且有效地抑制彈性及不確定的影響。