探究非自治—捕食者-兩互惠食餌模型的動力學行為

【摘 要】 捕食者-食餌系統是當前全球數學界數學生態學研究中的重要內容，特別是在綠色發展理念的引導下，全球都大力倡導節能減排、治理全球環境的時代背景下，捕食者-食餌系統已經開始廣泛受到國內外生態學家與數學家的重視。文章就對非自治—捕食者-兩互惠食餌模型的動力學行為進行了研究，希望能對相關人士的研究工作提供參考。

【關鍵詞】 非自治—捕食者;互惠食餌模型;動力學行為

“我們要建設的現代化是人與自然和諧共生的現代化。”當前，在綠色發展理念下，全球都大力倡導節能減排，希望能推進全球環境的治理，實現人與自然和諧共生。而要想實現這一目的，首先必須加強生態研究，推動形成人與自然和諧發展的現代化建設新格局。在生態學中，最受人們關注的問題就是物種多樣性問題，而在物種多樣性問題中，物種的共存以及持續性生存問題是其重要的組成部分。目前，隨著人們對地球生物圈開發力度的加大，很多物種逐漸成為瀕危物種，甚至一部分永久消失了，為了保持地球生物物種的多樣化，實現人與自然的和諧共生，研究非自治—捕食者-兩互惠食餌模型的動力學行為就變得十分重要且十分緊迫。

一、數學生態學簡析

數學生態學是一門研究數學與生物學的交叉學科，這一學科是借助數學相關的知識、理論和方法去描述、分析并解釋自然生態環境中的一些生態現象、生態問題，從而探索出相應的生物學問題。在該學科的研究中，探索的方式方法有很多種，但目前最常用的就是借助數學知識、理論和方法構建相應的生態模型，把原本復雜的生物種群關系轉化為數學模型，然后借助相應的數學知識和理論對其動力學行為進行分析。通過這樣的研究，能有效促進生態學理論的順利發展，對于當前構建人與自然和諧共生的生態系統具有廣泛的實際應用價值。

該學科最早出現于二十世紀二十年代中葉，是由意大利數學家Volterra和生物學家Dancona在研究地中海魚類時提出來的。這二人在研究中發現，一戰前后，地中海地區的漁民捕獲的掠肉類魚種比例大幅度上升，而食用魚的比例相應下降。為了更好地解釋這一現象，二人對這兩大種類的魚捕食與被捕食關系進行了探究，第二年，美國數學家Lotka也提出了同樣的問題。因此，Lotka和Volterra將捕食者與食餌的關系轉化成了數學模型，從而形成了著名的Lotka-Volterra模型：，i=1，2…，n。

這一模型可以描述出不同物種種群之間的三種生存關系：一是競爭關系，如農作物和雜草爭奪陽光和養分;二是捕食食餌關系，如非洲大草原上獅子、獵豹等捕食角馬;三是互惠互存關系，如犀牛和犀牛鳥、螞蟻和蚜蟲、寄居蟹和海螺等。Lotka-Volterra模型的提出吸引了全球眾多的數學家和生物學家，很多學者在這一模型的基礎上進行了進一步研究并對相關理論進行了改進，延伸出了眾多的生物數學模型。在實際的生態環境中，不同物種之間的生存關系并不是單一存在的，而是同時存在著更為復雜的關系，即不同物種之間的生存關系是一種復雜多變的關系，可能同時存在著兩種或三種生存關系。要想建立確定性的模型來解決生物學中的問題，應該運用大數定律，從而建立比較穩定狀態的數學模型。而本文探究的就是一種捕食者捕食兩種存在著互惠互存關系的食餌。其模型如下：

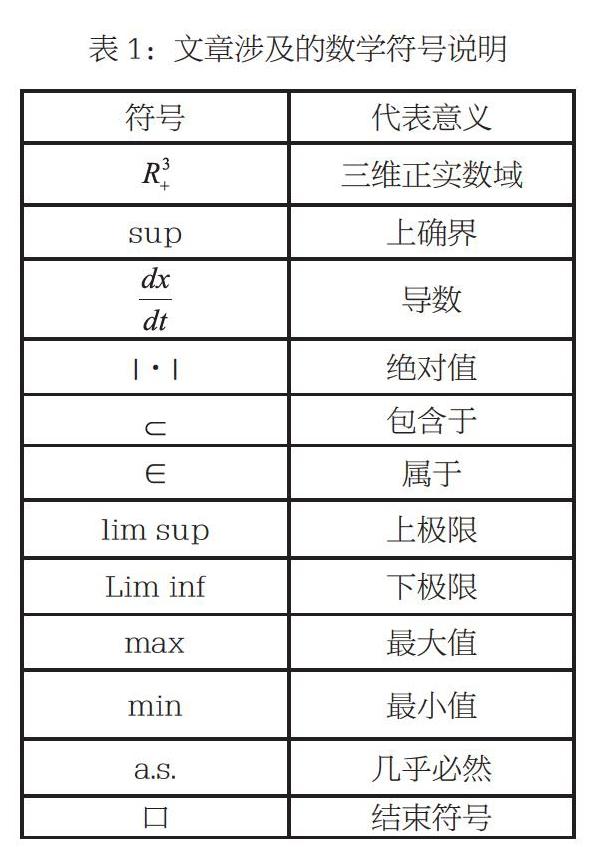
模型中的xi（t）代表的是在t時刻食餌種群的密度值;y（t）則是在t時刻捕食者種群的密度值;而其他系數a1（t）、b1（t）、c1（t）、d1（t）、D1（t）、e（t）、f（t）（i=1，2，t≥0）都是連續、有界、嚴格正的函數。為了更好地探究其生物學意義，研究其動力學行為，運用微分方程對其原理和構造進行系統討論。其中，文章涉及的符號代表意義見表1。

二、非自治—捕食者-兩互惠食餌模型的動力學行為分析

是本系統的正不變集。當xi（t0）>0時，則xi（t）>0，y（t）>0（i=1，2），因此，本系統滿足正初值的就能夠保持恒正。所以集合R是本系統的正不變集。如果本生態系統中始終存在著一個緊區域D∈Int，使得本系統的任何滿足正初始值條件（1，2）的解（xi（t），x2（t），y（t））都能最終進入并保留在緊區域D內，這樣本系統就能保持一致持久性。

適當選取m=min|m1，m2，n|≤M=|M1，M2，N1，并且m，M都不依賴系統（1，1）的任何正解，且本系統是一致持久的，對于生態系統（1，1），如果對于任何正解（xi（t），x2（t），y（t）），都有既能滿足Liapunov意義下的穩定，又對其他正解（xi（t），x2（t），y（t）），有，則可以將本系統看作是全局漸進穩定的。但在實際生活中，即真實的自然環境中，生物數學模型中的參數會受到各種各樣不同形式因素的影響，本文并沒有對這些影響因素對該物種的擾動進行探討，只是基于一種理想型的情形進行了簡單探討，因此還存在一定的不足。

綜上所述，非自治—捕食者-兩互惠食餌模型的動力學行為在自然界中十分普遍，本文就對這種模型在理性狀態下的持續性和正解全局漸進穩定性進行了探討，可能還存在一定的不足，但希望能為相關人士的進一步深入研究提供參考。

【參考文獻】

[1]蒲武軍，杜爭光.一類分數階廣義捕食者-食餌模型的動力學分析[J].西北師范大學學報（自然科學版），2018（05）：14-19.

[2]梁桂珍，宋鴿.一類具有Machaelis-Menten型功能性反應的非自治兩捕食者-兩競爭食餌的系統的持久性與穩定性[J].數學的實踐與認識，2018（21）：290-296.

【簡介：李艷，女，新疆烏魯木齊人，1972年5月，學歷：本科，職稱：新疆建設職業技術學院講師，研究方向：微分方程方向】