ARIMA模型與指數平滑法在新冠肺炎疫情傳播中的應用

盧普慶

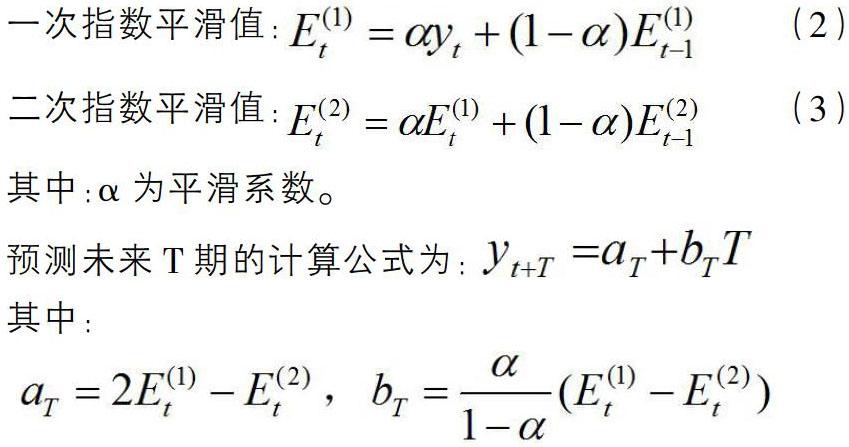
摘要：目的：分析ARIMA模型和指數平滑法對我國新型冠狀肺炎（COVID-19）疫情變化趨勢的預測效能。方法：選取我國2020年1月10日-2020年4月20日新冠肺炎累計確診病例數作為ARIMA模型和指數平滑法的建模部分，2020年4月21日-2020年4月30日數據作為模型驗證部分，比較兩種模型的擬合情況和預測效果優劣。結果：ARIMA（2，2，1）模型的均方誤差根（RMSE）為301.9043，相對誤差百分比（REP）為3.1743，指數平滑模型的RMSE為200.9823，REP為2.1306。結論：指數平滑模型擬合效果較好，預測精度更高，可應用于我國COVID-19累計確診病例數的預測。

Abstract： Objective： To analyze the predictive power of the ARIMA model and exponential smoothing method for the trend of COVID-19 in China. Methods： The cumulative number of newly diagnosed cases of new coronary pneumonia in China from January 10， 2020 to April 20， 2020 was selected as the modeling part of the ARIMA model and exponential smoothing method， and the data from April 21， 2020 to April 30， 2020 was used as the model In the verification part， compare the fitting situation of the two models and the pros and cons of the prediction effect. Results： The root mean square error （RMSE） of the ARIMA （2，2，1） model was 301.9043， the relative error percentage （REP） was 3.1743， the RMSE of the exponential smoothing model was 200.9823， and the REP was 2.1306. Conclusion： The exponential smoothing model has a better fitting effect and higher prediction accuracy， and can be used to predict the cumulative number of confirmed cases of COVID-19 in China.

關鍵詞：新型冠狀肺炎;ARIMA模型;指數平滑法;預測

Key words： COVID-19;ARIMA model;exponential smoothing method;prediction

中圖分類號：N32? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1006-4311（2020）23-0164-04

0? 引言

自2019年12月底在湖北省武漢市發現新型冠狀病毒肺炎病例以來，新冠肺炎迅速在全球流行。2020年1月12日世界衛生組織（WHO）將該病毒命名為2019-nCoV[1]， 2月11日世界衛生組織（WHO）將該病毒引起的疾病正式命名為COVID-19（Corona virus disease 2019）[2]，3月11日，世界衛生組織正式宣布此次疫情為世界大流行，防控工作已成為全球公共衛生共同關注的問題。截止5月1日24時，COVID-19已影響到全球212個國家和地區，累計確診病例逾300萬，累計死亡已超過23萬。絕大多數國家目前疫情仍在持續增長階段，沒有達到有效控制。而我國疫情在精準施策，科學防控等一系列措施下，取得了階段性勝利，目前以境外輸入性病例為主。疫情防控的成功與對病毒傳播趨勢的了解密不可分。因此，構建新冠肺炎疫情變化趨勢的有效預測模型，對新冠肺炎疫情的防控具有重要的現實意義。

1? 文獻綜述

目前，針對新冠肺炎防控的相關研究，主要可以分為三個方面：一是基于參數和建模的研究：尹楠（2020）[3]應用標準流行病學SIR倉室模型，對此次新冠肺炎疫情中的幾種感染情況做了仿真研究，并根據研究結果提出了一些控制疫情蔓延的措施和方法。Yang Zi-feng（2020）[4]結合經典SIR倉室模型和SEIR倉室模型，以多重擬合確定模型參數，對疫情趨勢做了預測研究，在參數估計方面更接近實際。顏銘江等（2020）[5]改進了傳統SEIR模型中僅考慮確診病例存在傳染性而潛伏期病例無傳染性這一缺陷，提出了新模型（ISEIR），應用ISEIR模型預測了今后疫情的進一步發展趨勢。二是基于疫情防控措施效果評估的研究：陳端兵等（2020）[6]以有效再生數作為評價防控措施的核心指標，計算并反推了患者癥狀的出現時間，發現切斷本地傳播源、實施交通管制等舉措有顯著成效。MOORE（2020）[7]基于目標函數法，研究了自我防控、初期診斷治療和末期診斷治療三種防控措施分別實施和組合實施下的疫情傳播速度，結果指出三種防控措施組合效果更好。三是基于臨床醫學和藥理學的研究：楊小林、袁永亮等（2020）[8]采用ETCM、中藥系統藥理學分析平臺（TCMSP），分析得到升降復方靶蛋白基因，結果表明升降散對新冠肺炎具有潛在抑制作用。

上述研究為新冠肺炎的防控提拱了寶貴意見，也為本文提供了啟發。基于統計學視角，將我國新冠肺炎累計確診病例隨時間變化而變化的數據看成一組時間序列。采用ARIMA模型和指數平滑法對數據進行分析，建立ARIMA模型和指數平滑模型，并通過實證研究來評價兩種模型的預測效能，從而確定最優預測模型，為將來我國新冠肺炎疫情防控工作提供參考依據，也為其他新冠肺炎疫情研究提供借鑒。

2? 資料與方法

2.1 數據來源及假設

2020年1月10日-2020年4月30日我國COVID-19累計確診病例數來源于國家衛生健康委員會疫情通報。這里做個基本假定：國家衛建委于2020年1月21日通報全國新冠肺炎疫情情況，1月10日-1月20日無全國累計確診病例數，由于疫情重災區位于湖北省武漢市，故假定武漢市1月10日-1月20日累計確診病例數為全國累計確診病例數。

2.2 研究方法

2.2.1 ARIMA模型全稱為自回歸移動平均模型，由美國George Box和英國Gwilym Jenkins于20世紀70年代初共同建立。ARIMA模型定義為[9]：

2.2.2 指數平滑法是由（Robert G. Brown）提出的一種基于移動平均法，改進而來的時間序列分析方法。指數平滑法在流行性傳染病發病率預測中的應用已十分廣泛，如流感樣病例等[10]。指數平滑法彌補了移動平均法的不足，充分利用了所有數據信息，又體現出近期數據對未來影響作用更大的特點。根據時間序列是否具有季節性，可分為季節性模型（季節指數平滑法、Holt-Winter加法指數平滑法、Holt-Winter乘法指數平滑法）和非季節性模型（一次指數平滑法、二次指數平滑法）[11]，其中一次指數平滑法主要應用于沒有趨勢的季節性的序列，二次指數平滑法主要應用于有趨勢但沒有季節性的序列。根據我國新冠肺炎累計確診病例數據的變化趨勢，本文選擇二次指數平滑模型，其公式為：

2.2.3 分析方法 本研究采用SPSS 23.0，將1月10日-4月20日我國新冠肺炎累計確診病例數作為建模部分， 4月21日-4月30日數據作為模型驗證部分。選取二次指數平滑模型中的簡單線性趨勢模型、Holt線性趨勢模型、Brown線性趨勢模型依次擬合三種模型，依據確定系數R2最大、均方誤差平方根（RMSE）、平均絕對誤差百分比（MAPE）和平均絕對誤差（MAE）最小確定最優模型[12]。

3? 結果

3.1 我國COVID-19累計確診病例數分布特征

對我國1月10日-4月30日新冠肺炎累計確診病例數進行分析，觀察累計確診病例數時間序列圖，可見累計確診病例數總體呈明顯上升趨勢，且無明顯季節性和周期性。

3.2 ARIMA模型建立

3.2.1 平穩性檢驗

對原始序列做單位根檢驗，根據結果可知，原始序列非平穩，對其一次差分后做單位根檢驗，P>0.001，進而二次差分，顯示序列平穩。

3.2.2 ARIMA模型識別

觀察二次差分后序列的自相關函數圖（AC）和偏自相關函數圖（PAC）可知，AC和PAC圖存在明顯拖尾性，且AC圖一階截尾，故q=1，由PAC圖可知，p取2或3。根據可決系數（R2）、調整的可決系數、赤池信息準則（AIC）以及施瓦茲準則（SC）可得，p取2。綜合上述分析可知，確定模型為ARIMA（2，2，1）。

3.2.3 ARIMA模型檢驗

根據ARIMA（2，2，1）模型做回歸，并對其殘差序列進行白噪聲檢驗，由殘差序列的AC圖、PAC圖以及p值可知，殘差序列不存在自相關，且滿足零均值，為白噪聲序列，故認為其通過檢驗。

3.2.4 模型預測

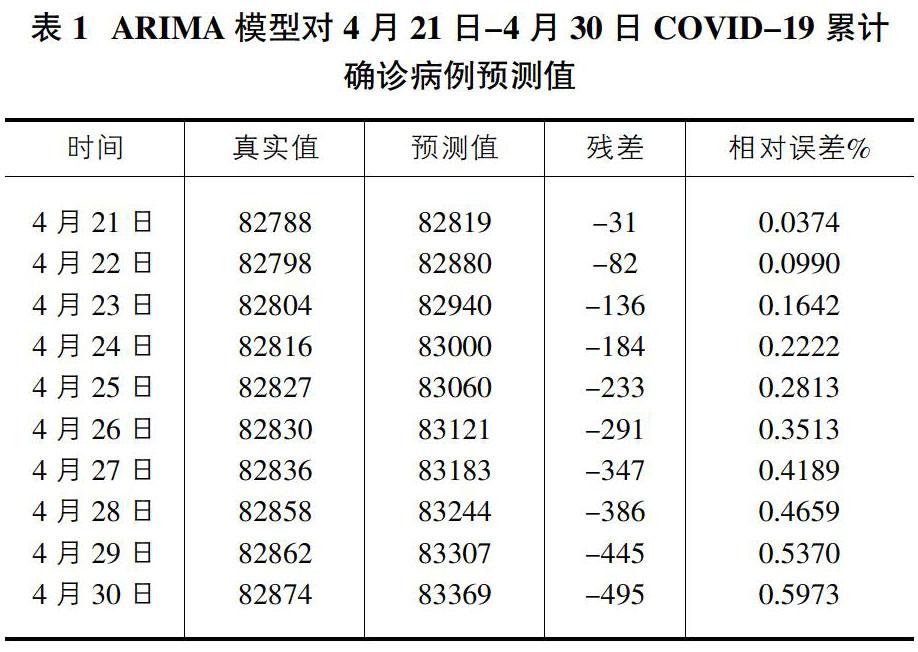
利用ARIMA（2，2，1）模型對我國4月21日-4月30日新冠肺炎累計確診病例做預測，并于實際值進行對比，結果如表1。

3.3 指數平滑法

3.3.1 構建模型

根據我國COVID-19累計確診病例數時序圖，初步選擇指數平滑模型中的簡單模型、Holt線性趨勢模型和Brown線性趨勢模型，分別對我國1月10日-4月20日新冠肺炎累計確診病例數進行擬合，模型擬合結果見表2。

根據表3可知，Brown線性趨勢模型的最大，且RMSE、MAPE、MAE以及正態化BIC值最小，因此，選擇Brown線性趨勢模型對COVID-19累計確診病例數進行擬合，擬合情況見圖1。

3.3.2 指數平滑模型預測結果

運用指數平滑模型中的Brown趨勢模型對我國新冠肺炎累計確診病例數進行預測，擬合預測曲線圖見圖2，預測結果見表3。

3.3.3 ARIMA模型和指數平滑模型比較

為了更好的對兩個模型的預測精度進行對比分析，本文引入均方根誤差（RMSE）和相對誤差百分比（REP）兩種度量指標，相應度量指標定義如下：

根據表4可知，指數平滑模型的RMSE值和REP值均小于ARIMA模型，因此，指數平滑模型預測效果更好。

4? 討論

ARIMA模型和指數平滑模型均是通過探索歷史數據隨時間變化而變化的某種規律，并將這種規律進行外延，來預測將來情況。兩種模型均適合于中短期預測。ARIMA模型比較全面的考慮了序列的長期趨勢、季節變動、循環變動以及不規則變動等情況，并結合模型參數對其進行了量化，能較好的反映時間序列的變化和趨勢[13]。但ARIMA模型的建模過程相對復雜，模型參數的識別存在一定主觀性。指數平滑法則需要反復運算，以確定最優平滑系數，其基本思想是給近期數據賦予更大的權重，而遠期數據賦予較小權重，適合于序列隨時間變化不大的數據。因此，兩種模型均有一定局限性，在不同條件下，應結合具體情況而定。

本文采用ARIMA（2，2，1）模型和指數平滑模型對我國新冠肺炎累計確診病例數進行了預測，研究結果表明，ARIMA（2，2，1）模型的均方誤差根（RMSE）為301.9043，相對誤差百分比（REP）為3.1743，指數平滑模型的RMSE為200.9823，REP為2.1306，均小于ARIMA（2，2，1）模型，且指數平滑模型預測結果與國家衛健委疫情通報結果基本吻合。因此，指數平滑模型更適合于我國新冠肺炎累計確診病例的短期預測。

參考文獻：

[1]武漢市衛生健康委員會通報：1月13日無新增新型冠狀病毒感染的肺炎病例，中國發展網，2020，1，15.http：www.chinadevelopment.com.cn/sh/2020/0115/1601245.shtml.

[2]世界衛生組織給新冠病毒命名，新京報，2020，2，12.http//news.sina.com.cn/w/2020-02-12/doc-iimxxstf0768050.shtml.

[3]尹楠.基于SIR模型的有限區域內新冠肺炎疫情傳播仿真模擬[J].統計與決策，2020（5）.

[4]Yang Zi-feng， Zeng Zhi-qi， Wang Ke， et al. Modified SEIR and AI? ?prediction of the epidemics trend of COVID-19 in China under public Health interventions[J].Journal of Thoracic Disease，2020，doi：10.2103/jtd.2020.0264.

[5]顏銘江，董一鴻，賈香恩，鄭海陽，辛宇.新型冠狀病毒肺炎的疫情趨勢預測[J/OL].病毒學報：1-10[2020-4-30].http：//kns.cnki.net/kcms/detail/11.1865.r.20200429.1658.004.html.

[6]陳端兵，白薇，王巖，王敏，俞伍平，周濤.新型冠狀病毒肺炎防控效果的定量評估[J/OL].電子科技大學學報：1-6[2020-3-31].http：//kns.cnki.net/kcms/detail/51.1207.T.2020.330.1149.002.html.

[7]MOORE S E， OKYERE E. Controlling the Transmission Dynamics of COVID-19[J/OL].arXiv：2004.00443v2[q-bio.PE].[2020-04-02].http：//arXiv.org/abs/2004.00443.

[8]楊小林，袁永亮，張杰，王如鋒，倪力強.基于網絡藥理學和分子對接探尋升降散對抗新型冠狀病毒潛在作用機制研究[J/OL].中草藥，2020，51（7）：1795-1803.

[9]Box G E P. Jenkins G M. Time Series Analysis： Forecasting and Control[M]. 4 th ed New Jersey： Hoboken，2011.

[10]孔德川，潘浩，鄭雅旭，等.指數平滑模型在上海猩紅熱發病率預測中的應用[J].疾病檢測，2019，34（10）：932-936.

[11]P. R. A Firmino， P S de Mattos Neto， Tiago T. E Ferreira. Correcting and Combining time series forecasters[J]. Neural Networks，2014，50：1-11.

[12]顧蓉艷，張玲，宋肖肖，等.基于季節性指數平滑法的學校因病缺課預測研究[J].中華疾病控制雜志，2019，23（7）：845-855.

[13]王春平，王志峰，單杰，等.隨機時間序列分析方法在傳染病預測中的應用[J].中國醫院統計，2006，13（3）：229-232.