火星大氣進入段抗飽和固定時間阻力加速度跟蹤制導律設計*

龔有敏，郭延寧，馬廣富，高新洲

(哈爾濱工業大學 控制科學與工程系·哈爾濱·150001)

0 引 言

隨著航天技術的不斷發展，人們對于深空的探索欲與好奇心不斷驅使著各個國家和組織前赴后繼地開展各種深空探索活動。在八大行星中，火星距離地球最近，生存環境與地球最為類似。人類一直寄希望于火星能夠給生命提供生存條件，作為人類可持續發展的基地。因此，各個國家將火星探測作為現在深空探測的主要方向之一，火星探測技術引領著深空探測技術不斷發展[1-2]。1962年11月1日，蘇聯的“火星1號”揭開了火星探測的序幕。迄今為止，共有6個國家和組織進行了46次探測火星的嘗試[3]，從著陸精度為150km的“火星探路者”到10km著陸精度量級的“火星科學實驗室”，火星探測器的著陸精度越來越高，而未來火星探測任務對精度的需求也越來越高，這無疑給火星探測技術帶來了很多機遇與挑戰[4]。

火星探測器從脫離火星繞飛軌道進入火星大氣開始，一般包括大氣進入段、下降段和著陸段三個(Entry，Descent and Landing，EDL)階段[5]。大氣進入段為火星探測器著陸整體任務中的第一階段。由于火星大氣稀薄，在進入過程中火星大氣能夠提供給探測器的氣動力非常有限，使得依靠氣動力修正不確定性和外界干擾帶來的進入誤差成為進入段制導的一大難題，同時進入段的精度也直接影響著后續的著陸精度[3,6]。

目前，研究火星探測器在大氣進入段的制導方法主要包括了預測—修正制導和跟蹤制導[7-10]兩大類。預測—修正制導的關鍵之處是參數建模、約束條件和求解方法。為了滿足在線求解的快速性、穩定性與收斂性，需要進行簡化處理，這就在一定程度上限制了預測—修正制導的使用。相關研究包括，李毛毛等[11]根據一階特征模型設計的全系數自適應預測修正制導律，利用時變動態增益變換技術降低了預測誤差與制導修正量之間的時變動態增益，并給出了全系數自適應預測修正制導律的收斂性證明。夏元清等[12]詳細介紹了預測—修正制導，給出了增加檢測點的改進預測制導律。Zheng等[13]在性能指標中加入了光滑處理的精確懲罰函數來設計制導律。該方法無需額外的假設或處理，便能得到穩定的求解，但經驗對其具有較大的影響。跟蹤制導通常基于阻力加速度跟蹤設計制導律，如Furfaro等[14]設計了在有限擾動下的全局穩定多滑模制導律，Dai等[15]利用終端滑模設計了縱向運動的有限時間制導律，閆曉鵬等[16]利用齊次性方法結合干擾觀測器設計了有限時制導律。但是，跟蹤制導在初始跟蹤誤差較大時容易出現飽和且存在跟蹤誤差難以消除的情況。

火星探測器大氣進入段的橫向運動與縱向運動是能夠實現解耦設計的。通常都是利用縱向運動設計制導律，再通過傾側角反號完成橫向制導。目前橫程和航向角常用于設計傾側角反號邏輯，Lu等[17]利用速度設計了二次型的橫程閾值，進行傾側角切換。郭敏文和Christopher W等[18-19]設計了速度的線性函數作為橫程閾值。利用橫程閾值設計的傾側角邏輯計算相對復雜且計算量大，增加了宇航計算機的運算壓力。夏元清等[12]利用反饋線性化方法將航向角誤差選為一階慣性環節設計反號邏輯。趙振華等[20]將航向角誤差閾值設計為常值進行傾側角的切換。該方法在起始速度較大時易發生傾側角的頻繁反號，從而導致任務失敗。

本文研究了阻力加速度的跟蹤制導方法。在橫向運動中，給出了與速度成線性關系的航向角誤差漏斗走廊并設計了傾側角反號邏輯。與傳統的橫程漏斗走廊相比，該方法計算簡單。與航向角誤差等寬走廊相比，該方法能夠有效減少大速度情況下的傾側角符號切換，提高任務成功概率。在縱向運動中，考慮到RBF神經網絡對非線性具有很好的逼近作用，本文通過RBF神經網絡補償了傾側角的飽和問題，結合固定時間控制理論，設計了縱向固定時間阻力加速度跟蹤滑模制導律，使得跟蹤誤差可在有限時間內收斂至0。考慮到滑模控制具有強魯棒性且積分滑模能夠解決傳統滑模控制的抖振問題，本文利用跟蹤誤差設計了積分形式的滑模面，并將跟蹤誤差以兩種不同的形式引入制導律。這種方法一方面能夠有效消除抖振，另一方面也能保證在誤差較大與較小時均可加快收斂速度。通過數值仿真，驗證了本文所設計的橫向傾側角切換邏輯與縱向制導律在大氣進入段的有效性，且確保了較高的跟蹤精度。

1 大氣進入段動力學與問題分析

1.1 大氣進入段動力學模型

火星探測器在大氣進入段是無動力飛行的，可通過改變傾側角達到改變探測器位置和速度的目的。將探測器視為質點，可建立探測器的動力學方程如下：

(1)

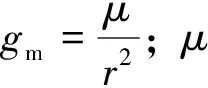
(2)

L=ρV2CLS/(2m)

(3)

式中，m為探測器質量；S為探測器參考表面積；CL和CD分別為火星大氣的升力系數和阻力系數；Bf為探測器的彈道系數；ρ為火星大氣密度，定義為如下參考高度rs的函數：

ρ(r)=ρsexp[-β(r-rs)]

(4)

式中，ρs為參考高度處的大氣密度；rs為參考高度；β為參考高度的倒數。

1.2 問題分析

火星探測器在大氣進入段通過改變傾側角σ達到改變位置和速度的目的，因此大氣進入段的制導律設計即為確定合適的傾側角σ的變化規律，以滿足任務要求，完成對標稱大氣進入軌跡的跟蹤。

由動力學方程(1)可以看出，在大氣進入段，探測器的縱向運動和橫向運動是解耦的。針對縱向運動所設計的傾側角σ，可以通過改變其符號改變橫向運動，而確保縱向運動不受影響。因此，本文僅針對縱向運動設計制導律，橫向制導通過設計合理的反號邏輯對σ反號即可。

2 制導律設計

2.1 橫向傾側角反號邏輯設計

探測器在大氣進入段中，為確保探測器的精確著陸，要求大氣進入段的末端具有較高的進入精度，即大氣進入段不僅要保證縱向運動的精度，還需要保證橫向運動的精度，而橫向運動的誤差可通過改變傾側角的符號而實現。為此，需要合理地設計傾側角的反號邏輯，以達到橫向運動的精度要求。

本文利用航向角誤差進行傾側角反號邏輯設計，定義航向角誤差為

eψ=ψ-ψd

(5)

其中，ψd為期望的航向角。

通過限制航向角誤差，在某一滿足橫向運動精度要求的范圍內保證橫向運動的精度。當航向角誤差超出該閾值，傾側角σ反號，使得航向角向減小誤差的方向運動，進而保證橫向運動的精度。

為了保證橫向運動精度且避免傾側角頻繁切換，本文利用探測器的速度V設計了航向角誤差的閾值，該閾值設計為速度的線性函數：

|ζ|=η1V+η2

(6)

式中，η1和η2為常系數，可根據任務要求進行選取。

式(6)描述的航向角誤差閾值為漏斗走廊形式，該閾值走廊在進入段起始階段探測器速度較大時，閾值相應也較大，航向角誤差不會因此頻繁到達閾值邊界而引起傾側角頻繁反號，進而可減少傾側角切換的次數。當進入大氣進入段末端時，探測器的速度較小，此時航向角誤差的閾值也相應較小，能夠限制航向角誤差在較小的范圍內，進而保證橫向運動的精度。根據任務需求，合理地選取η1和η2，不僅能夠保證橫向運動的末端精度，還能減少傾側角反號的頻率。

2.2 抗飽和固定時間縱向制導律設計

2.2.1 阻力加速度數學模型推導

從阻力加速度D的表達式(2)可以看出，阻力加速度D并不顯含傾側角σ，而是與速度V相關。結合動力學方程(1)可知，在D的二階導數中會出現傾側角σ。基于阻力加速度的跟蹤制導律設計其實研究的就是阻力加速度的變化規律。通過設計相應的傾側角σ，完成對期望阻力加速度的跟蹤，進而實現對火心距r、速度V、經度θ、緯度φ等的跟蹤。

對阻力加速度求一階導可得

(7)

進一步對式(7)求導可得

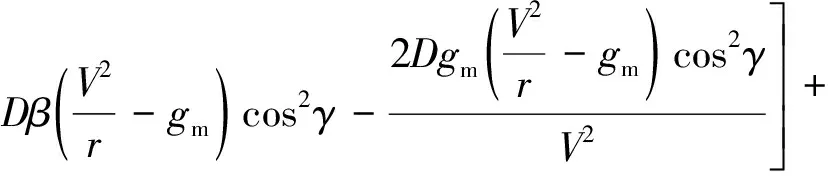
=f(x)+g(x)u

(8)

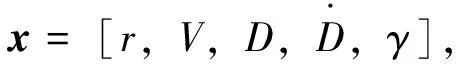
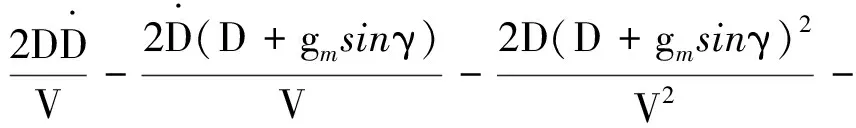
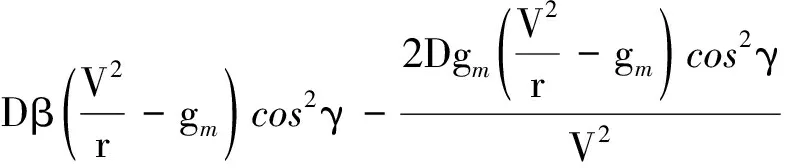
(9)

(10)

2.2.2 制導律設計

針對式(7)和式(8)，設計縱向制導律u。在設計之前，先給出兩個引理：

引理1[21]：考慮系統(11)，若在平衡點的鄰域U?Rn內存在Lyapunov函數Vb(x3)滿足條件(12)，則系統(11)是在固定時間內穩定到平衡點的，且對于任意的Vb(x3)都能夠在固定的時間Tb收斂到0。收斂的時間Tb與初始狀態有關且存在上界，滿足式(13)。其中，常數α,λ,p,k>0，pk<1且gk>1。

(11)

(12)

(13)

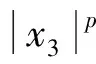
(14)

結合式(7)和式(8)，得到阻力加速度跟蹤誤差模型如下：

(15)

考慮到探測器的傾側角存在飽和，即

u=sat(u)+δ

(16)

式中，u為理想制導律輸出，sat(u)為制導律的輸出，δ=u-sat(u)為控制偏差，sat(u)的定義如下：

(17)

式中，umax為制導律的飽和值。

此時式(15)可改寫為

(18)

利用RBF神經網絡對g(x)δ進行逼近，由RBF神經網絡逼近原理[23]，可給出以下假設。

假設1：對于?εN>0，存在最優加權矩陣θ*，使得RBF神經網絡的逼近誤差滿足

(19)

其中，Φ(x)為高斯RBF函數。

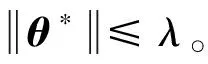
RBF神經網絡對g(x)δ的估計為

(20)

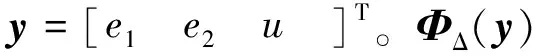
(21)

其中，ξi∈Rn,μi>0為第i個高斯RBF函數的中心和寬度。

為避免滑模控制固有的抖振問題，選取基于跟蹤誤差的積分滑模面

(22)

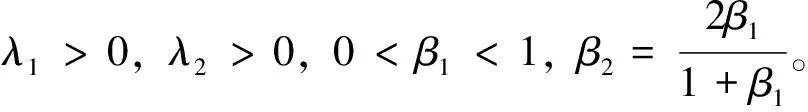
定理1：利用式(22)所設計的固定時間跟蹤制導律(23)，式(18)中的火星探測器大氣進入段阻力加速度跟蹤誤差可在固定時間內收斂到滑模面，即s=0。然后，系統狀態可在有限時間收斂到平衡點，即e1=e2=0，且收斂到滑模面的時間滿足式(24)

u=g-1(x){[-f(x)-λ1sigβ1(e1)-

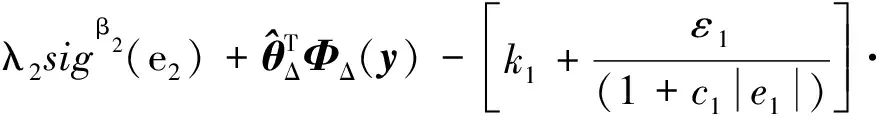
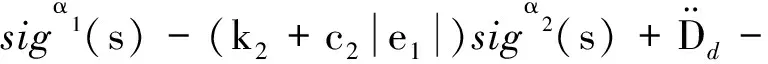
k3sgn(s)}

(23)

式中，控制增益k1>0，k2>0，c1>0，c2>0，ε1>0，0<α1<1，α2>1，k3>εN。

(24)

RBF神經網絡自適應律為

(25)

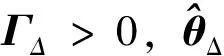
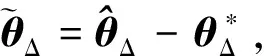
(26)

對式(26)求導得

=s(λ1sigβ1(e1)+λ2sigβ2(e2)+f(x)-

sg(x)δ+sθ*ΦΔ

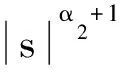
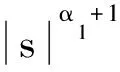
(27)

根據引理1得證，跟蹤誤差在固定時間內收斂到式(22)的滑模面。

到達滑模面后，系統變為

(28)

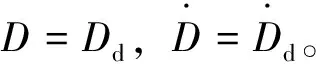
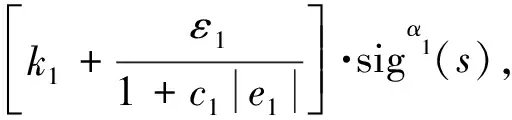
3 數值仿真與分析

為驗證本文所設計的橫向傾側角反號邏輯和縱向制導律的有效性，采用文獻[24]的參數生成標稱軌跡設計仿真實驗并進行驗證，生成標稱軌跡的探測器參數如表1所示。

表1 標稱系統參數

生成大氣進入段標稱軌跡的傾側角滿足：

σ=

(29)

為了驗證所設計制導律對于初始跟蹤誤差的不敏感性，選取的實際探測器的初始參數與標稱系統稍有區別，如表2所示。制導律參數如表3所示。

表2 探測器實際參數

表3 本文制導律參數及PD制導律參數

為了對比本文所設計的制導律的優越性，采用與本文相同的傾側角符號切換邏輯，并采用如下PD制導律：

u=g-1(x)[-f(x)-k4e1-k5e2]

(30)

利用計算機進行數值仿真驗證，可得仿真結果如圖1～圖16所示。

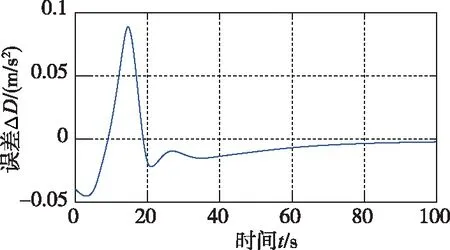
圖1 本文制導律阻力加速度跟蹤誤差

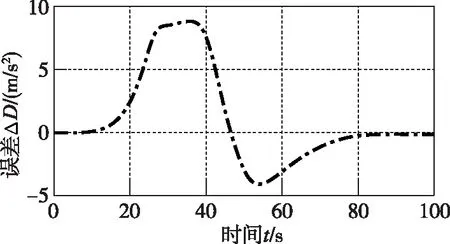
圖2 PD制導律阻力加速度變化率跟蹤誤差

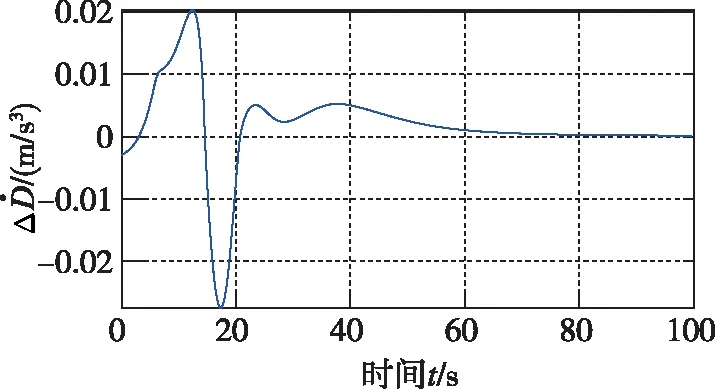
圖3 本文制導律阻力加速度變化率跟蹤誤差

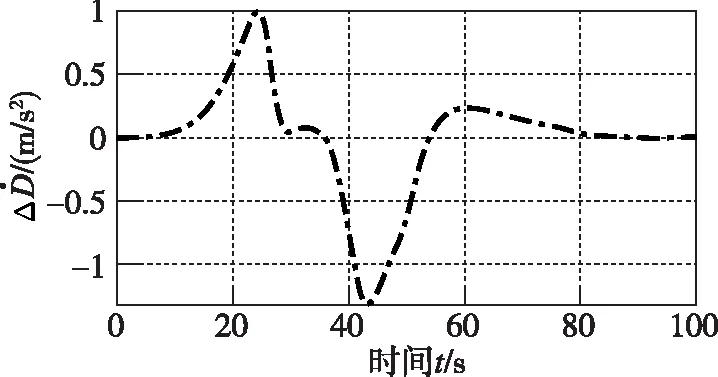
圖4 PD制導律阻力加速度變化率跟蹤誤差

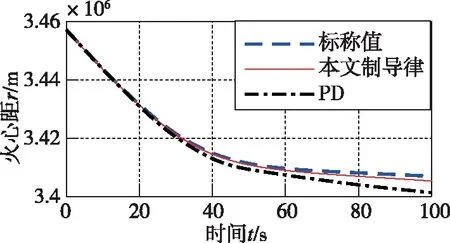
圖5 火心距跟蹤曲線

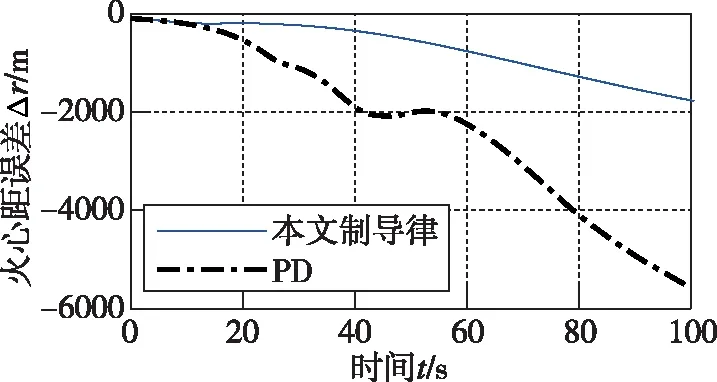
圖6 火心距跟蹤誤差

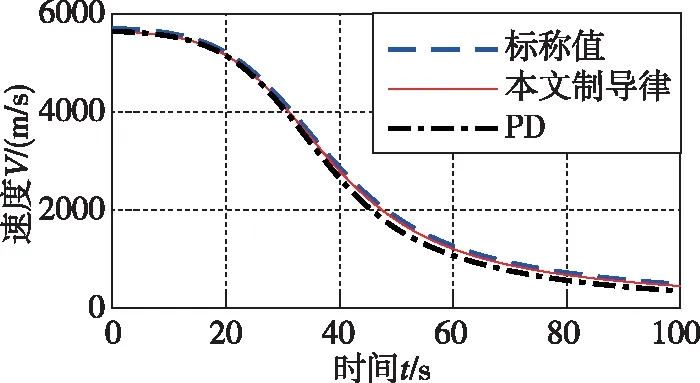
圖7 速度跟蹤曲線

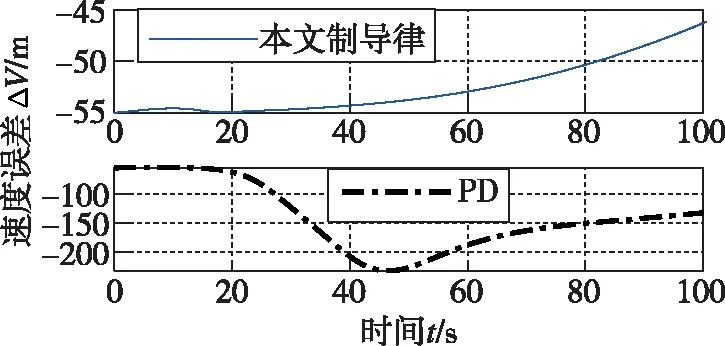
圖8 速度跟蹤誤差

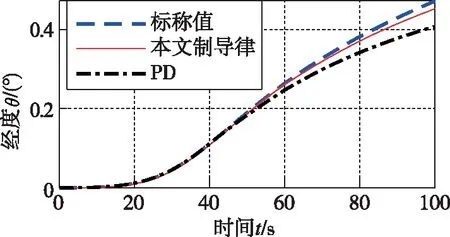
圖9 經度跟蹤曲線

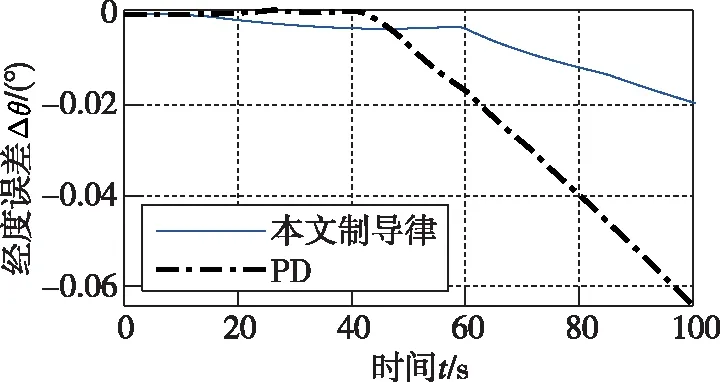
圖10 經度跟蹤誤差

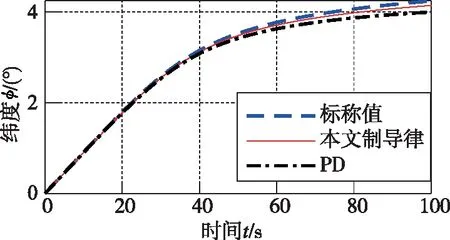
圖11 緯度跟蹤曲線

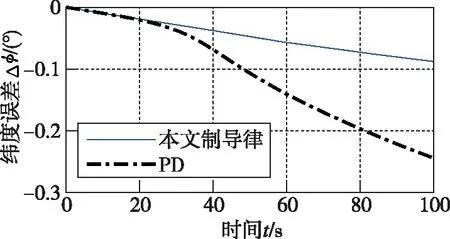
圖12 緯度跟蹤誤差

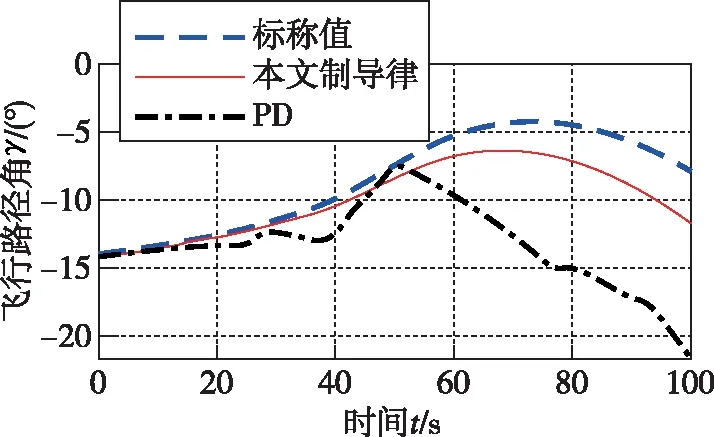
圖13 飛行路徑角跟蹤曲線

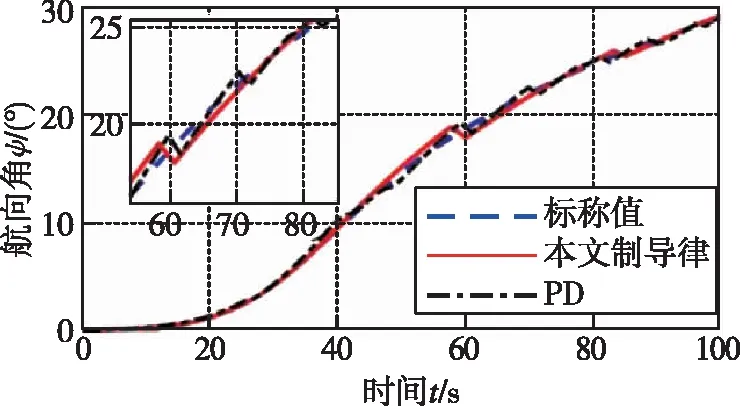
圖14 航向角跟蹤曲線

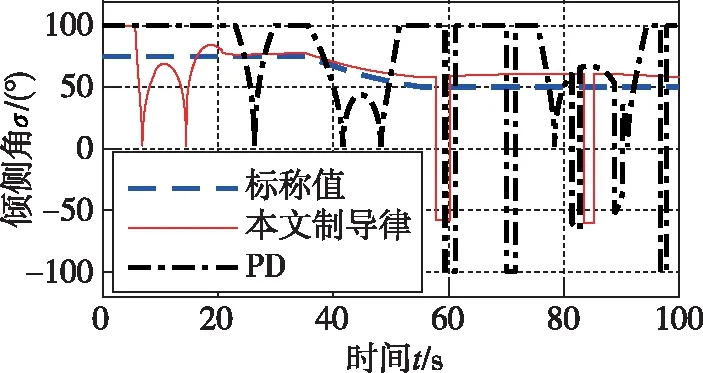
圖15 傾側角跟蹤曲線

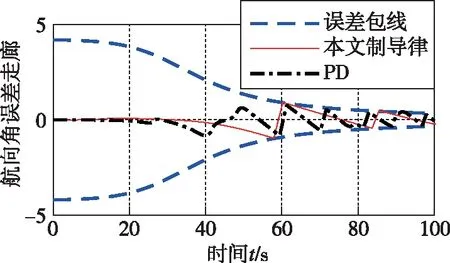
圖16 橫向漏斗走廊及航向角誤差

從圖1～圖4可以看出，在存在起始誤差的情況下，本文所設計的阻力加速度跟蹤制導律能夠實現快速、高精度的標稱阻力加速度跟蹤，最大跟蹤誤差為0.08872(m/s2)。而PD制導同樣能夠跟蹤上標稱的阻力加速度，但是過程中的跟蹤誤差要遠大于本文所設計的方法；從圖5～圖8、圖13可以看出，在縱向運動方向，本文所設計的制導律能夠保證火星探測器在大氣進入段對火心距r、速度V和飛行路徑角γ的跟蹤，火心距跟蹤的最大誤差為-1799m，速度的最大誤差為-55(m/s)，飛行路徑角的最大誤差為-3.745°，而PD制導的跟蹤誤差要遠大于本文所設計的制導律，這從側面說明了本文所設計的制導律的優越性。

從圖9～圖12、圖14可以看出，在橫向傾側角反號邏輯的作用下，針對縱向所設計的固定時間制導律依然滿足橫向運動要求，也證明了本文設計的橫向傾側角反號邏輯的正確性與可行性。在本文所設計的制導律的作用下，經度的最大誤差小于0.02°，緯度的最大誤差為-0.09°，航向角的最大誤差為±1°，且最大誤差發生在傾側角σ發生反號的時刻，精度均優于PD制導。從圖15和圖16可以看出，在航向角誤差到達航向角誤差漏斗走廊的邊界時，σ反號。在圖14相應時刻，航向角也向相反方向變化，使得航向角誤差減小。從圖14～圖16可知，在整個過程中，采用本文所設計的制導律的傾側角σ發生了4次反號，均未發生抖振現象，且航向誤差能夠控制在航向角誤差漏斗走廊。

為驗證所設計制導律的魯棒性，進行了100組蒙特卡羅仿真，仿真參數如表4所示，仿真結果如圖17～圖19所示。

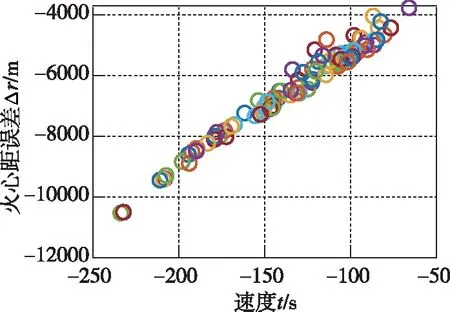
圖17 終端高度誤差與速度誤差分布

表4 蒙特卡羅仿真參數

從仿真結果可以看出，所設計的制導律及橫向反號邏輯在進入初始狀態具有較大偏差時仍具有很好的跟蹤效果，火心距的跟蹤誤差變化范圍為-10500m～-4000m，而且大部分火心距跟蹤誤差分布于-6000m～-4000m之間，經度變化范圍為-0.98°～-0.85°，大部分分布于-0.95°～-0.85°，緯度變化范圍為-0.42°～0°，大部分分布于-0.3°～0°。從圖19可以看出，對于不同的初始進入狀態，終端時刻的位置分布比較集中，且大部分分布在誤差較小的位置。

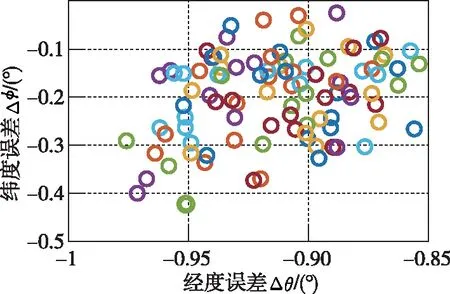
圖18 終端水平位置分布圖

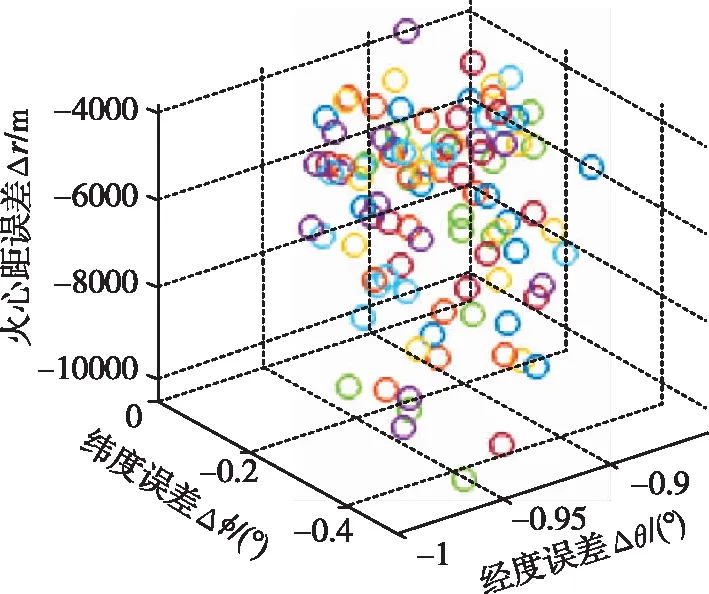
圖19 終端位置分布圖

4 結 論

本文研究了火星探測器大氣進入段的橫向運動和縱向運動的跟蹤制導律問題。針對橫向運動，給出了與速度呈線性關系的航向誤差漏斗走廊形式，設計了傾側角反號邏輯。通過合理選擇漏斗走廊參數，使得在起始階段跟蹤誤差較大時能避免傾側角頻繁反號，而在制導末端也能保證航向角跟蹤誤差收斂到較小的值，進而保證橫向運動的精度。與橫程漏斗走廊的傾側角反號邏輯相比，該邏輯計算簡單，可有效降低宇航計算機的運算壓力。與航向角誤差等寬走廊相比，該邏輯在高速時能夠有效避免傾側角的頻繁切換，提高任務成功概率。針對縱向運動，通過RBF神經網絡補償傾側角飽和問題，利用積分滑模設計了阻力加速度抗飽和固定時間跟蹤制導律，不僅避免了經典滑模控制固有的抖振問題，而且在制導律中引入的兩種不同形式的跟蹤誤差，一方面通過選取合理的參數有利于減小滑模控制帶來的抖振問題，另一方面還能保證在跟蹤誤差較大和較小兩種情況下均可加快收斂速度，保證跟蹤誤差在有限時間內收斂至0。通過數值仿真可以看出所設計的橫向傾側角反號邏輯和縱向制導律的有效性，且在初始狀態存在不確定性的情況下仍具有較高的跟蹤精度。