基于KPCA與KFDA的國六柴油機EGR系統故障診斷

王彥巖，馬騰飛，沈義濤，張正興，郝寶玉

(1.哈爾濱工業大學(威海)，山東 威海 264209;2.一汽解放商用車開發院，吉林 長春 130011)

廢氣再循環(EGR)技術是柴油機降低排放采取的重要技術手段之一，隨著國六排放標準進一步提高，系統的復雜性也大大增加，惡劣的工作環境更易使EGR系統出現故障，從而對排放性及經濟性帶來較大的影響。同時隨著柴油機的智能化，大量傳感器的使用使得信息融合技術應用更加廣泛，其通過對從多個信息源獲取的數據進行關聯和綜合來完成最終所需決策，可提高故障診斷的準確性。在此基礎上，基于數據驅動的故障診斷方法被廣泛應用，且目前正處于學術界和工業界全面重視的階段[1]。目前柴油機在線診斷是通過車載自診斷系統OBD(On Board Diagnostics)實現故障檢測，此方法對于電子類故障有較好的診斷效率和精度，但對機械故障的診斷精度低，機械故障更多依賴于線下人工診斷，已經無法滿足車主越來越高的需求[2-3]。SAE的IVHM(Integrated Vehicle Health Management)標準委員會定義了IVHM能力水平的進展，即從0級的基本“不自動化”到最終5級的“自適應健康管理”的目標[4]，而對數據的綜合處理在此過程起著至關重要的作用，也將是未來智能化發展的基石。

1 診斷方法及原理

主成分分析法(Principal Component Analysis, PCA)和Fisher判別分析法(FDA)都是基于數據驅動的多元統計方法，PCA是目前應用最廣泛的降維技術[5]，Fisher判別是一種常用的數據分類技術，已應用于許多工業過程的故障檢測和分類[6]，但在柴油機故障診斷方面以上兩種方法的使用并不多見。柴油機的結構及工作特性均十分復雜，EGR系統的過程變量眾多，各變量之間往往呈現出強耦合性和非線性[7]，無法根據變量變化直接獲得故障結果，故本研究在PCA和FDA的基礎上引入了核(Kernel)函數，組成了KPCA與KFDA相結合的多變量故障診斷方法。對于不同EGR故障下的過程數據，監測參數眾多，其數據的結構特點和分布特性具有差異性，從整個多元統計的角度來看，多變量的監測與分析弱化了部分數據之間的耦合性，這也是此類方法在大數據分析及機器學習領域的一個特點。

KPCA與KFDA相結合的柴油機EGR故障診斷方法原理見圖1。首先對數據進行采集，確定用于診斷的特征變量，然后提取出典型工況下各類故障的數據樣本，利用KPCA對高維數據樣本進行降維，再根據樣本故障類別定義數據標簽，將數據分為訓練集和測試集，分別用于訓練及測試KFDA分類器，最終通過KFDA分類器輸出測試集的數據標簽，確定故障類型，完成柴油機EGR系統故障的診斷。結果表明，與未使用核函數的線性方法(PCA+FDA)相比較，此方法具有更高的診斷精確度。

圖1 KPCA結合KFDA故障診斷原理

2 算法

2.1 核函數

核函數可增強對非線性數據的處理能力[8]，其主要思想是將原始輸入空間里的非線性數據映射到高維空間中，將非線性問題轉換為高維空間里的線性問題后再進行線性求解，思路見圖2，并且不同的核函數在處理不同的非線性數據時具有各自的效果及獨特的優點[9-10]。

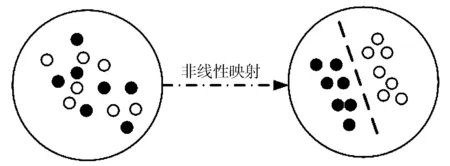
圖2 核函數映射示意

常見核函數有以下幾種：

線性核函數：

K(x,y)=xTy+c。

(1)

式中：c為常數。

多項式核函數：

K(x,y)=(axTy+c)d。

(2)

式中：c為常數；d為多項式階數。

高斯核函數：

(3)

式中：σ為函數的寬度參數,控制函數的徑向作用范圍。

2.2 KPCA

KPCA可以實現降維與提取非線性數據特征的雙重目標[10]。設原始數據集有n個樣本數，m個維度，經核方法將數據映射到高維空間后，計算其協方差矩陣，求得協方差矩陣的特征值λ及特征向量p，存在相關系數ai(i=1,2,…n)，使得

(4)

進一步簡化得

nλa=Ka。

(5)

式中：K為n×n的核矩陣;a為核矩陣K的特征向量。

Kjk=K(xj,xk)=φ(xj)Tφ(xk),

(6)

a=[a1,a2,…an]T。

(7)

通過求解核矩陣K，將特征值從大到小排列，以85%的累積方差貢獻率標準[11-12]，選取各特征值對應的特征向量組成特征空間的降維矩陣，新數據x在特征空間中為

(8)

2.3 KFDA

(9)

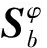
(10)

(11)

引入內積核函數替代特征空間里的內積計算：

K(xi,xj)=kij=φ(xi)φ(xj)。

(12)

wφ可以表示為

(13)

KFDA的目標可轉換為

(14)

其中：

(15)

(16)

ξx=[K(x1,x),…,K(xN,x)]T。

(17)

進行廣義特征值分析得到:

(18)

式中與特征值λ對應的特征向量a就是投影方向。求出投影方向后，確定分類的判別閾值yφ：

(19)

對于新數據x*的投影點y，若y>yφ，則新樣本屬于第0類；若y

3 故障監測及數據采集

對10輛搭載國六排放標準柴油機的車隊進行遠程在線監測，實時采集車輛運行狀態、ECU控制參數等共計100個參數，樣本采樣時間間隔為1 s，形成了車輛運行參數的大數據樣本集。試驗中單車行駛里程為5 000 km，監測中柴油機EGR系統出現了2個頻發故障，故障1為EGR冷卻效率低，故障2為EGR流量低，形成了一定數量的故障樣本。由于EGR率由新鮮進氣量與再循環廢氣量決定，又會受到溫度、壓力等的影響，故選擇進、排氣系統中的11個監測參數作為EGR故障診斷數據模型中的特征變量，分別為新鮮進氣量、總進氣量、進氣歧管壓力、進氣歧管溫度、排氣流量、渦前排溫、中冷后溫度、EGR溫度、EGR壓力值、EGR位置輸出值、EGR壓差輸出值。經過多次診斷試驗，結果證明能夠利用這11個變量實現對不同故障數據的有效識別，可以達到對故障進行診斷的需求。選取了柴油機運行中常出現的兩個典型工況(工況1：轉速為1 400±50 r/min，扭矩為2 200～2 400 N·m；工況2：轉速為1 200±50 r/min，扭矩為2 200～2 400 N·m)作為診斷工況。

4 故障診斷

EGR系統中選擇的11個特征變量與故障之間無線性對應關系，同時PCA是一種線性算法[15-16]，不能有效抽取出數據中的非線性結構特征[7]，而KPCA方法可以很好地解決此問題[17-18]，且它提供的特征數目更多、特征質量更高[19]，對于通過信息融合后的復雜數據源仍能夠有效完成數據降維。同理，針對非線性問題，KFDA可以更好地對非線性數據樣本進行處理[7-8,20-21]。經過使用不同核函數進行多次試驗，最終確定KPCA中的核函數使用線性核函數，KFDA中的核函數使用高斯核函數。

將圖1的診斷方法用于EGR系統故障診斷。故障診斷流程基于Matlab平臺，采集到數據后為避免噪聲干擾進行了去噪處理，然后通過Matlab軟件載入數據樣本，每個樣本均由11個過程變量的監測值組成；利用KPCA算法對數據實施降維，然后對正常狀態、EGR冷卻效率低、EGR流量低狀態下的三類數據定義類別標簽，分別為1、2、3，在此基礎上利用KFDA算法對訓練集數據訓練得到分類器；將測試集數據輸入分類器后，分類器根據判別閾值輸出每個數據對應的類別標簽，結果以莖狀圖的形式進行可視化，可根據莖狀圖里的類別標簽確定樣本數據對應的故障狀態，完成診斷。

選取工況1正常狀態、EGR冷卻效率低、EGR流量低狀態下的數據樣本各300個，對數據進行降維并標注類別標簽后按照3∶1的比例隨機分為訓練集和測試集，利用訓練集數據進行KFDA分類器訓練，最終分類器的訓練集精度達到99.41%。然后利用訓練好的分類器對測試集數據進行分類，測試集精度達到99.11%，結果見圖3。

圖3 工況1 KPCA+KFDA診斷結果

而PCA+FDA組合成的線性方法，對于柴油機參數中的非線性數據不能很好地進行判別，其訓練集精度為86.96%，測試集精度只有88%，結果見圖4。

圖4 工況1 PCA+FDA診斷結果

同理，選取工況2正常狀態、EGR冷卻效率低、EGR流量低狀態下的數據樣本，樣本數分別為161、187、183個，降維并標注類別標簽后按照3∶1的比例隨機分為訓練集和測試集，利用訓練集數據進行KFDA分類器訓練，最終訓練集精度達到95.98%。然后利用分類器對測試集數據進行分類，測試集精度達到了90.98%，受到工況及樣本數量的影響，其精確度略低于工況1，結果見圖5。而PCA+FDA組合成的線性方法，其訓練集精度為82.41%，測試集精度為87.97%，結果見圖6。

圖5 工況2 KPCA+KFDA診斷結果

圖6 工況2 PCA+FDA診斷結

由診斷結果可知，在原有線性方法的基礎上結合核函數，可以有效處理EGR系統中的非線性過程變量，進一步提高故障的診斷精確度，并能夠較為準確地診斷出EGR系統的冷卻效率低故障和流量低故障。

5 結束語

針對柴油機EGR系統的非線性問題，引入了核方法，可提高對EGR系統非線性問題的處理能力。提出基于KPCA與KFDA結合的柴油機EGR系統故障診斷方法，對EGR冷卻效率低和EGR流量低兩類故障多次驗證后，診斷精度最高達到99.11%。將此方法向柴油機其他系統拓展，對于建立柴油機整機在線健康管理系統，提高柴油機運行可靠性，具有重要意義。