混合動力汽車工況識別及動態協調策略研究
吳靜波,李明明,盧耀真,郭志軍
(1.河南省汽車節能與新能源重點實驗室,河南 洛陽 471000;2.河南科技大學車輛與交通工程學院,河南 洛陽 471000)
與傳統燃油車相比,混合動力汽車擁有多種運行模式,如何合理地進行切換,實現節能減排,能量管理策略的制定是關鍵,而行駛工況是能量管理策略制定的基礎,若能依據當前行駛工況的特點合理分配各個動力源的扭矩,可以進一步改善車輛的燃油經濟性[1]。但是,車輛在道路上行駛時,實際工況是復雜多變的,因此,行駛工況的在線識別對能量管理策略的開發具有重大意義。
近些年,一些國內外學者在研究行駛工況的預測和判別時,主要采用模型預測的控制方法,預測汽車在未來時域內的扭矩需求,實時優化變量并得到扭矩分配比等參數。Borhan等[2]指出,混合動力汽車的需求扭矩在未來時域內將會按照指數函數的形式衰減,提出建立線性優化控制模型,然而,指數函數在預測車輛的動力需求時存在著很大的誤差。Zhang等[3]建立了神經網絡模型對駕駛員行為進行在線分類,并將駕駛員行為和預測的交通信息整合在一起優化目標函數,但是這些都需要大量的數據對神經網絡進行訓練,而且存在收斂速度慢等缺點。劉爽等[4]提出了一種基于駕駛意圖識別的NAR神經網絡短期工況預測方法,將模糊推理得到的駕駛意圖與歷史車速數據共同用于NAR神經網絡短期工況預測。秦大同等[5]在應用歐幾里得貼近度識別工況的基礎上,運用粒子群算法優化不同工況下的汽車能量管理控制參數,但是常規的粒子群算法易陷入局部極值而出現早熟收斂,往往達不到全局最優。上述這些方法在進行工況預測時均未考慮在工況發生突變時產生的動態油耗等問題。
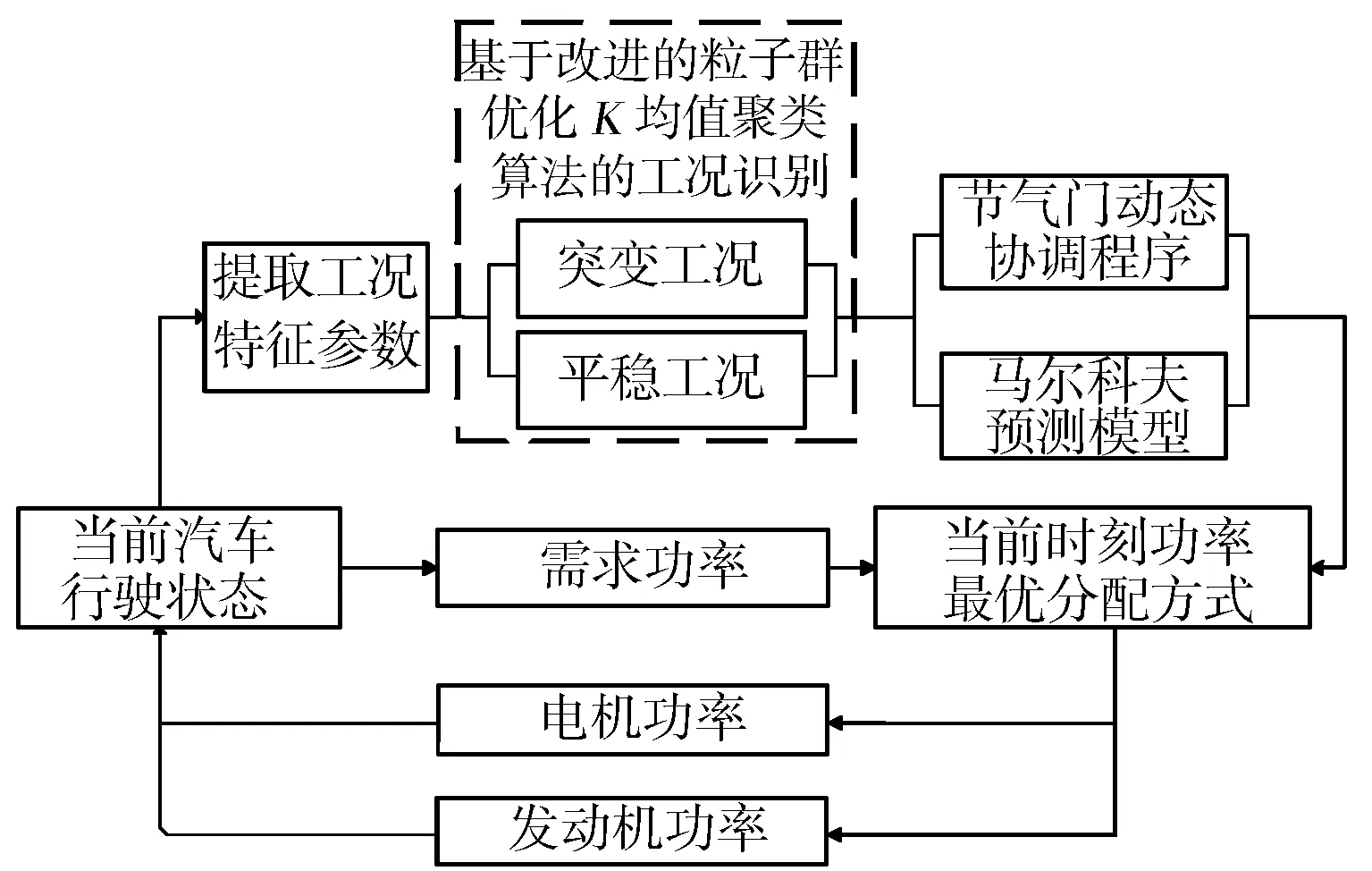
針對以上存在的問題,本研究在常規的粒子群算法基礎之上進行改進,利用改進后的粒子群算法優化K均值聚類中心,之后進行工況分類[6]。針對不同的工況類型采用馬爾科夫鏈或限制節氣門開度變化率的方法對需求扭矩進行合理分配,并建立優化目標函數和約束條件,通過優化算法進行求解得到最優控制變量,從而降低混合動力汽車在工況突變時產生的動態油耗,改善行駛平順性。
1 并聯式混合動力系統模型
1.1 系統結構
本研究以BSG型混合動力汽車為研究對象,主要部件包括BSG(帶傳動一體化起動/發電機)、發動機、CVT變速器、動力電池等。BSG電機取代了傳統的起動機,當其作為電動機時,動力電池放電提供助力;當其作為發電機時,動力電池處于充電狀態,而且在啟動時加入了電池自加熱的功能,克服了在極端天氣下啟動困難等問題。系統結構見圖1,整車主要部件參數見表1。
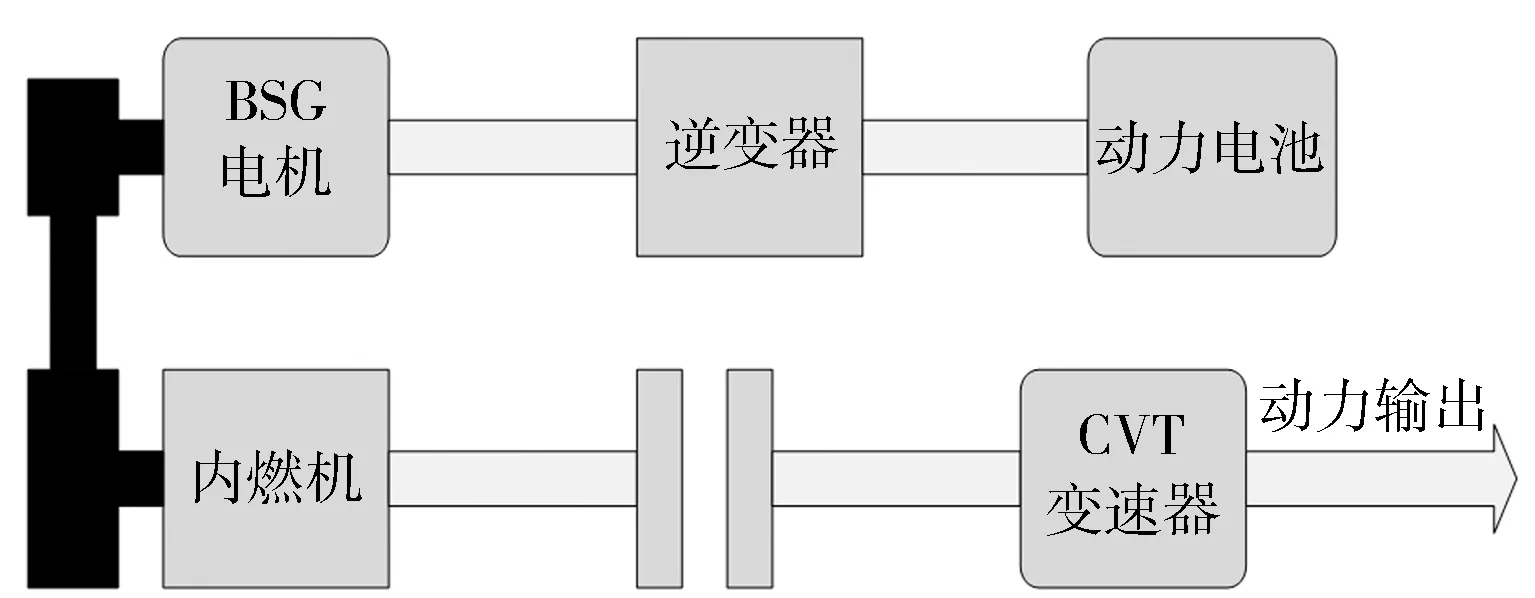
圖1 BSG混合動力系統結構示意
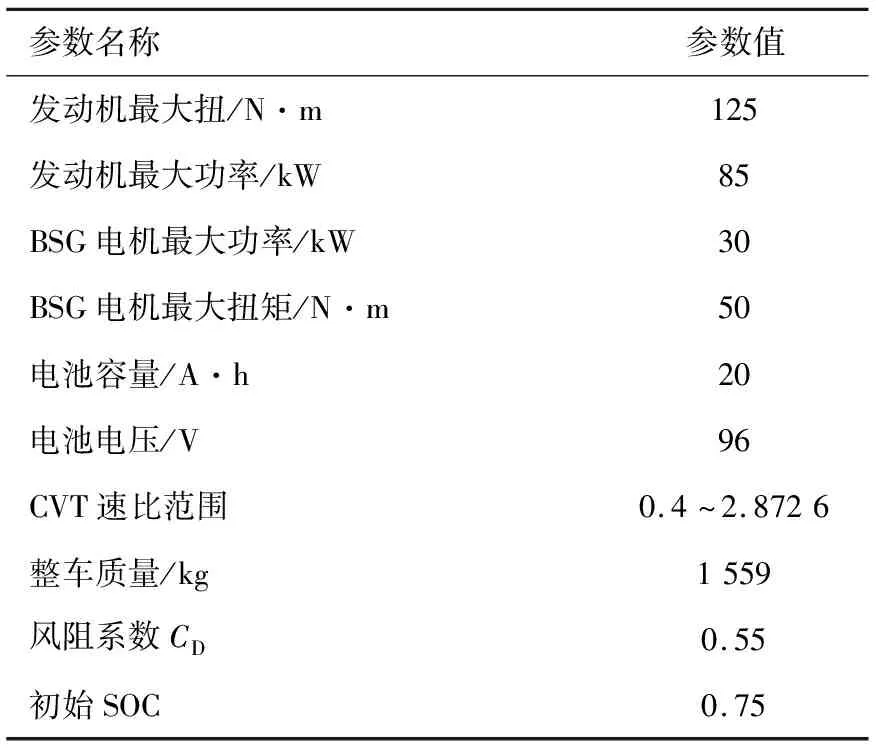
表1 整車主要部件參數
1.2 混合動力汽車動力學模型
動力學模型為
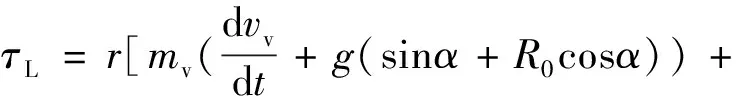
0.5ρairCdAfvv2],
(1)
ωL=vv/r,
(2)
ωe=ωLi0h,
(3)
(4)
式中:τL為車輪需求扭矩;vv為行駛速度;ρair為空氣密度;R0為滾動阻力系數;α為坡度角;Cd為空氣阻力系數;Af為迎風面積;mv為整車質量;g為重力加速度;ωL為車輪轉速;r為車輪半徑;h為換擋速比;ωe為發動機轉速;τe為發動機扭矩;ηf為傳動系統效率。
電機特性可描述為
Tm_min=fm_min(ωm),
(5)
Tm_max=fm_max(ωm),
(6)
Tm∈[Tm_min,Tm_max],
(7)
ηm=fm_map(Tm,ωm),
(8)
(9)
Ib=Pb/Vb。
(10)
式中:Tm_min,Tm_max分別為電機最小、最大扭矩;fm_min(ωm)為電機制動扭矩特性查表函數;fm_max(ωm)為電機驅動扭矩特性查表函數;ηm為電機效率;fm_map為電機效率函數;Ib為動力電池輸出電流;Pb為輸出功率;Vb為端電壓。電機效率見圖2。

圖2 電機效率Map圖
2 工況在線識別
2.1 典型循環工況的構建
利用K均值聚類算法在離線狀態下對工況進行劃分,依據工況內的車速波動和節氣門開度變化率,將行駛工況劃分為平緩工況和突變工況。為了正確識別行駛工況的類型,需要謹慎提取工況特征參數。在綜合考慮其他學者選擇特征參數的基礎之上,按照特征參數對工況識別的重要性,本研究選擇了7個參數作為工況識別的特征參數[7],分別為最高車速vmax、最低車速vmin、車速標準差vavg、最大加速度amax、最大減速度dmax、加速時間t、加速度標準方差ad。圖3示出選取Cruise中25種工況構成的識別樣本。
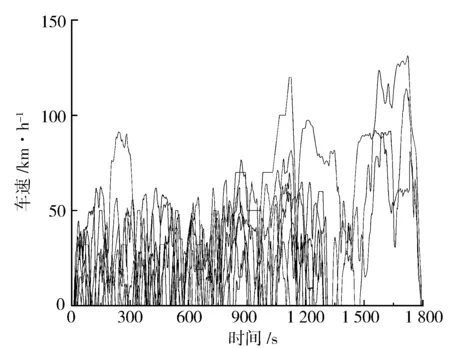
圖3 綜合后的基礎工況
2.2 行駛工況的聚類
2.2.1改進粒子群優化K均值初始聚類中心
K均值算法的聚類中心選取時比較敏感,存在容易陷入局部最優解的缺陷。本研究將粒子群算法(PSO)與K均值聚類算法相結合,運用PSO算法的全局搜索能力對K-means算法的初始聚類中心進行優化,PSO算法具有在解空間中搜索的隨機性特點,可以大大減小K-means算法陷入局部極值的概率,提高聚類結果的準確率[8]。
常規的PSO算法易陷入局部極值而出現早熟收斂的現象,因此本研究對各個粒子以及粒子群的最優值進行實時優化,對因陷入局部極值而出現早熟收斂的粒子進行變異,增加粒子群的多樣性[9],并采取以下公式更新粒子狀態:
vid(t+1)=ωvid(t)+c1r1(pi-xid)+
c2r2(pg-xid),
(11)
xid(t+1)=xid(t)+vid(t+1),
i=1,2,…n;d=1,2,…D。
(12)
式中:vid(t),xid(t)為第t次迭代時粒子i的速度和位置;pi,pg為粒子i的個體最優位置和群體最優位置;ω為慣性權重系數;c1,c2為學習因子;r1,r2為隨機權重。
pi可通過以下公式進行更新:
pi(t+1)=
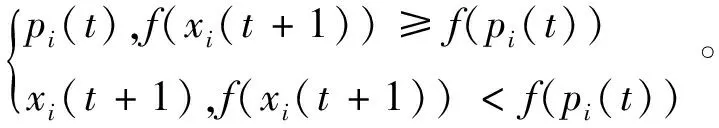
(13)
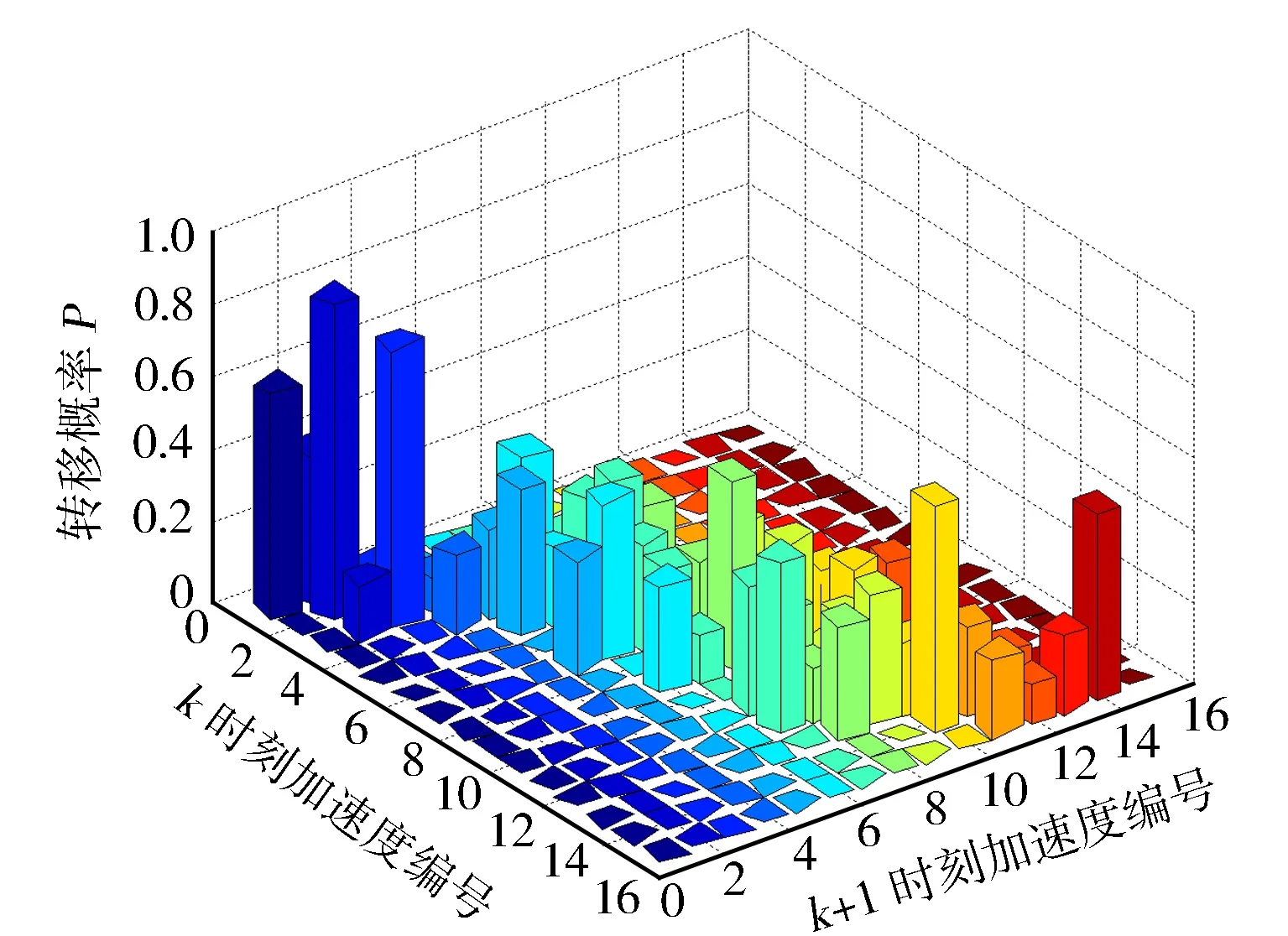
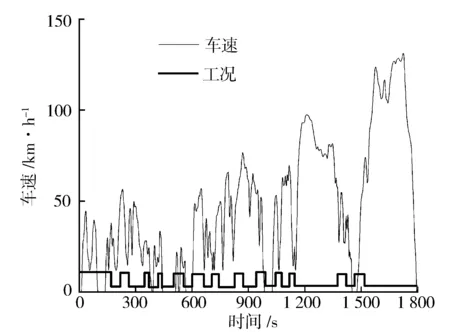
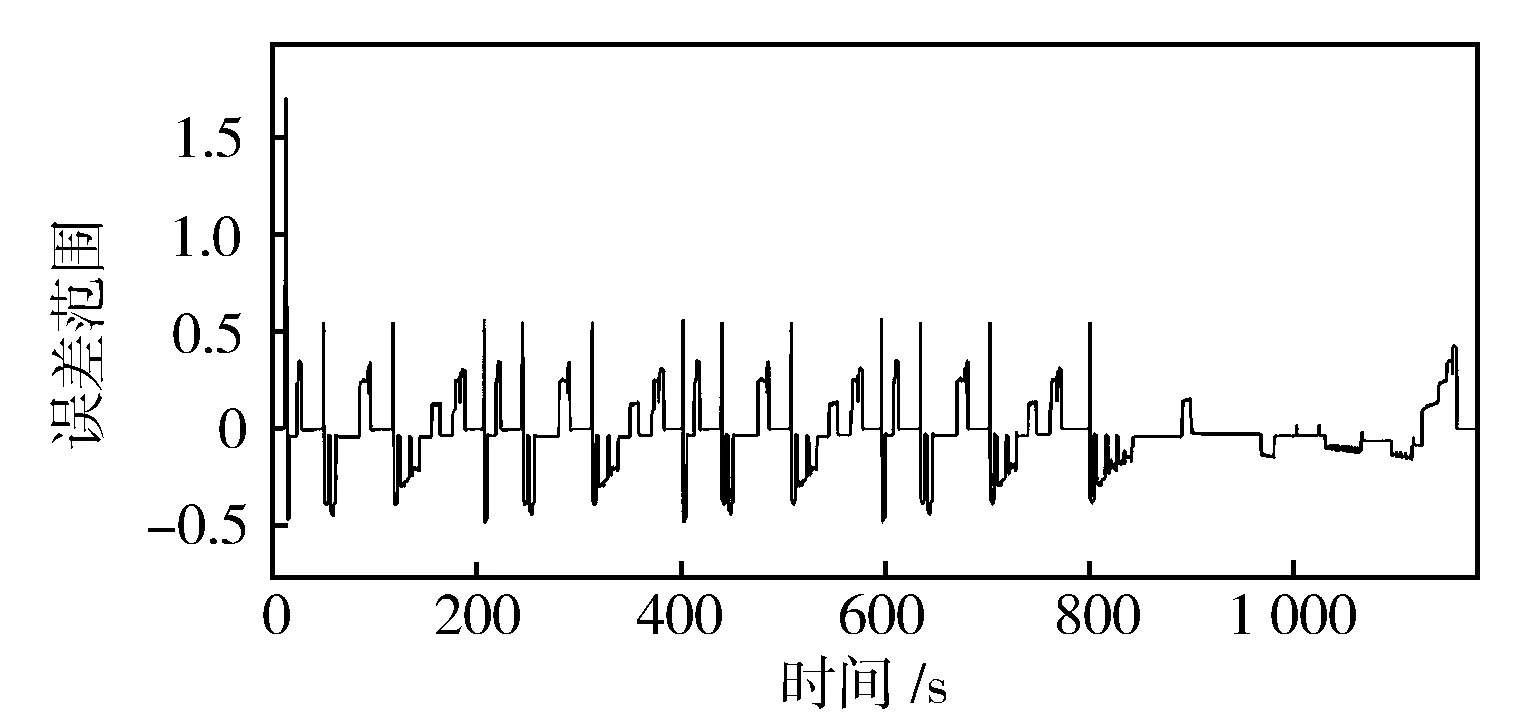
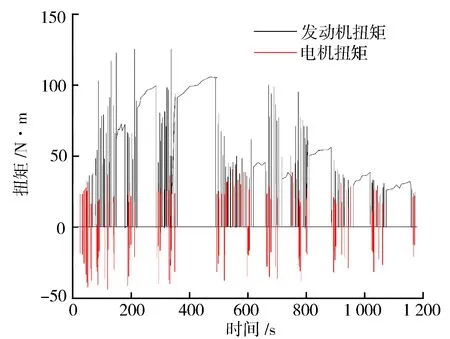
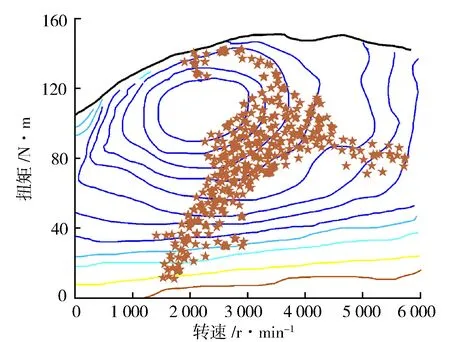
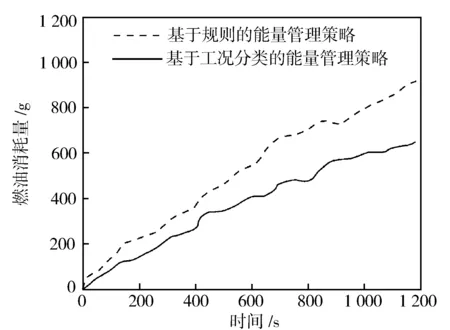
式中:f(x)為粒子群的適應度函數;f(xi(t+1)) 2.2.2離線劃分和在線識別 離線劃分: 1)本研究進行工況判別的周期為120 s,判別結果每5 s更新一次,提取典型循環工況中每一采樣時刻過去10 s的工況特征參數,將提取的特征參數作為一個數組[10],得到樣本數組[x11,x12,…x1m],[x21,x22,…x2m],…[xn1,xn2,…xnm],其中m為特征參數數目,n為循環工況長度。 2)利用改進后的粒子群算法優化K均值算法的初始聚類中心,對待識別的工況數據進行聚類劃分,得到最終的聚類中心c1=[c11,c12,…c1m],c2=[c21,c22,…c2m],計算識別周期內待識別的工況數據到聚類中心的歐氏距離,并將數據按照就近原則分配到鄰近的簇內。 3)根據聚類后得到的工況數據,計算聚類c1、聚類c2的類內差異w(C)、類間差異b(C)和準則函數E。 K均值算法的準則函數E為 (14) 類內差異w(C)為 (15) 類間差異b(C)為 (16) 不斷調整聚類中心,直到準則函數E、w(C)、b(C)不再發生變動,則認為分類穩定,最終得到平緩工況的聚類中心c1和突變工況的聚類中心c2。 在線識別: 1)在混合動力汽車行駛過程中提取識別周期內隨機工況的特征參數。 2)將提取的特征參數看作一個數組,根據下式計算該數組與各個最終聚類中心的歐氏距離。 (17) 3)將距離聚類中心c1或c2最近的一組工況數據視為該工況所屬的簇,此簇中當前時刻的工況為該簇所代表的工況類型[9]。 平緩工況下,若能預知混合動力汽車在未來時域內的駕駛狀態,便可以在當前時刻運用算法優化車輛在該時域內的駕駛狀態。車輛的加速度在任一時刻只由當前的狀態所決定,而與過去的狀態無關,可認為車輛加速度的變化是一種馬爾科夫過程,即在行駛過程中把車輛的加速度當作預測量,加速度的未來狀態視為一種概率分布,而概率分布可以從過去的行車數據或標準工況中提取和歸納。計算當前時刻加速度概率向下一時刻轉移的關鍵是計算出概率轉移矩陣,其中,概率轉移矩陣中的每一個元素分別代表了加速度從當前時刻向下一時刻轉移的概率[11],選取轉移矩陣中概率最大值作為確定下一時刻的加速度值。 混合動力汽車行駛屬于時間連續、狀態離散的過程,令an為加速度的集合,可離散為有限的數值: an∈{a1,a2,a3,…am}。 (18) 預測加速度的變化即是描述轉移概率矩陣P(a,b)。 令向量 P(k+i)=(Pq1(k+i),Pq2(k+i), Pq3(k+i),…Pqs(k+i))。 (19) 式中:Pqs(k+i)表示在t(k+i)時刻加速度大小在qs處的概率。因此可以得出以下關系式: P(k+n-1)=P(k+n-2)PM= P(k)(PM)n-1。 (20) 若在t(k)時刻,加速度大小τ(k)已知,所以P(k)已知,根據上式求出加速度在預測時域內各個預測點處的位置分布概率。 Pa,b的值能通過最大似然預測法確定: (21) (22) a,b∈{1,2,…S}。 (23) 式中:M(a,b)為加速度從a轉移到b的次數;Ma為加速度從a轉移的次數之和。 將新歐洲行駛工況(NEDC)、城市道路循環工況(UDDS)、中國城市工況(CUDS)和全球統一輕型車測試規程(WLTP)4種工況作為樣本工況來提取車速及加速度數據,得到了轉移概率矩陣。圖4示出由k時刻的加速度向(k+1)時刻轉移的概率分布。 圖4 馬爾科夫鏈模型轉移概率分布 根據建立的馬爾科夫模型,可由當前k時刻的加速度預測出(k+1)時刻的加速度,并求出(k+1)時刻車速: (24) 基于(k+1)時刻車速,在預測周期內不斷更新預測區間,采用動態規劃算法得到發動機和電機扭矩輸出[12],實現最優的扭矩分配,設第t0階段預測時域th時刻優化目標函數為 ωv(v(t+1)-vtar(t+1)2)]dt。 (25) 式中:ωm,ωs,ωv為權重系數,SOCr為SOC參考值,vtar為預測車速。 同時對SOC進行約束,其表達式為 (26) 式中:α為常數,計算過程中取值105。 經過上述分析,綜合考慮研究對象的運動特性,馬爾科夫模型預測方法在平緩工況下能有效預測未來車速,根據設定的目標函數進行扭矩最優分配,但在突變工況下此方法無效。因此,針對突變工況,本研究采用PID控制算法限制節氣門開度變化率和電動機補償差值扭矩的方法,有效地避免了燃油過度噴射和混合動力汽車模式切換過程中造成的沖擊[13]。 通過PID控制算法限制節氣門開度變化率,在突變工況下,整車控制器VCU對需求扭矩進行分配,當發動機控制器ECU接收到目標扭矩之后,對目標扭矩進行解析,將其解析成節氣門開度β的指令。節氣門開度變化率在單位時間內的增量是一個有限的數值,根據積分性質可知,若對未來一段預測區間內的節氣門開度變化率Δβ進行積分,可得到具體的節氣門開度數值。將節氣門開度變化率Δβ作為PID控制器的輸出,實現對發動機輸出扭矩的控制,可表示為 |Δβ|=min{|Δα|,|kp·e+ (27) 燃油流量可以從具體的燃油效率Map圖中通過下式計算: (28) 式中:e=Te_tar-Te_act為發動機扭矩偏差控制量;Te_tar,Te_act分別為發動機的目標扭矩和實際扭矩;kp,ki,kd分別為比例、積分、微分增益系數;|Δβmax|為限制的最大節氣門開度變化率。發動機的扭矩控制見圖5。 圖5 發動機的扭矩控制圖 利用電機響應迅速的優點來補償節氣門動態協調控制中的差值,電機的目標扭矩為 Tm_tar=Treq-Te。 (29) 電機在輸出扭矩時會受到自身的一些限制,因此對電機進行約束: (30) 式中:Tm為電機輸出扭矩;Treq為整車需求扭矩;Tm_max為電機的最大輸出扭矩。 節氣門開度調節過程中,發動機的輸出扭矩為Te: (31) 式中:Te_tar為發動機目標扭矩;Δβ為發動機節氣門開度變化率;Δβlimit為發動機節氣門開度變化率的限制值。 當發動機節氣門的開度變化率大于Δβlimit時,對發動機進行動態協調控制,限制節氣門的開度變化率在|Δβ|內,利用電機的快速響應特性來補償減少的扭矩差值,同時保證兩者的扭矩之和不會發生大的波動[14],避免節氣門突變時燃油經濟性和排放的惡化。限制后的發動機和電動機動態扭矩控制結構見圖6。 圖6 限制后的發動機和電動機動態扭矩控制結構 在Matlab/Simulink中搭建整車仿真模型,驗證該策略的合理性。仿真過程中把能量管理控制策略的采樣時間間隔設置為0.5 s[15],同時設定預測時域P=6 s,電池SOC初始值為0.75,參考值為0.55。圖7示出改進粒子群優化K均值聚類算法的工況分類動態協調控制策略示意。 圖7 改進粒子群優化K均值聚類算法的工況分類動態協調控制策略示意 圖8示出工況在線分類的仿真過程,在構建的循環工況中隨機提取一段典型工況進行判別。由圖8可知:車速加劇變化時,如在245—460 s,670—750 s和960—1 120 s,工況可判別為突變工況;而當車速在小范疇內波動或車速緩慢加減速時,如760—970 s,1 160—1 335 s和1 510—1 760 s,工況判別為平緩工況。由此可見,對工況進行分類的方法是有效的。 圖8 在線工況判別結果 圖9示出車速預測結果。由圖9可知,通過對工況的在線分類和識別之后,能夠較為準確地預測出該工況下的行駛車速。 圖9 車速預測結果 為了更準確地評估預測值與真實值之間的誤差,引入平均絕對誤差MAE(Mean Absolute Error)作為評價指標。MAE表示預測值與真實值絕對誤差的平均值,能更好地反映兩者誤差的實際情況,計算公式如下: (32) (33) 式中:MAE(k)為綜合循環工況中第k個采樣點在下一時域內的平均絕對誤差;MAE為整個綜合循環工況下的平均絕對誤差;NC為綜合循環工況下的采樣點個數;va(k+i)為綜合循環工況下第(k+i)個真實車速的采樣點,誤差范圍0~0.5。圖10示出預測車速和實際車速之間誤差。 圖10 預測車速與實際車速之間的誤差 由圖11仿真結果可知,針對綜合循環工況,采用限制節氣門開度變化率的動態協調控制策略后,車速和電機轉速的波動僅為0.1 m/s和20 r/min。仿真結果表明,如110—190 s時間段加速度發生突變,經過動態協調控制策略控制之后,由油門突變引起的對傳動系統的沖擊明顯減小,提高了模式切換時的行駛平順性。 圖11 動態協調仿真結果 建立動態協調控制策略的仿真模型,與傳統的混合動力汽車進行對比分析,圖12示出綜合循環工況下發動機與電機的輸出扭矩,圖13和圖14示出分類前后發動機的工作點分布。由圖可以看出,采用該策略之后,車輛能夠依據不同的工況合理地分配需求扭矩,在平緩工況下,發動機承擔了幾乎所有需求扭矩,并在高效率區運行;突變工況下,通過控制節氣門的開度變化率,車輛更好地協調了BSG電機和發動機之間的扭矩分配,由于節氣門開度變化更平緩,所以發動機也能夠更好地維持在高效率區工作。 圖12 發動機和電機的輸出扭矩 圖13 工況分類前發動機工作點 圖14 工況分類后發動機工作點 從圖15可以看出,經過工況劃分后,車輛在保證了動力性的基礎上,有效改善了燃油經濟性。 圖15 不同能量管理策略的燃油消耗曲線 本研究中,選取識別時間P=6 s,在WLTP工況下,與未采用工況分類的控制策略進行對比,對采用工況分類的控制模型編寫m程序,并通過仿真模型調用程序。從圖16至圖18的仿真結果可以看出,驅動電機大多工作在25~55 N·m之間的高效區域,工作效率在89%以上,能有效提高系統的工作效率。 圖16 綜合測試工況電機工作點分布 圖17 綜合測試工況下電機扭矩 圖18 綜合測試工況下電機效率 圖19示出電池SOC的仿真結果。工況的在線分類屬于一種實時優化,能夠合理地通過電池SOC的波動來調節發動機,保證發動機在高效區工作,并且電池SOC值變化平穩,保持在高效區0.5~0.7之間波動,既可以保證電池高效充放電,又可避免汽車在運行過程中由于動力電池SOC下降過快電機無法實現扭矩補償的功能。本研究在保證了汽車的動力性與經濟性的情形下,驗證了動態協調控制策略的合理性。 圖19 不同策略下電池SOC仿真結果 表2列出基于工況在線分類的能量管理控制策略。與未采取工況分類的能量管理控制策略的仿真對比,對節氣門的開度變化率進行了限制,表中Q100表示綜合測試工況下折合成的百公里油耗。與常規的混合動力汽車相比,采用本研究提出的基于工況分類的動態協調控制策略后,在整個綜合測試工況下燃油消耗降低10.88%,表明該控制策略能夠通過行駛工況的不同,合理地改善車輛在工作模式切換時帶來的沖擊,降低整車的綜合燃油消耗。 表2 燃油經濟性對比 混合動力汽車不同的行駛工況對能量管理策略控制效果的影響也不相同,因此,本研究提出了行駛工況在線分類判別的方法,將行駛工況分為平緩工況和突變工況,分類結果可為實現混合動力汽車動態扭矩協調控制提供理論基礎。 平緩工況下利用馬爾科夫模型進行車速預測,突變工況下對發動機節氣門的開度變化率進行限制,大大減少了由于油門突變帶來的動態油耗以及對傳動系統造成的沖擊,在改善了燃油經濟性的同時,提高了行駛平順性。 基于Matlab/Simulink仿真軟件,建立整車控制策略仿真模型,驗證了所提出的改進粒子群優化K均值算法進行工況分類的動態協調控制策略的合理性。結果表明,該策略可使汽車在行駛過程中,大大減小在突變工況下產生的動態油耗,同時電池的SOC下降速度明顯降低,有效防止了汽車在運行過程中由于電池SOC下降過快,電機無法提供助力的問題。
2.3 平緩工況下的扭矩分配
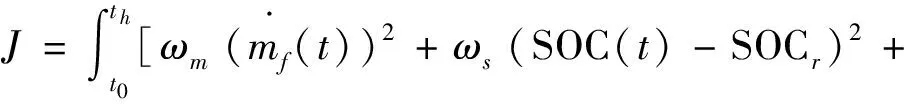
2.4 突變工況下的動態協調
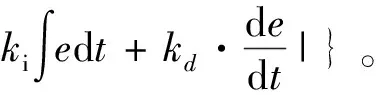
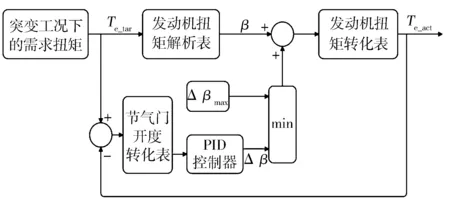
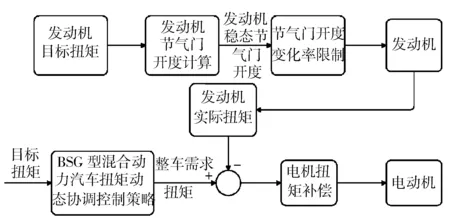
3 仿真結果與分析








4 結束語

