構建數學模型 挖掘思維深度

高買花 徐甜甜

【摘?要】對最短路徑問題的研究，可利用思維轉換，將一個實際問題通過建立數學模型的方式，“轉化”成數學幾何問題;再結合相應的數學定理，進行合情推理、邏輯證明，解決這個數學問題;最后再將得到的結論“還原”至實際問題之中。在此實證過程中，教師作為引導者，需要給予學生及時、合理的指引，讓學生通過不斷的思考和練習，提升邏輯思維能力、推理論證能力和歸納總結能力。

【關鍵詞】最短路徑;化歸;創新提高

古往今來，最短路徑問題都是人們不斷探索研究的經典問題，李頎的《古從軍行》中“白日登山望烽火，黃昏飲馬傍交河”就體現了這一問題。作為一名數學教師，筆者認為對最短路徑問題的研究，可利用思維轉換，將一個實際問題，通過建立數學模型的方式，“轉化”成數學幾何問題;再結合相應的數學定理，進行合情推理、邏輯證明，解決這個數學問題;最后再將得到的結論“還原”至實際問題之中。在此實證過程中，教師作為引導者，需要給予學生及時、合理的指引，讓學生通過不斷的思考和練習，提升邏輯思維能力、推理論證能力和歸納總結能力。本文將通過詳細分析講解數學教學中出現的最短路徑問題，進行相應數學建模的探索。

一、聯系“化歸”思想，建立歸納模型

“化歸”即轉化歸納，由難化易，由繁化簡。在中學數學的學習中，化歸思想無處不在，在解決主要考查內容一致但形式多變的數學問題時，我們需要運用化歸思想，將復雜多變的問題轉化成熟悉一致的問題。通過多次練習熟悉了這些相似的數學問題之后，便可建立模型，進行歸納總結。

例如：

古希臘亞地山大里亞城有一位久負盛名的學者，名叫海倫。有一天，有位將軍不遠萬里專程前來向海倫求教一個百思不得其解的問題：將軍從營地回家，需橫跨一條河流，請問在哪兒過河路徑最短？（不考慮河流的寬度）

模型一：兩點在同一直線異側

請問：將軍從營地回家，從哪里過河路程最短？理論依據是什么？

模型二：兩點在一直線同側?（著名的“將軍飲馬”問題）

請問：將軍和營地在河流同側，戰馬在回家途中渴了，問：將軍在哪里飲馬路程最短？

模型三：“兩線一點”型的線段和的最小值問題

某中學舉行文藝晚會，桌子擺成兩直排（AO、BO相較于點O），AO桌面上擺滿了橘子，BO桌面上擺滿了糖果，站在P處的學生小明先拿橘子再拿糖果，然后到P處座位就坐，請你幫他設計一條行走路線，使其所走的總路程最短。

模型四：“兩點兩線”型的線段和的最小值問題

有兩條街道AO、BO相交于點O，街道AO賣水果，街道BO賣文具，同學C和同學D分別在街道前面的草坪上做游戲，同學C先去街道AO買水果，再去街道BO買文具，送給同學D，請問，同學C怎么走路程最短？

以上四個模型，均以生活實際問題為背景，需要我們將實際問題中的圖形和數據進行處理，將此生活問題轉化為幾何問題，如“河流”“桌子”“街道”可以類比為直線、射線，或者線段，“人”可以類比為“點”，將情境中的物體具體化為幾何圖形以后，便可根據其特點，結合相應的知識或定理，進行模型的分類、歸納。

學會建立數學模型，可以幫助學生從千變萬化的題目之中，找到題目的共性，運用“化歸”思想，將不同的數學題目整理為相同的數學模型，提高學生的做題效率，逐步形成由繁化簡的數學思維。

二、層層遞進，提升建模能力

在學會基礎的建模以后，學生對怎樣建立數學模型已經有了相應的了解，在此基礎之上，我們可以通過對題目類型和難度的篩選，設置相應的梯度，層層遞進，提升學生的思維能力和建模能力。

模型一：題中出現一個動點

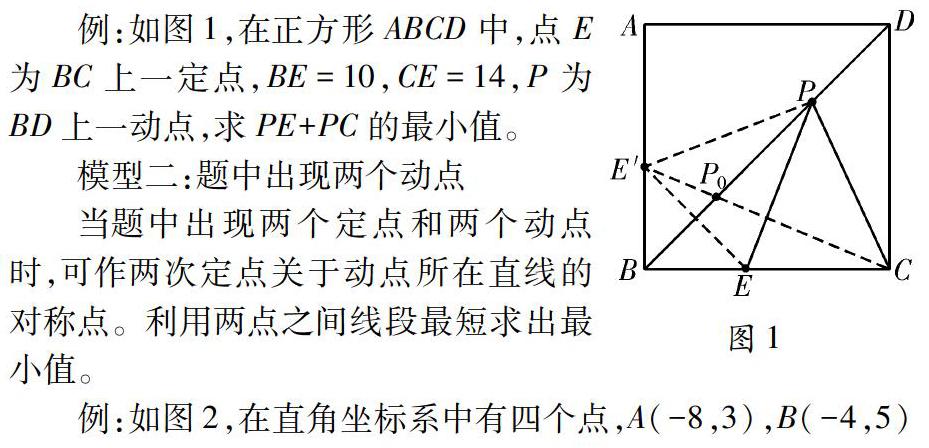
當題中只出現一個動點時，可作定點關于動點所在直線的對稱點，利用兩點之間線段最短，或三角形兩邊之和大于第三邊求出最小值。

例：如圖1，在正方形ABCD中，點E為BC上一定點，BE=10，CE=14，P為BD上一動點，求PE+PC的最小值。

模型二：題中出現兩個動點

當題中出現兩個定點和兩個動點時，可作兩次定點關于動點所在直線的對稱點。利用兩點之間線段最短求出最小值。

例：如圖2，在直角坐標系中有四個點，A（-8，3），B（-4，5）C（0，n），D（m，0），當四邊形ABCD周長最短時，求mn。

模型三：題中出現三個動點時

（1）作定點關于動點所在直線的對稱點;

（2）同時要考慮點點、點線、線線之間的最短問題。

例：如圖3，在菱形ABCD中，AB=2，∠BAD=60°，E，F，P分別為AB，BC，AC上的動點，求PE+PF的最小值。

三、創新提高，融匯建模思想

在數學教學中，教師除了向學生傳授知識，并幫助他們學會歸納知識以外，更重要的是培養學生的創新思維和進取提高意識。我們可以通過一些新穎有趣的數學題，激發學生的思考探索意識，并從中獲得突破自我的解題體驗。在此過程中，學生不僅可以提升自己的思維能力，還能強化建模意識。

模型一：立體幾何中的最短路徑問題

桌上有一個圓柱形玻璃杯（無蓋），高為12厘米，底面周長18厘米，在杯口內壁離杯口3厘米的A處有一滴蜜糖，一只小蟲從桌上爬至杯子外壁，當它正好爬至蜜糖相對方向離桌面3厘米的B處時，突然發現了蜜糖，問小蟲至少爬多少厘米才能到達蜜糖所在位置？

把圓柱展開，得到一個矩形，作點A關于矩形邊長的對稱點，最短距離就是線段的長，根據勾股定理解答即可。

模型二：二次函數中的最短路徑問題

點D是拋物線y=-14x2+12x+154的頂點，點E在拋物線上，橫坐標為4。M、N分別為?x軸、y軸上的動點，順次連接D、N、M、E構成四邊形DNME，求四邊形DNME周長最小時點M和點N的坐標。

將最短路徑問題和函數聯系在一起，使得求兩條線段之和轉化為求三條線段之和，有助于培養學生的類比能力和創新能力。

四、結語

在初中數學的學習中，題目形式是多變的，但知識點和方法是相對固定的。在實際教學過程中，教師應有意識地幫助學生學會準確地在海量的題目之中分析出題目要考查的知識點，歸納相應的題目類型并建立正確的數學模型，運用“化歸”思想，將題目清晰化、簡單化;做到對從“題目由繁化簡”到“快速準確建立數學模型”這一過程中學生可能出現的知識誤區和盲點及時梳理，從而使學生能“由簡入繁”地掌握“由繁到簡”的學習方法，培養學生思維的廣闊性、敏捷性、靈活性，實現“量”到“質”的飛躍，讓不同學習能力的學生在不同的學習階段都能學有所悟、學有所樂。

參考文獻：

[1]王小莉.化歸思想在中學數學教學中的滲透[J].教育現代化，2018（10）.

[2]魏玉琴.“最短路徑”問題中化歸思想的應用與策略[A].2019年中小學學素質創新研究大會，2019.

[3]尹加根.解析初中數學教學中的最短路徑問題[J].數學學習與研究，2018（17）.

[4]張媛.關于初中數學最短路徑問題的探究[J].高考，2017（06）.

[5]蘆英峰.初中數學最短路徑問題的探究與延伸[J].學苑教育，2016（10）.