基于行波法的段塞流瞬態捕捉模型建立與驗證

王冬旭，胡其會，李玉星，李爽，王權

（1 中國石油大學（華東），山東省油氣儲運安全省級重點實驗室，山東青島266580；2 中國市政工程中南設計研究總院有限公司，湖北武漢430060）

段塞流是油氣混輸管線中的常見流型，當管線處于啟動、停輸、清管、輸量變化甚至正常生產時，都有可能產生[1]。其流動的間歇性將引起管道中持液率和壓力的急劇波動，并使得下游管道及設備承受間歇性應力沖擊[2-4]。同時，管道末端產生的大段塞會引起下游處理設備中液位劇烈波動。為保證管線和下游處理設備的安全生產，必須掌握段塞流的特征規律。為此，自20 世紀40 年代起，國內外學者對段塞流開展了相關研究[5-7]。

Dukler 等[8]最早建立了氣泡和段塞在時間和空間內呈均勻分布的段塞流穩態模型。此模型可以預測段塞流重要參數的平均值，如段塞長度、氣泡平移速度和壓降。Ishii[9]在20世紀70年代建立的歐拉雙流體模型廣泛應用于核工業。Bendiksen 等[10]建立的OLGA模型在石油工業中被廣泛應用，是最早以雙流體模型為基礎開發并使用的瞬態計算代碼之一。Zheng 等[11]通過研究簡單起伏管路內的段塞流建立了一個SINK&SOURCE 模型。 Nydal 和Banerjee[12]，Taitel 和Barnea[13]也建立了段塞模型，以上模型都需要額外的段塞流參數，如段塞形成條件、段塞頻率、段塞長度等。

應用于雙流體模型的線性穩定性理論經常被用來確定分層流的穩定性。Taitel 和Dukler[14]將該理論應用于不考慮剪切應力的理想流體，得到非黏性Kelvin-Helmholtz（IKH）穩定性準則。該準則可以預測伯努利效應產生的吸力大于流體重力時氣液界面波的生長。Barnea 和Taitel[15]隨后通過對黏性流場的線性穩定性分析，得出黏性Kelvin-Helmholtz（VKH）穩定性準則。Issa和Kempf[16]論證了當氣液流速處于IKH 和VKH 準則之間時，使用交錯網格的雙流體模型能夠捕獲分層流過渡到段塞流過程中氣液界面產生的擾動。氣液兩相流在初始條件下自由發展，減少了對物理現象模型（流型轉變、段塞形成等）的依賴。Issa 等[16]利用此模型模擬了V 型兩相流起伏管道內的段塞頻率、段塞平均長度和持液率，得到與實驗數據一致的波動趨勢。

Renault[17]以Issa 的研究為基礎，基于IKH 和VKH準則實現了分層流過渡到段塞流的模擬，捕捉段塞前后界面運動過程，取得了較好的預測效果。盡管Renault 模型基于IKH和VKH 準則捕捉段塞前后液面變化，然而其求解過程中將液相方程轉化為淺水方程，并在單元格之間采用黎曼（Riemann）精確解，使得求解速度較慢。因此，需對模型進一步改進，使其保持精度的同時提高計算效率。

許仁義等[18-20]將行波法與Riemann 精確解相結合，對稀疏波采用單波近似，實現了淺水方程的快速求解，實現了高分辨率、高計算精度的效果。因此本文嘗試將行波法引入Renault 模型，建立新的段塞捕捉模型及求解方法。同時為保證行波法適用于所有計算單元，對可能出現的干區采用薄液膜進行簡化處理，在保證模型精度的條件下進一步提高求解速度。

1 段塞捕捉模型建立

1.1 模型基本方程

Renault 建立的段塞捕捉模型假設條件為：①液相不可壓縮；②理想氣相；③相對于液相動量，氣相動量可以忽略；④求解液相動量方程時，氣相為局部不可壓縮。計算域內網格被劃分成段塞網格和氣泡網格兩類。段塞網格存儲平均液相速度（Uslug）、氣泡網格存儲含液率（β）、平均液速（Ul）、氣體表觀流速（USg）、壓力（p）存儲在交錯網格上，計算網格如圖1 所示，模型方程如式(1)～式(5)。

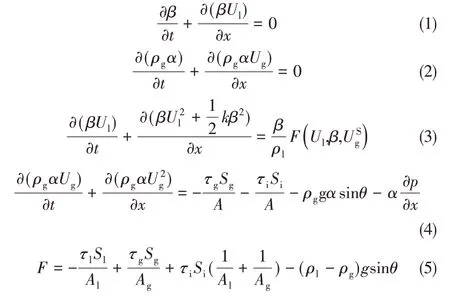
1.2 閉合關系式

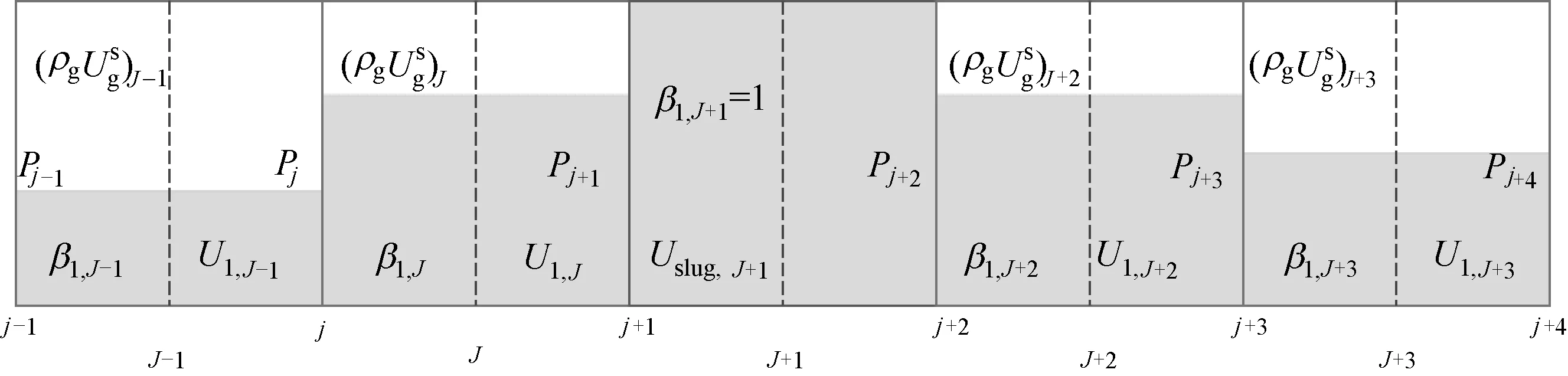
圖1 計算網格

液相和壁面、氣相和壁面以及氣液界面間的剪切應力關系如式(6)～式(8)。液相與壁面的摩阻系數、氣相于壁面的摩阻系數如式(9)和式(10)，氣液相界面摩擦因子采用由Cohen 與Hanratty[21]提出的常數值如式(11)，氣泡平移速度采用Bendiksen[22]關系式，如式(12)。

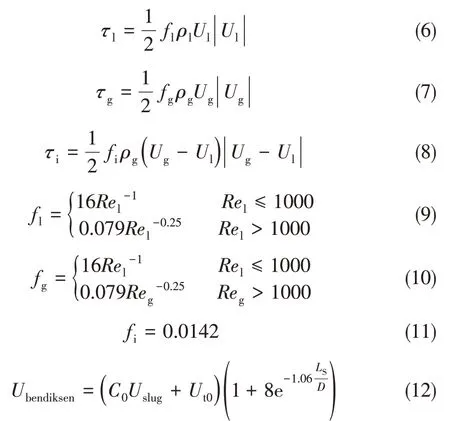
紊流情況下，根據弗魯德數（Fr）計算參數C0、Ut0。

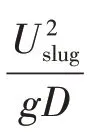
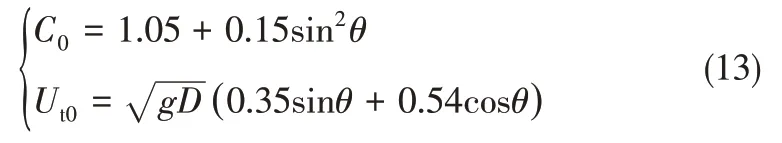
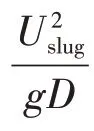
1.3 模型求解

Renault 模型求解過程中氣相和液相方程的求解是交替進行的。氣相方程采用一階迎風格式化簡為式(15)。

由于氣相方程符合三對角矩陣形式，因此采用追趕法即可求解每個網格中n+1 時刻的氣相狀態。

液相方程可化簡為淺水方程形式，如式(16)和式(17)。

液相求解過程較為復雜，采用戈杜諾夫（Godunov）方法[22]，在每個單元邊界求解淺水方程Riemann問題的精確解，進而構成整個流場的數值解[式(18)和式(19)]，求解過程如圖2（圖2中xj與xj+1左右兩側均為稀疏波）。

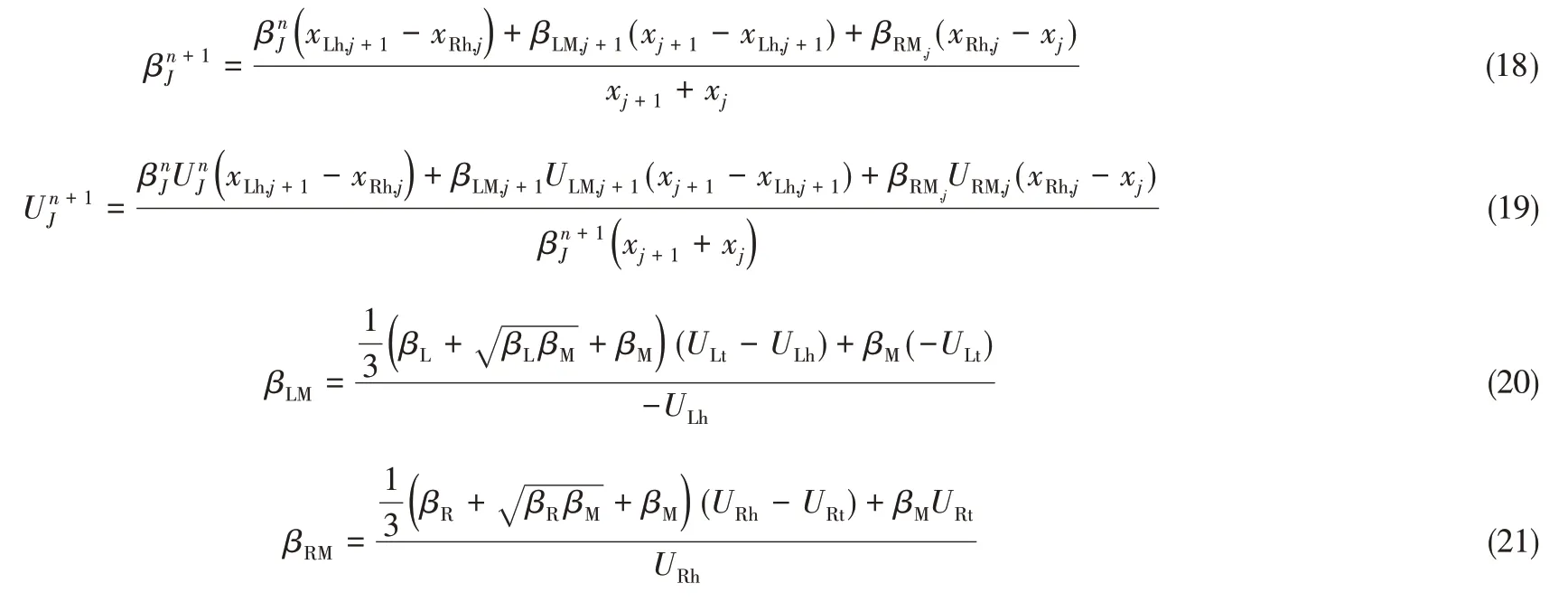
圖2 戈杜諾夫方法求解過程

1.4 模型簡化

由于Renault 模型中液相求解需要對網格邊界產生的稀疏波區域持液率（βLM、βRM）進行核算，計算量較大。為此，本文提出采用行波法求解單元邊界Riemann問題，對稀疏波采用單波近似，同時用薄液膜代替干區，使行波法適用于干區計算，從而簡化求解過程，提高計算效率。

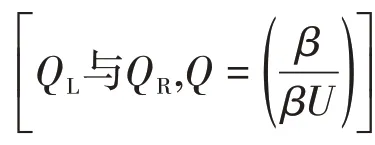
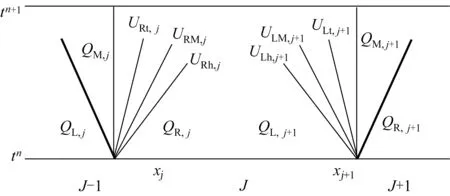
圖3 Riemann問題精確解結構

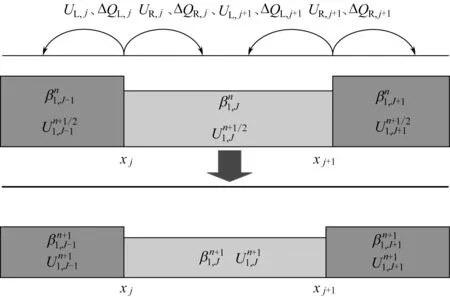
圖4 行波法求解過程

對比圖2、圖4 求解過程發現，對稀疏波采用單波近似，并用行波法求解液相方程極大地簡化了求解過程。淺水方程求解過程會出現干區情況，為使行波法適用于所有計算單元，使用薄液膜代替干區，薄液膜的液量來自相鄰單元。為了解行波法處理干濕邊界問題時的性能，采用一種長100m、寬1m、初速度為0、水面不連續的一維渠道淺水方程作為研究對象。用0.1m 的液膜代替干區，初始條件如式(22)。

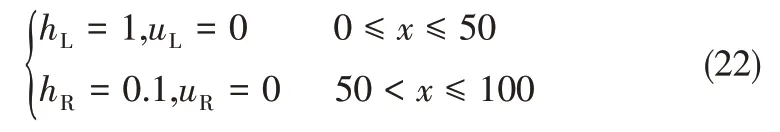
計算范圍x∈[0,100m]被分成100 個網格，空間步長dx=1m。潰壩初始時刻如圖5所示。初始時刻水面間斷處（x=50m）產生向左傳播的稀疏波和向右傳播的激波。圖6 為CFL=0.8、t=5s 時的計算結果。

從圖6可以看出，用薄液膜代替干區的簡化方法得到的數值解與精確解相一致，可以反映液相在干濕邊界的流動狀態。將Renault 模型單元邊界存在的干區均用薄液膜代替。此簡化處理使得行波法適用于所有網格計算，極大地提高了運算速度，簡化后的全新計算流程如圖7所示。

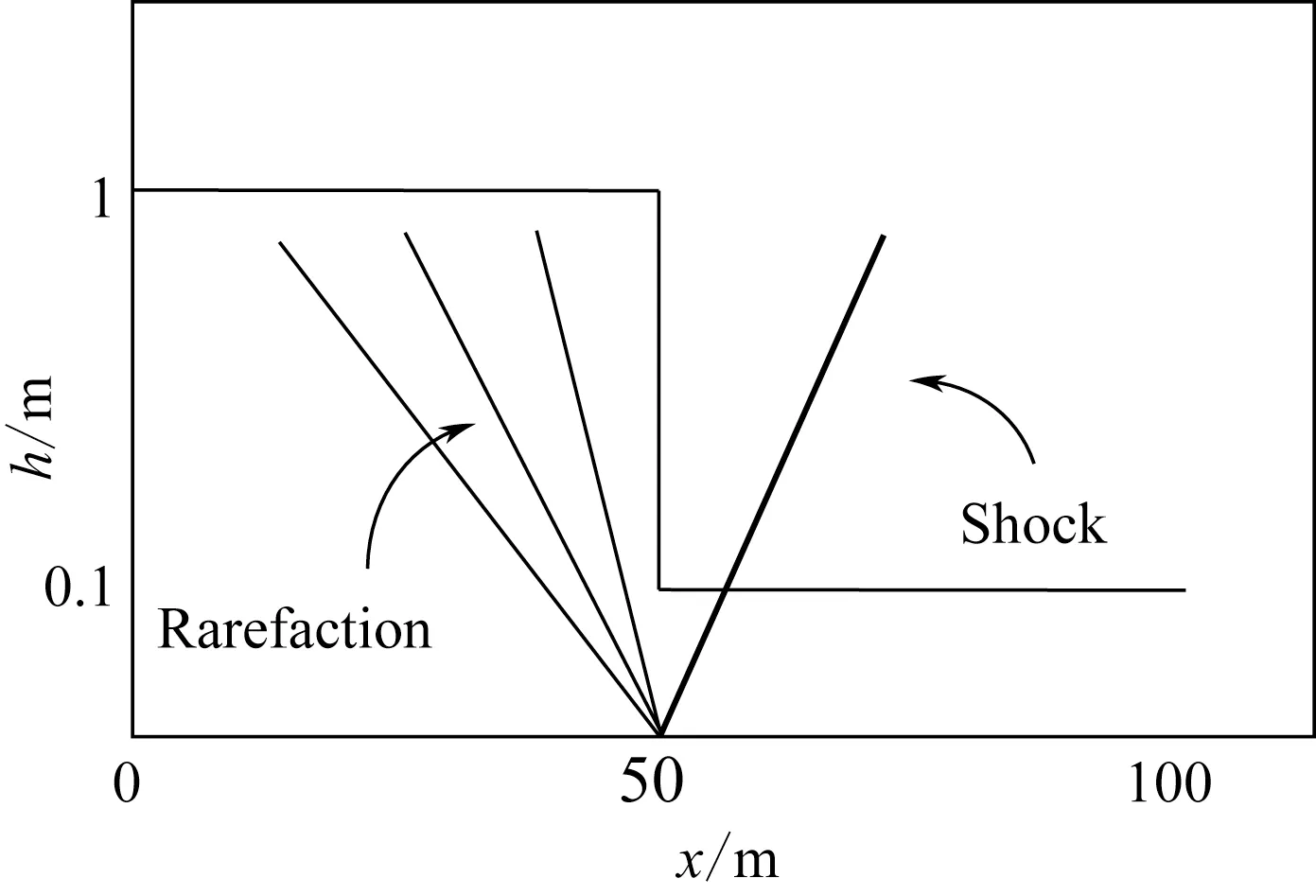
圖5 初始液面狀態

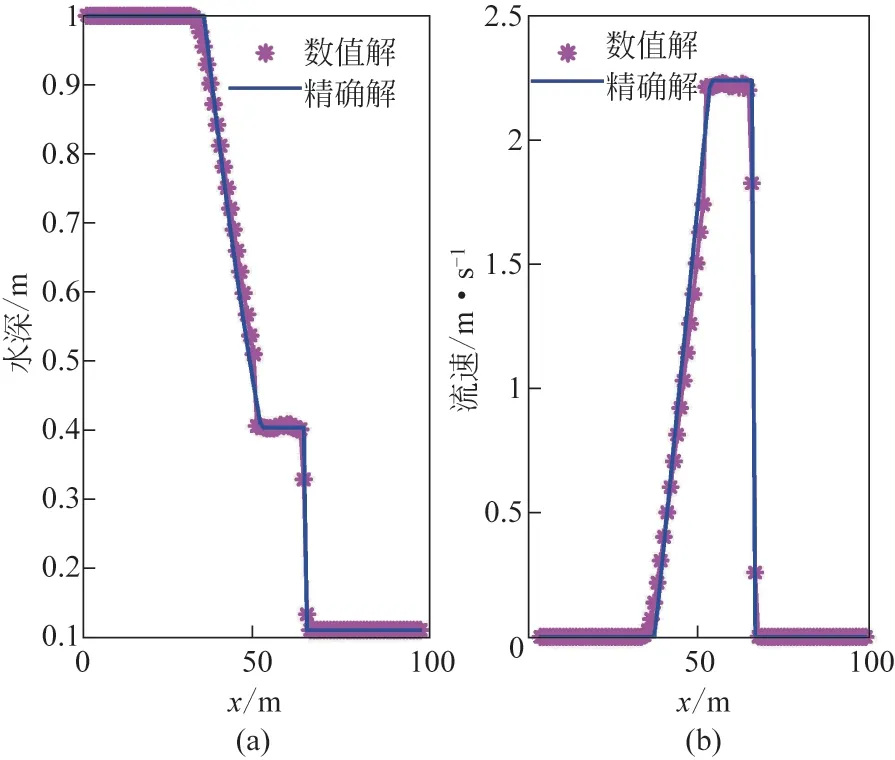
圖6 潰壩模擬

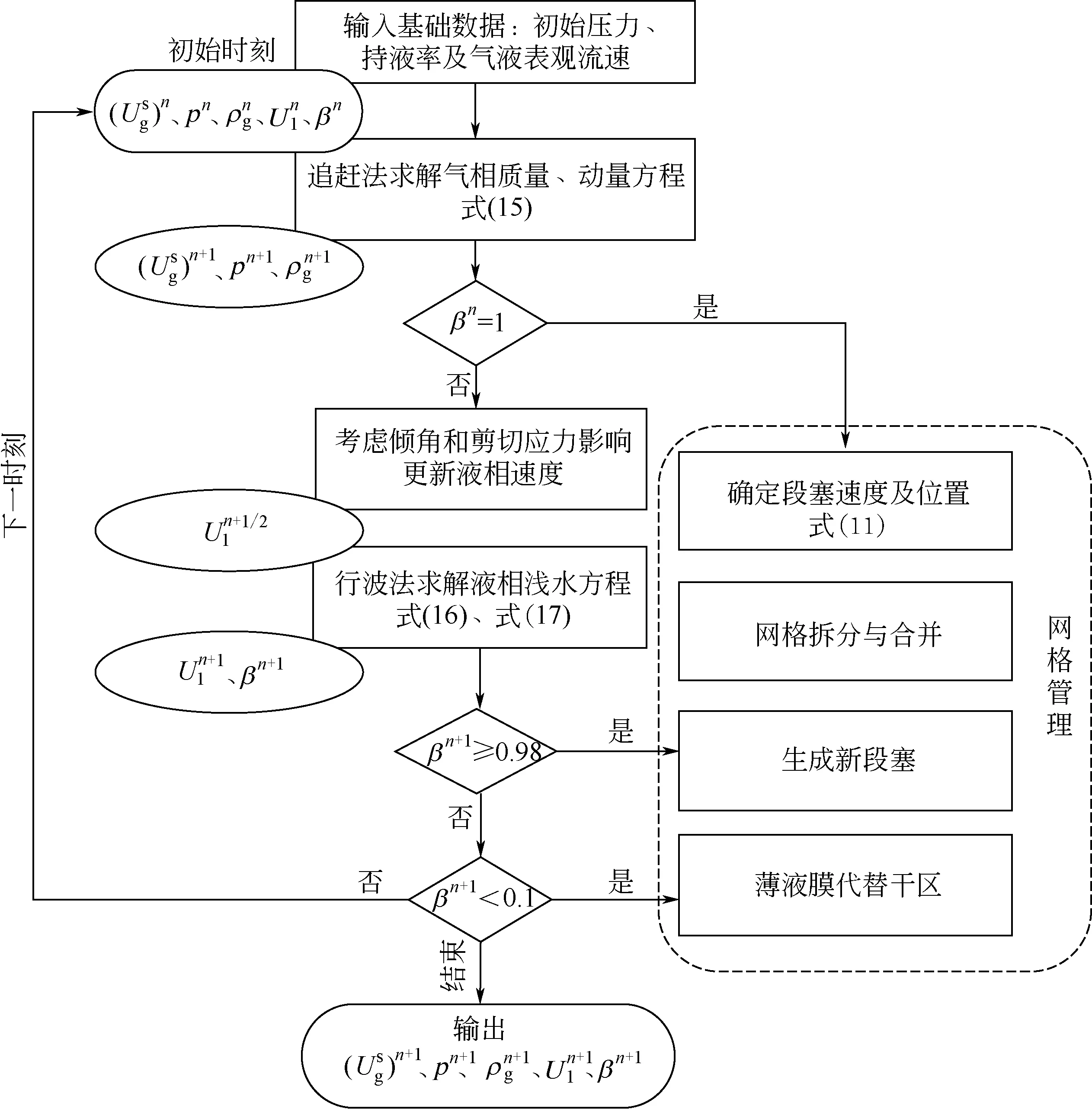
圖7 計算流程

實驗發現段塞運動過程中頭部呈豎直斷面、尾部呈曲面（圖8）。為使計算結果與實際段塞運動過程相一致，需對生成的段塞進行特殊處理。段塞頭部速度Ufront根據液體質量守恒核算，氣泡頭部速度UBendiksen由Bendiksen 關系式核算，計算過程如圖9。

圖8 段塞運動

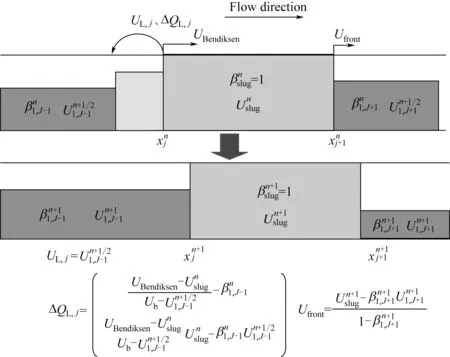
圖9 段塞計算過程

2 模型驗證

2.1 實驗系統

本實驗的介質采用空氣和水，實驗裝置示意圖如圖10 所示。實驗管道內徑D=40mm，總長45m，其中水平測試段管長10m。測試管段采用透明有機玻璃材質，以便觀察管內氣液流型變化。管道混合器出口處布置有壓力傳感器P0，水平段內布置有間距均為0.8m 的雙平行電導探針（CP1～CP3）與壓力傳感器（P1～P3）。采用Iotech6220 采集卡進行持液率與壓力信號的采集，采樣頻率為50Hz，采樣時間為60s。實驗中的氣體表觀流速范圍為0～4m/s，液體表觀流速范圍為0～1.6m/s。

2.2 實驗數據驗證

為驗證模型的段塞捕捉能力，以實驗管道為基準進行模擬計算。管道剖面尺寸如圖11，模型計算域為[0,10]m，網格寬度Δx=0.02m，管徑D=40mm，時間步長Δt=0.01s，模擬時間10min。氣體表觀流速范圍為0～4m/s，液體表觀流速范圍為0～1.6m/s。入口采用質量流量邊界條件，出口采用壓力邊界條件，計算結果如下。

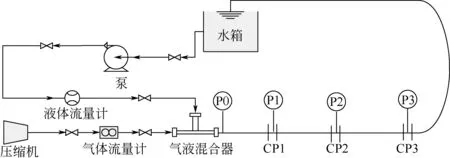
圖10 實驗裝置示意圖

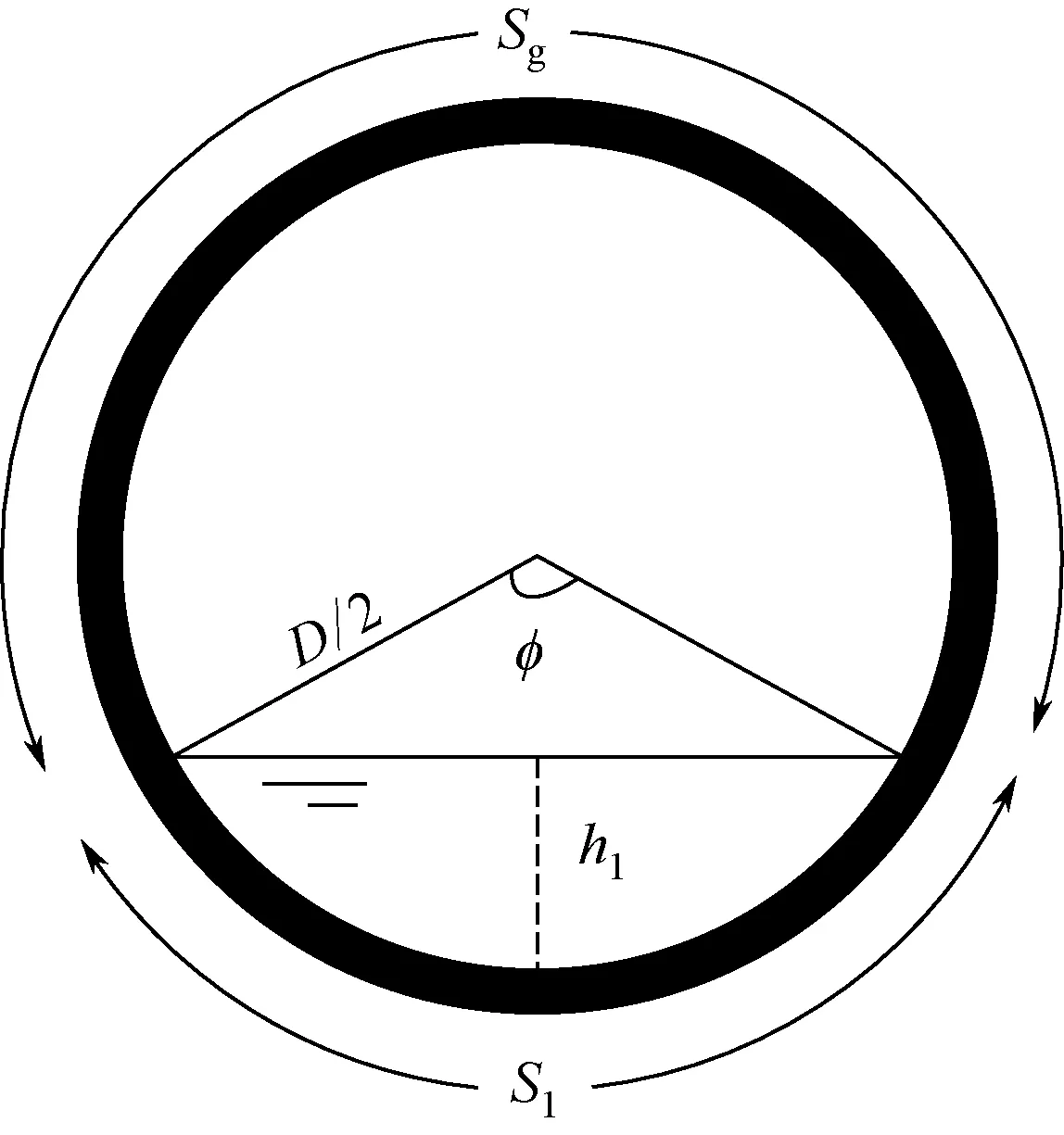
圖11 管道剖面示意圖

圖12 為氣體表觀流速0.9m/s、液體表觀流速0.45m/s、時間t=30s時的模擬結果。圖13為CP1處1min內實驗與計算持液率對比。從圖中可以看出，隨著管道長度的增加，液面漸漸產生波動，流型由分層流轉變為波浪流；隨著波動幅度的增大，流型進一步發展成為段塞流；計算CP1 處1min 內產生的段塞數略大于實測值，持液率變化與實測結果相一致，且段塞頭部呈豎直面，氣泡頭部呈曲面；本模型可以捕捉段塞流生成與發展過程，實現段塞流壓降精確計算。

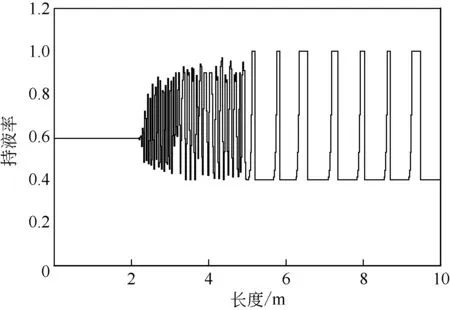
圖12 t=30s持液率計算結果

圖14、圖15 分別為模擬實驗工況30min 內的平均壓降、平均段塞長度值與實驗值對比。圖16為兩者計算值與實測值相對誤差概率密度分布。從圖中可以看出，壓降、段塞長度的相對誤差分別在25%、30%以內，且主要分布在20%以內，壓降計算準確度要高于段塞長度。

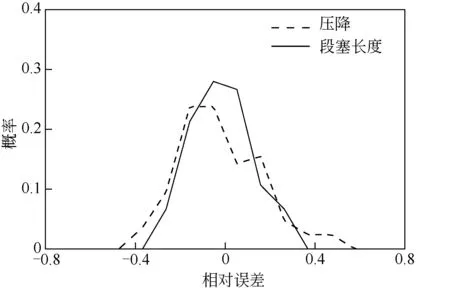
圖16 30min內壓降與段塞長度的相對誤差概率分布

為進一步了解本文模型簡化方法對計算效率的影響，對比Renault 模型與本文簡化模型在50、100、200、300、400 網格數下的計算耗時。計算硬件條件CPU 為Intel i7-6700 3.4GHz、內存為16GB，操作系統為64 位Windows 7，運算軟件為Matlab 2017，對比結果如圖17所示。

由圖17 可以看出，兩種模型的計算耗時與網格數均成正相關，隨著網格數的增加，計算量增大，耗時逐漸增加；當網格數較低時，兩種模型計算耗時差距較小，隨著網格數的增加，本文采用薄液膜代替干區與行波法求解液相方程組的簡化方法優勢逐漸明顯，運算時間相較于原模型平均減少28%。

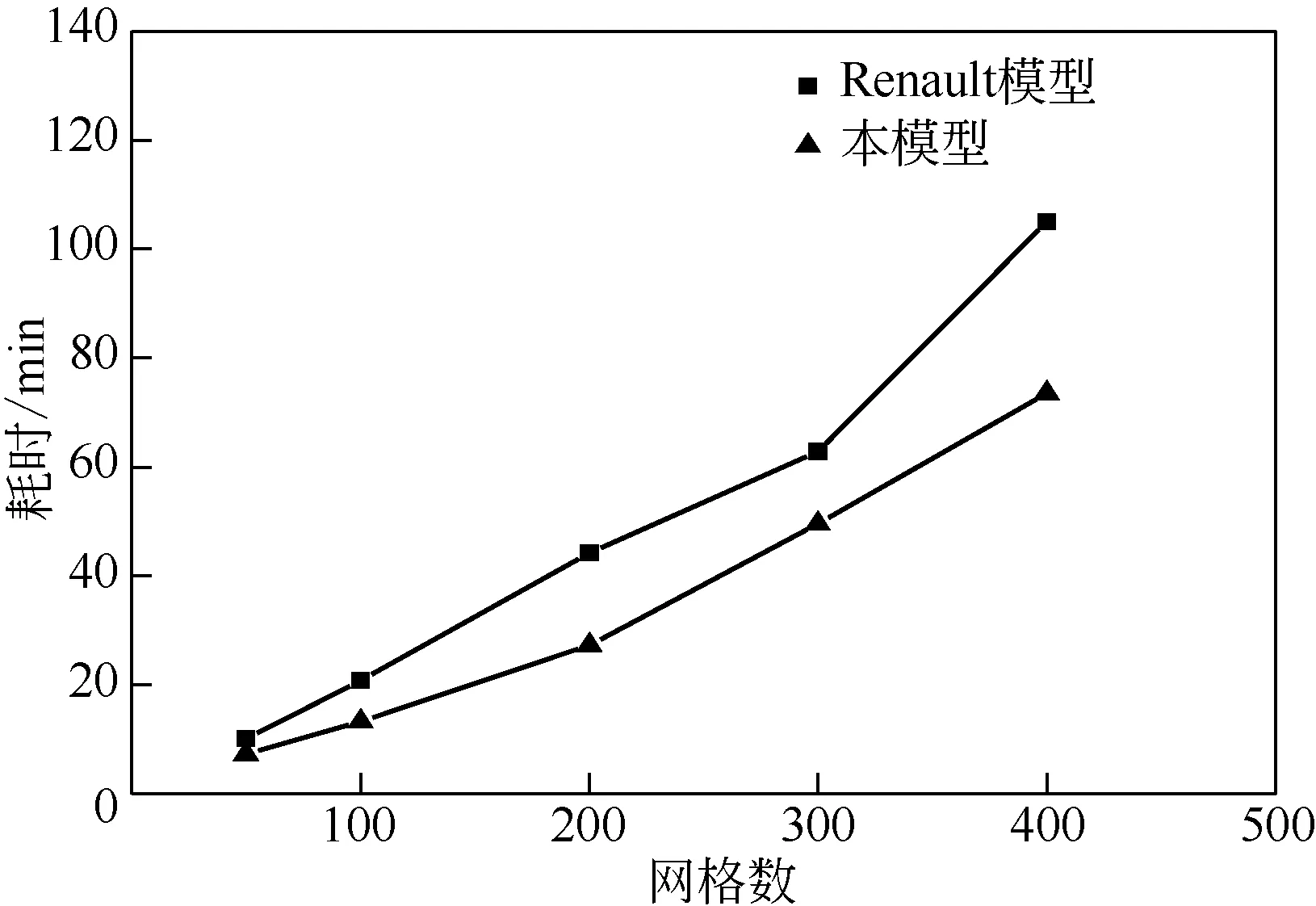
圖17 不同網格數下的計算耗時

3 結論

（1）本文將行波法引入到Renault模型求解中，對稀疏波采用單波近似，用Riemann近似解代替單元格之間的精確解，并用薄液膜代替干區，使行波法適用于所有計算單元，在保證計算精度的同時極大地提高了求解速度。

（2）將室內小型環道實驗數據與本模型計算結果對比，本模型可以模擬氣液兩相流由分層流發展到段塞流的物理過程，段塞頭部呈豎直面、氣泡頭部呈曲面，符合實驗觀察結果，持液率計算結果與實驗結果相一致，壓降、段塞長度計算相對誤差分別在25%、30%以內，且主要分布在20%以內。

（3）對比本模型與Renault 模型在不同網格數下的計算效率，本模型運算時間相比于Renault 模型平均減少28%，表明本文所提出的簡化方法極大地提高了計算效率，該瞬態段塞流捕捉模型可用于油氣管道段塞流的快速準確預測。

符號說明

A——管路橫截面積，m2

Ag，Al——氣相、液相所占的流通面積，m2

D——管內徑，m

Fr——Froude數

fg，fl，fi——氣壁、液壁和氣液相間摩阻系數

g——重力加速度，m/s2

J——網格單元

LS——段塞長度，m

n——表示時刻

p——管內的壓力，Pa

Rel，Reg——液相雷諾數、氣相雷諾數

Sg，Sl，Si——氣壁、液壁與氣液相間濕周，m

Δt——時間步長，s

Ug，Ul——氣相真實速度、液相真實速度，m/s

，——氣相表觀速度和液相表觀速度，m/s

Δx——空間步長，m

α——截面含氣率

β——截面含液率

θ——管道傾斜角度，(°)

?——液面夾角，(°)

μl，μg——氣相和液相的動力黏度，Pa·s

ρl，ρg——氣相和液相密度，kg/m3

σ——表面張力，N/m

τg，τl，τi——氣壁、液壁和氣液相界面的剪切應力，Pa

下角標

g——氣相

i——氣液相間

l——液相

L——左側

M——中間

R——右側