控制變量法的失當套用例析

唐玉蘭 羅國忠

摘? ?要：控制變量法是一種應用廣泛的探究方法，但在教學中存在部分教師不顧實際情況而盲目套用這一方法的現象。在一節課例“探究杠桿平衡條件”中，就存在刻意套用控制變量法的現象，并伴隨暗含問題搖擺混同、實際問題主次顛倒、研究變量隨意取舍等失當問題。文章針對這些失當問題，提出了改進設想，使問題切合實際，方法有的放矢。

關鍵詞：杠桿平衡條件;控制變量法;套用;主次顛倒

中圖分類號：G633.7 文獻標識碼：A ? ? 文章編號：1003-6148（2020）7-0069-4

控制變量法是非常重要的科學探究方法之一，應用非常廣泛，按理說身為教者的教師應該對其使用得心應手。但筆者發現，在教材中沒有明示控制變量法之處，有些教師自我發揮，還是會出現一些問題。例如，有些教師不管什么探究內容，總是想方設法把問題設計成“某某與什么有關”“影響某某的因素有哪些”等形式，然后套用控制變量法進行探究，似乎控制變量法是一種萬能方法，能探究所有問題，這其實是對控制變量法的夸大、神化而導致的應用失當。

科學史表明，任何研究方法都有其相對應的研究問題和應用規則，沒有哪個方法是放之四海而皆準的。因此，本文首先厘清什么是控制變量法？然后以此分析一節課例“探究杠桿平衡條件”，看看這節課例是如何套用控制變量法？由此產生什么問題？

1? ? 什么是控制變量法

在多變量（因素）問題中，一個研究對象可能受到多個變量的影響。為了弄清研究對象與這些變量的關系，我們把多變量問題變成多個單變量問題，首先逐個研究單個變量對研究對象的影響，即每次只改變某一個變量，同時控制其他變量不變;最后把這些單變量結論綜合起來，得出總結論。這樣的研究方法就是控制變量法，它有如下幾個特征。

研究問題。多變量問題的特征比較明顯，其標志性形式如“某某研究對象與哪些變量（因素）有關或無關”“如果有關，是什么關系”等。典型例子如“影響滑動摩擦力的因素有哪些”“壓強與壓力、受力面積有什么關系”等。

研究變量。把可能影響研究對象的變量（因素）稱為自變量，而可能受自變量影響的研究對象稱為因變量。應用控制變量法時，自變量要互相獨立，互不影響。如果有些自變量可能互相影響，則需篩選、排除或整合，這是應用控制變量法的難點之一。

操作程序?？刂谱兞糠ǖ牟僮鞒绦蚴牵阂淮沃桓淖円粋€自變量，而其他自變量保持不變。例如，y與x1、x2、x3有什么關系？首先研究y與x1的關系，只改變x1，同時x2、x3保持不變。然后，又依次輪換。

2? ? 一節課例“探究杠桿平衡條件”

下面是一位教師執教“探究杠桿平衡條件”時的探究程序和關鍵細節[1]。

2.1? ? 問題、猜測

教師讓學生相互扳手勁，然后要求學生根據活動“猜出影響杠桿平衡的條件”，并引導學生猜測：①杠桿平衡條件與力的大小、方向、作用點有關;②杠桿平衡條件與力的大小、力臂的長短有關。

2.2? ? 設計、實施

學生猜測后，教師明確要求采用控制變量法，設計探究程序，探究杠桿平衡條件。

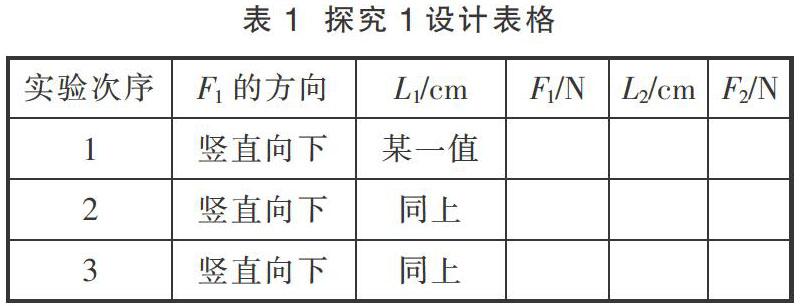
探究1：教師設計表1，探究杠桿平衡條件與作用在杠桿上某個力大小的關系。

具體操作：在杠桿的左端確定一點（L1）掛上鉤碼，同時在杠桿右端也掛上鉤碼，直至杠桿重新平衡。然后，在L1不變時，通過增減鉤碼改變F1的大小，同時在杠桿的右端移動或增減鉤碼，達到每次改變F1的大小時都能使杠桿平衡。實驗進行三次，數據填入表1。教師引導學生得出結論1——當作用在杠桿上的某個力的作用點、方向沒有改變，只有大小變化時，杠桿的平衡條件是F1×L1=F2×L2。

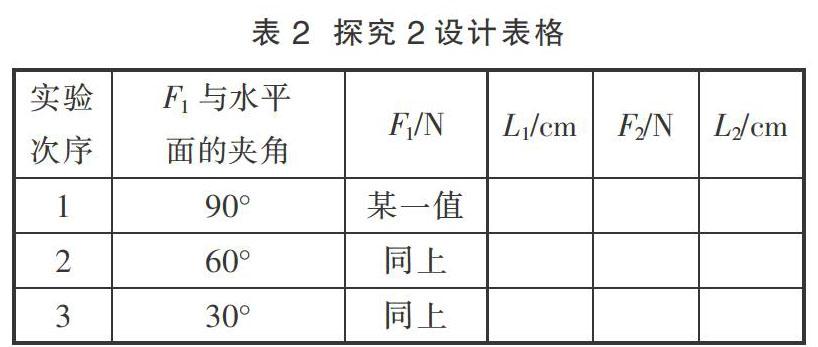
探究2：教師設計表2，探究杠桿平衡條件與作用在杠桿上某個力的方向的關系。

具體操作：類似地，在杠桿的左端確定一點（L1）掛上鉤碼，同時在杠桿右端也掛上鉤碼，直至杠桿重新平衡。然后，在F1大小不變時，通過改變鉤碼與水平面的夾角改變F1的方向，同時在杠桿的右端移動或增減鉤碼，達到每次改變F1的方向時都能使杠桿平衡。在分析實驗數據的基礎上，教師引導學生得出結論2——當作用在杠桿上的某個力的作用點、大小沒有改變，只有方向變化時，杠桿的平衡條件是F1×L1=F2×L2。

探究3：有了兩次經驗后，教師讓學生自主探究杠桿平衡條件與作用在杠桿上某個力作用點的關系，并得出結論3——當作用在杠桿上的某個力的大小、方向沒有改變，只有作用點變化時，杠桿的平衡條件是F1×L1=F2×L2。

總結論：

總結三個分結論，得出總結論：無論作用在杠桿上的某個力的大小、方向、作用點怎樣變化，杠桿的平衡條件都是F1×L1=F2×L2。

3? ? 案例存在的問題分析

3.1? ? 暗含問題搖擺變化、相互混同

對于杠桿，初中物理課程標準的目標要求非常明確，即“通過實驗，探究并了解杠桿平衡條件”，其知識目標是“杠桿平衡條件”，對應的探究問題就應是“杠桿平衡條件是什么”，這個問題本應貫穿始終，但這節課卻還伴隨著其他暗含問題，而且搖擺變化，有些甚至相互混同。所謂暗含問題，指教師并不明說，但可以從其要求中推斷出來的問題。

在學生扳手勁活動后，教師的最初要求是“猜出影響杠桿平衡的條件”，并引導學生猜測：①杠桿平衡條件與力的大小、方向、作用點有關;②杠桿平衡條件與力的大小、力臂的長短有關。表面上，這里沒有明示的問題，但從最初要求“猜出影響杠桿平衡的條件”可以看出，其暗含問題是“影響杠桿平衡的條件是什么”——問題1;從其引導的猜測可以看出，其暗含問題又變成“杠桿平衡條件與哪些變量有關”——問題2。首先，從形式上看，問題1和問題2都是與控制變量法匹配的多變量問題。其次，問題1和問題2并不是同一個問題，因為問題1的因變量是“杠桿平衡”，自變量是“條件”;問題2的因變量是“杠桿平衡條件”，自變量是“變量”。顯然，兩者的因變量完全不同，自變量也完全不同。但不難看出，教師已經在無意識中把兩個問題視為同一個問題，即把“杠桿平衡”當成“杠桿平衡條件”，把“條件”當成“變量”。這顯然是概念混同導致了問題混同。

在學生猜測后，教師接著明確要求用控制變量法，設計探究程序，探究杠桿平衡條件。表面上這里也沒有明示的問題，但也可以從其要求“探究杠桿平衡條件”看出，其暗含問題變成了“杠桿平衡條件是什么”——問題3，這才是這節課本該研究的正確問題。問題3和問題1、問題2看似差不多，其實差異很大。問題2問“杠桿平衡條件與各個變量的獨立關系”，而問題3問“這些變量整體滿足什么條件時，杠桿才會達到平衡狀態”，因此，問題3和問題2完全不是同一個問題，問題3和問題1也不是同一個問題。

設計探究程序時，在三個變量中（F1的三要素），每次改變一個變量，其他兩個變量控制不變。盡管問題也沒有明示，但從其設計也可以看出其暗含問題變成了“杠桿平衡條件與力的三要素是否有關”——問題4。問題4和問題2看似差不多，都屬于多變量問題，但這里問題4的多變量明確縮減為三個變量（力F1的大小、方向、作用點），而不是原來猜測的五個變量（①力的大小、方向、作用點;②力的大小、力臂的長短）。

實施探究時，采用了控制變量法，根據數據得出三個分結論，并綜合成總結論，即“無論作用在杠桿上的某個力的大小、方向、作用點怎樣變化，杠桿的平衡條件都是F1×L1=F2×L2”。該結論可分成兩部分，分別回答了暗含問題3“杠桿平衡條件是什么”、暗含問題4“杠桿平衡條件與力的三要素是否有關”。

從以上分析看出，這節課本應圍繞問題3貫穿始終，但其暗含問題卻不斷搖擺變化，而且相互混同，缺乏清晰的問題主線。由于這些暗含問題是潛藏的，教師很有可能并未意識到它們的存在及其變化、混同。

3.2? ? 實際問題主次顛倒、喧賓奪主

如果教師未意識到其暗含問題的多變、混同，那么其真正想研究的實際問題究竟是什么呢？不妨分析這節課得出的最終結論（達成的總目標），即“無論作用在杠桿上的某個力的大小、方向、作用點怎樣變化，杠桿平衡條件都是F1×L1=F2×L2”，如前面分析，可以看出它回答兩個問題，即“杠桿平衡條件是什么”“杠桿平衡條件與力的三要素是否有關”，這就是教師真正想研究的實際問題。

如果一定要研究這兩個問題，那么對照課標要求可知，前一個問題毋庸置疑是必須研究的主要問題，后一個問題是可選的次要問題。主要問題本應下重手研究，即應通過實驗得出幾組“F1、L1、F2、L2”數據，然后對數據進行分析處理，設法找出其潛藏的規律（條件）。但由于數據繁雜，表面看似毫無規律，如果沒有提示引導，學生僅憑己力，一般不知道從何著手，難以得到正確結論“F1×L1=F2×L2”。因此，如何引導學生分析、處理數據，歷來就是這節課的重點、難點、亮點之一。然而，縱觀整個探究過程，看到更多的是教師把心思花在設計并探究其創新點“杠桿平衡條件與力的三要素是否有關”，反倒沒有看到如何分析處理棘手的“F1、L1、F2、L2”數據，“杠桿平衡條件”更像是可以輕易附帶出來的副產品。

從以上分析看出，教師把課標未作要求的“杠桿平衡條件與力的三要素是否有關”提升為問題主線，把課標要求的“杠桿平衡條件是什么”降格為附屬問題并塞進其中，造成了主次顛倒、喧賓奪主的邏輯錯位。究其原因，是教師要突出控制變量法的應用，所以就刻意設計并突出“杠桿平衡條件與力的三要素是否有關”問題，這樣就能用控制變量法實施探究。這種做法貌似體現了不拘泥于課標和教材的創新精神，殊不知違背了知識邏輯，脫離了實際情況，無異于“削足適履”。

3.3? ? 研究變量隨意取舍、缺乏整合

再從研究變量的角度，來看看教師對控制變量法的應用是否適當？

教師引導學生兩次猜測：①杠桿平衡條件與力的大小、方向、作用點有關;②杠桿平衡條件與力的大小和力臂的長短有關。接著，明確要求用控制變量法進行研究。那么，按照控制變量法的規則，既然總共猜測了五個變量，接下來就應該探究杠桿平衡條件與這五個變量的關系。但實際上教師卻只探究“杠桿平衡條件與某個力（F1）的大小、方向、作用點的關系”，根本不提“杠桿平衡條件與力的大小、力臂的長短的關系”，而且沒有任何解釋說明。這種做法顯然違背控制變量法的應用規則，同時也會給學生示范一個不良行為：研究變量可以隨意取舍。

其實，教師引導下的兩次猜測結果貌似不同，其實完全相同。因為第一次猜測中的“力的方向、作用點”可整合為“力臂的長短”，這樣兩次猜測的結果其實完全一樣，都是“力的大小、力臂的長短”。但教師卻不分析、不整合，硬是掰成兩個“不同”的猜測，這樣的做法也同樣不符合控制變量法的應用規則。

如果聯系前面對實際問題的分析，不難看出教師對變量的隨意取舍、缺乏整合，其實與實際問題的主次顛倒是一脈相承的。縱觀整個探究過程，不難看出教師的設計意圖，即把“力的大小、方向和作用點”歸口到“杠桿平衡條件與力的三要素是否有關”，把“力的大小、力臂的長短”歸口到“杠桿平衡條件是什么”，所以才會把同一個猜測結果硬生生地掰成了兩個貌似不同的猜測結果。

4? ? 改進設想

首先，在學生扳手勁活動的基礎上，引導猜測可能有哪些因素影響杠桿平衡（不是杠桿平衡條件）？假如學生的確猜測了“①力的大小、方向、作用點;②力的大小、力臂的長短等”，那教師就應該引導學生分析、梳理這些變量，使他們認識到這些變量相互之間并不完全獨立，而是可以整合為兩個變量：力的大小、力臂的長短，而杠桿所受的力分為動力、阻力，相應力臂分為動力臂、阻力臂。接著，由教師引出新問題“動力、阻力、動力臂和阻力臂在滿足什么條件時可以使杠桿平衡”——問題A。要探究問題A，不宜使用控制變量法，而應該用比較法，即比較杠桿平衡時四個變量的整體關系。比較法對操作過程、變量是否控制不作限制，靈活多樣，只要出現平衡結果即可，即不管過程只要結果，類似“八仙過海，各顯神通”。生活例子比比皆是，如用錘子撬鐵釘，屬于控制一個量（阻力）不變，變化另外三個量;用桿秤稱東西，屬于控制兩個量（阻力臂和動力）不變，變化另外兩個量;鍋爐的保險閥門，屬于控制三個量（阻力、阻力臂、動力臂）不變，變化另一個量;坐蹺蹺板，甚至四個變量都同時變化，也能達到平衡。

接著，如果學生的確發自內心提出“杠桿平衡條件與某個力的大小、方向、作用點是否有關”——問題B，那就不妨作為問題延伸進行研究，用證據回應學生的關切，沖擊學生的前概念，這也是尊重學生主體地位的體現。這時，就可以像課例中那位教師所做的那樣，通過控制變量法進行研究。

在以上設計中，問題A是重點，是保底基礎，問題B是延伸、可選，兩者指向不同、層次分明;相應的比較法、控制變量法也有的放矢，各為其主，服務各自問題。方法是為問題服務的，不能為了套用某個重要方法而刻意設計與其匹配的探究問題，甚至把真正的主要問題降格為附屬問題。那樣的“削足適履”既不利于培養學生發現問題、提出問題的能力，也不利于培養學生正確應用科學方法的意識和能力。

參考文獻：

[1]魏喜武.“探究杠桿平衡條件”的教學設計[J]. 物理教學，2012，32（1）：36-38.

（欄目編輯? ? 張正嚴）

收稿日期：2020-03-10

作者簡介：唐玉蘭（1963-），女，中學特級教師，主要從事中學物理教學研究，享受政府特殊津貼;羅國忠（1968-），男，教授，主要從事中學物理教學研究。