基于薄層單元法的彈體與引信系統螺紋連接模擬參數識別

鄢阿敏， 王曉鋒， 王健， 皮愛國， 黃風雷

(1.北京理工大學 爆炸科學與技術國家重點實驗室， 北京 100081； 2.北京系統工程研究所， 北京 100034)

0 引言

螺紋連接具有強度高、連接可靠、拆卸方便等優點，是組合結構里面一種廣泛應用的連接形式，侵徹彈體與引信的連接形式一般為螺紋連接。由于螺紋接觸含有許多不確定因素，導致了引信體振動響應無法準確預測。眾所周知，螺紋連接不確定性因素的主要來源是接觸剛度與摩擦阻尼兩方面的非線性因素[1]。由于常用模態分析軟件無法定義非線性因素，通常在數值分析時將螺紋連接簡化為固連狀態或定義為簡單的實體螺紋接觸，這種處理方式雖然極大地提高了計算效率，但是造成計算結果比實際值偏大。在高速侵徹多層硬目標信號識別領域，準確評估彈體與引信系統振動響應特性尤為重要。為提高仿真模型的計算精度，需要在仿真模型中對螺紋連接的接觸剛度與阻尼進行準確的模擬。因此探索出一種針對螺紋接觸準確的建模方式對研究彈體與引信系統振動響應具有十分重要的意義。

針對螺紋連接仿真建模，許多學者開展了工作。Mackerle[2]對1990年～2002年12年間出版的各種連接類型在不同加載狀態下有限元建模方式進行歸納與總結，其中大量工作是關于螺紋連接建模分析的。也有一些學者開展了關于螺紋連接靜態行為的研究工作[3-4]，還有一部分工作是針對螺紋動態特性進行開展的。例如：Zhang等[5]通過建立實體螺紋的方式對螺紋碰撞過程進行研究,得出了螺紋連接的碰撞頻率；Brutti 等[6]采用有限元模型對管螺紋的動態性能進行了研究，表明螺紋管構件的動態特性對結構的強度影響至關重要。

在組合結構動態響應仿真建模這一領域，許多學者就如何對連接界面準確表征這一問題進行了大量的探索，尤其集中在以薄層單元表征接觸界面的研究內容上。這其中代表性的工作陳述如下：Desai[7]1984年首次提出薄層單元建模概念，通過賦予薄層單元法向接觸剛度與剪切剛度來表征巖石、土壤接觸界面；Bograd等[8]對接觸界面模擬方式進行分析比較，闡述了薄層單元建模方式的優勢；Iranzad等[9]為表征局部非線性剛度與阻尼對螺栓搭接組合結構響應的重要影響，采用薄層虛擬彈塑性材料對接觸界面進行建模；姜東等[10]針對螺栓連接建模與參數識別問題開展研究，提出了螺栓連接結構接觸面力學性能識別方法；Zhao等[11]采用薄層單元模擬螺栓連接接觸剛度，得出螺栓預緊力對螺栓界面接觸剛度影響的一般規律；Adel等[12]采用一個雙連接薄層單元模型模擬混合結構中螺栓連接界面，基于該模型計算了混合螺栓連接結構的模態頻率，該模型可用于復雜結構和大型結構的混合節點界面的模態分析中；Lothar等[13]將薄層單元應用于發電機雙盤轉子收縮接頭有限元模型中，并將試驗獲取的連接阻尼與剛度參數耦合到層單元模型中，該模型可以作為預測發電機響應特性的工具；Alamdari等[14]將薄層單元引入螺母接口相互連接螺紋管有限元分析中，薄層單元采用非線性本構模型表征非線性狀態下節點的能量耗散和軟化現象。綜上所述，對于螺紋連接仿真分析，若是分析靜態與動態加載下力學行為，主要通過接觸的設置來表征非線性因素。如果對模態分析與頻率響應分析等動力學響應問題的研究，通過在接觸界面引入薄層單元表征非線性因素，這種方式目前主要應用于模擬螺栓連接接觸界面，并取得了比較好的效果。所以本文提出將薄層單元建模的方式應用于螺紋連接結構中，來解決螺紋動力學分析過程非線性因素無法識別的問題。

本文將薄層單元引入仿真建模中，來合理有效地模擬螺紋連接接觸剛度與摩擦阻尼等非線性因素的影響，仿真計算精度得到顯著改善。首先采用試驗方法研究松、緊不同連接狀態對模態頻率與頻率響應曲線的影響；其次利用多點約束(MPC)技術建立了螺紋連接的薄層單元模型，采用Nastran設計靈敏度分析模塊，對薄層單元的材料參數進行識別，基于試驗獲得的模態頻率與頻率響應曲線對識別后的薄層單元材料參數進行驗證；最后將薄層單元建模方式推廣應用于彈體與引信螺紋連接結構中。

1 薄層單元基本理論

采用薄層單元模擬螺紋連接接觸面，薄層單元尺寸l×s×t,其中l為薄層單元的長度，s為薄層單元圓周長度，t為薄層單元的厚度。根據虛位移原理，得虛功方程為

(1)

式中：V1為薄層單元在局部坐標系下的體積；σ為單元的應力；ε為單元的應變；{u}n為節點位移；K為薄層單元剛度矩陣，可通過等參變換計算：

(2)

B為變換矩陣，D為本構矩陣，ξ、η、ζ為自然坐標符號，J為雅克比矩陣，表征局部坐標與自然坐標的偏微分關系。在自然坐標系下，數值積分形式更簡便，可以將雅克比矩陣J進一步簡化為

(3)

(3)式代入(2)式中，可得到薄層單元剛度矩陣K的數值計算表達式為

det([J(ξi,ηj,ζk)])wζ,iwη,jwξ,k，

(4)

式中：wζ,i、wη,j、wξ,k為高斯積分權函數。

對于薄層單元，薄層單元的厚度t遠遠小于另兩個方向的特征尺寸l和s，根據Desai[7]的描述，采用泊松比為0的材料本構關系時，薄層單元法向剛度與切向剛度將會解耦，單元的面內應變分量(εx,εy,γxy)和應力分量(σx,σy,τxy)將被忽略。若接觸的法向{e}n和兩個切向{e}tx與{e}ty分別定義為薄層單元局部坐標系的z軸、x軸、y軸方向，根據以上分析，設連接界面法向與切向接觸性能相互獨立，兩個切向的接觸性能具有一致性，表征界面接觸性能的薄層單元本構方程為

(5)

式中：Esn、Gst分別是薄層單元的法向彈性模量和切向剪切模量。

在有限元計算中，若采用各向同性材料模擬薄層單元，其本構方程為

(6)

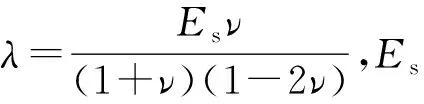
根據薄層單元的基本理論，εx=εy=εxy≈0，材料的本構方程將退化為

(7)

各向同性材料僅含兩個材料參數：彈性模量Es和剪切模量Gs. 在動力學仿真分析過程中，彈性模量與剪切模量影響模型的模態剛度，密度影響模型的模態質量，所以采用各向同性材料進行表征薄層單元模型，只需要確定薄層單元密度與彈性模量(或剪切模量)兩個參數。后面將基于模態試驗結果，將薄層單元的密度與彈性模量設置為設計優化變量，采用Nastran設計優化模塊對薄層單元的材料參數進行識別。

2 螺紋試件與無螺紋試件模態試驗研究

2.1 試驗裝置

為了給薄層單元建模參數的確定提供試驗數據支撐，開展螺紋連接組合結構的模態試驗。試驗試件由兩段空心圓柱管通過螺紋連接組成，如圖1所示。螺紋規格M36×2-6H/6g-40，內、外螺紋之間為間隙配合，6級加工精度，螺距為2 mm，旋合長度為40 mm. 為了驗證仿真計算螺紋的材料參數，設計同尺寸無螺紋試件同組進行試驗。

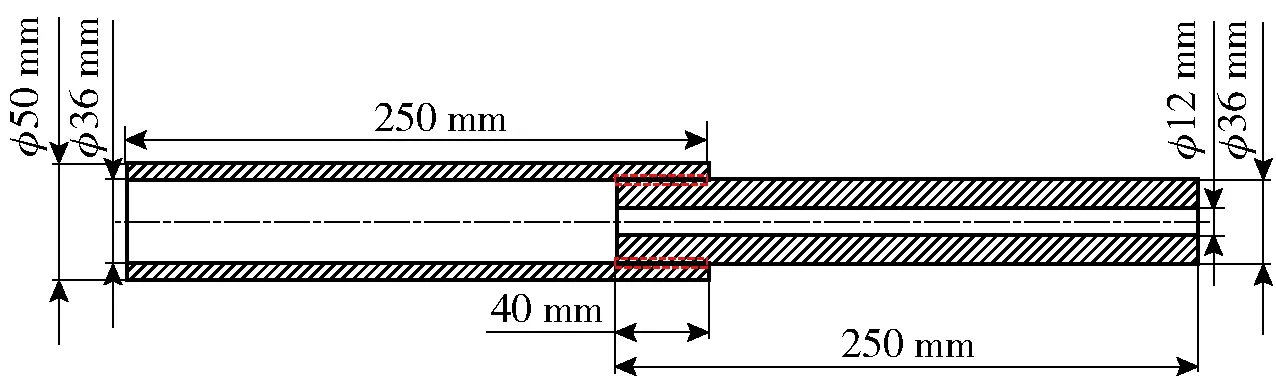
圖1 螺紋連接Fig.1 Thread connection

田晶等[15]采用多種懸掛方式與彈性支撐方式進行自由模態試驗，表明采用彈性繩懸掛的方式最接近自由邊界狀態，參考該方法，本文采用彈性繩對試件進行懸掛來模擬自由邊界條件。利用電磁激振器對螺紋試件進行激勵，如圖2激振器與傳感器分布示意圖所示，激勵點選擇在Z1位置處。兩個三向加速度傳感器粘貼在試件的A1與A2位置。利用比利時LMS公司模態分析軟件進行輔助測量與分析，選擇正弦掃頻信號作為激勵信號；采用1個16通道的模態分析儀接收和處理信號。模態分析儀產生的正弦掃頻信號經過運算放大后輸入電磁激振器，激振器接收信號產生激振力，激振器連接桿端部安裝有力傳感器，采集激振力傳入模態分析儀中，這樣就形成對激振力的反饋回路控制。

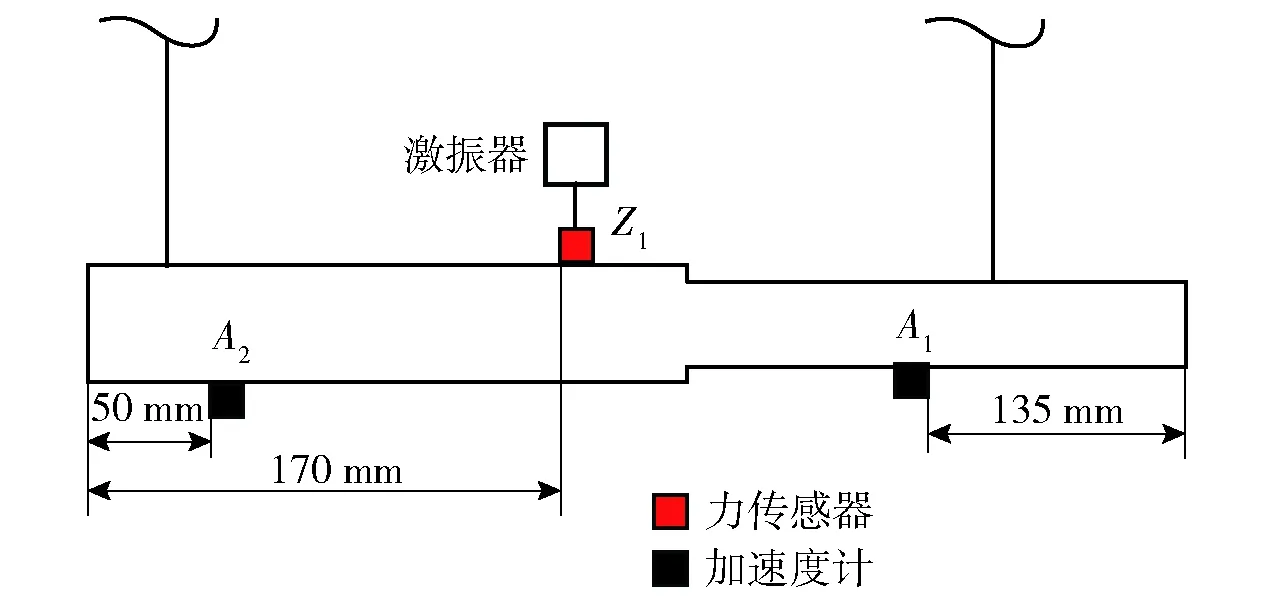
圖2 激振器與傳感器分布示意圖Fig.2 Schematic diagram of exciter and sensor layout

2.2 試驗過程與結果分析

2.2.1 無螺紋試件的模態試驗

無螺紋試件不含非線性因素。試驗中選擇正弦掃頻信號為激勵信號，該類掃頻信號可以保證測試的重復性，能夠很方便地測出模態頻率與頻率響應曲線[16]。掃頻范圍為100～5 000 Hz，保證了掃頻范圍能夠覆蓋結構前3階模態頻率，掃頻速度為10 Hz/s，激勵力的幅值為0.1 N. 端部A2處測量得到的前3階頻率響應曲線如圖3所示，前3階模態頻率分別為938.3 Hz、2 669.8 Hz、4 582.5 Hz. 試驗結果表明，頻率響應曲線存在明顯的尖峰，且曲線關于共振峰是嚴格對稱的，說明各階模態阻尼較小，頻率響應曲線具有明顯的線性特征。

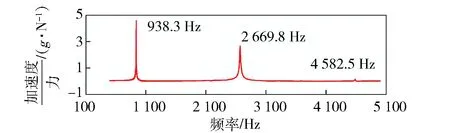
圖3 無螺紋試件前3階頻率響應曲線Fig.3 Frequency response curve of threadless specimen

2.2.2 螺紋連接試件的模態試驗

由于螺紋連接中存在非線性因素的影響，導致模態頻率出現下降。當激勵力較小時，螺紋接觸表現出黏滯特征，隨著激勵力的逐漸增加，螺紋連接非線性因素的影響會逐漸增大，由黏滯特征向微滑移甚至宏滑移過渡。影響螺紋連接接觸特性的因素有很多，例如粗糙度、潤滑情況、預緊力等，為了突出研究主體與核心變量，選擇螺紋預緊狀態作為研究的變量，分別研究螺紋緊連接與松連接兩種連接狀態。因螺紋松、緊連接狀態無法準確量化，為了便于分析，采取了在緊連接螺紋基礎上將螺紋回旋1圈的方式來表征螺紋松連接狀態。采用0.8 N、0.1 N兩種激勵力幅值進行激勵；為了提高測量的精度，對各階頻率進行分段掃頻激勵，激勵頻率分別為100～1 500 Hz、2 000～3 500 Hz、3 500～5 000 Hz，掃頻速度為10 Hz/s. 試驗結果如表1所示。

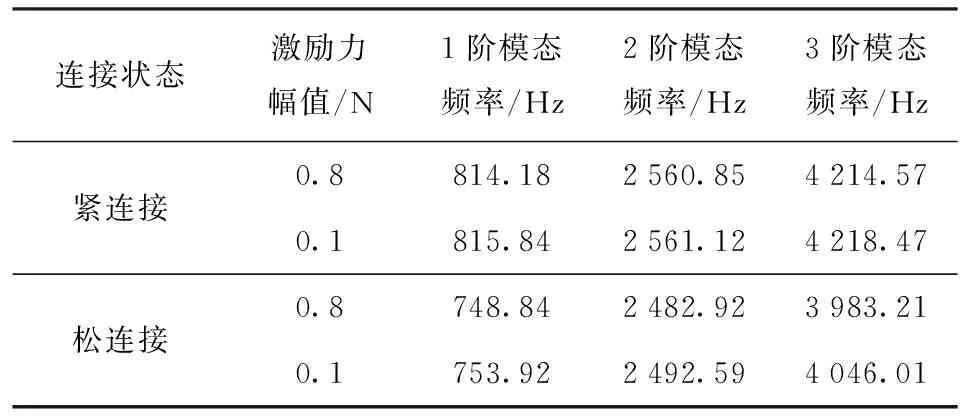
表1 4種工況下試驗獲得的前3階模態頻率

通過表1中的數據對比分析發現，各階模態頻率與無螺紋試件相比出現不同程度的下降，松連接狀態下模態頻率下降的幅度更大，且隨著激勵力幅值從0.1 N增加到0.8 N，緊連接螺紋模態頻率基本上未發生變化，松連接螺紋模態頻率變化較大，表明激勵力的變化未改變緊螺紋的接觸狀態，而使松螺紋的接觸狀態出現了變化。

圖4為試驗與數值仿真獲得的1階頻率響應曲線對比圖。比較無螺紋試件的頻率響應曲線可知，數值仿真獲得的無螺紋試件1階頻率響應曲線與試驗頻率響應曲線形態一致，峰值頻率為948.5 Hz，與試驗值比較誤差為1.09%. 對比無螺紋試件與螺紋試件的頻率響應曲線發現，1階模態頻率從938 Hz分別下降到815 Hz和753 Hz左右，且松連接螺紋模態頻率下降更明顯，表明松連接狀態相比較緊連接狀態受非線性因素的影響更加明顯。最后比較松連接螺紋與緊連接螺紋的頻率響應曲線可得，激勵力的變化會影響螺紋的接觸狀態。隨著激勵力增加,松連接螺紋模態頻率從753.92 Hz下降到748.84 Hz，頻率響應曲線幅值從1.32下降到1.18，分析原因為隨著激勵力的增加，螺紋接觸面狀態已從黏滯狀態轉變為微滑移狀態，摩擦阻尼增大，造成幅值與模態頻率的同時下降；而對于螺紋連接緊密的情況下，隨著激勵力變化，1階模態頻率從815.84 Hz變到814.18 Hz，頻率響應曲線幅值從1.55增加到2.02，與松連接情況表現出完全不一樣的形態，原因為緊連接狀態下螺紋之間的接觸為黏滯狀態，當激勵力幅值增大到0.8 N時也未改變螺紋實際接觸形態。綜上所述，為保證仿真模型與結果的精度，不宜將螺紋接觸面的節點直接進行固連處理，需要根據螺紋接觸的實際情況，準確地表征螺紋的接觸狀態，才能保證仿真模型的精度。

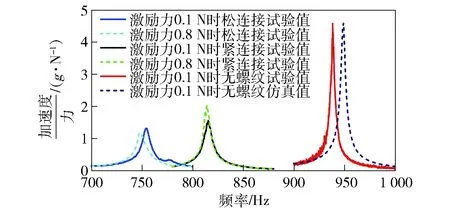
圖4 螺紋結構與無螺紋結構1階頻率響應曲線Fig.4 The first-order frequency response curves of thread and threadless structures

3 螺紋連接薄層單元建模

Shokrollahi等[17]在研究中將組合結構接觸表面分別由法向方向進行擴展定義為接觸影響區域，參考其研究成果，本文根據實際螺紋齒高分別由法向延伸t/2作為螺紋接觸影響區域，如圖5所示，采用厚度為t的薄層單元來模擬螺紋影響區域，薄層單元的長度為內外螺紋結合面長度。根據螺紋的齒高選擇薄層單元的厚度為2 mm，最終仿真模型由3個部分組成：內螺紋管、外螺紋管、薄層單元。薄層單元外徑為38 mm，內徑為34 mm，長度為40 mm. 有限元網格模型如圖6所示。內、外螺紋管與薄層單元均采用8節點實體單元建模，網格單元總數為57 250個。

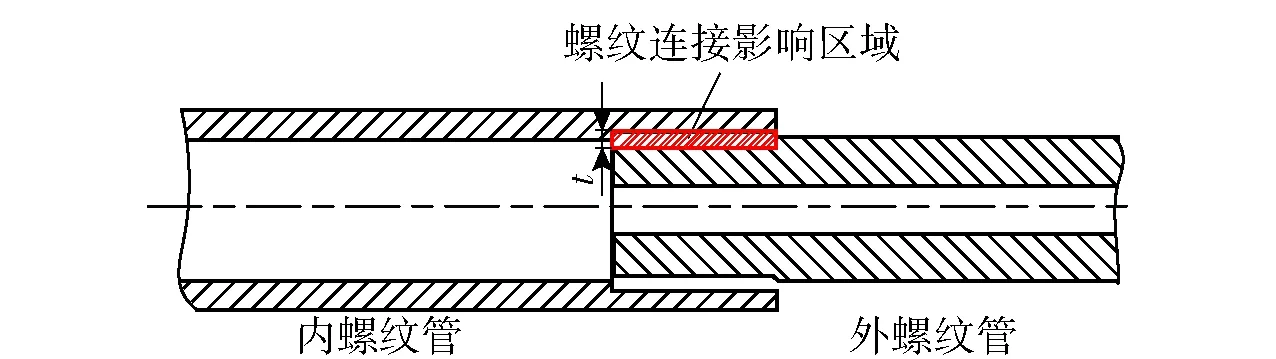
圖5 螺紋連接影響區域示意圖Fig.5 Schematic diagram of joint affected region

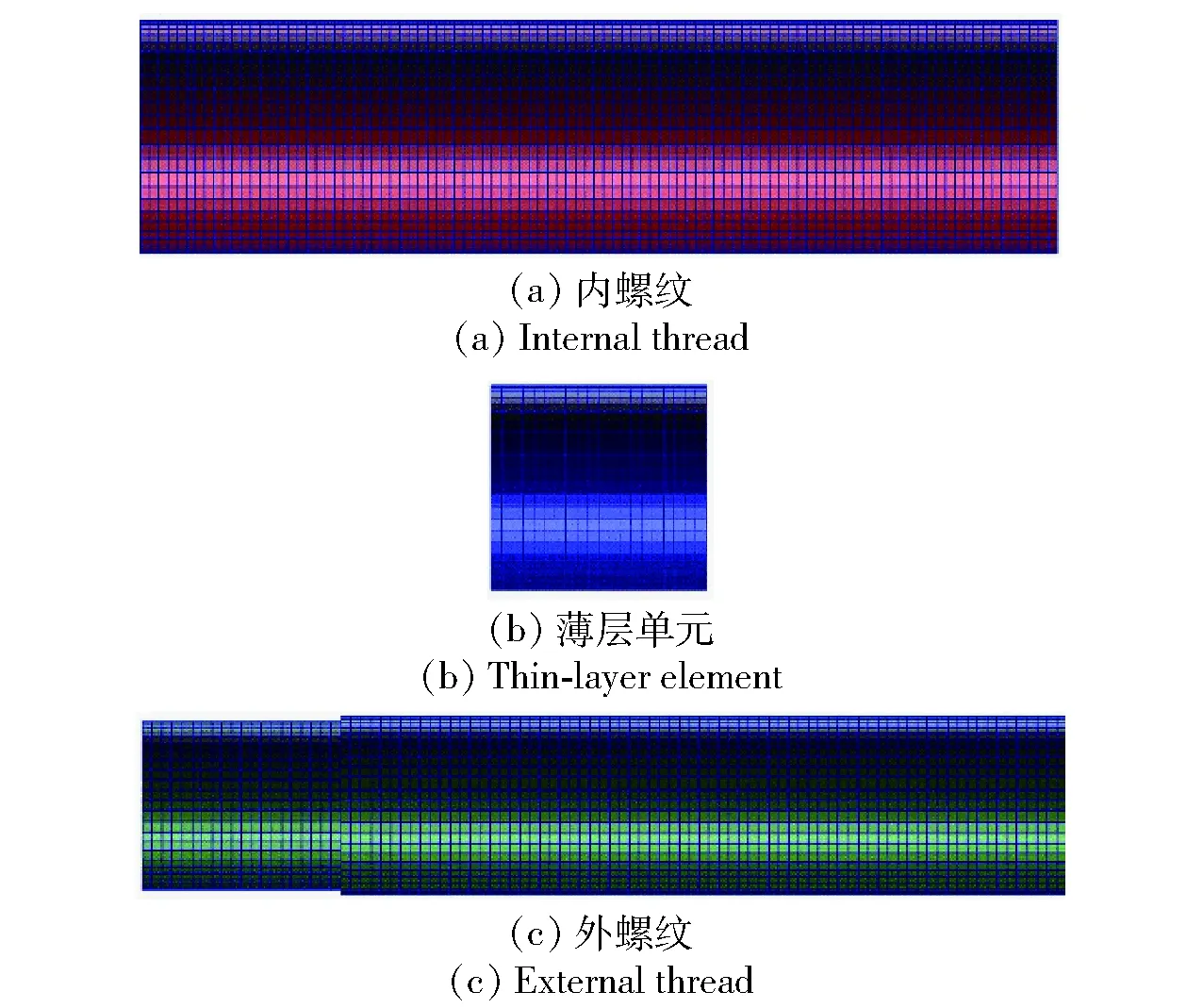
圖6 內、外螺紋管與薄層單元有限元模型Fig.6 Finite element model of internal/external thread and thin-layer element

薄層單元與螺紋管的連接采用MPC技術，MPC連接允許在計算模型不同的自由度之間強加約束[18]，常用于對螺紋連接或螺栓連接等非線性問題的處理[19- 20]。如圖7所示，將內螺紋與薄層單元外表面、外螺紋與薄層單元內表面建立MPC，并選擇內、外螺紋處的節點設置為從節點；薄層單元對應處的節點設置為主節點，約束類型RBE2，如圖8所示，共建立內、外兩層連接，對應的節點處設置為1個MPC，約束總個數為2 100個。通過節點之間約束來進行力的傳遞。

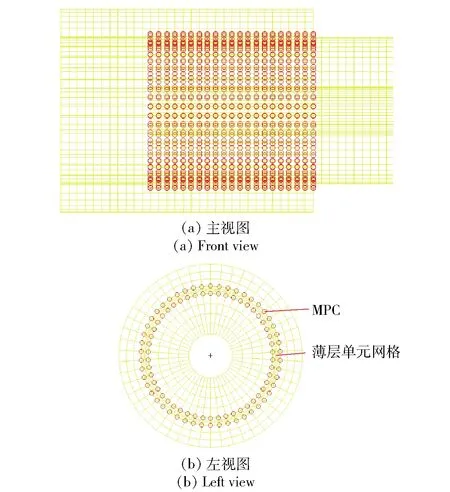
圖7 薄層單元節點MPC約束示意圖Fig.7 MPC constraint diagram of thin-layer element joint

在正式計算之前，需要對材料參數與模型進行驗證，采用Nastran有限元軟件對無螺紋試件進行仿真計算，螺紋管材料為45號鋼，采用線彈性材料模型，材料參數[21]如表2所示。仿真結果如表3所示，仿真計算得出前3階模態頻率相比試驗值偏差分別為1.09%、1.29%、0.21%，結果表明材料參數與材料模型是合理的。

圖8 螺紋有限元模型Fig.8 Finite element model of thread connection

表2 材料參數[21]

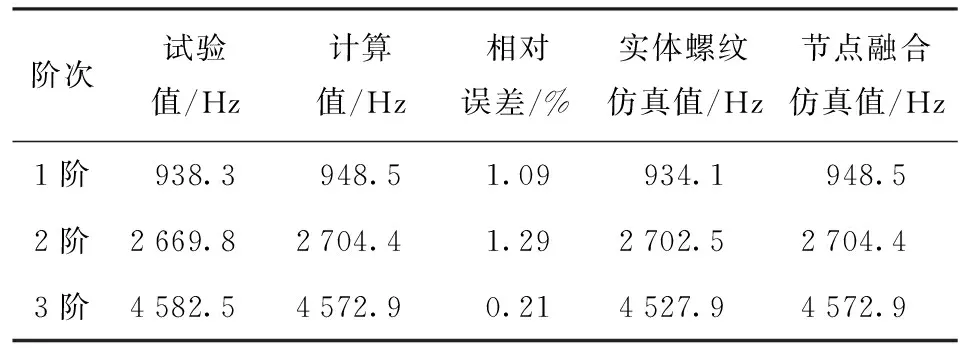
表3 模態頻率仿真與試驗結果

對于螺紋結構，為了簡化分析，常用的方法將接觸面處的節點直接融合，這樣處理相當于將螺紋連接看成整體結構，忽略了螺紋結構，同時也忽略了螺紋連接之間的接觸狀態。為了進行分析對照，建立內、外螺紋管實體螺紋模型(見圖8)，螺紋接觸按照實際尺寸進行建模，為了提高計算效率，采用六面體單元進行網格劃分，螺紋接觸面上的節點進行綁定處理，然后進行模態分析，計算結果如表3所示。對比表3中節點融合與實體螺紋兩種仿真處理方式可知，兩種仿真方式的結果相差不大，說明動力學分析中，對計算結果起主要影響的是接觸之間的非線性因素。

4 薄層單元參數識別

4.1 基于模態頻率薄層單元參數識別

在動力學仿真計算過程中，由于常用的仿真軟件不能識別螺紋的非線性因素，所以對接觸剛度與阻尼等非線性因素不進行考慮，在仿真建模時直接將接觸面的節點融合，這樣與實際的螺紋連接情況相比，會使連接處的剛度增大、阻尼減小，最終導致仿真計算結果偏大。通過在螺紋連接處引入薄層單元來模擬螺紋連接處的接觸剛度與摩擦阻尼，為了準確地表征接觸剛度與摩擦阻尼，需要合理地選擇薄層單元材料參數，采用的方法主要是通過調節薄層單元的材料參數使薄層單元仿真模型的預測值與實際觀察值之間的差值最小，最終獲得的薄層單元材料參數即為最合理的材料參數。采用Nastran設計靈敏度分析模塊進行薄層單元參數識別，選擇薄層單元彈性模量與密度作為設計優化變量，優化目標函數為

(8)

式中：Ci為各階頻率的權重因子；ωFEMi、ωti為模型預測與試驗觀測第i階模態頻率。

Nastran設計靈敏度程序由Muira在1988年提出，是一種迭代線性本征靈敏度方法，基本表達式為

(9)

式中：Δλn為特征值的變化；φn為變換矩陣；ΔK、ΔM分別為剛度與質量的變化。

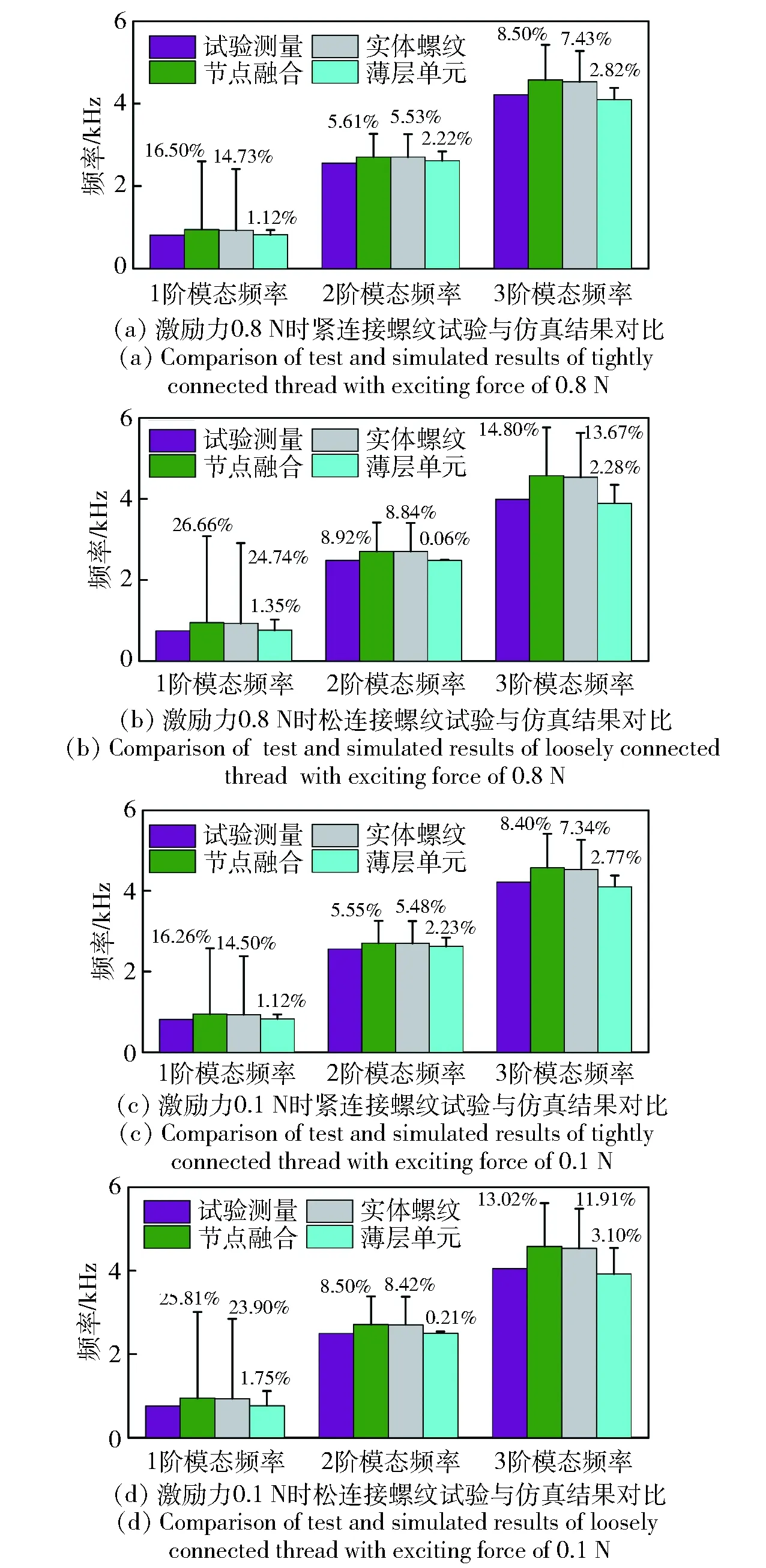
圖9 試驗測量與節點融合、實體螺紋、薄層單元模型3種仿真計算結果對比Fig.9 Comparison of test and simulated results of node merging, solid thread and thin-layer element model

薄層單元采用線彈性材料模型，初始材料參數與螺紋材料一致，彈性模量為211 GPa，密度為7 890 kg/m3. 各階模態頻率的權重因子為1，然后對薄層單元的材料參數進行識別，識別后的薄層單元模型計算結果如圖9所示。對圖9中數據對比發現，采用實體螺紋進行建模，考慮了螺紋的形態，計算誤差相比節點融合誤差要小，但是二者計算結果相差不大。由于這兩種建模方式均未考慮接觸之間的非線性因素，造成計算結果均偏大，都不能很好地對試驗結果進行描述。柱狀圖中誤差棒顯示：在螺紋緊連接狀態，1階模態頻率的仿真值相比較激勵力0.8 N時測量值誤差最大，為16.50%；在螺紋松連接狀態下，1階模態頻率的仿真值相比較激勵力為0.8 N時測量值誤差最大，為26.66%. 采用薄層單元的仿真計算方式，緊連接狀態下的最大誤差從16.50%下降到1.12%；松連接狀態下的最大誤差從26.66%下降到1.35%. 說明采用薄層單元可以準確地模擬螺紋之間的接觸狀態，且無論螺紋是處在緊連接狀態還是松連接狀態，薄層單元仿真計算結果與試驗結果較一致。

為了研究模態頻率ω關于設計變量的靈敏度，對目標(8)式進行靈敏度分析計算。由于4組試驗數據性質一致，選取激勵力為0.8 N、緊連接螺紋的試驗數據為分析對象，當設計變量僅為E或ρ，以及同時為E與ρ3種情況時，計算結果如表4所示。由表4可知，相比彈性模量，模態頻率優化目標對密度變化更敏感，采用密度作為優化變量迭代4次后收斂，而僅采用彈性模量作為優化變量需要9次才能收斂。

表4 模態頻率靈敏度分析結果

4.2 基于頻率響應曲線薄層單元參數識別

螺紋接觸之間存在接觸剛度與摩擦阻尼，會使頻率響應曲線尖峰頻率出現偏移，尖峰處的幅值發生變化。如試驗部分測得的頻率響應曲線顯示，由于接觸剛度與摩擦阻尼的影響，不同連接狀態、不同的激勵力幅值，試驗測得的頻率響應曲線會表現出不一樣的形態。在仿真分析的過程中，如果不對螺紋接觸狀態進行考慮，將會引起很大的誤差。利用薄層單元來模擬接觸剛度與摩擦阻尼，使模型頻率響應曲線預測的結果與試驗結果一致。為了準確地對接觸狀態進行模擬，需要對薄層單元的材料參數進行識別，采用的方法是通過調整薄層單元的材料參數使頻率響應曲線各個頻率點處幅值與試驗觀察獲得的幅值一致，最后獲得薄層單元的參數即為識別得到的參數。參數識別的目標函數為

(10)

式中：n為所取頻率點數目；aFEM(ωi)為預測頻率響應曲線頻率點ωi處的幅值；at(ωi)為試驗觀察頻率響應曲線頻率點ωi處的幅值。

利用Nastran結構動力學優化模塊來對薄層單元的參數進行識別，其優化過程在頻率響應函數靈敏度分析的基礎上進行，頻率響應函數對變量x靈敏度分析表達式為

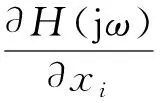
(11)

式中：m、c、k分別為廣義質量矩陣、廣義阻尼矩陣、廣義剛度矩陣。

第3階頻率響應曲線的幅值與第1階、第2階相比可以忽略不計，所以只對第1階與第2階頻率響應曲線進行考慮，將第1階頻率響應曲線作為目標函數(10)式中試驗觀察值，獲取薄層單元參數，然后利用第2階頻率響應曲線對識別的材料參數進行驗證。薄層單元初始材料參數與螺紋結構一致，激勵方式、幅值、作用位置以及響應點位置與試驗保持一致，選擇薄層單元的密度與彈性模量為設計變量，1階模態頻率為約束變量，選擇1階模態頻率附近一系列頻率點組成目標函數。為提高計算效率，在構造目標函數的時候，在模態頻率尖峰處間隔可以取得小一些，而在遠離尖峰處頻率間隔可以適當增大。

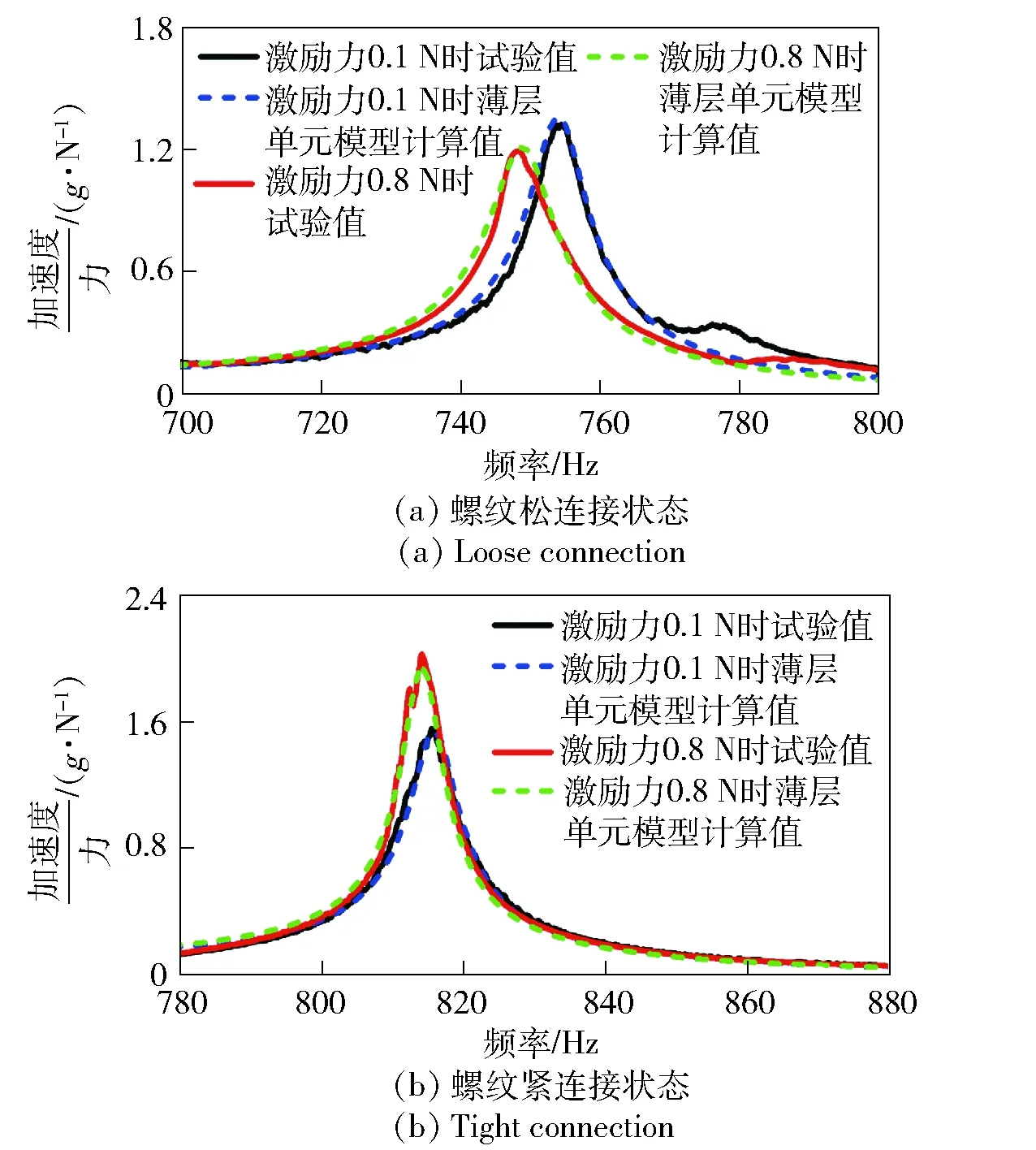
圖10 試驗與薄層單元模型的1階頻率響應曲線Fig.10 The first-order frequency response curves of experiment and thin-layer element model

緊連接螺紋的設計變量經過20次迭代后達到穩定，松連接螺紋的設計變量經過25次迭代后達到穩定。摩擦阻尼的控制主要通過調節模態阻尼參數，當設計變量逐漸收斂，達到穩定時，此時目標函數取得最小值，薄層單元參數識別結束。經過參數識別后，薄層單元模型計算得到1階頻率響應曲線與試驗得出的頻率響應曲線對比如圖10所示。模型計算得到的頻率響應曲線與試驗頻率響應曲線各頻率點處吻合較好，整體上基本一致，表明參數識別后薄層單元可以準確地模擬螺紋接觸面之間的接觸剛度與摩擦阻尼，能夠準確地描述試驗現象。

利用2階頻率響應曲線對識別后的薄層單元材料參數進行驗證。識別后的薄層單元參數計算出的2階頻率響應曲線與試驗觀測到的2階頻率響應曲線如圖11所示，圖中試驗獲得的2階頻率響應曲線左側會出現突起，分析原因可能是由于外界干擾所導致。模型預測的2階頻率響應曲線與試驗獲得的2階頻率響應曲線尖峰處形態基本上一致，只是峰值頻率有小幅度的偏移，螺紋松連接狀態下，薄層單元模型計算2階模態頻率為2 502.12 Hz、2 507.93 Hz，相比試驗結果誤差分別為0.78%、0.64%. 螺紋緊連接狀態下，模型預測得到的2階模態頻率分別為2 571.11 Hz、2 573.32 Hz. 相比試驗值誤差分別為0.43%、0.42%，由于2階模態頻率較大，頻率響應曲線的偏移量相比真值可以忽略不計，表明經過識別后的材料參數是準確的，可以準確地表征螺紋連接接觸狀態。

圖11 試驗與薄層單元模型2階頻率響應曲線Fig.11 The second-order frequency response curves of experiment and thin-layer element model

為研究頻率響應曲線目標函數f關于設計變量的靈敏度，對目標(10)式進行靈敏度分析計算，同樣選取激勵力為0.8 N，緊連接螺紋的試驗數據為分析對象，由于設計變量僅為E或ρ時，無法達到優化的目的，因此僅選擇E與ρ同時作為設計變量的情況進行計算，結果見表5所示。可知，相比彈性模量，頻率響應曲線優化目標對密度變化更敏感，可以將密度的變化作為粗調方式，而將彈性模量變化作為微調方式。

表5 頻率響應曲線靈敏度分析結果

4.3 薄層單元厚度對識別精度的影響規律研究

當采用薄層單元模擬螺紋接觸的剛度與摩擦阻尼時，薄層單元的厚度將影響參數的識別精度，下面將對這一問題進行研究。

圖12為螺紋連接薄層單元示意圖，F為螺紋連接所受的軸力，τ為薄層單元受軸力F后產生的剪切應力,剪切應力可以表示為

(12)

式中：Gs為剪切模量；γ為剪切角；A為接觸面積；u為軸向位移。

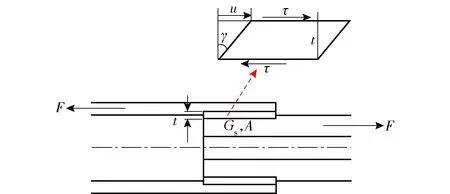
圖12 螺紋連接薄層單元示意圖Fig.12 Schematic diagram of thread-connected thin-layer element

對(12)式進行變換，可得

(13)

式中：K為螺紋連接的軸向剛度。

根據(13)式薄層單元的剪切模量Gs可以表示為

(14)

根據(14)式可知，薄層單元的厚度t與剪切模量Gs呈正比，說明薄層單元厚度的選擇會對剪切模量的識別存在影響。定義薄層單元厚度的一半t/2與螺紋齒高H比值為薄層單元無量綱厚度，選取薄層單元無量綱厚度t/(2H)分別為0.46、0.92、1.39、1.85，然后分別對4種厚度的薄層單元進行材料參數的識別，并以(8)式、(10)式兩個目標函數計算值作為評價標準。如果收斂后目標函數最小，說明參數的識別效果最好，采用松連接條件下，激勵力0.1 N的試驗數據作為目標表達式里面的觀察數據，結果如圖13所示。根據圖13中的數據比較分析可得：薄層單元的厚度不同，模態頻率目標函數相差不大，但頻率響應曲線目標函數有較大的差別；當薄層單元無量綱厚度為0.92時，目標函數最小，采用此厚度的薄層單元計算結果準確度最高。綜上所述，可以將兩倍的齒高(2H)作為薄層單元建模的參考，但是為了建模的方便，一般在兩倍的齒高周圍取整數值作為建模的依據。

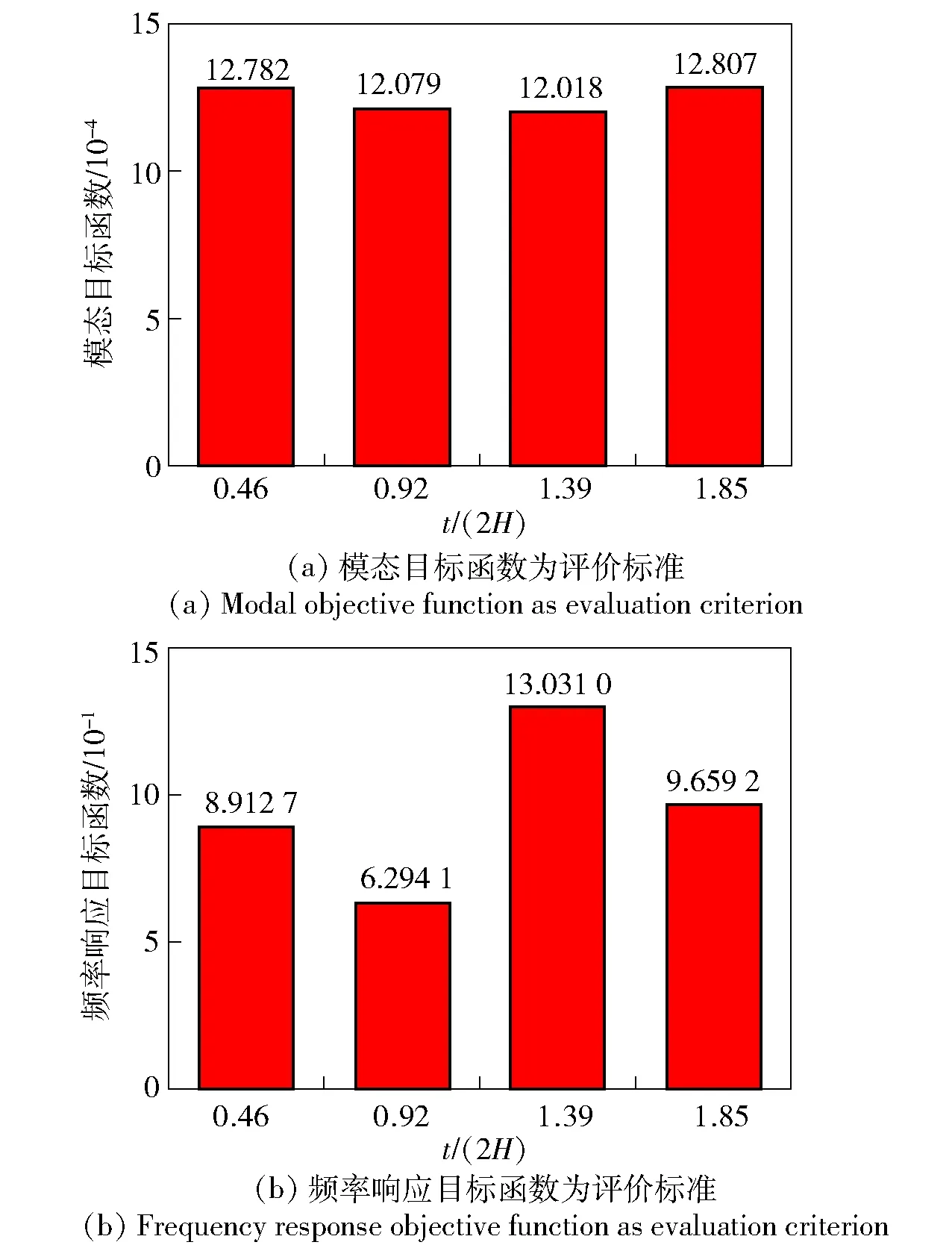
圖13 不同薄層單元厚度目標函數值對比Fig.13 Comparison of objective function values of thin-layer elements with different thicknesses

5 彈體與引信螺紋連接薄層單元建模研究

侵徹彈體與引信體的連接形式為螺紋連接，如圖14所示。螺紋型號為M42×2-6H/6g-33，螺距為2 mm，旋合長度為33 mm. 采用薄層單元模擬彈體與引信系統螺紋連接，有限元模型如圖15所示，有限元模型由3部分組成：彈體、引信體、薄層單元。其中薄層單元厚度為2 mm，長度為33 mm，均采用六面體網格進行劃分，且在螺紋連接處網格適當加密。薄層單元與彈體、引信體之間的節點連接采用MPC方式。彈體與引信材料均為高強鋼30CrMnSiNi2A，材料參數如表6所示，薄層單元初始材料參數與彈體保持一致，采用線彈性材料模型進行表征。在薄層單元參數識別之前需要對彈體與引信系統進行模態試驗，試驗結果如表7中所示。根據模態試驗的測量結果，利用目標表達式(8)式對薄層單元的參數進行識別，然后將識別后的材料參數傳遞入薄層單元模型中，最終計算結果如表7所示。

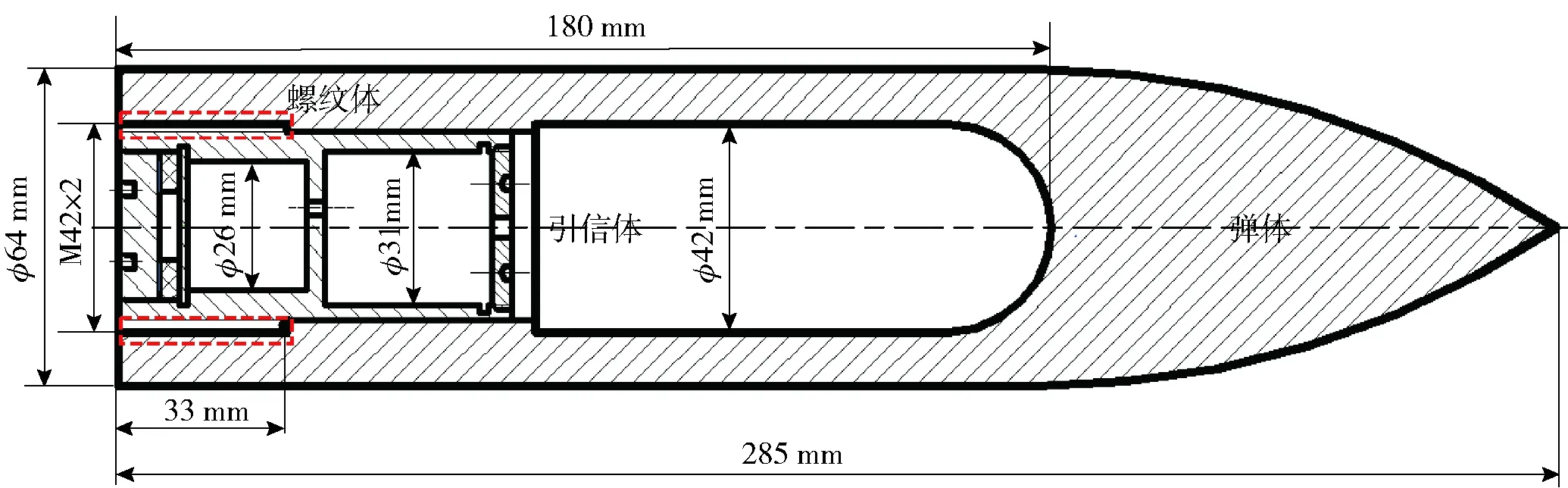
圖14 彈體與引信螺紋連接Fig.14 Thread connection of projectile-fuze system

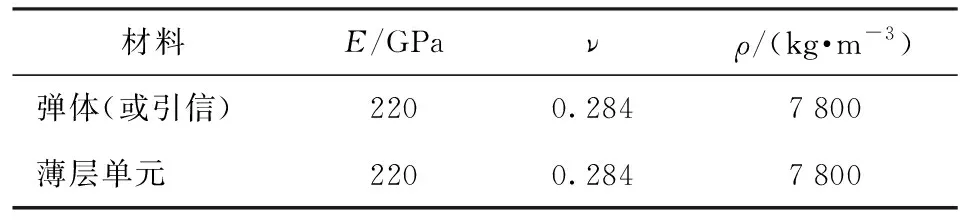
表6 材料參數

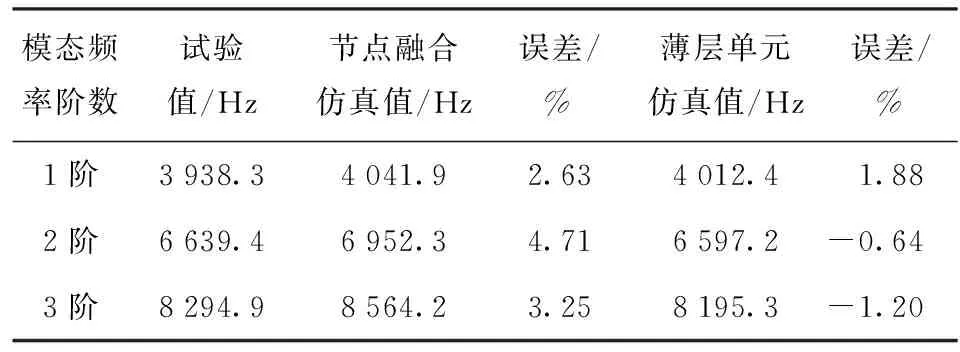
表7 彈體與引信系統試驗與仿真結果對比

由表5中的數據對比發現，采用節點融合模型的計算結果與試驗結果進行比較，誤差分別為2.63%、4.71%、3.25%，采用薄層單元模型進行計算，誤差下降到1.88%、-0.64%、-1.20%，表明在彈體與引信系統動力學分析過程中，采用薄層單元的建模方式可以有效地提高仿真模型的計算精度。

6 結論

螺紋連接接觸剛度與摩擦阻尼等非線性因素對組合部件的振動響應有重要的影響。為了提高螺紋連接構件仿真模型的計算精度，需要準確地表征螺紋連接的接觸狀態，本文嘗試采用薄層單元對螺紋接觸狀態進行模擬，并以模態試驗的數據作為觀測值，結合Nastran優化設計模塊，對薄層單元的材料參數進行識別。結果表明無論螺紋連接處在黏滯、微滑移、宏滑移何種接觸狀態，參數識別后的薄層單元模型均可以較好地表征螺紋接觸狀態。得出以下主要結論：

1) 對于螺紋管結構，薄層單元建模的計算結果與傳統建模方式進行比較，模態頻率最大仿真誤差從26.66%下降到1.35%. 將其應用于彈引螺紋連接結構中，模態頻率最大仿真誤差從4.71%下降到-0.64%，表明薄層單元模型可以有效地提高仿真計算精度。

2) 建立了基于試驗結果對薄層單元材料參數識別的方法，識別后的薄層單元模型可以準確、合理地描述試驗現象。

3) 薄層單元厚度選擇對材料參數的識別精度有重要的影響。當薄層單元厚度與兩倍的齒高相當時，參數的識別精度最高。