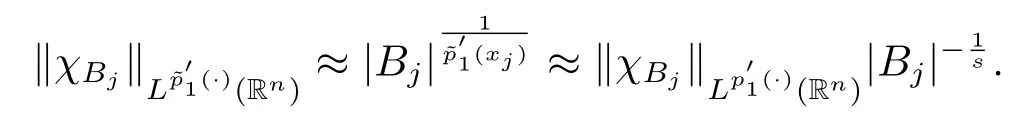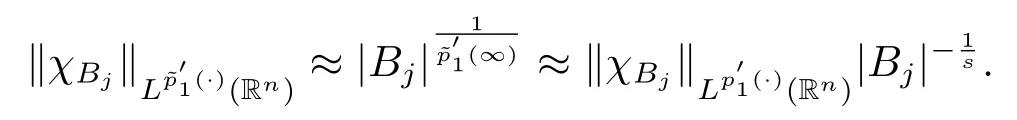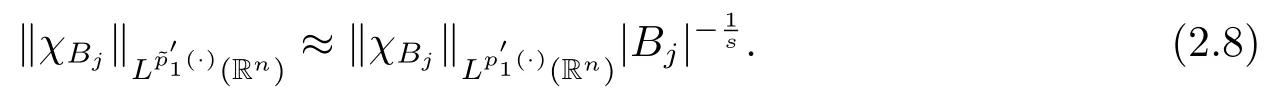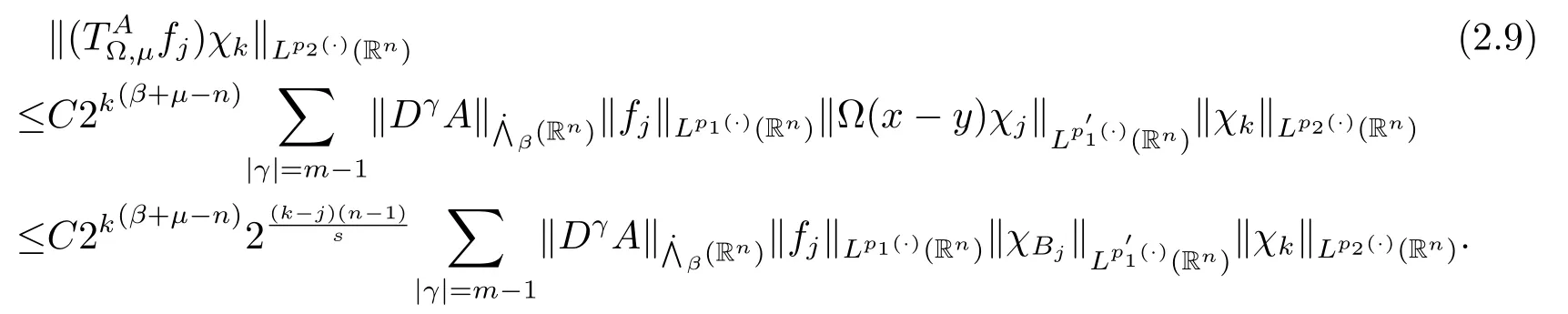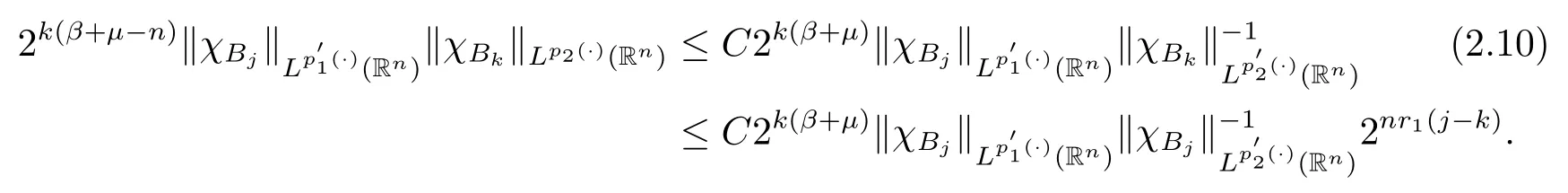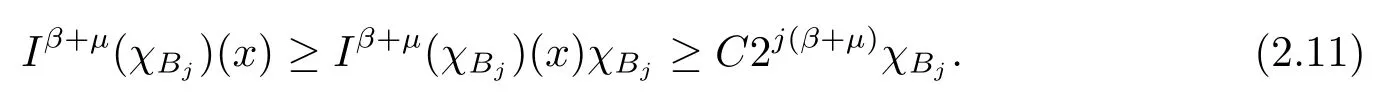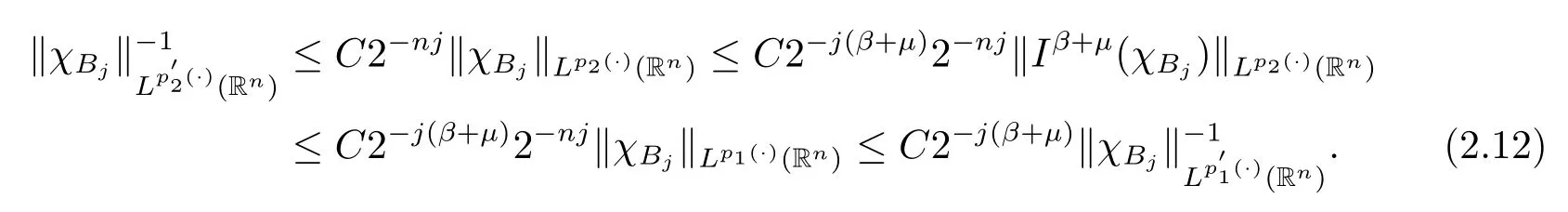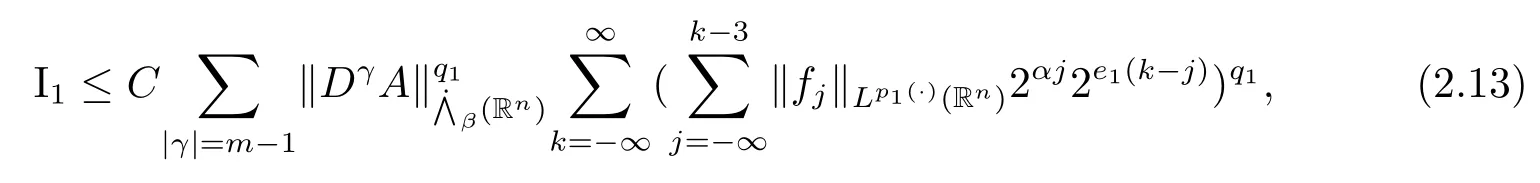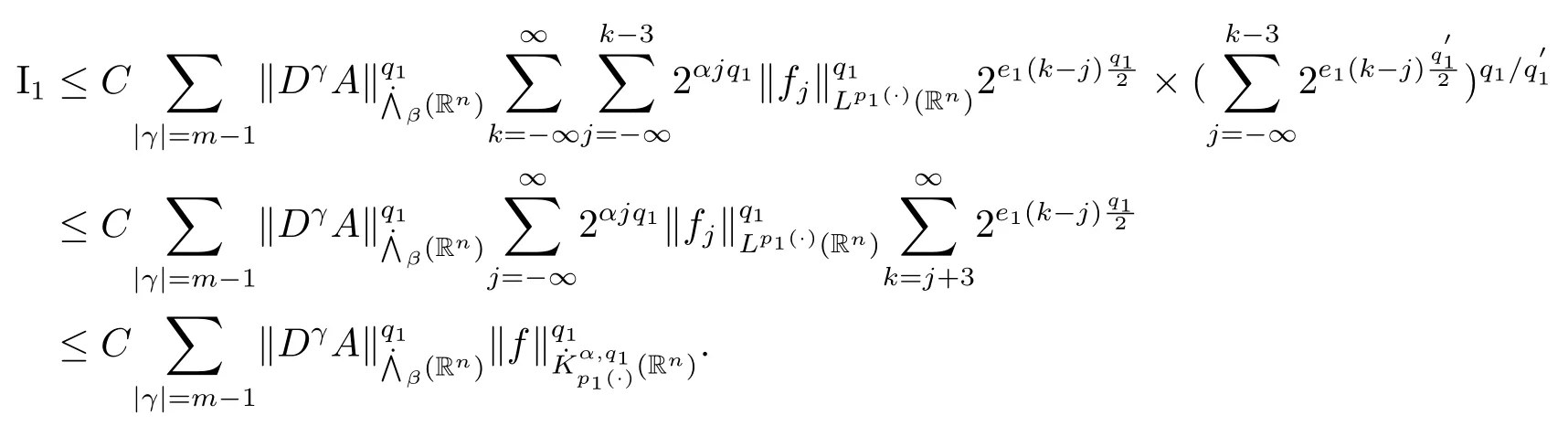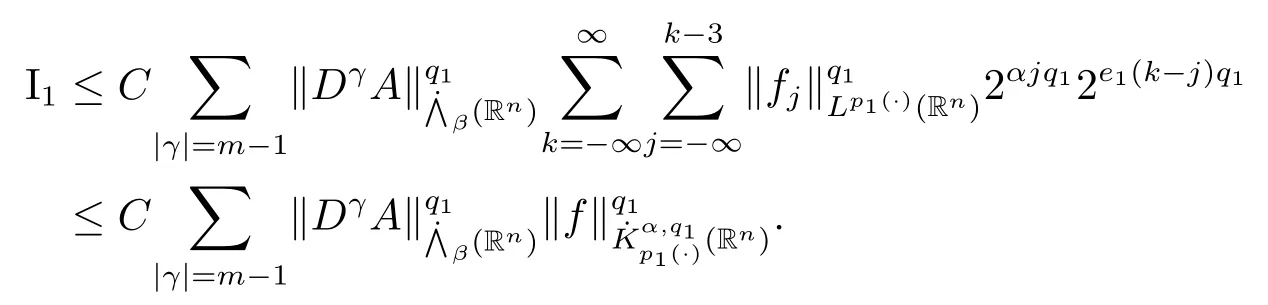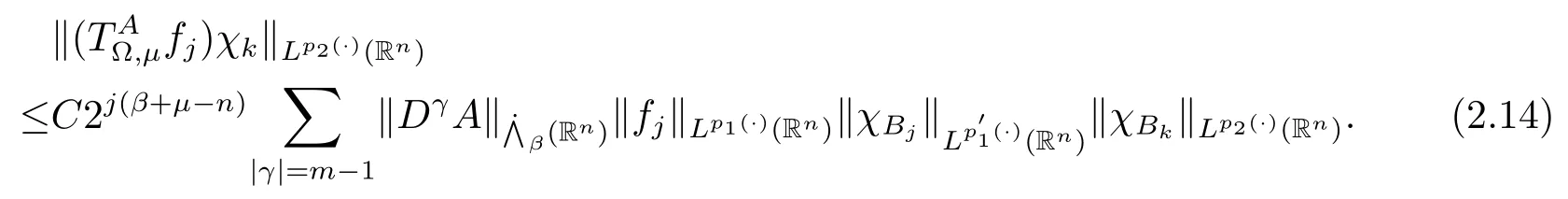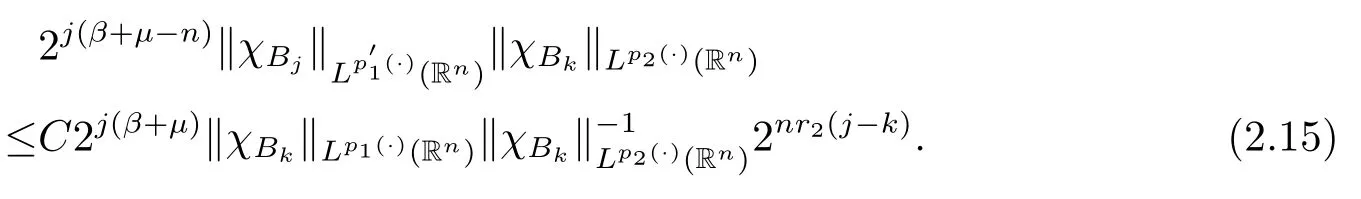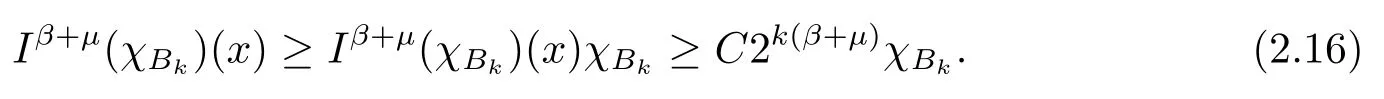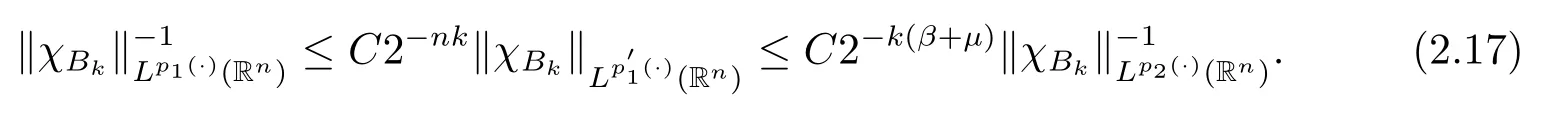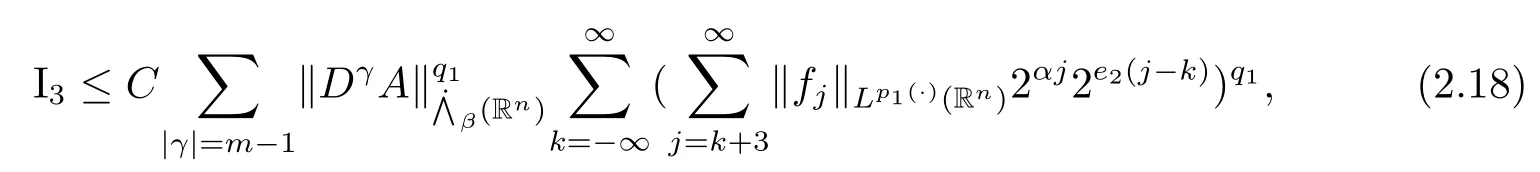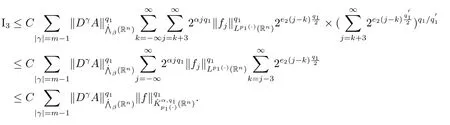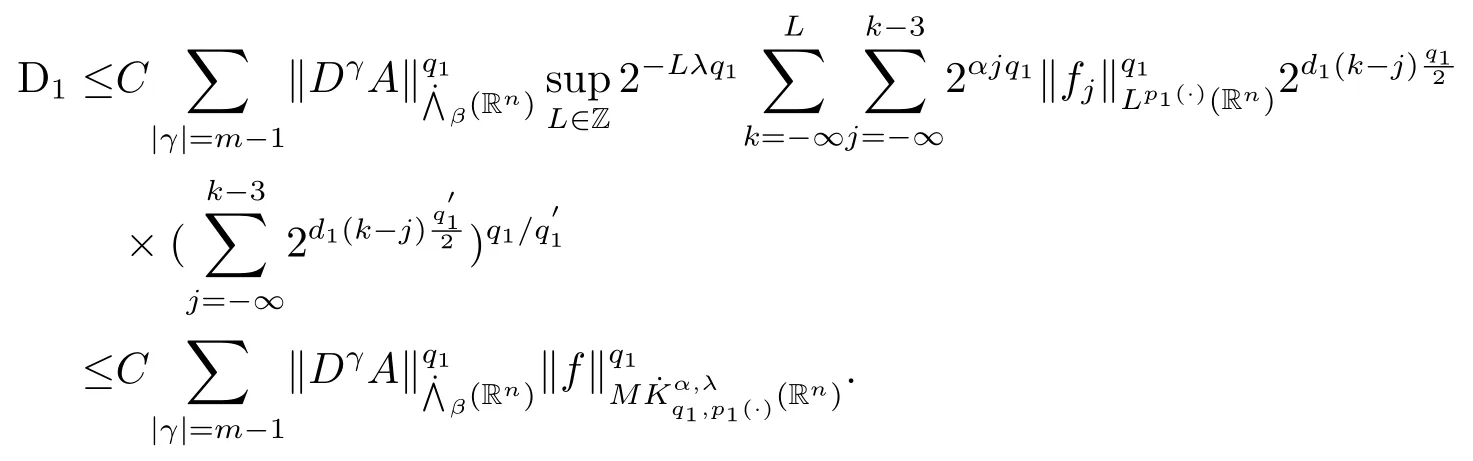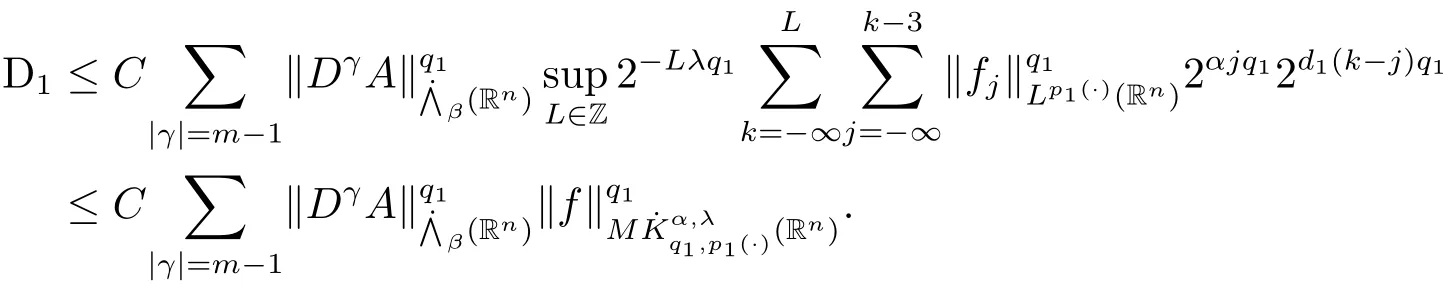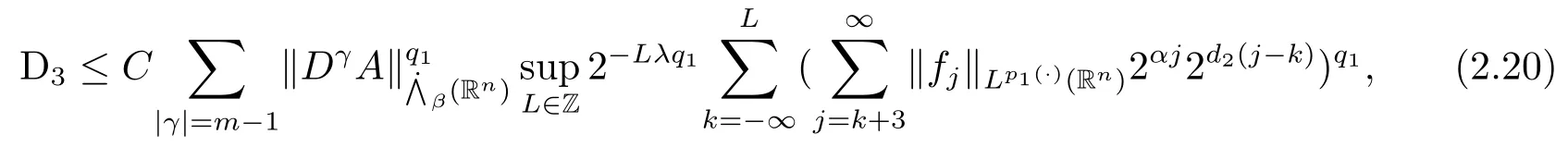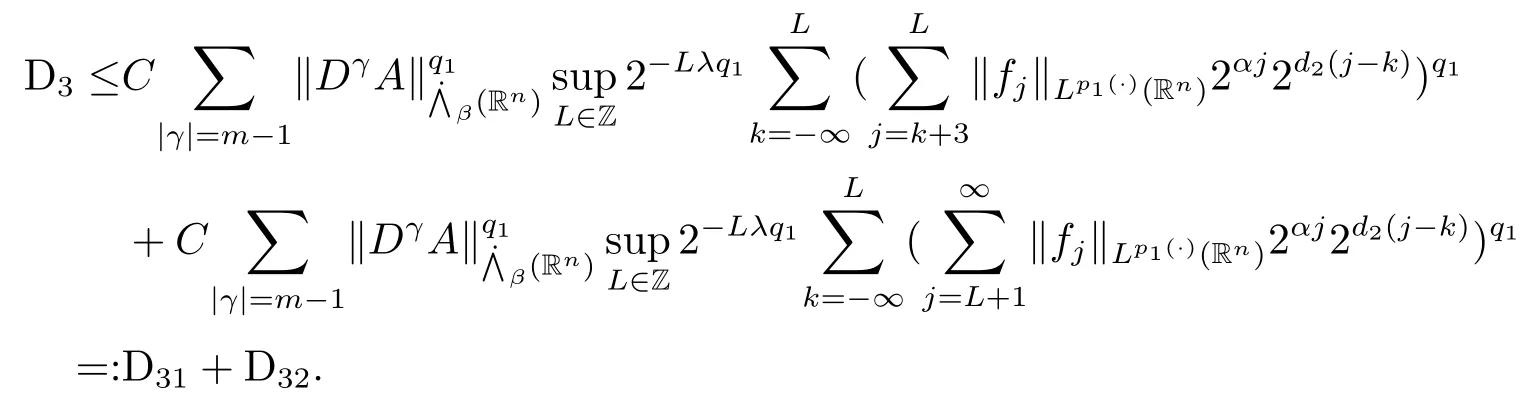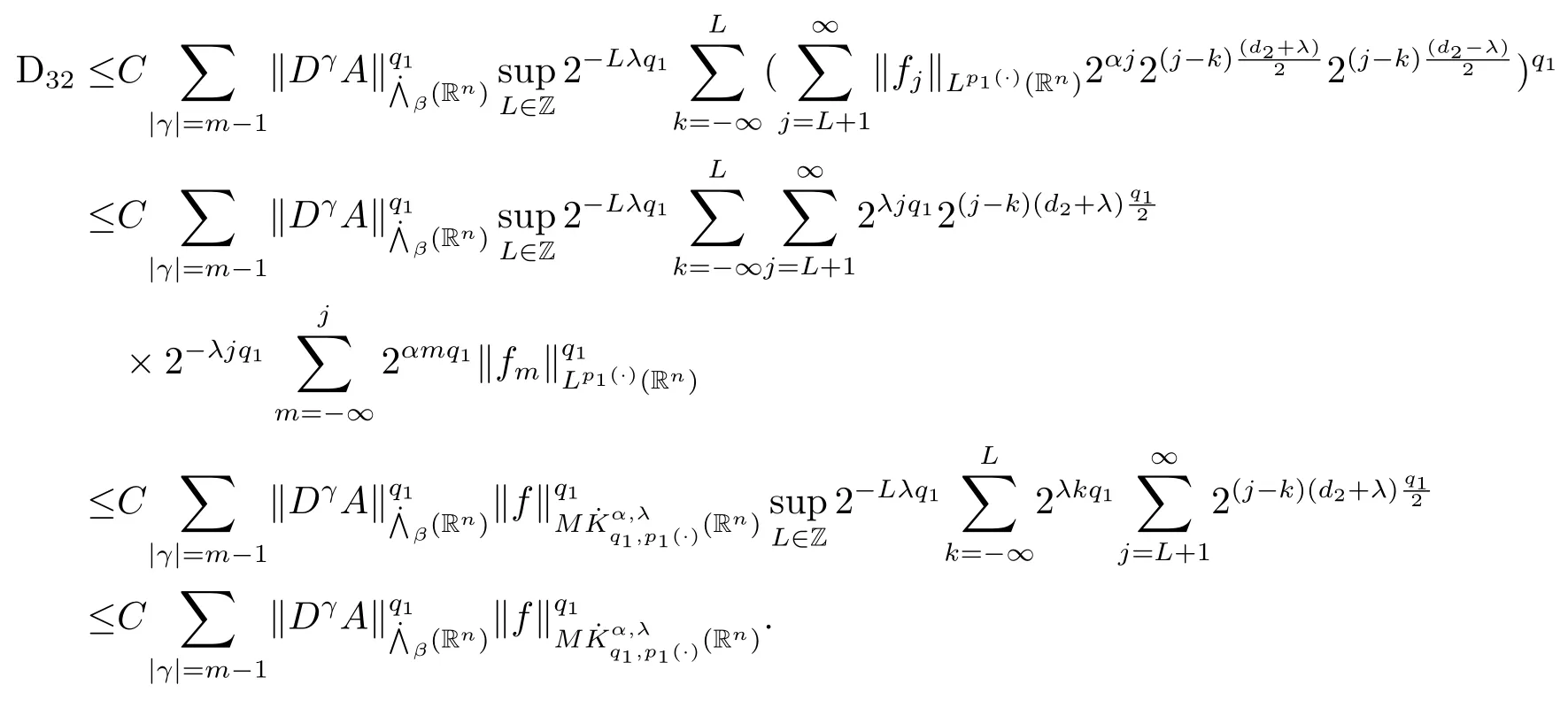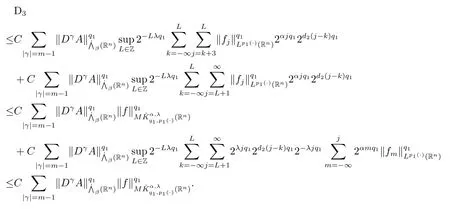多線性分數次積分及其極大算子在變指標Herz空間上的有界性
殷露露,張 婧
(伊犁師范大學數學與統計學院,新疆 伊寧 835000)
1 引言
設0<α

當μ=0時,T?,μ與二階變系數橢圓偏微分方程有著非常密切的聯系.1995年,Caldon與Zygmund證明了該算子在變指標Lebesgue空間Lp(·)(Rn)上有界.隨后,又有很多學者對其進行了進一步的研究[1?3].
令γ=(γ1,γ2,···,γn),并且γi(i=1,2,···,n)是非負整數,記且
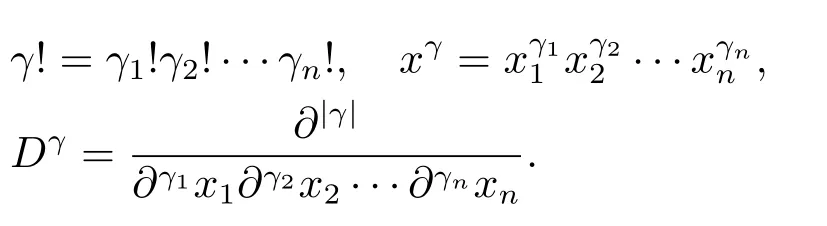
令A(x)是定義在Rn上的函數,Rm(A;x,y)表示定義在Rn上且m?1階可導的函數A(x)在點x關于y的m階Taylor展開式的余項,即
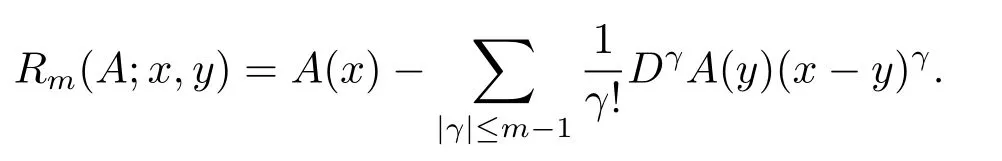
在2001年,丁勇[4]引入了如下一類帶粗糙核的多線性分數次積分算子
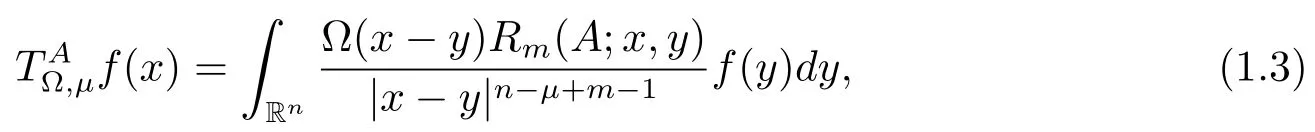
與之相應的分數次極大算子的定義為
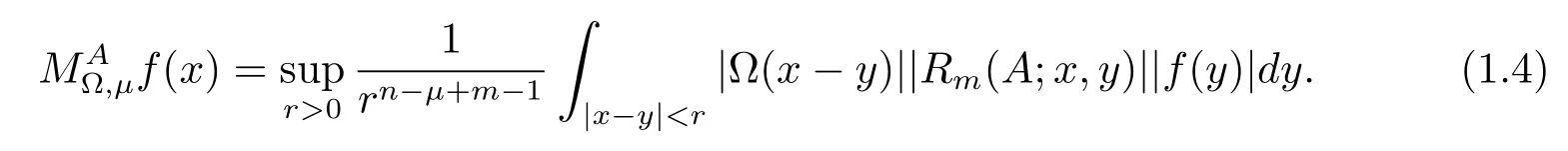
顯然,當m=0時,即為交換子[A,T?,μ].當m≥1時,即為上述交換子的非退化推廣.丁勇[4]證明了當DγA∈Lr(Rn)(1≤r<∞,|γ|=m?1)時,該算子在加權Lebesgue空間上有界;Wu和Yang[5]證明了當DγA∈BMO(Rn)(|γ|=m?1)時,該算子在Lebesgue空間上有界.
另一方面,在1995年,Paluszynski[6]給出了由Riesz位勢算子以及Lipschitz函數生成的廣義交換子,即多線性分數次積分算子,并給出了Besov空間的一些刻畫.在Paluszynski[6]的啟發下,Lu和Zhang[7]證明了當時,在Lebesgue空間上有界.當β>0,齊次Lipschitz空間的定義為
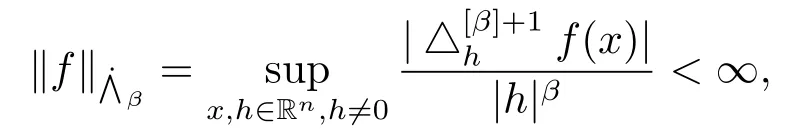
若1≤q<∞,等價范數為
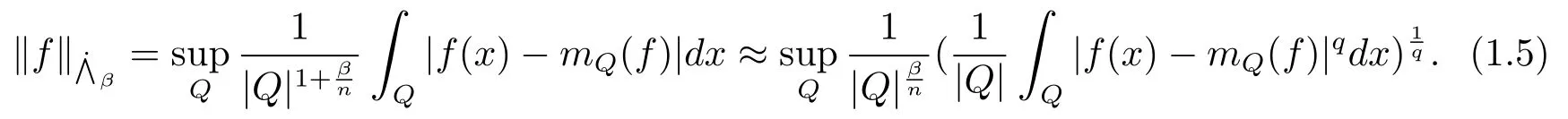
上述都是在一些經典函數空間上的結果,隨著科學的發展,很多非線性的問題隨之而來.這時經典函數空間出現了一定的局限性,例如它對非標準增長條件下的非線性問題已經失去了效用.在這類非線性問題的研究過程中,學者越來越多的關注由經典函數空間到變指標函數空間.
令p(·):Rn?→[1,∞)上的可測函數.記變指標Lebesgue空間Lp(·)(Rn)為存在某個λ>0使得
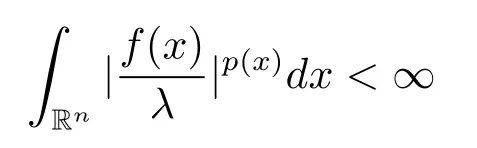
成立的Rn上的可測函數f全體.變指標Lebesgue空間Lp(·)(Rn)是一個Banach空間,其范數定義為記
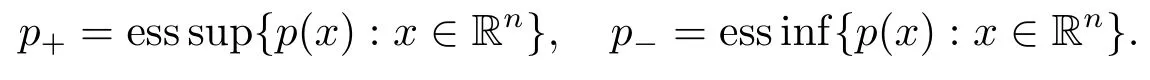
用這個符號定義一族變指標
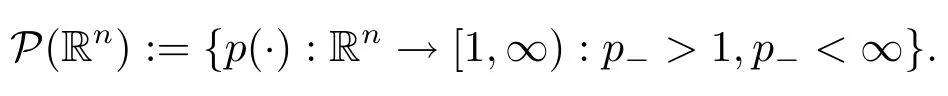
p0(·)是p(·)的共軛指標且
變指標空間與經典函數空間有很大的不同,主要是變指標函數空間已經失去了平移不變性,這一區別導致許多在經典空間中成立的性質在變指標空間中不再成立.隨后一些學者發現只要證明Hardy-Littlewood極大算子M在Lp(·)(Rn)上有界,則相應的的經典調和分析和函數空間理論中的許多結論可以在相應的變指標函數空間中成立.
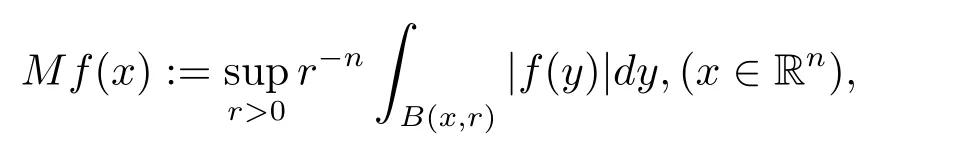
其中B(x,r):={y∈Rn:|x?y| 可以得到p(·)∈B(Rn).則Hardy-Littlewood極大算子M在Lp(·)(Rn)上有界. 在變指標Lebesgue空間Lp(·)(Rn)中,有以下幾個重要的命題. 命題 1.1[8]若p(·),p0(·)∈B(Rn),存在0 其中S是Rn中所有的球B的可測子集. 命題1.2[8]若p(·)∈B(Rn),存在常數C>0,使得Rn中所有的球B滿足 命題1.3[9]若p(·)∈P(Rn),q>p+且,則 命題 1.4[10]令p(·)∈P(Rn)滿足(1.6)和(1.7)式,則有 對于所有的方體(球體)Q?Rn,其中 命題1.5[11]若p(·)∈P(Rn),任意的f∈Lp(·)(Rn),則fg在Rn上可積并且 由命題1.4,當|Bj|≤2n且xj∈Bj,有 通過對關鍵成功領域進行解析與細化,明確了每個關鍵成功領域包含的內容、最主要因素、達成每一個成功領域的標準。如質量安全的關鍵績效要素為醫療質量和醫療安全,運營管理為資產效益、成本控制和管理運營,創新發展為學科人才、新醫療新技術、教學成果、科學研究。 當|Bj|≥1,有 故有 聯立(2.6)–(2.8)式可得 運用命題1.2和(1.1)式可得 另一方面,由分數次積分Iβ+μ可以得到 聯立 (2.9)–(2.12)式可知 情形1若1 情形2若0 最后估計I3,對于任意的j,k∈Z且j≥k+3,類似于(2.9)式的估計,可以得到 運用命題1.2和(1.8)式,類似于(2.10)式的估計可得 另一方面,由分數次積分Iβ+μ可以知道 類似于(2.11)式的估計,可以得到 聯立(2.14)–(2.18)式可得 其中e2:=β+μ+nr2?α<0.為了繼續估計(2.18)式,考慮以下這兩種情形1 情形1若1 情形2若0 這樣就完成了定理1.2的證明.接下來證明定理1.3. 定理1.3的證明令記fj:=fχj(j∈Z),則用(2.1)式可得 首先估計D2,當時,由定理1.1中的有界性可知 類似于定理1.2中I1的估計方法,可得 情形1若1 情形2若0 最后估計D3, 其中d2:=β+μ+nr2?α<0.為了繼續估計(2.20)式,考慮以下這兩種情形1 情形1若1 對于D31,運用Hlder不等式,得到 對于D32,由已知條件d2+λ<0和Hlder不等式,可得 情形2若0 這樣就完成了定理1.3的證明.定理1.4的證明與上述證明類似.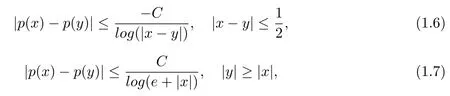
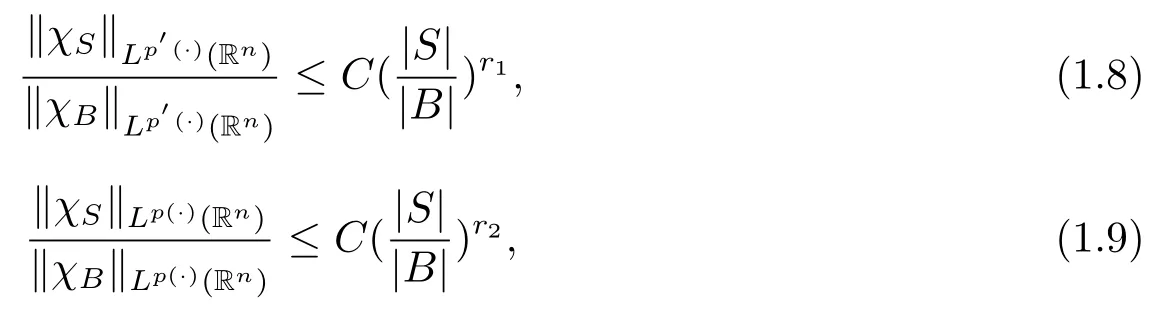
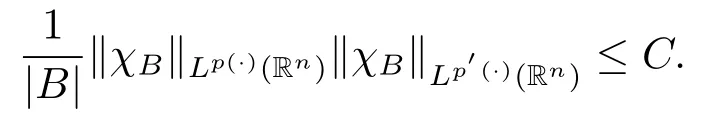
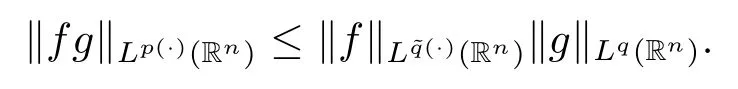
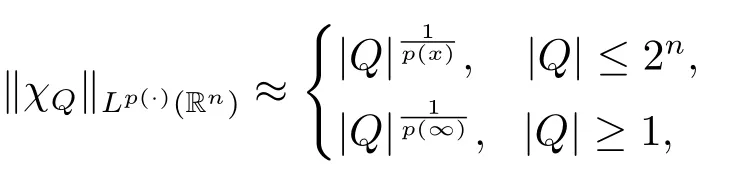
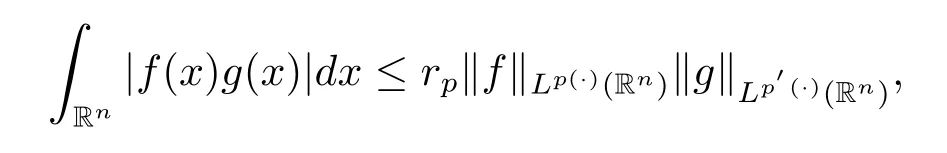


2 主要引理和定理證明