有窮平坦維數的同調轉換刻畫

熊濤

(西華師范大學數學與信息學院,四川南充 637002)

1 引言

本文規定,R恒指有單位元的交換環.對R-模N,fdRN(resp.pdRN)代表N的平坦(resp.投射)維數.用Fn表示平坦維數不超過n的R-模簇,用w.gl.dim(R)表示R的弱整體維數.對于未解釋的概念和符號,參考文獻[1,2].

文獻[3]引入的FFD(R)維數受到了廣泛關注.例如,文獻[4,推論5.3]表明,一個Noether環R,總有FFD(R)≤dim(R)≤FFD(R)+1成立,這里dim(R)是R的Krull維數;特別地,如果R是局部環,則FFD(R)=dim(R)當且僅當R是Cohen-Macaulay環.

稱R是chain環是指其理想按包含關系所構成的格是全序的,R稱為arithmetical是指對R的每個極大理想m,Rm是chain環.R稱為半凝聚環是指對任何一對內射模E,F,HomR(E,F)是某個平坦模的子模.文獻[5,定理1]證明了對每個交換的arithmetical環R,總有FFD(R)≤2成立.更確切地說,當R為局部IF(locally IF)環時,FFD(R)=0成立;當R是局部半凝聚(locally semicoherent)環但不是局部IF環時,都有FFD(R)=1,這里環R稱為IF環是指每個內射R-模是平坦模,(見文獻[6]).文獻[5,定理2]證明了當R既是IF環又是chain環時,則FFD(R)=0;當R是非半凝聚的chain環時,都有FFD(R)=2.

在經典同調理論中,環R的整體維數是所有模的投射維數(或者內射維數)的上確界;弱整體維數w.gl.dim(R)是模的平坦維數的上確界.在相對同調理論中,環R的Gorenstein整體維數也是所有模的Gorenstein投射維數的上確界,或者Gorenstein內射維數的上確界;Gorenstein弱整體維數是所有模的Gorenstein平坦維數的上確界.

然而,環的有窮平坦維數FFD(R)不是像經典同調理論和相對同調理論那樣,建立在整個R-模范疇上,而是建立在平坦維數有限的子范疇上.對任給一個模M,在判定其平坦維數是否有限時,存在技術上的困難.本文借助文獻[7]中提出的n-無撓模,建立了整個R-模范疇上的n-無撓分解,任何模的n-無撓維數,以及環R的n-無撓弱整體維數w.T Fn.D(R).證明了環R有FFD(R)≤n當且僅當w.T Fn+1.D(R)≤n,通過這個結果,將對FFD(R)的計算轉換成了對w.T Fn+1.D(R)的計算.

2 環的有窮平坦維數

定義2.1對R-模M,用tfndRM表示這樣的最小整數m≥0,存在正合列0→Dm→Dm?1→···→D1→D0→M→0,這里每個Di是n-無撓模.如果這樣的整數m不存在,則記tfndRM=∞.相應地,環R的n-無撓弱整體維數w.T Fn.D(R)定義為sup{tfndRM|M是R-模}.

作為余撓模的深層次發展,文獻[8]在整環上引入War field-余撓模的概念.設R是整環,R-模U稱為War field-余撓模是指對任何無撓R-模D,都有文獻[9]證明了整環上每個撓的War field-余撓模,簡稱UT-模,內射維數不超過1.對非負整數n,本文在任意環上引入n-War field余撓模.R-模U稱為n-War field余撓模是指對任何n-無撓R-模D,恒有成立.顯然,0-War field余撓模就是內射模.由文獻[8,引理2.3]可知,整環上的無撓模是1-無撓模,從而整環上的War field余撓模就是1-War field余撓模.

下文中,對R-模M,其特征模HomZ(M,Q/Z)記為M+.現在來刻畫模的n-無撓維數.

定理2.2對R-模M及非負整數m,以下陳述等價

(1)tfndRM≤m;

(2)對任何R-模N∈Fn,

(3)對任何n-War field余撓R-模U,恒有成立.

進而,對任何n≥0,任何R-模M,恒有tfndRM≤n成立.從而,w.T Fn.D(R)≤n對任何環R都成立.

證 (2)?(1)?(3).顯然.

現在來刻畫環的w.T Fn.D(R)維數.

定理2.3對環R及非負整數m≤n,以下陳述等價

(1)w.T Fn.D(R)≤m;

(2)Fm=Fn;

(3)對R的任何理想I,tfndRR/I≤m成立.換言之,如果M是循環R-模,tfndRM≤m成立;

(4)對R的任何有限生成理想I,tfndRR/I≤m;

(5)如果M是有限生成R-模,tfndRM≤m成立;

(6)如果M是有限表現R-模,tfndRM≤m成立;

(7)如果U是n-War field余撓R-模,idRU≤m成立.

證由定理2.2可得(7)?(1)?(2),而(1)?(5)?(3)?(4)與(5)?(6)?(4)是顯然的.

(4)?(1)設m1=w.T Fn.D(R).則存在R-模M滿足tfndRM=m1,同時存在模N∈Fn滿足記s=fdRN.則m1≤s≤n.從而存在R的有限生成理想I滿足因此m≥tfndRR/I≥s≥m1.

(3)?(7)設I是R的理想.則由假設,tfndRR/I≤m成立.由定理2.2可得.因此idRU≤m.

現在借助w.T Fn.D(R),來刻畫FFD(R).

定理2.4對環R,以下各條等價

(1)FFD(R)≤n;

(2)w.T Fn+1.D(R)≤n;

(3)FFD(R)=w.T Fn.D(R).

證(1)?(2)設N∈Fn+1是任意R-模.由假設,fdRN≤n成立.因此由定理2.3可得w.T Fn+1.D(R)≤n.

(2)?(1)設N是R-模滿足fdRN=s<∞.不失一般性,可設s=n+1.則由定理2.3,fdRN≤n成立.從而FFD(R)≤n.

(3)?(1)運用定理2.3即可.

(1)?(3)設FFD(R)=k<∞.對任何模N∈Fn,則fdRN≤k.因此對任何R-模M,都有成立.故由定理2.3,w.T Fn.D(R)≤FFD(R)成立.現在仍設w.T Fn.D(R)=k,N是R-模滿足fdRN<∞.則由假設fdRN≤n成立.故對任何R-模M,由定理2.3可得因此fdRN≤k.從而FFD(R)≤k.

對R-模M,記滿足對任何有限表現模F,都有成立的最小非負整數n為FP-idRM.如果這樣的n不存在,則記FP-idRM=∞.一個凝聚環R稱為n-FC環是指FP-idRR≤n.由文獻[10,命題4.2.4],有

命題2.5設R是n-FC環,則FFD(R)=n.

推論2.6對環R,以下陳述等價

(1)FFD(R)≤1;

(2)2-無撓R-模的子模是2-無撓模;

(3)平坦R-模的子模是2-無撓模;

(4)對任何R-模N∈F2,都有fdRN≤1;

(5)R的每個(有限生成)理想I是2-無撓模.

推論2.7FFD(R)=0當且僅當F1=F0,當且僅當每個R-模是1-無撓模.

文獻[5,定理1&定理2]表明,對局部IF環或者chain IF環R,恒有FFD(R)=0.事實上,可以將這個結果推廣到任意IF環上.

命題2.8設R是IF環,則FFD(R)=0成立.因此一個IF環R或者是VN正則環,或者w.gl.dim(R)=∞.

證設M∈F1是任意R-模,且設0→F1→F0→M→0是正合列,這里F0,F1是平坦模.則也是正合的,且是內射模.由假設,R是IF環,故是平坦模.從而M+是平坦模.如此則M++也是平坦的.注意R是凝聚環,可由文獻[11]推出M是平坦模.從而由推論2.7有FFD(R)=0.

對于一個完全環R,由文獻[12]及文獻[13,定理2.2]可知,FFD(R)=0成立.但是滿足FFD(R)=0的環,卻未必是IF環,也未必是完全環.現在給出一個滿足FFD(R)=0,但它既不是完全環,也不是IF環的例子.

例2.9設xi是有理數域 Q 的未定元. 取T=Q[x1,···,xn,···],m=(x1,···,xn,···).則R1=T/m2是以m/m2為唯一極大理想的局部環.由于對任何,其零化子因此R1不是凝聚環,從而也就不是IF環.設R2是非Neother的IF環.則由文獻[6,定理3.2],R2不是完全環.構造環R=R1×R2.顯然,FFD(R)=0成立.但R既不是完全環,也不是IF環.

3 有窮平坦維數的換環定理

文獻[7]中稱R-模C是n-余撓模是指對任何R-模N∈Fn,都有.下文中,用Cn與T Fn分別表示n-余撓R-模簇與n-無撓R-模簇.現設A是一個R-模簇.其左,右正交類分別是A⊥={B|對所有A∈A,都有和⊥A={B|對所有A∈A,都有.對兩個R-模簇A和B,模簇對(A,B)稱為一個余撓理論,或者余撓對文獻[1]是指A⊥=B和A=⊥B同時滿足.文獻[14]表明(Fn,Cn)是余撓理論.

定理3.1對任意R-模M和N,存在正合列0→A→F→M→0與0→N→W→B→0,這里F,B∈Fn,A,W∈Cn.

證運用文獻[14,引理1.11&定理2.8]和文獻[15,引理2.1.1&引理2.1.2]即可.

對任何n≥1及任何環,總有T Fn?1.但一般情況下,卻未必有T Fn?1=T Fn.現在舉一個環的例子,滿足對任何n≥1,都有T Fn?1.

從而 cok(φ0πφ)cok(φ0), 且 fdRcok(φ0πφ)≤n. 設B是-模,且A是B的子模,滿足則由平坦維數的換環定理,有fdRB/A≤n.對任何同態f:A→Eu,考察如下交換圖

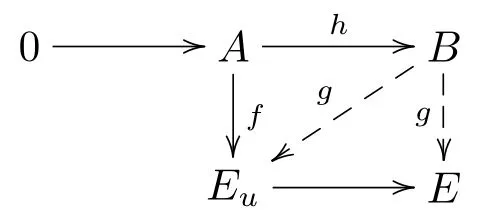
注意,E是n-余撓R-模,則存在同態g:B→E滿足f=gh.由于對任何x∈B,均有ux=0,則g(ux)=ug(x)=0且Im(g)?Eu.所以Eu是(n?1)-余撓-模.注意到則存在同態g:B→Eu滿足gφ0πφ=φ.因此gφ0π是同構,π是單同態.故A0=0,即C=Eu.從而由定理2.2,k:=tfndRA≥m+1成立.假如k>m+1,由上面的證明過程可知,存在n-余撓模E且fdRE≤n保證成立.這與的事實是矛盾的.這說明tfndRA=m+1.從而w.T Fn.D(R)≥m+1成立.

(2)記n=FFD(R).由定理2.4,w.T Fn+1.D(R)≤n成立.由(1),w.T Fn.成立.從而再由定理2.4可得

定理3.4設R是整環,則FFD(R)≤1當且僅當對每個非單位元06u∈R,都有FFD(R/(u))=0.

證設0是R的任何理想,記M=R/I.任取0,由于uM=0,則M是-模.記=R/(u).由假設,FFD(R/(u))=0成立.運用定理2.4,可得w.T F1.D(R/(u))=FFD(R/(u))=0.則也成立.由定理3.3,tf2dRM≤1.由定理2.3可得w.T F2.D(R)≤1.再次運用定理2.4,FFD(R)≤1成立.運用定理3.3,另一個方向是顯然的.

命題 3.5設x1,x2,···,xm是R上的未定元,這里m≥1.則FFD(R[x1,···,xm])=FFD(R)+m.

證只需證FFD(R[x1])=FFD(R)+1.設FFD(R)=s,N是R[x1]-模滿足fdR[x1]N≤s+2.考察文獻[2,引理9.29]中出現過的正合列0→N[x1]→N[x1]→N→0,有fdRN≤fdR[x1]N≤1+fdR[x1]N[x1]=1+fdRN,從而fdRN≤s+2<∞.因此fdR[x1]N≤s+1.則由定理2.3可得w.T Fs+2.D(R[x1])≤s+1.運用定理2.4,FFD(R[x1])≤s+1成立.另一方面,由于從而由定理3.3,成立.至此,有FFD(R[x1])=FFD(R)+1.

定理3.6設S是R的乘法封閉集.則FFD(RS)≤FFD(R).

證不失一般性,設m=FFD(R)<∞.設N是RS-模,且fdRSN<∞,從而fdRN=fdRSN<∞,有fdRSN≤m.從而有FFD(RS)≤m.

命題3.7設R是環,Max(R)(resp.Spec(R))是R的極大(resp.素)理想的集合.則FFD(R)=sup{FFD(Rm)|m∈Max(R)}=sup{FFD(Rp)|p∈Spec(R)}

證只需證FFD(R)=sup{FFD(Rm)|m∈Max(R)},另一個斷語類似可得.不失一般性,設t=FFD(R)<∞,s=sup{FFD(Rm)|m∈Max(R)}<∞.對任何m∈Max(R),由定理3.6,FFD(Rm)≤t成立.所以有s≤t.另一方面,設N是R-模滿足k=fdRN<∞.則存在正合列0→Fk→Fk?1→···→F1→F0→N→0,這里每個Fi是平坦模.對任何m∈Max(R),序列0→(Fk)m→(Fk?1)m→···→(F1)m→(F0)m→Nm→0是正合的,且每個(Fi)m是平坦Rm-模.則由假設,fdRmNm≤s成立.則fdRN=sup{fdRmNm|m∈Max(R)}≤s.故t=FFD(R)≤s.因此s=t,即FFD(R)=sup{FFD(Rm)|m∈Max(R)}.

4 凝聚環的有窮平坦維數

凝聚環R的弱整體維數w.gl.dim(R)一直備受學者們關注.本節中,將研究凝聚環的有窮平坦維數.

定義4.1R-模Q稱為n-投射模是指對任何內射維數不超過n的模H,都有

自然地,任何R-模都是0-投射模;投射R-模都是n-投射模,這里n≥1.

引理4.2(1)當n≥1時,每個n-投射模是n-無撓模;

(2)設R是凝聚環.當n≥1時,每個有限生成的n-無撓R-模是n-投射模.

證(1)設M是n-投射模,N是R-模且滿足fdRN≤n.則存在正合列0→Fn→Fn?1→···→F0→N→0,這里F0,···,Fn?1,Fn是平坦R-模.從而也是正合列,每個是內射模.從而idRN+≤n.由文獻[16,定理4.6.9],成立.從而.故M是n-無撓模.(2)設M是有限生成的n-無撓模,N是R-模且滿足idRN≤n.則存在正合列0→N→E0→···→En?1→En→0,這里每個Ei是內射R-模.從而也是正合列,且由文獻[10,定理2.2.13],每個是平坦模.從而fdRN+≤n.再由文獻[10,定理2.2.13],成立.從而故M是n-投射模.

為了刻畫FFD(R)≤2的凝聚環,先做如下定義.

定義4.3設M是R-模.M的n-投射維數m≥0,記為n-pdRM≤m,是指存在這樣的最小整數m,滿足序列0→Qm→Qm?1→Qm?2→···→Q0→M→0是正合列,這里每個Qi是n-投射模.如果這樣的m不存在,則記n-pdRM=∞.

引理4.4設R是凝聚環.對任何整數n≥1,都有

(1)若M是有限生成R-模,則n-pdRM=tfndRM;

(2)w.T Fn.D(R)=sup{n-pdRM|M是有限表現模}.

證(1)設tfndRM=k.從而有正合列0→Fk→Fk?1→···→F1→F0→M→0,其中F0,F1,···,Fk?1是有限生成投射模.注意Fk是M的第k?1個合沖.則Fk是n-無撓模.由于R是凝聚環,有Fk是有限表現的.因此由引理4.2,Fk是n-投射模.于是有n-pdRM≤tfndRM.再由引理4.2,n-pdRM≥tfndRM成立.故n-pdRM=tfndRM.

(2)由(1)即得.

定理4.5設R是凝聚環.對任何整數n≥0,以下等價

(1)FFD(R)≤n;(2)對每個有限生成R-模M,都有(n+1)-pdRM≤n;(3)對R的任何有限生成理想I,都有(n+1)-pdRR/I≤n.

證(1)?(2)由定理2.4和引理4.4即可得證.

(2)?(3)顯然.

(3)?(1)設I是R的有限生成理想.則R/I是有限表現模.由條件,(n+1)-pdRR/I≤n成立.運用引理4.4,tfn+1dRR/I=(n+1)-pdRR/I≤n成立.由此運用定理2.3可得w.T Fn+1.D(R)≤n.故由定理2.4,FFD(R)≤n成立.

命題4.6設R是凝聚環.對任何整數n≥0,都有

(1)如果FFD(R)=n,則對任何有限表現自反R-模M都有(n+1)-pdRM≤n?2;

(2)如果FFD(R)≤2,則任何有限生成自反R-模M都是3-投射模.

證(1)運用文獻[16,定理5.1.4],M?是有限表現的.設F1→F0→M?→0是正合列,其中F1,F0是有限生成自由模.考慮正合列,其中也是有限生成自由模,X是同態的上核.注意,X是也是有限表現模.由定理4.5可得(n+1)-pdRX≤n,有(n+1)-pdRM≤n?2.

(2)由(1)即得.

定理4.7設R是凝聚環,則以下各條等價

(1)FFD(R)≤2;(2)設M是有限表現R-模,則M?是有限生成3-投射模;(3)對投射模P的任意有限生成子模M,則tf3dRM≤1;(4)對R的任意有限生成理想I,則tf3dRI≤1.

證 (1)?(2)設M是有限表現R-模.則存在正合列F1→F0→M→0,這里F0,F1是有限生成自由R-模.則也是正合列,這里由條件,FFD(R)≤2成立,則由定理2.4可得w.T F3.D(R)≤2.故tf3dRC≤2.注意,均是有限生成投射模,故M?是3-無撓模.注意,R是凝聚環,從而M?是有限表現模.由引理4.2,M?是有限生成3-投射模.

(2)?(1)設M是任意R-模.則這里每個Mi是M的有限表現子模,對每個Mi,存在有限生成自由模Fi0,Fi1滿足序列是正合列.記Ki=ker(Fi1→Fi0).注意是正合列,這里從而C是有限表現模.由條件,C?是有限生成3-投射模.由文獻[17,引理3]可得K～=C?是有限生成3-投射模.故由引理4.4可得tf3dRMi=3-pdRMi≤2.故對任何R-模N滿足fdRN≤3,由定理2.2有再由定理2.2可得tf3dRM≤2.故w.T F3.D(R)≤2.則由定理2.4可得FFD(R)≤2.

(1)?(3)?(4)運用定理4.5和引理4.4即可.

正如人們把滿足w.gl.dim(R)≤1的凝聚環R稱為半遺傳環,在文獻[18]中把滿足G-w.gl.dim(R)≤1的凝聚環R稱為G-半遺傳環一樣,現在將滿足FFD(R)≤1的凝聚環R稱為 finitistic半遺傳環,并且遵循把半遺傳整環稱為Prfer整環,G-半遺傳整環稱為G-Prfer整環(見文獻[19])的習慣,也將 finitistic半遺傳整環稱為 finitistic Prfer整環.知道環R是半遺傳環當且僅當投射模的有限生成子模是投射模當且僅當R的每個有限生成理想是投射理想.自然地,要問,對于 finitistic半遺傳環,是否也有對應的表述？對此,有以下定理.

定理4.8對環R,以下陳述等價

(1)R是 finitistic半遺傳環;

(2)R的每個有限生成理想是有限表現的2-投射模;

(3)投射模的每個有限生成子模是有限表現的2-投射模;

(4)R是凝聚環,且平坦模的子模是2-無撓模;

(5)R是凝聚環,且對每個有限表現模M,都有2-pdRM≤1;

(6)R是凝聚環,且對每個有限表現模M,都有tf2dRM≤1.

證運用推論2.6可得(1)?(4),運用引理4.2可得(4)?(3),運用引理4.4可得(5)?(6),而(3)?(5)?(2)是顯然的.現只證(2)?(1).設I是R的任何有限生成理想.由假設,I是2-投射模,從而tf2dRR/I≤1.由定理2.3,w.T F2.D(R)≤1成立.再由定理2.4可得FFD(R)≤1.注意,由條件,I是有限表現的,故是凝聚環.從而R是 finitistic半遺傳環.

設R是交換環.稱R-模M是無撓模是指對x∈M及非零因子非單位a∈R,能由ax=0推出x=0.注意,平坦模是無撓模.眾所周知,整環R是Prfer整環(即w.gl.dim(R)≤1)當且僅當無撓R-模是平坦模.對于滿足FFD(R)≤1的整環R上的無撓模,有如下定理

定理4.9對整環R,以下陳述等價

(1)FFD(R)≤1;(2)如果A是無撓R-模滿足fdRA<∞,則A是平坦模;(3)如果A是無撓R-模滿足fdRA≤1,則A是平坦模.

證(1)?(2)記K=Q/R,這里Q是R的商域.由于A是無撓模,存在正合列這里每個KiK.由于B是平坦R-模且fdRA<∞,故fdRC<∞.由條件,FFD(R)≤1,故fdRC≤1.所以A是平坦模.

(2)?(3)顯然.

(3)?(1)設N是R-模滿足fdRN≤2.則存在正合列0→A→F→N→0,這里F是平坦模,且fdRA≤1.注意,A是無撓R-模.由條件,A是平坦模,即fdRN≤1.因此由推論2.6,FFD(R)≤1成立.

知道,整環R是Prfer整環當且僅當有限生成無撓R-模是投射模.對于finitistic Prfer整環,有如下定理.

定理4.10對凝聚整環R,以下陳述等價

(1)R是finitistic Prfer整環;(2)每個無撓R-模是2-無撓模;(3)每個有限生成無撓R-模是2-投射模.

證(1)?(2)設D是無撓R-模.則由文獻[8,引理2.3],D是1-無撓模.運用定理2.4與定理2.3可得D是2-無撓模.

(2)?(1)設I是R的理想.從而I是無撓R-模.由條件,I是2-無撓的.由推論2.6可得FFD(R)≤1.

(2)?(3)設M是有限生成無撓R-模,自然也是無撓模.由條件,M是2-無撓模.注意,R是凝聚整環,運用引理4.2,M是2-投射模.

(3)?(2)設M是無撓R-模.則,這里每個Mi是M的有限生成子模,自然也是無撓R-模.由條件,Mi是2-投射模.由引理4.2可知Mi是2-無撓模.故對任何R-模N滿足fdRN≤2,有故M是2-無撓模.

正如所有滿足w.gl.dim(R)≤1的環R不一定是凝聚環一樣,滿足FFD(R)≤1的環R也未必是凝聚環.

例4.11設C是復數域,X是C的未定元.構造環R=Q+XC[X].則由文獻文獻[20],文獻[21,命題3.2]及文獻[22,命題6]及文獻[23,定理4.11]可知FFD(R)≤1成立,但R不是凝聚環.

設R是整環,商域是K.設F(R)是R的所有非零分式理想的集合,f(R)是F(R)中所有有限生成元的集合.對任何06I∈F(R),其逆I?1定義為{x∈K|xI?R}.理想I∈f(R)稱為GV-理想是指I?1=R.記GV(R)={I∈f(R)|I是R的GV-理想}.在文獻[24]中,整環R稱為DW-整環是指GV(R)={R}.眾所周知,Prfer整環是DW-整環.

命題4.12設R是finitistic Prfer整環.則R是DW-整環.

證設0是R的有限生成真理想.取0,記T=R/(a).由定理3.4,FFD(T)=0成立.則I=J/(a)是T的有限生成真理想.記I=(b1,···,bn),這里b1,···,bn∈T. 如果 ann(I)=0,則同態映射f:T→Ts,f(r)=(b1r,···,bnr),r∈T是單射.從而序列是正合列,且cok(f)是有限表現模.注意,fdTcok(f)≤1且FFD(T)=0,則cok(f)是投射模,且則:T/I→Ts/ITs也是單射.由Im(f)?ITs可得到=0與I=T.顯然這是一個矛盾.因此ann(I)0.從而存在元素b∈R?(a)滿足I(b+(a))=0,故Jb?(a).則與成立.因此GV(R)={R},即R是DW-整環.

現在來研究滿足FFD(R)=0的整環.設R是整環.對內射R-模E,E自然是可除模,即對非單位元0,都有E=aE.從而乘法同態a:E→E是滿的,且序列是正合列.確切地,乘法同態a是同構當且僅當E是a-無撓的.

定理4.13對整環R,以下陳述等價

(1)R是域;(2)每個War field余撓模是內射模;(3)每個UT模是內射模;(4)FFD(R)=0.

證(1)?(4)與(2)?(3)是顯然的.在定理2.4中取n=0可得(4)?(2).現證(3)?(1).假如R不是域.則存在撓的內射R-模0.從而也存在非單位元06a∈R滿足E不是a-無撓的.則Ea0.由如下行是正合列的交換圖

可得EaHomR(R/(a),E).設X是任何無撓R-模.取正合列0→A→P→X→0,這里P是投射模.注意,fdRR/(a)≤1成立,則由文獻[8,引理2.3]可得正合列從而序列0→HomR(X/aX,E)～=HomR(X,Ea)→HomR(P/aP,E)～=HomR(P,Ea)→HomR(A/aA,E)～=HomR(A,Ea)→0是正合列.故由正合列可得.因此Ea是War field-余撓模.從而Ea是UT-模.由條件,Ea是內射模.另一方面,由于aEa=0,可得Ea不是a-可除的.故Ea不是可除模,自然也不是內射模.這顯然是個矛盾.故R是域.

試舉幾個例子來結束本文.首先,凝聚環R也未必有FFD(R)≤1.

例4.14構造環R=Z[x],這里Z是整數集,x是Z上的未定元.顯然,R是凝聚環.如果FFD(R)≤1,則由定理3.4可得FFD(R/xR)=0.而Z.故由定理4.13可知Z是域.這顯然是個矛盾.所以FFD(R)>1.

雖然對所有環R,均有FFD(R)≤w.gl.dim(R).但一般情況下,FFD(R)=w.gl.dim(R)未必成立.

例4.15設D是Prfer整環,其商域是L,F是L的擴域滿足[F:L]=∞.設是F上的形式冪級數環,且設構造如下兩個Milnor方圖

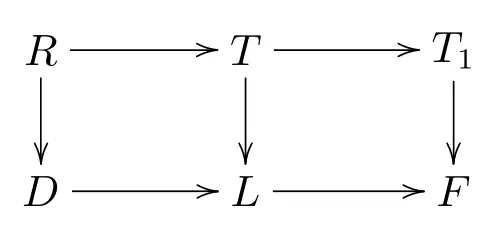
環R滿足FFD(R)<∞.卻未必有w.gl.dim(R)<∞.

例4.16設C(X,Y)是多項式環C[X,Y]的商域,Z是C(X,Y)上的未定元.取其極大理想m=(Z).構造環R1=C[X,Y]+ZC(X,Y)[Z]m.再構造環R2=Z4,這里Z是整數環.則R2是完全環,且w.gl.dim(R2)=∞.構造環R=R1×R2.則FFD(R)=2成立.由文獻[13,例4.6],w.gl.dim(R)=∞.

即使環R有w.gl.dim(R)=∞,也未必有FFD(R)<∞.

例4.17設,這里x是有理數域Q上的未定元,m=(x)是Q[x]的極大理想.則FFD(R)=1成立.設T=R[y1,y2,···],這里y1,y2,···是R上的未定元.由命題3.5,FFD(T)=∞.自然也有w.gl.dim(T)=∞.