考慮碳排放的煤炭鐵海聯運路徑優化

陳紅梅,宋浩賢,田 然

（燕山大學，河北 秦皇島 066000）

1 引言

隨著環境污染的日益加劇和可持續發展的要求，全球對“低碳化”的關注度越來越高，許多國家已經開始對碳排放實施碳稅政策。作為碳排放大國，我國承諾到2020年單位國內生產總值二氧化碳排放量相比2005年降低40%-45%，“低碳化”已成為我國經濟發展的必然趨勢。作為我國重要的戰略能源，煤炭在運輸途中消耗能源的同時，也會產生大量的碳排放，因此，實現煤炭的“低碳化”運輸對發展低碳經濟具有重要意義。由于我國煤炭產地與消費地相距較遠，單一的運輸方式難以滿足最優化運輸的要求，因此需要多種運輸方式的組合（即多式聯運）。研究表明，鐵海聯運是最適合煤炭的運輸組織方式，較單一運輸方式，鐵海聯運最多可減少77.4%的碳排放和43.48%的燃油，大力發展鐵海聯運可以有效減少煤炭運輸中的碳排放，緩解煤炭物流對環境的污染[1]。

國內外學者對多式聯運進行了富有成效的研究。Wang等建立考慮物流資源計劃（LRP）和多模態的多式聯運路徑優化模型，并通過GAMS軟件和CPLEX求解器求解[2]。Saeed等綜合考慮了多式聯運節點選址和路徑優化問題，以成本最小建立優化模型，并設計相應的遺傳算法求解，該算法能有效解決GAMS和CPLEX求解器無法在合理時間內找到最優解的問題[3]。Xiong等基于圖論建立了考慮運輸時間和成本的多式聯運雙層路徑尋優模型，并設計了相應的多目標Taguchi算法來尋找帕累托最優解[4]。生鮮貨物較一般貨物具有較強的特殊性，對運輸的要求也更高，Pawel等從貨物安全最大化和運輸成本最小化角度研究了易腐生鮮商品的運輸路徑優化問題[5]。考慮到多式聯運中的擁塞效應，Sushil等建立了考慮擁塞效應的兩階段路徑規劃模型，通過嵌套分解算法和PH算法求解[6]。在考慮碳排放的多式聯運中，Cecília等建立了考慮碳排放的多模態單程TRIPS優化模型，并采用經典的標量化方法進行求解[7]。Lam等通過建立以運輸成本和時間為目標、碳排放為約束的優化模型，研究了碳排放約束下的多式聯運路徑優化問題[8]。Gocmen等建立了考慮社會風險和生態風險的路徑優化模型，設計改進后的模糊算法對模型求解[9]。在煤炭鐵海聯運的研究中，蔡文結合我國煤炭調運實際情況與鐵海聯運特征，建立了基于成本最小的煤炭調運模型，并通過Lingo軟件進行求解[10]。田懷秀通過構建多商品流模型研究了鐵海聯運下的煤炭路徑優化問題[11]。

現有研究多從運輸時間、成本等方面考慮多式聯運路徑優化問題[12-16]，較少考慮碳排放因素，一些學者雖然將碳排放加入優化目標中，但多為建立多目標優化模型，將碳排放作為其中一個優化目標，未能有效評估碳排放的經濟成本[17-18]。此外當前研究多集中于集裝箱領域，關于煤炭等大宗散貨的研究相對較少。因此，本文通過引入碳稅機制，構建以運輸成本和碳排放成本最小為目標的鐵海聯運路徑優化模型，研究了碳稅機制下的煤炭鐵海聯運路徑優化問題。

2 問題描述與建模

2.1 問題描述

煤炭鐵海聯運過程如下：供應商根據客戶需求，委托鐵海聯運經營人將煤炭由產地發運至需求地，期間首先將礦區生產的煤炭匯聚到集貨點集貨，然后通過鐵路將煤炭運送至下水港，在下水港中轉換裝后由海運發運至上水港，上水后配送至客戶手中。在煤炭鐵海聯運網絡中，各運輸弧段與節點都存在運能約束。成本包括運輸成本和碳排放成本兩部分，其中運輸成本主要包括各運輸弧段的運輸費用、節點的中轉換裝費用、港口的作業費用以及堆場的堆存費用；碳排放成本為在征收交通運輸業碳稅的背景下，煤炭運輸途中和轉運時產生的碳排放所需繳納的碳稅金額。對鐵海聯運經營人而言，需要決策的問題是：如何安排運輸路徑，使得整個鐵海聯運網絡的總成本最小。

圖1 煤炭鐵海聯運概念圖

上述問題可歸類為網絡配流問題，不僅需要考慮運輸網絡的路徑規劃問題，還需要考慮運輸網絡中各線路的配流問題。針對上述問題，建立煤炭鐵海聯運路徑優化的多商品流模型，該模型將每一股不同的貨物流視為一種商品，根據多股貨物流在運輸網絡上的空間疊加特征進行建模，從而尋找最優的運輸路徑。

2.2 符號和變量

Nv：煤炭產地集合，v={1,2...,V}；

Nw：鐵路節點集合，w={1,2...,W}

Ns：港口節點集合，s={1,2...,S}；

Ne：煤炭消費地集合，e={1,2...,E}；

Pi：產地i的煤炭產能，i∈Nv；

Yj：消費地j的煤炭需求量，j∈Ne；

Qij：節點 i到 v通道的運能約束，i∈Nv?Nw,j∈Nw?Ns；

Qi：節點i的轉運能力約束，i∈Ns；

Cij：節點 i到 j的單位運輸成本（元/t·km），i∈Nv?Nw?Ns,j∈Nw?Ns?Ne；

Cs：港口單位中轉成本（元/t）；

Cp：港口單位堆存成本（元/t）；

Hi：港口最大煤炭吞吐量（t），i∈Ns；

T：煤炭在港平均堆存時間；

Cz：交通運輸業碳稅稅率（元/kg）；

dij：節點i到j運輸里程（km），i∈Nv?Nw?Ns,j∈Nw?Ns?Ne；

F1：鐵路運輸單位碳排放量（kg/t·km）；

F2：水路運輸單位碳排放量（kg/t·km）；

F3：港口中轉作業單位碳排放量（kg/t）；

（2）決策變量

xij：節點 i到 j的煤炭運量，i∈Nv?Nw?Ns,j∈Nw?Ns?Ne。

2.3 模型構建

2.3.1 模型假設

（1）交通運輸業所征收的單位碳稅是已知的。

（2）網絡中各運輸弧段運能不得超過能力限制，且各運輸弧段的運能均為已知。

（3）煤炭的中轉換裝只能發生在節點城市處。

（4）煤炭在節點處可拆分成多股分別運輸，將每一股不同的煤炭流視為一種不同的商品。

（5）在運輸過程中，煤炭質量不會增加或減少，不考慮隨機事件等因素的干擾。

（6）將上水港視為煤炭需求地，總成本中不考慮上水港作業費用。

2.3.2 模型建立

根據符號說明和模型假設建立考慮碳排放的鐵海聯運路徑優化模型：

式（1）由運輸成本和碳排放成本組成，表示整個網絡總成本Z最小；式（2）由節點間的運輸成本、中轉成本和堆存成本三部分構成，表示整個網絡的運輸成本；式（3）由節點間運輸、中轉產生的碳排放成本構成，表示整個目標網絡的碳排放成本；式（4）表示煤炭產地流量守恒約束；式（5）表示運輸至消費地的煤炭數量滿足需求；式（6）表示網絡中各節點間流量守恒約束；式（7）表示鐵路運輸通道運能約束；式（8）表示港口煤炭吞吐能力約束；式（9）為決策變量非負約束。

3 求解算法

遺傳算法采用遺傳機制不斷更新種群，具有較強的健壯性和全局搜索能力，但傳統遺傳算法的進化速度較慢，容易收斂到局部最優解，同時當問題復雜時，算法耗時較長。因此，在遺傳算法的基礎上引入精英保留策略，對算法進行改進，設計改進后的算法對模型求解，改進后算法求解步驟如下：

（1）染色體編碼。采用單層染色體自然數編碼方式，編碼時，用“0”（產地）作為染色體的頭部，如“0，2，6，8”，此染色體表示煤炭從產地0出發，依次經過節點2、6，最后到達需求地8。

（2）種群初始化。隨機產生個體數為N的種群P0，設定最大遺傳代數T，交叉概率Pr，變異概率Pm。

（3）適應度值評估。根據模型中的目標函數對種群中的染色體進行排序，得出其所屬的Pareto前沿等級。

（4）選擇操作。采用輪盤賭選擇策略，對于規模為n的群體P={a1,a2，…,an}，個體aj的適應度值為f(aj)，則其選擇概率為：

（5）交叉、變異操作。交叉采用正態分布策略，變異采用改進的自適應調整變異方式。

圖2 染色體交叉變異示意圖

（6）精英保留策略。在進化過程中，把每代的優秀個體保留下來作為下一代的父代，降低計算復雜度，加快算法的全局收斂速度，同時保證精英個體不被遺漏。

（7）終止條件。若運行代數達到最大遺傳代數T時，終止運行，否則轉到步驟（3）。

（8）得到目標函數的Pareto最優解集。

改進后的遺傳算法流程如圖3所示。

4 算例分析

4.1 背景設計

圖3 改進后的遺傳算法流程

以鄂爾多斯煤炭調運為例進行分析，2018年鄂爾多斯市煤炭產量為6.16億t，居全國第一位。假設鄂爾多斯市每年有3.5億t煤炭需要通過鐵海聯運運輸至廣州、上海、寧波、福州，四地煤炭需求量分別為1億t、1億t、1億t、0.5億t。下水港為北方煤炭港口中的秦皇島港、唐山港、天津港和黃驊港。運輸網絡如圖4所示，要求在該運輸網絡內，選擇最優的運輸路徑。為方便對各節點進行編號：鄂爾多斯為A1；準格爾、神木、呼和浩特、大同、朔州、集寧和遷安依次為B1-B7；秦皇島港、唐山港、天津港、黃驊港依次為C1-C4；廣州、上海、寧波、福州依次為D1-D4。

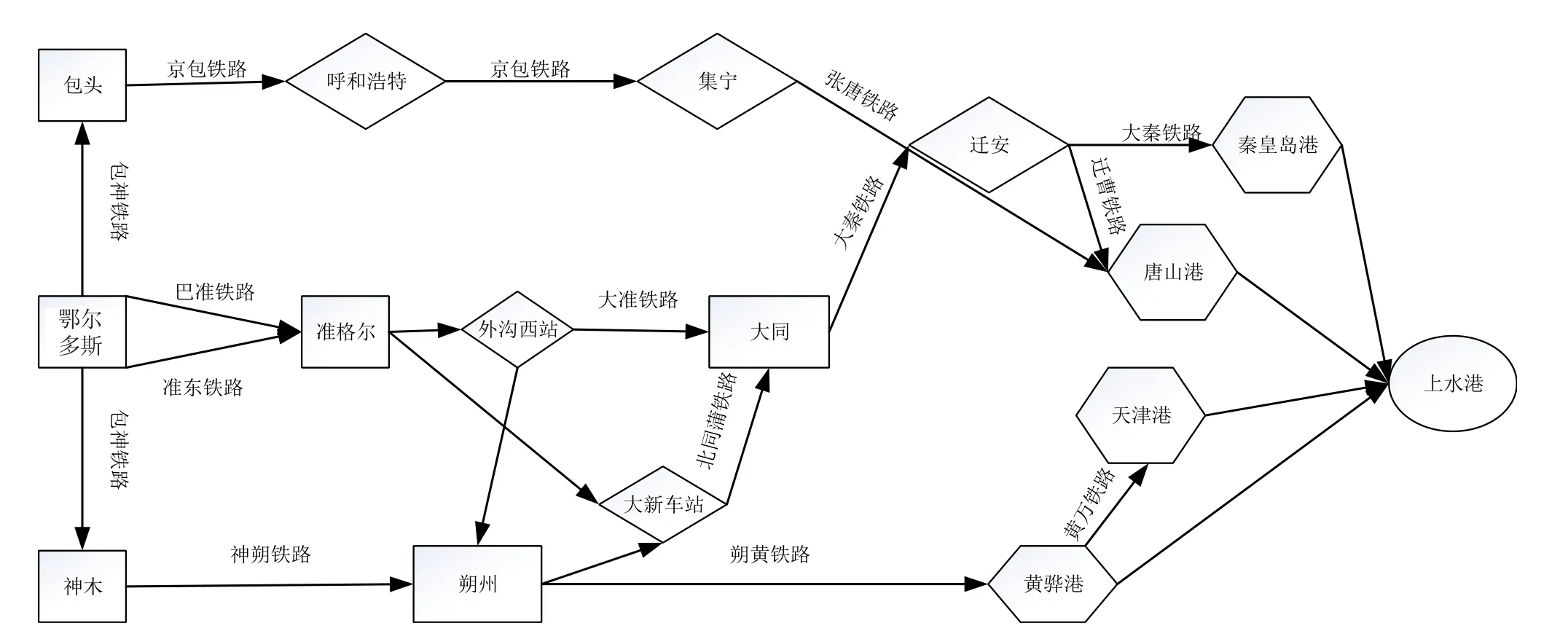
圖4 鄂爾多斯煤炭鐵海聯運網絡圖

鐵路運輸通道運距及運能見表1。由于鐵路煤炭運費計價方式不盡相同，為了方便研究，本文選取國鐵煤炭運費計價進行分析。國鐵整車煤炭運輸費用由基價1、基價2和鐵路建設基金組成，其中基價1為16.3元/t，基價2為0.098元/t·km，鐵路建設基金為0.033元/t·km，國鐵煤炭運價計算公式為Ct=TJ+J1*d+J2*d，TJ—基價1(元/t)；J1—基價2(元/t)；J2—鐵路建設基金(元/t·km)。

參考秦皇島港、唐山港、黃驊港和天津港煤炭年設計通過能力與近年吞吐量數據，本文假設津冀四港煤炭最大年吞吐能力為：秦皇島港2億t、唐山港3億t，天津港1億t，黃驊港2億t。由于海運價格受季節波動較大，且隨船型和距離不同而存在差異，因此本文將4-5萬DWT海運價格平均值作為各港口間的單位海運費用，港口間海運里程及單價見表2，該數據參考自中華航運網和中國煤炭信息網。我國北方煤炭港煤炭裝船費用為20-30元/t，煤炭的搬運、分揀等中轉費用約18-28元/t，因此設定煤炭中轉費用總和為50元/t。煤炭在港口內堆存時間取北方煤炭港口平均堆存時間，設定為6d，港口堆存費取0.2 元/(t·d）[19]。

征收碳稅已經被證明是最具成本效益的碳減排手段之一，目前部分國家已經開始征收碳稅，英國規定各行業每噸碳排放征收6.28英鎊；日本對消費化石燃料的企業，每噸碳排放征收655日元；荷蘭對一定經濟范圍內的企業每噸碳排放征收21歐元。結合國外碳稅征收情況與國內相關研究，假設我國未來征收碳稅成本Cz=0.1元/kg。設定煤炭鐵路運輸單位碳排放為0.022（kg/t·km)、水路運輸單位碳排放為0.016（kg/t·km）、鐵水中轉單位碳排放為4.28（kg/t）[11]。

4.2 結果分析

表1 運輸通道運距及通過能力

表2 海運里程及單價

采用MATLAB對該路徑進行模擬仿真。進行實驗的計算機配置為英特爾(R)酷睿(TM).i5-4210U2.7GHzCPU,2.0內存。設定種群規模為100，最大遺傳代數300，變異概率0.01，交叉概率0.9。

得到最優化的調運方案見表3。

即3.5億t煤炭拆分成五部分進行運輸，第一部分1.5億t煤炭經包神線由鄂爾多斯運輸至神木，再經神朔線運輸至朔州，由朔州運輸至黃驊港進行下水，最后1億t煤炭經水路發運至廣州，0.5億t煤炭經水路發運至寧波；第二部分1億t煤炭經巴準/準東線由鄂爾多斯運輸至準格爾，再經大準線運輸至大同，由大同經大秦線運輸至秦皇島港進行下水，0.7億t煤炭經水路發送至上海，0.3億t煤炭經水路發運至寧波；第三部分0.5億t煤炭經巴準/準東線由鄂爾多斯運輸至準格爾，再經準朔線運輸至朔州，由朔州運輸至黃驊港進行下水，最后經水路發運至寧波；第四部分0.2億t煤炭經巴準/準東線由鄂爾多斯運輸至準格爾，再經準朔線、北同蒲線中轉至大同，由大同運輸至秦皇島港進行下水，最后經水路發運至寧波；第五部分0.3億t煤炭經巴準/準東線由鄂爾多斯運輸至準格爾，再經呼準線、京包線運輸至集寧，由集寧運輸至唐山港進行下水，最后經水路發運至上海。最優化方案的目標函數值為843.05億元，運輸過程中碳排放總量為0.192 5億t。

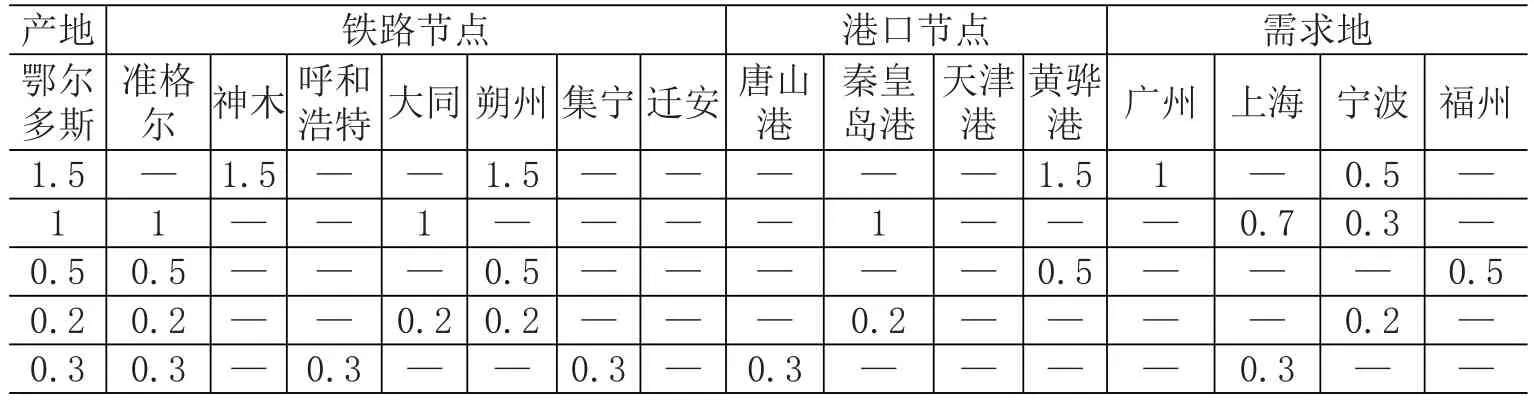
表3 煤炭調運優化計算結果 (億t）

5 結論

在國家大力倡導“低碳化”經濟發展的背景下，本文研究了考慮碳排放的煤炭鐵海聯運路徑優化問題。在結合煤炭鐵海聯運實際情況的基礎上，通過引入碳稅機制，構建了相應的路徑優化多商品流模型，使得在煤炭運輸過程中同時考慮運輸成本和碳排放成本，從而引導煤炭鐵海聯運經營人選擇碳排放水平較低的路線進行運輸。在求解算法方面，設計了一種帶精英策略的遺傳算法，通過引進精英策略，使得優良的種群個體在迭代過程得以保留下來，從而提高了優化結果的精度和算法求解速度。最后以鄂爾多斯地區煤炭調運為例驗證了模型和算法的有效性。

由于煤炭等能源類貨物較一般貨物具有較強的特殊性，在今后的研究中，需要進一步研究能源類貨物運輸中碳稅等參數的選擇，繼續探討碳稅成本對煤炭鐵海聯運路徑優化的影響，使得研究結果更加符合我國的實際國情。